3.2 Граничные условия для векторов электромагнитного поля (ЭМП)

До сих пор мы рассматривали среды с непрерывным изменением параметров ε, μ и σ, для которых справедливы все уравнения Максвелла в интегральной и дифференциальной формах. Вместе с тем, не во всех средах их параметры являются непрерывными функциями координат, часто встречаются скачкообразное изменение параметров среды, например на границах раздела разных материалов. При этом дифференциальные уравнения Максвелла на границах оказывается непригодным, так как производные в этих точках имеют разрыв. Поэтому уравнения должны быть дополнены граничными условиями, которые связывают векторы на границах сред.

граничные условия позволяют находить распределение электромагнитных полей на границах различных сред, таких как диэлектрики, проводники и вакуум. Это важно для расчетов в задачах электродинамики, оптики, и при проектировании антенн или устройств.

1. Смысл граничных условий

В уравнениях Максвелла фигурируют векторы и источники
электромагнитного поля. Но непосредственно в них не фигурируют
параметры среды. Следовательно, уравнения Максвелла
справедливы для сред с любыми параметрами и в том числе на
границе раздела различных сред. Однако на границе эти уравнения
принимают специальный вид — они формулируются в виде
граничных условий. Эти граничные условия мы далее и хотим получить.
Если среда однородна, то на воображаемой поверхности
внутри среды как нормальные так и тангенциальные составляющие
векторов поля будут меняться непрерывно при переходе через
эту поверхность.
Если же это граничная поверхность между двумя средами с
различными" электрическими параметрами, то заранее ниоткуда не
следует, что эти составляющие будут меняться непрерывно. Априори
неясно, какие составляющие векторов поля должны меняться
непрерывно, а какие составляющие могут терпеть скачок (разрыв
непрерывности).
Чтобы получить ответ на эти вопросы, мы воспользуемся тем
обстоятельством, что в действительности нет резкой границы между
двумя различными средами с различными электрическими параметрами.
Имеется некоторой толщины переходной слой, внутри
которого электрические параметры меняются непрерывно от их
значений в одной среде до их значений в другой среде. Поэтому
внутри слоя, как и вне его, справедливы уравнения Максвелла.
Резкую границу, а равно как и формулировку уравнений Максвелла
на границе, т. е. граничные условия, мы получим путем предельного
перехода.

2. Граничные условия для векторов D и B

Итак, пусть ось ох перпендикулярна переходному слою и пусть
ка рис. 1 кривая представляет собою изменение какого-нибудь
электрического параметра при переходе от среды I к среде I I .

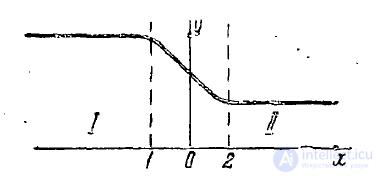
Рис. 1
Представим третье уравнение Максвелла в виде

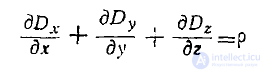
и проинтегрируем обе части этого уравнения в пределах от точки /до точки 2 (рис. 1).

Тогда получим

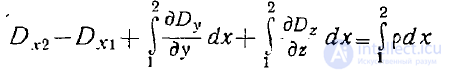
или, считая переходной слой достаточно тонким, найдем

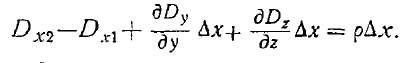
Производные 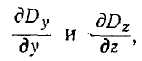- и поскольку они представляют собой изменения величин Dy и Dz в плоскости, параллельной граничной плоскости, должны быть конечными, поэтому при 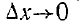получим где ps—поверхностная плотность зарядов, равная

причем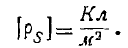
Видим, что уравнения Максвелла допускают существование поверхностных
зарядов и плотность их должна определяться формулой
(1).
Направив нормаль п к граничной плоскости по оси ох, можем
граничное условие для вектора D представить в виде

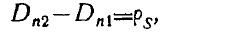(2).

если имеются поверхностные заряды и
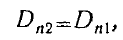, (3)
если на граничной поверхности таковых нет.
Нормальная составляющая вектора электрического смещения
при переходе через поверхность раздела двух сред терпит скачок,
равный поверхностной плотности зарядов, или меняется непрерывно,
если поверхностных зарядов нет.
Совершенно аналогичным образом можем получить граничное
условие для вектора В:
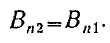(4)
Нормальная составляющая вектора магнитной индукции при
переходе через границу раздела двух сред меняется непрерывно.

3. Граничные условия для векторов H и Е

Пусть переходной слой такой, как показано на рис. 1. Представим
второе уравнение Максвелла в виде трех скалярных уравнений

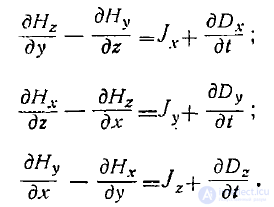
-Проинтегрируем последие .два уравнения в предела-х от точки
/ к точке 2 и получим

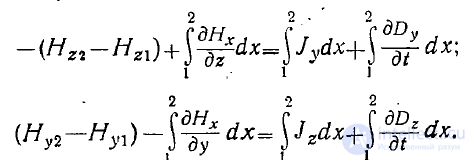
Считая переходной слой достаточно тонким, получаем

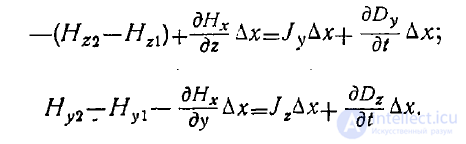
П р о и з в о д н ы е - 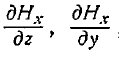-, поскольку они представляют собой

изменения величины #,. в плоскости, параллельной граничной пло-
dDy ÖD
скости, конечны, равно как и —^- и , поэтому при Дя-э-О получим
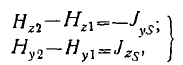(5)
где Jy = y°JyS 4- z°JzS— вектор поверхностной плотности T O K J P,
определяемый равенствами

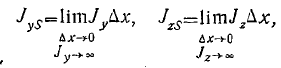x, (6)
причем [Jo] = 4 -
Дл^О их-*-О
J ѵ ~ » - э о У2-»-ао

Видим, что уравнения Максвелла допускают существование по
ъерхностных токов и плотность их должна определяться форму
лами (6).
Направив нормаль п к граничной плоскости по оси ох, из граничного
условия (5) получим
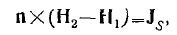, (7)
если имеются поверхностные токи, и

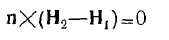
пли, взяв вектор t касательный к поверхности раздела,
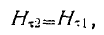(8)
если на граничной поверхности таковых нет.
Тангенциальная составляющая вектора напряженности магнитного
поля при переходе через поверхность раздела двух сред
іѵрпит скачок, равный поверхностной плотности токов, или меняется
непрерывно, если поверхностных токов нет.
Совершенно аналогичным образом можно получить граничное
условие для-вектора Е:
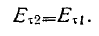. (9)
Тангенциальная составляющая вектора напряженности электрического
поля при -переходе через поверхность раздела двух сред
меняется непрерывно.
Внутри идеального -проводника ( з = о о ) , как следует из соотношений

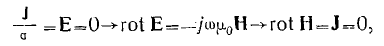
поле равно, нулю. Поскольку же соответствующие составляющие
поля при переходе через-поверхность идеального проводника терпят скачок, то должны появиться поверхностные заряды и токи,
так что 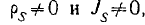, причем
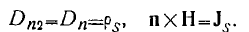(10)
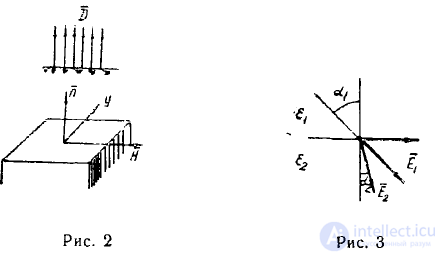
В этом случае тангенциальная составляющая электрического
поля и нормальная составляющая магнитной индукции равны нулю
(рис. 2).

3.1. Граничные условия для нормальных компонент векторов ЭМП

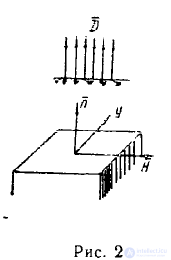
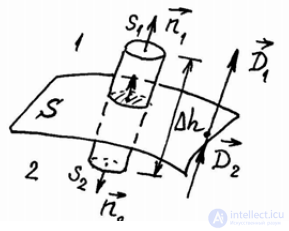
Рисунок 3.1

При рассмотрении граничных условий задача ставится следующим образом: пусть некоторая поверхность S разделяет две области пространства с параметрами ( ε1, μ1 и σ1) и (ε2 , μ2 , σ2 ). В окрестности
рассматриваемой точки поверхности выделим цилиндрический объем высотой Δh (рис.3.1), чтобы его ось
проходила по нормали к поверхности раздела сред, и рассмотрим потоки вектора индукции электрического
поля 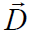через поверхность цилиндра.

.
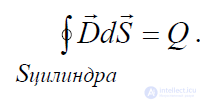
Выделим на поверхности цилиндра три характерные области: боковую
поверхность Sбок , а также основания S1 (верхнее) и S2 (нижнее). В соответ-
ствии с этим последнее равенство можно записать в виде:
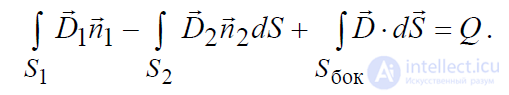. (3.1)
Будем полагать, что диаметр цилиндра настолько мал, что в пределах
обоих его оснований 1 S и 2 S индукцию электрического поля Dr
можно считать постоянной. Если устремить высоту цилиндра Δh к нулю ( Δh →0 ), то
интеграл по боковой поверхности в левой части последнего равенства также
устремится к нулю 0

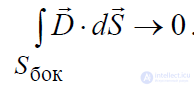
. Кроме того, при этом S1 и S2 будут неограниченно сближаться и в пределе сольются друг с другом, т.е.
S1 → S2 → S , а их векторы внешних нормалей будут соотноситься, как:

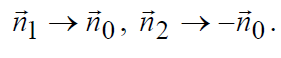
Учитывая сделанные допущения, уравнение (3.1) можно привести к следующему виду:

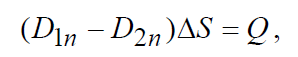
откуда следует:

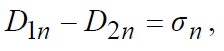(3.2)
где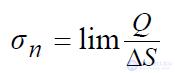
Если 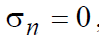, то
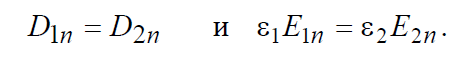. (3.3)

Аналогично из уравнения 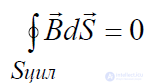находим

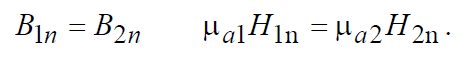. (3.4)

3.2 Граничные условия для тангенциальных компонент векторов ЭМП

Мы рассмотрели, как ведут себя нормальные компоненты векторов поля на границе раздела двух сред.

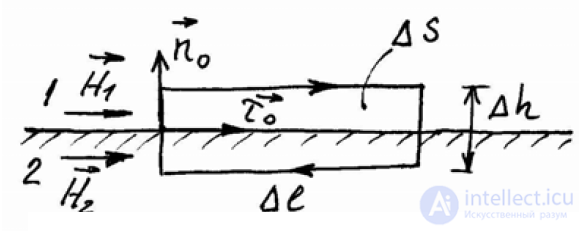
Рисунок 3.2

Теперь рассмотрим поведение тангенциальных компонент поля на границе раздела, для чего выделим контур L у поверхности раздела и рассмотрим циркуляцию вектора H
r
по выделенному
контуру. Запишем 1-е уравнение Максвелла в виде:

.
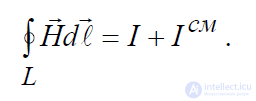
Будем полагать, что размеры контура L настолько малы, что в пределах
его напряженность магнитного поля H
r
можно считать постоянной. Тогда
левую часть этого уравнения можно раскрыть следующим образом:

.
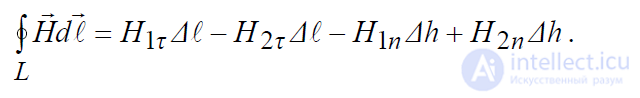
Теперь раскроем правую часть уравнения, для чего выразим ток проводимости I и ток смещения I см, пронизывающие поперечное сечение контура,
через их плотности. При этом можно выделить два случая:
- ток проводимости является объемным, тогда

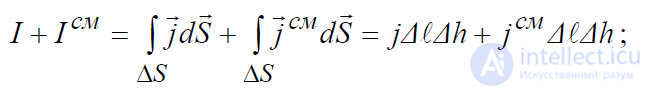
- ток проводимости течет по поверхности раздела двух сред (поверхностный ток)

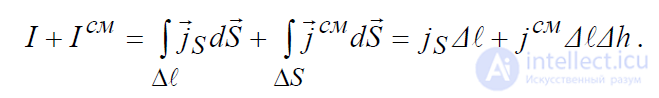
Приравнивая теперь левую и правую части уравнения, имеем:

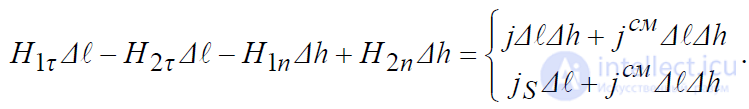
Переходя к пределу при Δh→0 , получаем
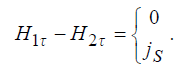. (3.4)
Аналогично, рассматривая циркуляцию напряженности электрического
поля E
r
по контуру L и применяя 2-е уравнение Максвелла, можно найти гра-
ничные условия для тангенциальных составляющих электрического поля:
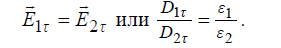. (3.5)
Более строго полную систему граничных условий можно записать в век-
торной форме:
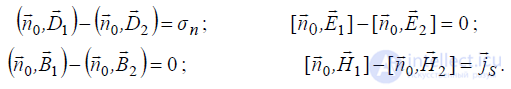(3.6)

3.3. Граничные условия на поверхности идеального проводника

Для переменных полей граничные условия на поверхности металлических тел существенно упрощаются, т. к. здесь принимается .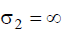

Поскольку плотность тока должна быть ограниченной величиной, то из 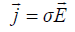следует, что E ≡ 0. Полагая во 2-м уравнении Максвелла E ≡ 0, получаем = 0
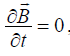поскольку поля переменные, то последнее равенство выполняется только при B ≡ 0 .

Таким образом, в идеально проводящей среде поля тождественно равны нулю (т. е. они внутрь среды не проникают). Если считать, что идеально проводящей является 2-я среда, то граничные условия записываются в виде

4. Преломление векторных линий электромагнитного поля на границе раздела сред

Согласно граничному условию (3) можем написать

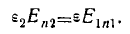
С учетом граничного условия (9)

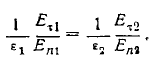
Обозначая

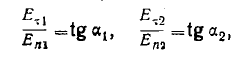
где 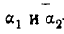—углы между линией, перпендикулярной к границе дела и векторами Е,і и Е2 в первой и второй средах (рис. 3),
лучаем
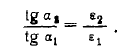(11 )
Аналогичным образом, используя граничные условия (4) и
находим
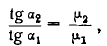(12)

где 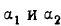— углы между линией, перпендикулярной к границе дела и векторами H1 и Н2 в первой и второй средах.

Если ту среду из двух граничащих сред считать электрически более «плотной», у которой е больше, то из формулы (11) следует, что электрические векторные линии поля при переходе из менее плотной в более плотную среду удаляются от перпендикуляра к границе раздела. Аналогичный вывод можно на основании формулы (12) сделать относительно магнитных векторных линий.

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.