1. Понятия ТЭП : Электрические заряды, ток проводимости, Силы в электрическом поле

Привет, Вы узнаете о том , что такое электрические заряды, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое электрические заряды, электрический ток проводимости, силы в электрическом поле , настоятельно рекомендую прочитать все из категории Теория электромагнитного поля.

1.1. электрические заряды

Опыт показывает, что при определенных воздействиях (например, трении) тела могут приобретать особые свойства – они способны электризоваться и взаимодействовать друг с другом. Мерой электризации в физике служит
электрический заряд q. Заряд q – это скалярная величина, которая в системе
СИ измеряется в Кулонах (Кл). Название единицы заряда увековечило имя
французского ученого Кулона, который открыл закон электрического взаимодействия заряженных тел.
В пространстве заряды могут быть распределены различными способами: дискретно либо непрерывно. Типичным примером
неделимого дискретного заряда может служить заряд электрона e= -1.6*10-19 Кл.

Иногда при теоретическом рассмотрении зарядов удобно использовать понятие
точечного заряда, под которым обычно понимается заряд произвольной величины, приписываемый телу с пренебрежимо малыми размерами (по сравнению с расстояниями, на которых рассматривается возбужденное им поле).
При непрерывном распределении заряда в объемном теле, удобно пользоваться понятием объемной плотности заряда, которая есть не что иное, как
заряд, приходящийся на единицу объема заряженного тела. Объемная плотность заряда является дифференциальной величиной и, в общем случае, определяется как предел:
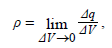, (1.1)
где ΔV – объем выделенного участка заряженного тела, Δq – заряд этого участка.
Если известна объемная плотность заряда как функция координат
ρ(x,y,z), то всегда можно найти полный заряд тока, как интеграл

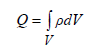. (1.2)
Иногда заряд распределяется не во всем объеме тела, а лишь на его поверхности. В этом случае в рассмотрение вводят поверхностную плотность
заряда (заряд единицы поверхности):
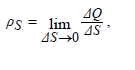, (1.3)

где ΔS – площадь выделенного участка заряженной поверхности, Δq – заряд
этого участка. Зная распределение ρs ее можно определить полный заряд
поверхности, как
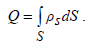(1.4)
Если имеют дело с заряженными протяженными объектами, например,
заряженной тонкой нитью, то вводят понятие линейной (или погонной) плотности заряда (заряд единицы длины):

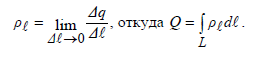(1.5)

1.2. электрический ток проводимости

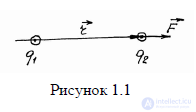
Рассмотрим некоторое тело с объемом V, имеющее
положительный электрический заряд Q. Пусть электрические заряды, по какой либо причине, вытекают из этого тела наружу через его поверхность S (рис.1.1).

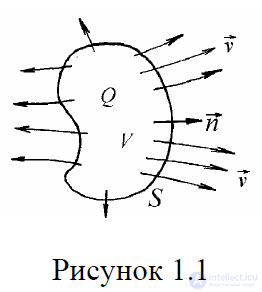
В этом
случае говорят, что через поверхность S течет электрический ток проводимости (или просто электрический
ток). В общем случае электрическим током проводимости называют процесс упорядоченного движения зарядов.
Величина (или сила) тока I, протекающая через поверхность S, численно
равна скорости изменения заряда в объеме V:
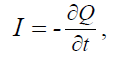, (1.6)
знак "минус" говорит здесь о том, что за положительное направление тока
принято направление движения положительных зарядов. Таким образом, си-
ла тока – это количество зарядов, прошедшее через определенное сечение
провода за 1 единицу времени. Единица измерения силы тока в системе СИ
есть 1 Ампер: A = Кл сек.
Движение зарядов графически удобно изображать с помощью линий то-
ка. Линии тока – это направленные линии, касательные к которым совпадают
по направлению с вектором скорости зарядов υ r в данной точке и в данный
момент времени. Можно себе представить, что соседние линии тока являются стенки некоторой трубки,
внутри которой течет ток. Эту воображаемую трубку
называют трубкой тока (рис.1.2).

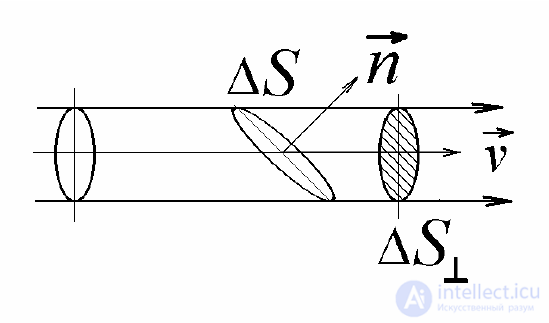
Рисунок 1.2

Если взять трубку
тока достаточно тонкой, то можно найти важную
дифференциальную характеристику тока, которая на-зывается объемной плотностью тока и определяется как
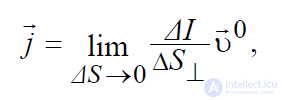, (1.7)
где ΔI – сила тока, текущего по выделенной трубке тока, ΔS⊥ – ее поперечное сечение, 0 υ r – единичный вектор скорости заряда, задающий направление
течения тока в данной точке. Об этом говорит сайт https://intellect.icu . В общем случае, если сечение ΔS расположено
под произвольным углом к линиям тока, то поперечное сечение ΔS⊥ можно
определить как скалярное произведение:

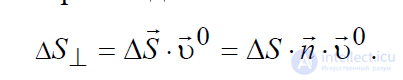(1.8)
Рассмотренный нами ток течет внутри всего объема тела, поэтому его можно
назвать объемным током. Весь ток I течет через сечение S, а величина тока,
бегущая через единицу поверхности называется
Если значение j
r
одинаково во всех точках сечения, через которое он течет, то говорят об однородном токе (или токе, равномерно распределенном
по сечению). Если j
r
по сечению неоднородно, то силу тока можно определить как поток вектора j
r
через поверхность S:

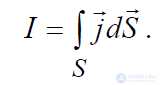(1.9)

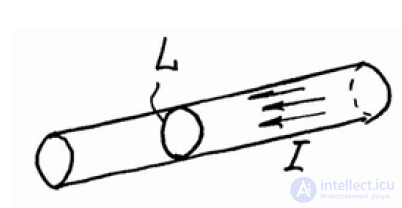
Рисунок 1.3

Иногда бывает случаи, когда ток течет не по всему объему тела, а лишь по его поверхности (рис.1.3),
тогда говорят о поверхностном токе и вводят понятие
поверхностной плотности тока
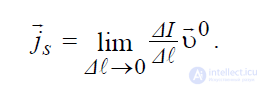. (1.10)
Полный ток выражается через его поверхностную плотность линейным
интегралом:
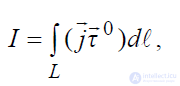, (1.11)
где L – периметр провода, 0 τ r – перпендикуляр к L на поверхности провода.

1.3. Силы, воздействующие на электрический заряд в электрическом поле. Векторы Er и Br электромагнитного поля

Экспериментально установлено, что электрические заряды оказывают
друг на друга силовое воздействие. Рассмотрим следующий пример. Пусть
имеется некий большой точечный заряд q1, расположенный в данной точке
пространства. Назовем этот заряд основным и поднесем к этому заряду другой точечный заряд, ничтожно малой величины, так называемый пробный
заряд qпр . На этот второй заряд, в какую бы точку пространства его не поместили, будет действовать сила F1r , "исходящая" из первого заряда. Эта сила
становится больше при приближении пробного заряда к основному, и меньше при увеличении расстояния r между зарядами. Следовательно, мы можем
утверждать, что в каждой точке рассматриваемого пространства существует
"нечто", что передает силу, исходящую от основного заряда, к пробному заряду. Это "нечто" присутствует и в том случае, если мы удалим из рассмотрения пробный заряд, и это объективно существующее "нечто" принято называть электрическим полем. Как известно, сила взаимодействия двух неподвижных точечных зарядов, согласно закону Кулона, пропорциональна величинам обеих зарядов:
, (1.12)
где ε – коэффициент, который называется диэлектрической проницаемостью
среды, 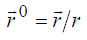единичный вектор, указывающий направление действия силы. В рассматриваемом примере пробный заряд, по сути, являлся своеобраз-
ным индикатором, позволяющий обнаружить электрическое поле основного
заряда. Чтобы получить характеристику этого поля, не зависящую от величины пробного заряда, силу F1
r
в (1.12) делят на qпр и полученную величину называют напряженностью электрического поля создаваемого основным
зарядом q1:

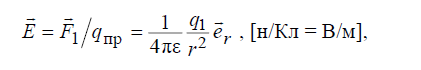(1.13)
Опыт показывает, что подобным свойством силового взаимодействия обладают и намагниченные тела, поэтому можно утверждать, что это взаимодействие передается также посредством некой объективно существующей
субстанции, которую называют магнитным полем. Кроме того, установлено,
что наличие магнитного поля можно обнаружить также и по его силовому
воздействию на движущийся электрический заряд qпр . Если известна скорость υ r , с которой движется заряд qпр , то это воздействие можно описать
силой Лоренца

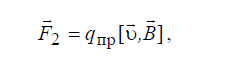(1.14)

которая позволяет ввести некоторую векторную величину B
r
, характеризую-
щую само магнитное поле:

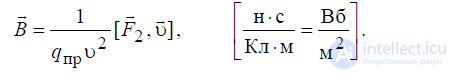(1.15)
Вектор B
r
называется вектором индукции магнитного поля. МодульB r
ра-
вен силе, которая действует на единичный электрический пробный заряд,
движущийся с единичной скоростью, а его направление перпендикулярно
этой силе и скорости движения.
Поскольку вектора Er
и Br
, характеризующие электрическое и магнитное
поля, зависят от точки приложения и могут изменяться со временем, то они в
общем случае являются функциями координат и времени. Эти функции
можно обозначить, как E(x, y, z, t)r
и B(x, y, z, t)r
. Если в некоторой области
пространства присутствуют оба поля, и электрическое, и магнитное, то можно говорить о наличии электромагнитного поля, которое воздействует на
пробный заряд с силой

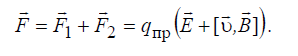(1.16)

1.4 Работа по перемещению заряда в электрическом поле. Электрическое напряжение. Электродвижущая сила

Из самого способа введения понятия напряженности электрического поля
следует, что это дифференциальная характеристика поля, поскольку характеризует его в каждой конкретной точке. Наряду с дифференциальными характеристиками поля силовые свойства поля могут быть описаны и интегральной характеристикой, тесно связанной с понятием работа. Найдем работу A, которую совершают электрические силы F
r
поля при перемещении точечно-
го заряда q из точки P1 в точку P2 :
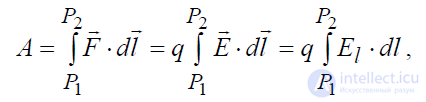(1.27)
где dl – элемент пути, по которому перемещается заряд из точки P1 в точку
P2.
Если отнести A к величине перемещаемого заряда, то получим интегральную характеристику поля, не зависящую от величины заряда:

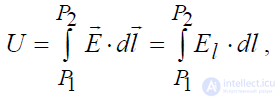, (1.28)
которая носит название напряжения между точками P1 и P2. Из определения следует, что напряжение между этими точками есть не что иное, как работа электрических сил по перемещению единичного заряда из одной точки в другую. Если заряд перемещается по замкнутому контуру L, то напряжение U называют электродвижущей силой, действующей в этом замкнутом контуре:

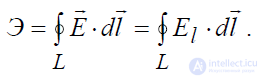(1.29)
Как видно из последнего соотношения, электродвижущая сила (или просто ЭДС) есть циркуляция вектора E
r
по контуру L. Эта интегральная характеристика очень часто используется при описании электромагнитных полей.

Исследование, описанное в статье про электрические заряды, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое электрические заряды, электрический ток проводимости, силы в электрическом поле и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория электромагнитного поля