18 Распространение плоских волн через многослойную среду кратко

Привет, Вы узнаете о том , что такое распространение плоских волн через многослойную среду, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое распространение плоских волн через многослойную среду , настоятельно рекомендую прочитать все из категории Теория электромагнитного поля.

1. Постановка задачи. Предполагаемый вид решения

Пусть на многослойную среду (рис. 1) падает плоская монохроматическая
волна. Требуется найти поле в любой точке любого
слоя. Поскольку каждый слои однородный,
т. е. в пределах каждого слоя л —
= const, то можно предположить, что поле
в каждом слое представляется в виде
суммы полей двух плоских волн — прямой
и отраженной.
Очевидно, что при этом любую составляющую
любого вектора электромагнитного
поля можно представить в виде
иЧ£/|еЛш'-*о'"'>,
где г — расстояние, отсчитываемое по направлению распространения
плоской волны.
Но это расстояние, 'как было показано на прошлой лекции, можно
записать так:
Z
пл
Пг
Рис.
t х
1
где
r=xs\n (p+ZCOS <р.
Используя эту запись, будем иметь
и=£/(z)e-'(ü''-~A'°л"s',1 f\
U(z)=\U\e-JK»zncos (1)
(2)

Мы хотим сконструировать решение задачи из плоских волн,
составляющие векторов которых имеют вид (1) и (2). Неизвестными
в этих выражениях являются постоянные амплитуда волны
\U\ и угол <р ее падения на границу слоя.
Очевидно, что мы должны различать здесь два вида поляризац
и и— горизонтальную и вертикальную. Для краткости горизонтально
поляризованную волну будем называть Г£-волной, а вертикально
поляризованную—ГМ-волной. Итак, будем предполагать,
что искомые составляющие векторов поля таковы:
ГЯ-волна 77И-волна
Е=Еу=иЕ(г)е^ШІ~к^"аіп^; H=/Уy=U' и(г)еНш'-"°хп%',п^\
Нх= \yH(z)e>{-mt-l<»x"sin^\ Еѵ= — V Е(г.)е№-к°хпзіГІ,*\
Hz=WH(z)e^""~K-Y"tin^; Ez=—\VE{z)e^l~^xn^ (3)
Ех=Ег=0, Hy=0. Hx=Hg*=0, Ey=Q.

2. Об этом говорит сайт https://intellect.icu . Аналогия с процессом в длинных линиях

Подставим в уравнения Максвелла
rot Е=—ДоцвН;
rot Н=/ше0Е
выражения (3), предварительно записав эти уравнения в скалярной
форме:
ГЕ-волна ТѴИ-волна
дЕ • дЕх дЕ, . и
дЕ . г, дН . г,
—=-1щаНг; -^=-jwzaEx;
дНх дНг . дН . -
IF ~ -Ыс еГ =l™*Ez-
Отсюда следует: ~;
dUF , dVE
-^~ІЩ^н\ - -%г -JK0nsin m «yzsin

— +jK0nsm ? WH=jwznUE. WE= "m, 4 UH.

Окончательно получаем систему уравнений
dz га ' dz
dVH dVE
- y =/u)ea c o s 2 < p £ / £ ; -fi- ~JM\iaCOS2 Сопоставим эти две системы уравнений с телеграфными уравнениями:
dU . . ,
Известно, что решением этой системы являются волны напряжения
U и тока / вдоль линии, причем коэффициент фазы равен
волновое сопротивление
* . - ) / £ • '
а решением системы будут выражения
У(С)=£ / ясс« ß C + / / , , Z e s i n ß : ;
/ ( : ) = / - ^ s i n ß ; + / K c o s ^ ; ,
где
£Ло — напряжение и ток в конце линии;
С— координата, отсчитываемая от конца линии:
Результаты сопоставления приведены ниже:
Г£ - в о л н а ТѴИ-волна
иЕ--и, UH-+I,
Ѵн-+І, VE-+U,
/
Ь 1 Z. - л f Ѵ-о _ _
" ^ с - Б І ^ - с - Б І ^ » * ' V ^os9=ZBcos^ZeH,
UE((,) = UEKCOS ßC-нѴя« . W ) = V£„cos p C + ; t / w«Zecos l / „ ( Q = / ^ c o s «psinßC+VWosßC, c 7 w ( C ) = / - ^ - s l n p C + c / w „ c o s ß C (4)

(С— координата, отсчитываемая от конца слоя).
K0 r t C O S

3. Элементарные сведения из теории матриц. Характеристическая матрица слоистой среды

Для конструирования решения задачи из приведенных, выше
формул удобно пользоваться матричным исчислением. В связи с
этим напомним элементарные правила матричного исчисления.
Квадратная матрица /ьго порядка записывается так:
'ап а12...а1п
I І = А.
і<з„, а „о ...а„
Произведением матриц А и В называется матрица, элементы c,-j
которой равны
л
с , 7 = ~2iaiKbKJ.
Матрица может состоять из одного столбца, например матрица-
столбец
w-(üb
Произведением квадратной матрицы А и матрицы-столбца Она
зывают матрицу-столбец Р, элементы которого равны
п
Рі = HjUIhCJk.
Л = 1
При внимательном взгляде на выражения (4) обнаруживаем,
что в случае Г-Е-волны эти выражения представляют собой матрицу
столбец
полученную в результате перемножения квадратной матрицы
j - ^ - sin ßC
, COS* , nr
/ -

на матрицу столбец
т. е.
CMQ=M£ ( C ) Q f , .
Аналогично, как нетрудно заметить, что для ТѴИ-волны
0я(С)=Мя(С)0ял-,
(6)
(7)
где
jZgCOS cpsin [К
cos ߣ
с / я ,
(8)
Матрицы (5) и (8) называются характеристическими матрицами
слоистой среды.
Заметим, что определитель обеих матриц равен единице.

4. Решение задачи

Мы установили полную аналогию задачи о распространении
электромагнитных волн в многослойной среде с задачей о распространении
волн напряжения и тока в последовательно соединенной
цепи отрезков длинных линий. Для того чтобы вычислить напряжение
и ток в некотором отрезке этой цепи, достаточно знать параметры
этого отрезка линии и нагрузку на ее конце. В рассматриваемой
задаче ситуация вполне аналогична. Для того, чтобы вычислить
поле внутри некоторого слоя, нужно знать, применяя терминологию
теории матриц, характеристическую матрицу данного слоя,
и матрицу-столбец амплитуд составляющих поля.
Характеристическую матрицу каждого слоя можно вычислить по
значениям коэффициентов преломления в каждом слое, используя
для этого закон Снеллиуса.
Итак, пусть требуется определить поле внутри первого слоя
(рис. 1). Согласно формуле (6) или (7) можем написать

Допустим, что нам известна матрица Q на границе ІѴ-го слря,
тогда согласно (9) можно написать

03)

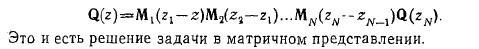
Исследование, описанное в статье про распространение плоских волн через многослойную среду, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое распространение плоских волн через многослойную среду и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория электромагнитного поля