Лекция
Привет, Вы узнаете о том , что такое электромагнитные свойства сред, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое электромагнитные свойства сред, классификация сред , настоятельно рекомендую прочитать все из категории Теория электромагнитного поля.
Простейшей по своим электрическим свойствам средой является свободное пространство — вакуум. Для этой «среды» имеет место следующая связь между векторами
поля:
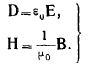. (I )
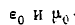— диэлектрическая и магнитная проницаемости свободного пространства, причем
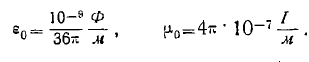
Свободное пространство характеризуется еще одним производным параметром:
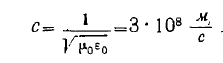— скорость распространения электромагнитных волн в свободном
пространстве.
Параметры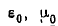 
— это все характеристики свободного пространства как среды.
Что касается других сред, то здесь мы имеем большое разнообразие соотношений между векторами поля, аналогичных (1) и значительно более сложных.
Эти соотношения называются материальными уравнениями.
Материальные уравнения представляют любой соотношения между самими векторами поля. Этим они отличаются от уравнений Максвелла, которые являются дифференциальными уравнениями.
Простейшие материальные уравнения для .реальных сред имеют, как уже было сказано, такой же вид, как н в случае свободного
пространства, т. е.
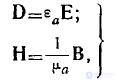(2)
где
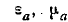—абсолютная диэлектрическая и магнитная проницаемости,
причем
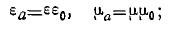
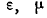— относительные диэлектрическая и магнитная проницаемости.
Существенно, что плотность тока J в уравнениях Максвелла может
играть двоякую, роль. Ток может быть источником поля,- то
есть причиной возникновения поля, но он может порождаться полем,
т. е. может являться следствием.
В последнем случае имеет место еще одно материальное уравнение
I, , Сименс Ом\ „
где а— проводимость среды I [а] = — — = — I . Это соотношение
представляет собой формулировку закона Ома в дифференциальной
форме. Параметры s, u-, а находятся либо экспериментально,
либо теоретически на основе модельных представлений о строении
вещества.
Материальные уравнения (2) связывают, между собой «силовые
» векторы Е и В и «количественные» векторы поля D и Н. Векторы
Б и В называются силовыми потому, что они, как видно из
выражения для силы Лорентца \
. F=<7(E+VXB),
определяют собой силу, действующую на заряд в электромагнитном
поле.
Векторы D и H называются количественными потому, что они
как видно из второго и третьего уравнений Максвелла в интегральной
форме, определяются непосредственно величинами зарядов и
токов, т. е. величинами, характеризующими источники электромагнитного
поля.
Ознакомившись с простейшими материальными уравнениями и
их смыслом, ниже рассмотрим классификацию сред по их электрическим
свойствам.
Векторы Er и Br полностью определяют электромагнитное поле в вакууме.
В случае же произвольной среды этих векторов недостаточно, т. к. они не учитывают свойства самой среды.
Поэтому вводят еще две векторные величины: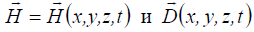 
, называя их напряженностью магнитного
поля и электрической индукцией (или электрическим смещением) соответственно.
Установим, как векторы Hr и Dr связаны с Er и Br.
Вначале рассмотрим действие электрического поля на вещество. При отсутствии внешнего поля
вещество является электрически нейтральным, т. е. там отрицательные и положительные заряды уравновешены.
Молекулы, из которых состоит вещество, могут быть полярные и неполярные.
В неполярных молекулах центр тяжести отрицательных зарядов совпадают с центром тяжести положительных, а в полярных молекулах эти центры не совпадают, так что молекулу можно рассматривать как диполь с дипольным моментом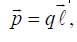 
, где lr вектор соединяющий заряды –q и +q.
С приложением внешнего поля Er к веществу полярные молекулы ориентируются вдоль его силовых линий.
Неполярные молекулы под действием электрического поля вначале поляризуются, а затем ведут себя так же, как полярные.
Этот процесс называется поляризацией вещества, для характеристики которого вводят вектор поляризации P
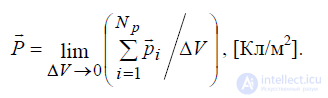(1.17)
где N p – количество упорядоченных электрических диполей в объеме
ΔV .
Величину поляризации Pr можно считать пропорциональной напряженности приложенного поля Er
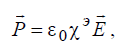(1.18)
где χэ – диэлектрическая восприимчивость среды, ε = 10−9 36π 0 [Ф/м] – универсальная электрическая константа.
Вектор электрической индукции определяют как
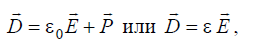, (1.19)
где .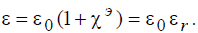 
Величина ε [Ф/м] называется абсолютной диэлектрической проницаемостью среды, а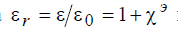 
называется ее относительной диэлектрической проницаемостью.
Вектор электрической индукции часто называют вектором электрического смещения, поскольку он учитывает смещение молекул в веществе при его поляризации.
Подобным же образом ведут себя вещества и во внешнем магнитном поле.
Атомы и молекулы многих из них могут быть уподоблены рамкам с током I, которые обладают магнитным моментом m ISn0 r r = .
В обычном состоянии рамки ориентированы хаотично, однако под действием внешнего магнитного поля Br они упорядочиваются, что приводит к намагничиванию материала.
Намагниченность среды характеризуется вектором
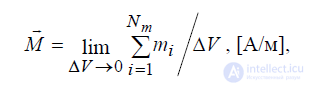(1.20)
где Nm – количество упорядоченных магнитных диполей в объеме ΔV .
Для учета влияния намагниченности среды вводят вектор напряженности
магнитного поля:
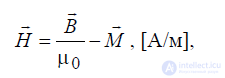, (1.21)
где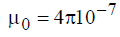 
− [Гн/м] – универсальная магнитная константа.
Векторы Mr и H r
считают пропорциональными друг другу (для линейной
среды):
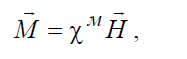
(1.22)
где χм – магнитная восприимчивость.
Из двух последних равенств следует
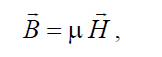, (1.23)
где (1 м )
μ = μ0 + χ – абсолютная магнитная проницаемость среды, а м
μr = μ μ0 = 1+ χ – относительная магнитная проницаемость.
Следует отметить, что векторы D
r
и H
r
при одинаковых внешних источ-
никах полей не зависят от среды, т. Об этом говорит сайт https://intellect.icu . е. не зависят от внутримолекулярных зарядов и токов вещества.
Параметры εa , μa , χэ и χм характеризуют свойства вещества, обусловленные связанными зарядами. Однако кроме связанных зарядов внутри вещества могут быть свободные заряды, которые начинают упорядоченное
движение при действии внешнего электрического поля, образуя ток проводимости. Плотность тока проводимости j
r
пропорциональна напряжению
электрического поля :
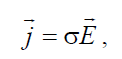
, (1.24)
где σ [1 (Ом⋅м) ] – удельная проводимость среды.
Последнее равенство выражает дифференциальную форму известного закона Ома для участка цепи.
Все среды характеризуются тремя параметрами: ε, μ и σ. В зависимости
от свойств параметров ε, μ и σ среды делятся на:
1) линейные и нелинейные: если хотя бы один из параметров среды ε, μ или σ зависит от величины приложенного поля E r или Hr , то среда считается нелинейной, если такой зависимости не наблюдается, то среды называются линейными;
2) однородные и неоднородные: если хотя бы один из параметров среды ε, μ или σ зависит от координат, то среда считается неоднородной, если такой зависимости не наблюдается, то среды называются однородными;
3) изотропные и анизотропные: если свойства среды одинаковы по трем ортогональным направлениям, то среда изотропная, если нет – то анизотропная. В изотропных средах ε, μ и σ – скалярные величины, а для
описания анизотропных сред они тензоры. Тензоры записываются в виде матрицы. Например, в декартовой системе координат они имеют вид:
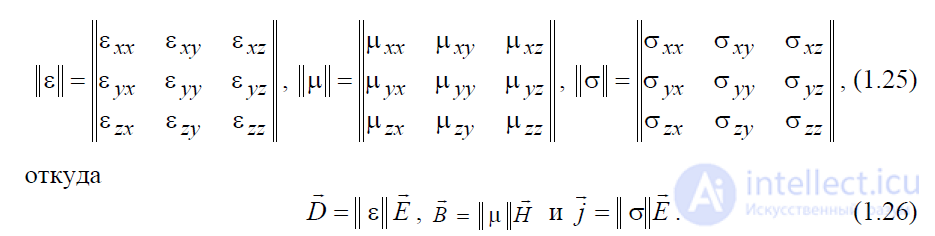
При этом векторы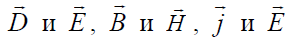 
в общем случае оказываются непараллельными.
Изотропными называются среды, у которых электрические свойства одинаковы по всем направлениям.
В этом случае в произвольно выбранной прямоугольной системе координат при произвольно направленном векторе Е имеют место равенства
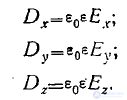
Следовательно, здесь как бы- ни был направлен вектор Е, будет
D=eneE
и аналогично
J = o £ ,
то е'сть, в изотропной среде вектор D коллинеарен Е, вектор В кол-
линеарен Н, вектор J коллинеарен Е.
Анизотропными называются среды, у которых электрические
свойства различны в разных направлениях. В этом случае в некоторой
прямоугольной системе координат может оказаться, что при
направлении вектора Е по осп ох, получим
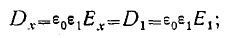; (За)
при направлении по оси оу
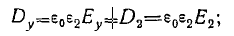; (3 6)
при направлении по оси oz
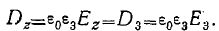(Зв)
Предположим, что вектор Е лежит в координатной плоскости
хоц той же системы координат и направлен под произвольным углом
к оси ох. В этом случае, раскладывая вектор В на составляющие'
1 по координатным осям, получим
И поскольку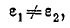 
, вектор
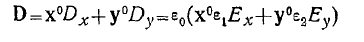
уже не будет коллинеарен вектору Е (рис. 1).
Однако соотношения (3) и последующие справедливы в исключительной
системе координат. В произвольной прямоугольной системе .координат соотношения между составляющими векторов D и Е для анизотропных сред более сложны:
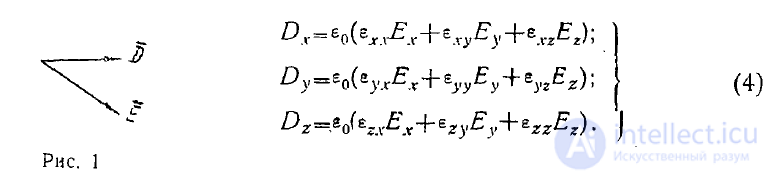
Девятка чисел в, виде матрицы •tj называется тензором.
Тензор записывается в
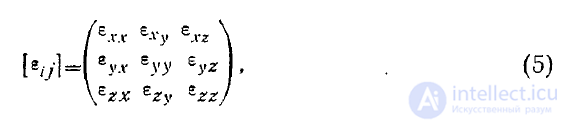
где
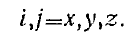
Тензор является обобщением скаляра и вектора.
Скаляр — величина, которая характеризуется одним числом, и для его описания не требуется никаких индексов.
Вектор — величина, которая характеризуется тремя числами (тремя координатными составляющими), и для его описания требуется один индекс (х или у или z).
Тензор—величина, которая характеризуется девяткой чисел, и для его описания требуется два индекса (хх или ху или yz и т. д . ) .
Соответственно скаляр-тензор нулевого ранга, вектор—тензор первого ранга, а тензор диэлектрической проницаемости — тензор второго ранга.
Тензорами могут являться и магнитная проницаемость [х и проводимость а.
Если хотя бы один из электрических параметров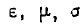 
является тензором, то среда анизотропна.
Примерами анизотропных сред являются кристаллы, ионосфераТензор диэлектрической проницаемости, как, впрочем, и тензоры \l, а как будет показано,— симметричный тензор, т. е.
Это означает, что тензор диэлектрической проницаемости в действительности характеризуется не 9, а лишь 6 различными числами.
Однородной называется среда, у которой электрические параметметры не зависят от координат.
Так, в случае изотропной среды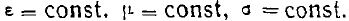 
.
В случае однородной анизотропной среды все составляющие тензоров электрических параметров не должны зависеть от координат.
Неоднородной называется среда, у которой электрические параметры зависят от координат или хотя бы один из параметров зависит хотя бы от одной координаты.
Примером неоднородной среды может служить атмосфера. Среды бывают линейные и нелинейные. Линейной называют среду, у которой электрические параметры не зависят от величин векторов электромагнитного поля. Нелинейной называют среду, у которой электрические параметры зависят от величин векторов электромагнитного поля. Примером такой среды может служить ферромагнетик, у которого магнитная проницаемость зависит от величины напряженности магнитного поля. В принципе все среды нелинейны, однако эта нелинейность проявляется при очень больших величинах векторов поля.
Среды, обладающие проводимостью, характеризуются еще производным параметром — временем релаксации. Получим этот параметр:
J=oE (полагаем a—const);
div J + 1 = 0 ;
d l v E = — (полагаем e=const).
Из этих трех соотношений находим
Решая это уравнение для фиксированной точки, находим •
t
где
Po — начальная плотность зарядов;
t = —время релаксации; оно показывает, как быстро растекается
скопление зарядов плотностью р0 в среде.
Например, для:
— меди о ~ 1 0 7 — , е=1,
т ~ 1 0 - 1 8 < : ;
— морской воды а=4 ^ , s=80,
х=2 - 1 0 - 1 0 с;
— с т е к л а o = 1 0 ~ 1 2 ^ < е=2;
т=20 с;
—кварца б = 1 0 - п Щ-, е=2,
х=2- 106 с ^ 2 5 суток.
Как видно из этих данных, в металле скопление зарядов почти
мгновенно растекается и оказывается на поверхности проводника.
Далее заключаем, что чем лучше изолятор, тем больше в,ремя релаксации.
В настоящем курсе лекции мы будем изучать теорию электромагнитного
поля применительно только к линейным средам. В этом
случае уравнения Максвелла линейны. Поэтому зависимость от
времени здесь удобно представлять при помощи временного множителя
е ы . Так что любая величина, характеризующая электромагнитное
поле, представляется в виде произведения функции координат
и указанного временного множителя. При этом функция,
зависящая от координат, может быть и комплексной. Значит
функции, зависящие от координат в теории электромагнитного поля,
могут одновременно быть и векторными, и комплексными. Например,
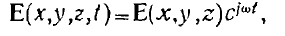
т. е. здесь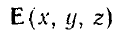 
— векторная комплексная функция координат:
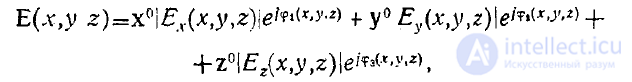
где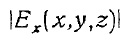 
. — модуль, а 
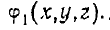..—аргумент или фзза комплексного числа 
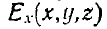и т. д.
Учитывая, что
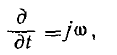
т. е. производная по времени есть оператор умножения на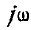 
, уравнения Максвелла запишем в виде
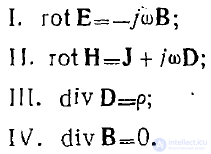
Полагая во втором уравнении
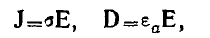
можем его представить в виде
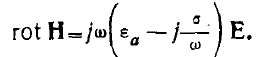
Сравнивая это уравнение с.уравнением в случае диэлектрика (а=0)
т. е. с уравнением
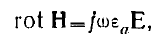, (7)
видим, что целесообразно ввести в рассмотрение комплексную диэлектрическую проницаемость
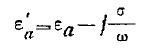
и написать
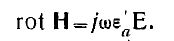(8)
Сравнивая уравнение (8) с уравнением (7), видим, что формально уравнения в случаях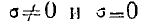 
не отличаются друг от друга.
Это обстоятельство, как увидим далее, приводит зачастую к значительным упрощениям.
Итак, диэлектрическая проницаемость, как впрочем и магнитная проницаемость, может быть комплексной величиной. В связи
с этим заметим, что тензор диэлектрической проницаемости в общем случае удовлетворяет условию
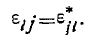(9)
(Звездочка означает комплексно сопряженное число).
Тензор, обладающий этим свойством, называется эрмитовым (по имени ученого Эрмита). Следовательно, симметричность тензора
(равенство (6)) вытекает из условия (9).
В радиотехнике параметры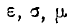 
многих сред почти не зависят от частоты.
Такая зависимость начинает сказываться лишь в самой коротковолновой части спектра радиоволн.
В оптическом диапазоне волн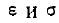 
зависят от частоты, т. е. имеет место дисперсия.
Исследование, описанное в статье про электромагнитные свойства сред, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое электромагнитные свойства сред, классификация сред и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория электромагнитного поля
Комментарии
Оставить комментарий
Теория электромагнитного поля
Термины: Теория электромагнитного поля