Лекция
Привет, Вы узнаете о том , что такое отражение, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое отражение, преломление , настоятельно рекомендую прочитать все из категории Теория электромагнитного поля.
Решение задачи об отражении и преломлении плоских волн на границе раздела двух сред находит широкое применение в теории распространения радиоволн и в оптике.
Пусть на границу раздела сред падает плоская волна. Возмущающее действие границы, как можно предположить, сведется к появлению отраженной и преломленной волн.
Любая плоская волна в отдельности является решением уравнений Максвелла. Однако для того, чтобы указанные волны представляли собой решение задачи, необходимо, чтобы они совместно с падающей
волной удовлетворяли граничным условиям на поверхности раздела сред.
Итак, пусть напряженность поля падающей волны
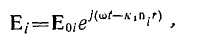
а напряженности полей отраженной и преломленной волн соответственно равны
где 
, (среды считаем диэлектриками).
Направления распространения будем характеризовать углами
( рис . 1 ) :
—угол падения; этот угол считаем известным;
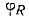и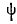 
— искомые углы отражения и преломления;
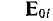— известно;
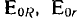— неизвестны.
Граничные условия, которым должны удовлетворять совместно все три волны,
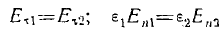(1)
либо
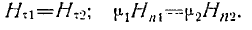(2)
В результате подстановки выражении для полей всех трех волн в какое-либо из граничных условий получим соотношение следующего вида:
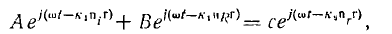
где r —радиус-вектор какой-либо точки граничной плоскости, проведенный из точки падения (рис. 2). Это равенство должно выполняться на всей граничной плоскости при любой величине вектора г. А это возможно тогда и только тогда, когда все три фазовых множителя равны, т. е. когда выполняются условия
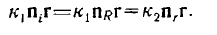
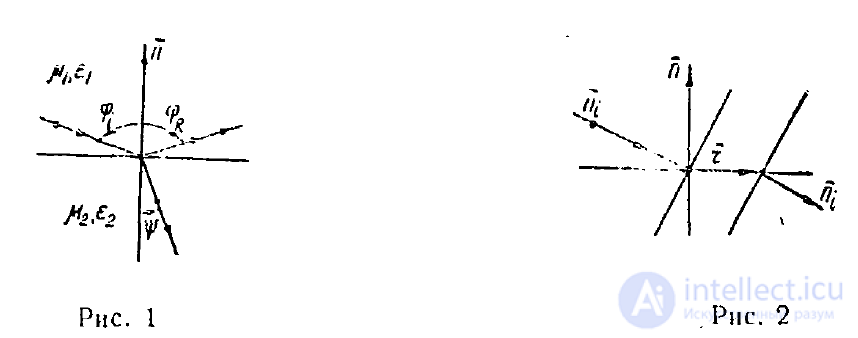
Рис. 1 Рис. 2
Выясним смысл этих двух равенств.
Для этого учтем тождество
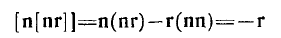(поскольку пг = 0 ),
и получим
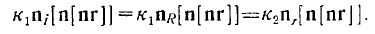
Произведем здесь циклическую перестановку векторов и придем к равенствам
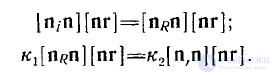
Поскольку эти равенства должны выполняться при любой величине вектора [пг], то должно быть
Эти два векторных равенства представляют собой формулировку законов отражения и преломления плоских волн.
1. Луч падающий, луч отраженный и луч преломленный лежат в одной и той ж е плоскости — плоскости падения.
Плоскость падения — это плоскость, в которой лежат вектор п, и вектор n — нормаль к границе раздела, восстановленная в точке падения.
2. 
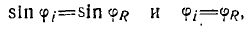угол отражения равен углу падения.
3. 
Эти законы справедливы при любой поляризации падающей волны.
В то же время коэффициенты отражения ц прохождения зависят от вида поляризации падающей волны.
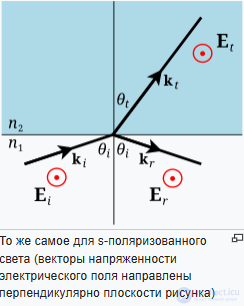
Характерными видами поляризации являются вертикальная и горизонтальная поляризации. При вертикальной поляризации вектор Еi лежит в плоскости падения, а при горизонтальной поляризации
в плоскости падения лежит вектор Нi- (рис. 3). Очевидно, что произвольный случай поляризации путем разложения вектора Еi на два составляющих вектора, лежащих соответственно в
плоскости падения и перпендикулярно ей, можно свести к этим двум случаям поляризации. ,
Используем граничные условия ( I ) (рис. 4):
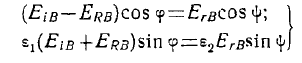(5)
Рис. 3 Рис. 4
(индекс «В» — вертикальная поляризация).
Вместо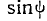 
из закона Снеллиуса во втором уравнении подставляем
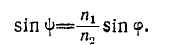
Затем решаем систему уравнении (5) относительно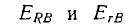 
и находим
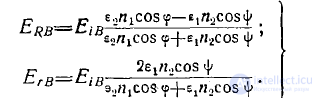(6)
При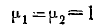 
эти формулы принимают вид
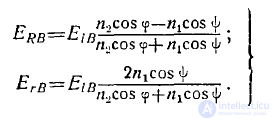(7)
В последних двух формулах можно с помощью закона Снеллиуса исключить n1 и n2 и получить
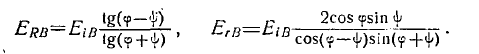(8)
tg( Соотношения (6) — (8) называют формулами Френеля.
Формулы Френеля справедливы в том случае, когда граница раздела двух сред гладкая, среды изотропны, угол отражения равняется углу падения, а угол преломления определяется законом Снеллиуса. В случае неровной поверхности, особенно когда характерные размеры неровностей одного порядка с длиной волны, большое значение имеет диффузное отражение света на поверхности.
В компьютерной графике lля аппроксимации вклада фактора Френеля в зеркальное отражение используется аппроксимация Шлика.
Для того чтобы найти формулы Френеля при горизонтальной поляризации, воспользуемся аналогией между граничными условиями для векторов Е и Н. Об этом говорит сайт https://intellect.icu . Как видно из (1) и (2), а также.рис. 3,
искомые формулы можно получить из формул (6), если параметры 6j и е2 заменить параметрами и ц2 , а Е-,в, ÉRB, ЕГВ сооіветственно 
(индекс „Г" — горизонтальная поляризация).
В результате получим
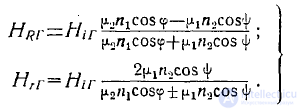(9)
Чаще всего оперируют вектором Е, и поэтому в формулах (9) целесообразно векторы H заменить векторами Е, для чего следует воспользоваться равенством
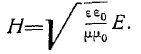
При этом в первой формуле (9) коэффициент при Е ; г останется без изменений, вторая же формула преобразуется к виду
При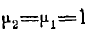 
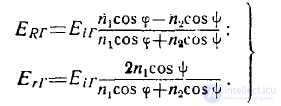(10)
В этих формулах с помощью закона Снеллиуса можно исключить n1 и n2 и получить
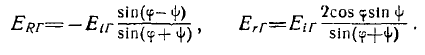(11)
Рассмотрим задачу о падении плоской ЭВМ на плоскую границу раздела, делящую все пространство на две части (рис.8.1). Пусть верхнее полупространство заполнено средой 1 с параметрами ε1, μ1, σ1, а нижнее – средой 2 с параметрами ε2, μ2 , σ2 .
Рисунок 8.1
Назовем плоскостью падения плоскость, проходящую через луч и нормаль к поверхности раздела.
Комплексные амплитуды напряженности электрического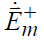 
и магнитного 
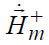полей падающей волны можно записать в следующем виде
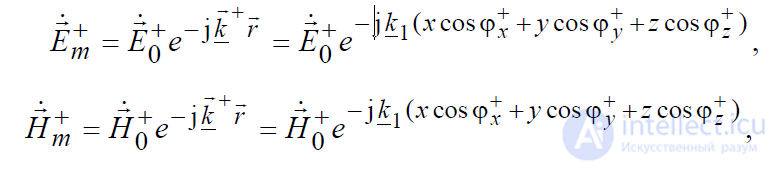
, (8.1)
при этом 
,
где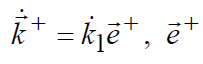 
– орт луча падающей волны, 
– направляющие косинусы вектора e + r в прямоугольной системе координат.
Естественно предположить, что векторы напряженности поля отраженной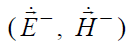 
и переломленной 
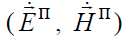волн также являются плоскими и выражаются аналогичными соотношениями:
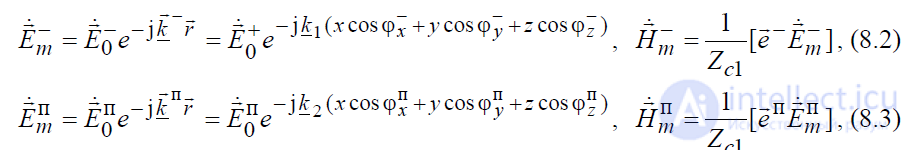
где −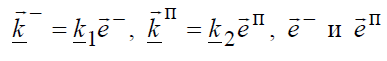 
– орты лучей отраженной и преломленной волн соответственно,
а 
– их направляющие косинусы.
Найдем направления лучей отраженной и преломленной волн, полагая, что направление луча падающей волны нам задано:
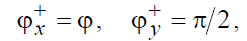
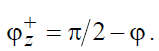
. Для этого используем граничные условия для тангенциальных компонент векторов 
на плоскости раздела ( x = 0 ) двух сред:
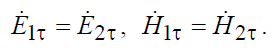. (8.4)
На основании граничных условий можно записать:
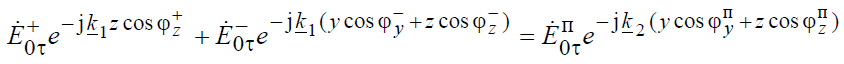.(8.5)
Для простоты положим, что обе среды являются идеальными диэлектриками (σ1 = σ2 = 0 ). В этом случае волновые коэффициенты будут чисто вещественными, а направляющие косинусы иметь очевидный геометрический смысл (рис.8.1). Чтобы равенство (8.5) соблюдалось при всех y, необходимо положить
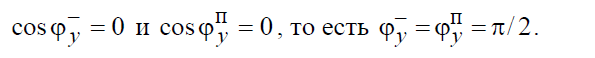
Отсюда следует, что падающий, отраженный и переломленный лучи лежат в одной плоскости (y = const). Чтобы равенство (8.5) соблюдалось при всех z, необходимо, чтобы выполнялись соотношения:
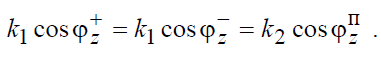
Из рис.8.1 следует, что ϕ 
. Подставляя значения ϕz в последнее равенство, можно придти к следующим соотношениям:
Выражение (8.6) устанавливает соотношение между углом падения плоской волны и углом ее отражения и является математической формулировкой известного из оптики первого закона Снеллиуса: угол отражения равен углу падения.
Формула (8.7), которую можно привести к виду:
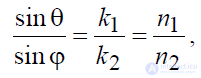, (8.8)
устанавливает соотношение между углом падения и углом преломления плоской волны и носит название закона синусов или второго закона Снеллиуса.
В (8.8) использованы обозначения
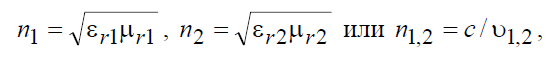, (8.9)
где n1 и n2 – коэффициенты, которые носят название показателей преломления 1-й и 2-й сред.
Если n1 > n2 то говорят, что, первая среда оптически более плотная, чем вторая. В этом случае угол преломления θ всегда будет меньше угла падения ϕ. Если же имеет место обратное соотношение n2 > n1, то вторая среда считается оптически более плотной, чем первая, и угол преломления θ в этом случае будет больше угла падения ϕ. Ход лучей для обеих ситуаций показан на рис.8.2,а,б.
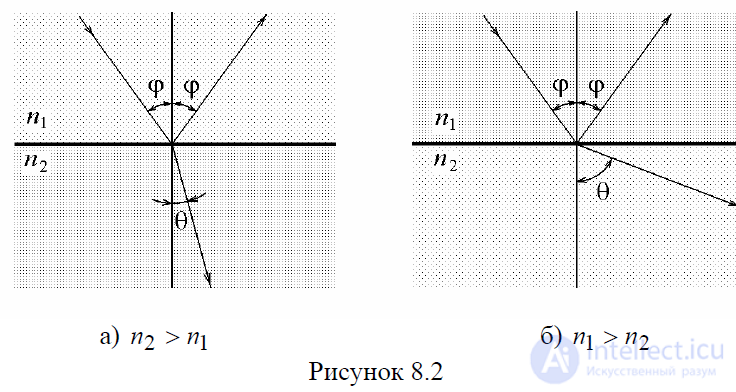
Рисунок 8.2
Резюмируя изложенное, можно сделать следующие выводы:
1) лучи падающей, отраженной и преломленной волн расположены в одной плоскости – плоскости падения;
2) угол отражения плоской волны от поверхности раздела двух сред равен углу падения;
3) углы падения и преломления плоской волны на границе раздела двух сред связаны между собой законом синусов.
Следует заметить, что соотношения (8.6) и (8.7) справедливы также и для случая проводящих сред, однако входящие сюда углы оказываются комплексными не имеют простого геометрического толкованя.
Для полноты описания явлений, сопутствующих падению плоской волны на плоскую поверхность раздела двух сред, необходимо дополнить полученные выше угловые характеристики волн, выражениями, устанавливающими соотношения между комплексными амплитудами падающей, отраженной и преломленной волн. Иногда в литературе последние соотношения называют динамическими характеристиками волн. Для удобства описания динамических характеристик вводят, так называемые, комплексные коэффициенты отражения R и прохождения T , определяемые как отношения комплексных амплитуд соответствующих волн на границе раздела двух сред:
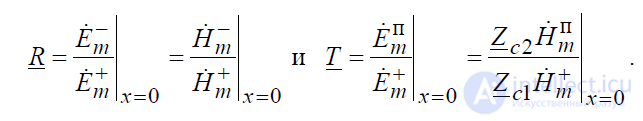. (8.10)
Коэффициенты отражения и преломления являются комплексными величинами, модули которых
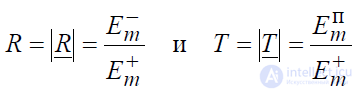
устанавливают соотношения между амплитудами падающей, отраженной и преломленной волн на границе раздела двух сред, а их аргументы
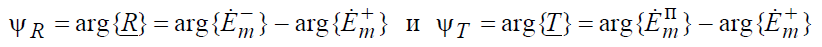– разность фаз этих волн.
Установлено, что значения коэффициентов отражения и преломления зависят от ориентации вектора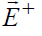 
плоской волны по отношению к ее плоскости падения, другими словами, от поляризации падающей волны. Известно, что волну любой поляризации можно представить в виде суммы двух ортогональных волн с линейной поляризацией. Поэтому для полного описания явления имеет смысл определить коэффициенты 
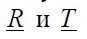для обеих этих волн, падающих на поверхность раздела. В качестве таковых выберем две волны, у одной и которых вектор 
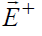лежит в плоскости падения, а у второй – перпендикулярен этой плоскости. Первой из них принято называть волной с параллельной (плоскости падения) поляризацией, а вторую – волной с нормальной (т.е. перпендикулярной к плоскости падения) поляризацией. Рассмотрим динамические характеристики для каждой из этих волн отдельно.
Пусть на плоскую границу раздела двух сред падает волна с нормальной поляризацией (рис.8.3). В этом случае в плоскости падения будут расположены векторы напряженности магнитного поля Hr падающей, отраженной и преломленной волн, а векторы Er всех волн будут ориентированы параллельно поверхности раздела. Поэтому здесь граничные условия для тангенциальных компонент напряженности электрического и магнитного полей на плоскости x = 0 можно сформулировать в виде следующих равенств:
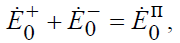
(8.11)
(8.12)
Последнее равенство можно переписать, как:
. (8.13)
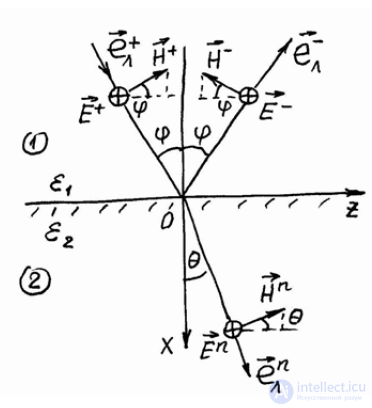
Рисунок 8.3
Разделим левые и правые части выражений (8.11) и (8.13) на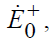 
, в результате чего получим:
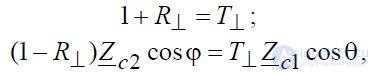
где R⊥ и T⊥ – коэффициенты отражения и преломления волны с нормальной поляризацией. Решая полученную систему уравнений относительно неизвестных R⊥ и T⊥, находим:
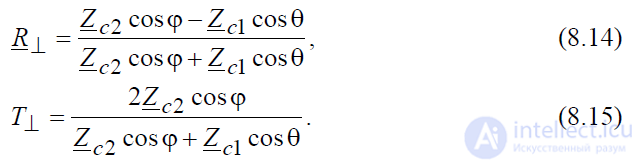
Для немагнитных диэлектриков (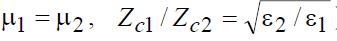 
) эти формулы с учетом 2-го закона Снеллиуса заметно упрощаются и приобретают следующий вид:
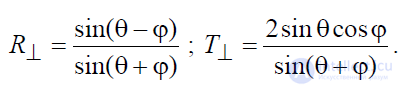(8.16)
Выражения (8.14)-(8.16) называются формулами Френеля.
Исследование, описанное в статье про отражение, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое отражение, преломление и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория электромагнитного поля
Комментарии
Оставить комментарий
Теория электромагнитного поля
Термины: Теория электромагнитного поля