Лекция
Привет, Вы узнаете о том , что такое энергия электромагнитного поля, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое энергия электромагнитного поля, теорема поинтинга, вектор поинтинга, вектор умова , настоятельно рекомендую прочитать все из категории Теория электромагнитного поля.
вектор умова — Пойнтинга (также вектор Пойнтинга ) — вектор плотности потока энергии электромагнитного поля, компоненты которого входят в состав тензора энергии-импульса электромагнитного поля . Модуль вектора Умова — Пойнтинга равен количеству энергии, переносимой через единичную площадь, нормальную к S, в единицу времени. Своим направлением вектор определяет направление переноса энергии.
В электродинамике теорема Пойнтинга — это утверждение о сохранении энергии для электромагнитных полей, разработанное британским физиком Джоном Генри Пойнтингом .Она гласит, что в заданном объеме запасенная энергия изменяется со скоростью, определяемой работой , выполненной над зарядами внутри объема, за вычетом скорости, с которой энергия покидает объем. Она строго верна только в средах, которые не являются дисперсионными , но может быть расширена для дисперсионного случая.Теорема аналогична теореме о работе-энергии в классической механике и математически подобна уравнению непрерывности .
Говоря о физической реальности ЭМП, подразумевают, что с полем связана энергия.
Изменяясь, поле может отдавать свою энергию какому-либо неэлектромагнитному процессу. Поэтому важно понять, каким законам подчиняется энергия ЭМП.
Энергия — греческое слово — означает деятельность.
Философское определение понятия энергии: энергия — это общая мера различных форм движения материи.
Физическое понимание: энергия это есть величина, которая количественно не меняется ни при каких превращениях, происходящих в природе.
Хорошо нам знакомы превращения энергии:
— механическая ^ т е п л о в а я ;
— механическая электрическая;
— электрическая ^ т е п л о в а я .
В данной лекции нас будет интересовать превращение электрической энергии в тепловую. Это превращение происходит в соответствии с законом Джоуля—Ленца.
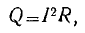
где Q — количество теплоты, выделяющейся в единицу времени в проводнике с сопротивлением Rf, при прохождении через него тока /.
Существует' однако еще один закон сохранения энергии, установленный профессором физики Новороссийского (Одесского)
университета Умовым в 1874 г.: если энергия исчезает в какой-то области пространства, то это происходит в результате того, что она вытекает через границы этой области.
Как ..сформулировать этот закон математически?
Пусть в объеме V имеется энергия W. Тогда по аналогии с законом сохранения зарядов
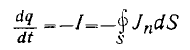(1),
можем записать (рис. 1)
( 2)
Рис. 1
Здесь Y — вектор, аналогичный .вектору плотности токов J. Как известно, вектор J равен J=pv, где р •— плотность v —скорость зарядов.
Соответственно Y определяется формулой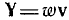 
, где w — плотность и ѵ — скорость движения энергии.
Вектор Y имеет смысл плотности потока энергии.
Его размерность
Интегральный закон сохранение (2) можно преобразовать в дифференциальный закон, аналогично тому, как (1) преобразуется
в уравнение непрерывности-
и получить
Y — вектор Умова.
Ниже, руководствуясь законом сохранения энергии (2), найдем формулировку закона сохранения энергии в электромагнитном поле. Однако предварительно мы обобщим соотношение (2)., учитывая, что энергия данного вида внутри объема может уменьшаться также за счет ее превращения в тепловую энергию.
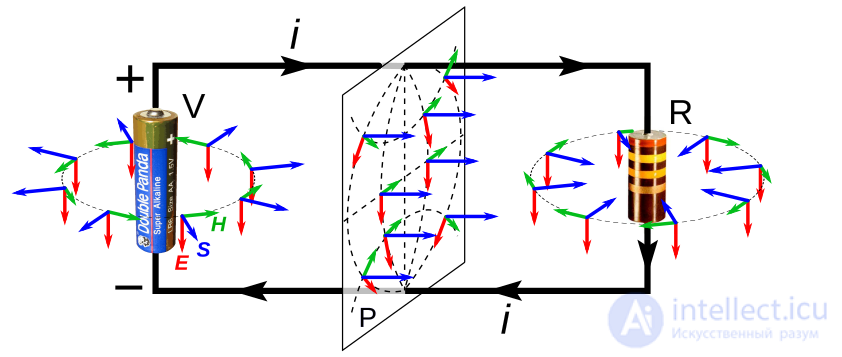
цепь постоянного тока i, соединяющая батарею V с резистором R
вектор Пойнтинга S в пространстве, окружающем цепь
напряженность электрического поля Е
напряженность магнитного поля H
Вокруг батареи вектор Умова — Пойнтинга направлен от батареи, что свидетельствует о переносе энергии из батареи; вокруг резистора вектор Умова — Пойнтинга направлен к резистору, что говорит о переносе энергии в резистор; поток вектора Умова — Пойнтинга через любую плоскость Р между батареей и резистором — направлен от батареи к резистору
Таким образом, мы будем пользоваться законом сохранения энергии в более общей формулировке, а именно:
.(3)
Итак, будем считать, что в некотором объеме V существует электромагнитное поле (рис. 2), і. е. внутри этого объема 
Сначала выразим Q через величины, характеризующие электромагнитное поле.
С учетом того (рис. 3), что
т.е.
Следовательно,
Подставив под интегралом выражение для J из второго уравнения Максвелла, получим
Далее, воспользовавшись соотношением
находим
Здесь подставляем вместо 
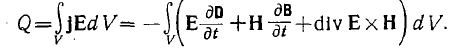. (4)
Учитывая, что согласно, теореме Остроградского—Гаусса
имеем
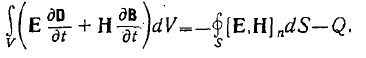(5)
Полученное соотношение (5) называется теоремой Пойнтинга.
Выясним физический смысл этой теоремы.
Для этого положим
и учтем, что
Тогда вместо (5) будем иметь
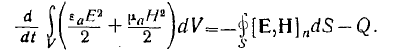(6)
Сравнивая это равенство с соотношением (3), заключаем, что
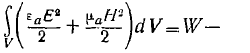
энергия электромагнитного поля в объеме V,
плотность энергии электромагнитного поля, причем:
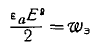— плотность электрической энергии;
—плотность магнитной энергии;
—поток-электромагнитной энергии через поверхность S;
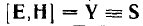— плотность потока энергии.
Вектор S называется вектором Пойнтинга.
Он был введен Пойнтингом в 1884 г.
Таким образом, теорема Пойнтинга представляет собой формулировку закона сохранения энергии в электромагнитном поле.
Теорема Пойнтинга в дифференциальной форме согласно (4) и (5) имеет вид
Рассмотрим электромагнитное поле в замкнутом объеме V, где имеются сторонние источники, заданные плотностью тока ст jr
(рис.4.1). Об этом говорит сайт https://intellect.icu . Для описания этого поля воспользуемся уравнениями Максвелла в дифференциальной форме.
Рисунок 4.1
Запишем первые два из них и умножим первое уравнение скалярно на
E r
, а второе – на H
после чего из 1-го уравнения вычтем 2-е:
Заменим левую часть полученного равенства с помощью тождества
(П2.20) и перенесем сюда первые три члена правой части, что в результате
дает:
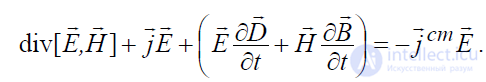. (4.1)
Теперь проинтегрируем обе части равенства (4.1) по исследуемому объему V (рис.4.1):
и, применив к первому слагаемому теорему Гаусса-Остроградского (П2.24),
приходим к следующему соотношению:
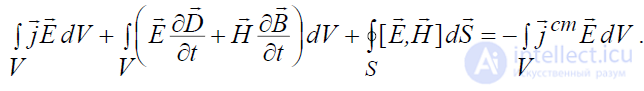. (4.2)
Полученное равенство представляет собой математическую формулировку теоремы Умова-Пойнтинга в интегральной форме, которая устанавливает
баланс электромагнитной энергии в замкнутом объеме в любой момент времени. Рассмотрим, какой физический смысл имеет здесь каждое из слагаемых.
1. Первое слагаемое.
Преобразуем его, воспользовавшись законом Ома в дифференциальной
форме, и обозначим символом Pd :
. (4.3)
Покажем, что данное выражение является математическим выражением
закона Джоуля-Ленца, а Pd – это мощность тепловых (или джоулевых) потерь, которую электромагнитное поле затрачивает на нагревание объема V.
Для этого рассмотрим простой пример. Пусть исследуемая область пространства V занята проводящей средой, а ее форма представляет собой цилиндр, ось которого направлена вдоль силовых линий напряженности электрического поля (рис.4.2).
Рисунок 4.2
Будем полагать, что размеры цилиндра настолько
малы, что векторы E
r
и j
r
во всех точках внутри
его объема одинаковы. В таком случае они не зависят от переменных интегрирования и их можно вынести из интеграла, который преобразуется к следующему виду
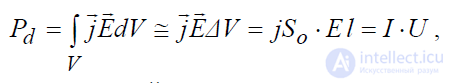
где I = jSо – ток, протекающий через основание цилиндра Sо , U = E ⋅ l –
разность потенциалов (напряжение) между основаниями цилиндра. В таком
виде данное выражение описывает известный из теории цепей закон Джоуля-Ленца о мощности Pd , выделяемой током на участки цепи длиной l.
Следует отметить, что мощность потерь Pd может принимать только положительные значения или нуль, поскольку подынтегральная функция в (4.3)
по определению не отрицательная. Равенство Pd = 0 справедливо только в случае отсутствия в среде токов, либо когда σ→∞ (идеальный проводник).
2. Второе слагаемое в (4.2) преобразуем следующим образом. Воспользовавшись материальными уравнениями 
, заменим в нем
векторы 
соответственно. Учитывая, что операции интегрирования по координатам и дифференцирования по времени взаимно не зависимы, второе слагаемое можно преобразовать к следующему виду:
.
Принимая во внимание, что э 2
w = εE2 – объемная плотность электриче-
ской энергии, а 2 2
wм = μH – объемная плотность магнитной энергии внут-
ри объема V, перепишем последнее выражение в виде:
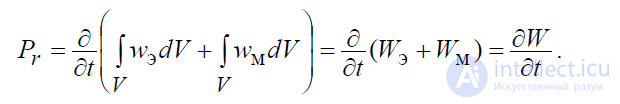. (4.4)
Здесь = ∫
V
Wэ wэdV – полная энергия электрического поля, а = ∫
V
Wм wмdV
– полная энергия электрического поля, запасенные в объеме V.
Таким образом, второе слагаемое Pr в (4.2) – это скорость изменения
суммарной энергии W =Wэ +Wм , электрической и магнитной, запасенной в
объеме V. Если Pr > 0 , то запас энергии в V растет, а если Pr < 0 , то запасенная энергия убывает.
3. Третье слагаемое перепишем так:
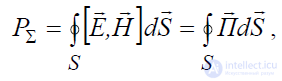(4.5)
где введено обозначение П [E,H]
r r r
= . Вектор П
r
имеет размерность [Вт/м2],
который носит название вектора Пойнтинга, определяет величину и направление движения плотности потока мощности электромагнитного поля в каждой точке рассматриваемого пространства. Следовательно, PΣ – это поток
мощности, проходящий через поверхность S, ограничивающую рассматриваемый объем V (рис.4.1). Если направление вектора П
r
совпадает направлением внешней нормали к поверхности S, то энергия ЭМП выходит из объема V наружу и 0 > Σ P . Если наоборот, направление вектора П
r
противоположно направленю внешней нормали к поверхности S , то энергия ЭМП входит в объем V извне, в этом случае PΣ < 0 .
4. Слагаемое в правой части равенства (4.2) определяет мощность сторонних источников, действующих в объеме V:
. (4.6)
Таким образом, уравнение (4.2), описывающее баланс мощности элек-
тромагнитного поля в замкнутом, может быть записано в следующем виде:
Pст = Pd + PΣ + Pr , (4.7)
откуда следует, что мощность сторонних источников в замкнутом объеме V
может расходоваться на нагревание материала, накопление энергии в объеме
и излучение энергии из данного объема.
Если сторонние источники ЭМП в рассматриваемом объеме отсутствуют
0 = ст j
r
, то и Pст = 0; в этом случае равенство (4.7) принимает вид:
Pd + PΣ + Pr = 0. (4.8)
Поскольку всегда Pd ≥ 0 , равенство (4.8) может быть справедливо в сле-
дующих случаях:
а) Pd = PΣ = Pr = 0 – замкнутый объем, заполненный непроводящей сре-
дой без потерь, запасенная энергия внутри которого остается неизменной;
б) PΣ < 0 , Pr ≥ 0, Pd ≥ 0 – энергия в рассматриваемый объем поступает
извне через окружающую его поверхность S; эта энергия здесь тратится на
нагревание и (или) на накопление энергии среды внутри объема V;
в) Pr < 0, PΣ ≥ 0 , Pd ≥ 0 – запасенная ранее в объеме V энергия уменьша-
ется (например, разряжается конденсатор) и тратится на нагревание среды
внутри V и (или) излучение за пределы объема V через окружающую его по-
верхность S.
Предположим, что в рассматриваемой области пространства существует электромагнитное поле, плотность потока мощности которого в каждой
точке характеризуется вектором Пойнтинга П
r
.
Мысленно выделим в данной области небольшой объем V в виде цилиндра (рис.4.3).
Рисунок 4.3
Сечение цилиндра S0 и его длину Δl выберем настолько малыми, чтобы вектор Пойнтинга во всех точках внутри его можно было считать одинаковым. Энергия
ЭМП, двигаясь вдоль оси z со скоростью vэ r и проходя через основание цилиндра, заполнит его за время Δt , при этом величина энергии внутри цилиндра составит:
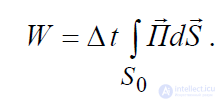. (4.9)
С другой стороны, полную энергию ЭМП в объеме цилиндра можно определить через ее плотность w во всех точках рассматриваемой области, полагая, что она известна:
. (4.10)
Приравнивая выражения (4.9) и (4.10), приходим к равенству:
,откуда найдем скорость движения энергии, как предел отношения:
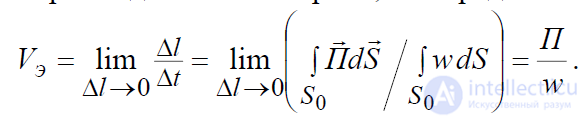. (4.11)
Поскольку направление движения энергии совпадает с направлением век-
тора Пойнтинга, то это равенство можно переписать в векторной форме:
Найдем выражение, определяющее баланс энергии для монохроматического ЭМП. Для этого запишем два первых уравнения Максвелла в комплексной форме, из них первое для комплексно-сопряженных полей:
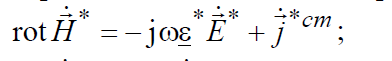(4.13)
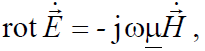, (4.14)
где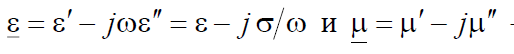 
– комплексные диэлектрическая и магнитная проницаемости среды.
Умножим уравнение (4.13) скалярно на ( E& r
− ), а уравнение (4.14) – на
( * H& r
), после чего сложим их:
Проинтегрировав полученное выражение по рассматриваемому объему
использовав тождества (П2.20) и (П2.24), приходим к равенству:
, (4.15)
которое есть математическое выражение теоремы Умова-Пойнтинга в ком-
плексной форме, описывающее баланс электромагнитной энергии монохро-
матического ЭМП в выделенном объеме V.
Рассмотрим физический смысл всех слагаемых, входящих в равенство
(4.15):
а)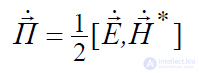 
= – комплексный вектор Пойнтинга, вещественная часть которого представляет собой плотность потока мощности, усредненый за период колебаний;
б)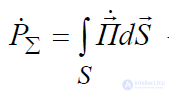 
– комплексная мощность, излучаемая из объема V, а ее вещественная часть Re{P&Σ} – это излучаемая из объема V , усредненная за период колебаний;
в)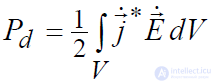 
– средняя за период мощность потерь (активная);
г) 
j – мнимая мощность в объеме V, которую можно преобразовать к следующему виду:
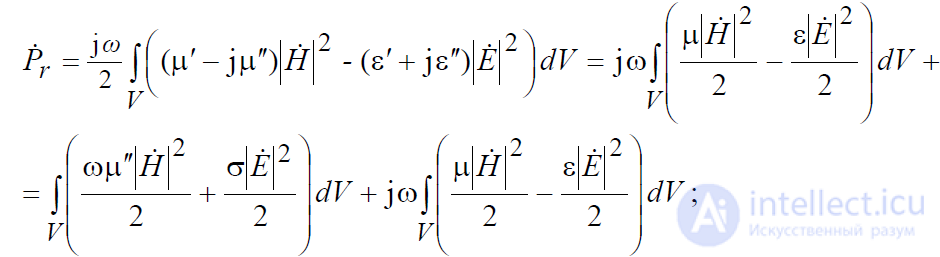
1 – комплексная мощность сторонних источников.
Выделим из уравнения (4.15) равенства для действительной и мнимой
частей:
(4.16)
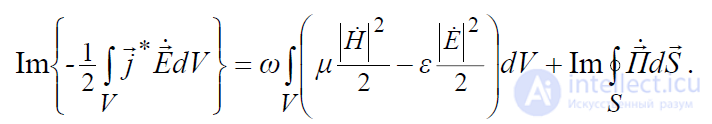(4.17)
Первое из этих равенств (4.16) характеризует баланс активных мощностей, которые представляют собой реальные мощности, усредненные за период колебаний. Левая часть этого равенства описывает усредненную за период колебаний мощность, поступающую в объем V от стороннего источника. Эта мощность расходуется здесь на нагревание среды и излучение из данного объема через ограничивающую его поверхность. Второе уравнение
(4.17) описывает баланс реактивных (колебательных) мощностей, которые одну половину периода переходят от источника поля в рассматриваемый объем, а во вторую половину – поступают назад в источник.
Пусть векторы электромагнитного поля во времени меняются
пи гармоническому-закону, т. е.
Тогда среднее значение вектора S за период Т равно
т. е.
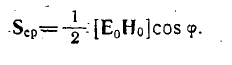. (9)
С другой- стороны, записывая (8) в комплексной форме
видим, что
Сравнивая последние равенства с (9), находим, что
Наиболее просто ввести в теорему Пойнтинга источники электромагнитного
поля, представляя их сторонними э.д.с. В теории электрических цепей сторонняя э.д.с. сосредоточена в одном месте. Но для того, чтобы ввести стороннюю э.д.с. в уравнения электромагнитного
поля, мы должны считать, что она может быть распределона в пространстве и вместо еСтор оперировать напряженностью
поля сторонней э.д.с. Е с т о р .
Закон Ома в дифференциальной форме с учетом сторонней э.д.с.
будет представляться в виде-
от сюда
Подставляя это выражение для Е в уравнение (4) слева, после
некоторых преобразований получим
(7)
поскольку
Соотношение (7) является формулировкой закона сохранения энергии электромагнитного поля при наличии источников. Видно, что энергия источника расходуется на увеличение электромагнитной энергии -в объеме V, на поток энергии из объема и на джоулево тепло.
В дифференциальной форме (7) записывается так:
Энергия электромагнитного поля, теорема и вектор Поинтинга имеют важные приложения в физике и инженерии. Вот основные примеры их применения:
теорема поинтинга и связанный с ней вектор описывают поток энергии электромагнитного поля. Это применяется при анализе:
Энергетических потерь в линиях передачи.
Эффективности передачи энергии в волноводах и антеннах.
Распределения энергии в электрических машинах (например, генераторах).
Вектор Поинтинга помогает моделировать и понимать процессы излучения и распространения радиоволн, которые используются:
В радиосвязи и телевещании.
В современных технологиях связи (Wi-Fi, 5G).
Энергетические характеристики излучающих элементов антенн, такие как излучаемая мощность и диаграмма направленности, определяются с помощью вектора Поинтинга.
Энергия электромагнитного поля играет ключевую роль в исследовании и разработке:
Лазерных систем, где важен контроль плотности энергии.
Оптических систем, где передача света анализируется с помощью уравнений Максвелла.
Теорема Поинтинга используется для расчета теплового воздействия электромагнитного поля на проводники или биологические ткани, например:
В микроволновой обработке материалов.
При оценке безопасности электромагнитных излучений.
Применяется в таких устройствах, как электромагнитные двигатели, где циркуляция энергии рассчитывается для оптимизации работы системы.
Исследование, описанное в статье про энергия электромагнитного поля, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое энергия электромагнитного поля, теорема поинтинга, вектор поинтинга, вектор умова и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория электромагнитного поля
Комментарии
Оставить комментарий
Теория электромагнитного поля
Термины: Теория электромагнитного поля