Привет, мой друг, тебе интересно узнать все про построение броуновского движения, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое
построение броуновского движения , настоятельно рекомендую прочитать все из категории вероятностные процессы.
.
построение броуновского движения по функциям Шаудера и последовательности независимых гауссовских величин: а) две леммы; б) построение на [0,1]; в) построение на [0,¥].
Определение броуновского движения и его существование
Одним из важнейших случайных процессов является винеровский процесс, называемый также броуновским движением.
Определение 4.1. Случайный процесс {W(t), t > 0} называется стандартным броуновским движением, если
1) W(0) = 0 п.н.;
2) приращения процесса W(t1), W(t2) − W(t1), . . . , W(tm) − W(tm−1) при любых m ∈ N и t1, t2, . . . , tm таких, что 0 < t1 < t2 < · · · < tm, являются независимыми случайными величинами;
3) случайная величина W(t) − W(s) имеет нормальное распределение с параметрами 0 и t − s при любых t, s таких, что
0 6 s < t;
4) траектории процесса {W(t)} п.н. непрерывны.
Можно дать и другое определение броуновского движения.
Определение 4.2. Случайный процесс {W(t), t > 0} называется стандартным броуновским движением, если
1) W(0) = 0 п.н.;
2) случайный вектор {W(t1), W(t2), . . . , W(tm)} имеет многомерное нормальное распределение при любых m ∈ N и
t1, t2, . . . , tm таких, что 0 < t1 < t2 < · · · < tm;
3) EW(t) = 0 при любом t ∈ [0,∞), cov (W(t1), W(t2)) = min (t1, t2) при любых t1, t2 ∈ [0,∞);
4) траектории процесса {W(t)} п.н. непрерывны.
Прежде, чем доказывать эквивалентность этих определений,
напомним некоторые сведения о нормальных распределениях. Говорят, что случайная величина ξ имеет нормальное распределение
с параметрами a ∈ R и σ
2 ∈ (0,∞) (обозначение: ξ ∼ Na, σ2�),
если ξ является непрерывной случайной величиной с плотностью
вероятностей
Нормальное распределение называется стандартным, если a = 0,σ2 = 1. Функция распределения в этом случае обозначается Φ(x)
и называется функцией Лапласа
Пусть ξ1, ξ2, . . . , ξn – независимые случайные величины и ξi ∼
N(0, 1) при i = 1, 2, . . . , n. Рассмотрим случайный вектор ξ =
{ξ1, ξ2, . . . , ξn}. Пусть A и b – произвольные числовые матрицы
размеров n×n и n×1. Распределения случайных векторов Aξ +b
(здесь случайные векторы представлены в виде столбцов) и только они называются n-мерными нормальными распределениями.
Случайные векторы с такими распределениями называются нормальными.
Если {η1, η2, . . . , ηn} – нормальный вектор и cov (ηi
, ηj ) = 0 при
всех i, j таких, что i 6= j, то случайные величины η1, η2, . . . , ηn являются независимыми. Если же cov (ηi
, ηj ) = 0 при всех i, j таких,
что i 6 k, j > k для некоторого k ∈ {1, 2, . . . , n − 1}, то случайные
векторы {η1, η2, . . . , ηk} и {ηk+1, ηk+2, . . . , ηn} являются независимыми.
Доказательство эквивалентности. Очевидно,

, (4.2)
где A – матрица, обратная к первой матрице в правой части (4.1).
Если W удовлетворяет условиям определения 1, то случайный вектор {W(t1), W(t2) − W(t1), . . . , W(tm) − W(tm−1)} является нормальным, откуда, ввиду (4.2), случайный вектор
{W(t1), W(t2), . . . , W(tm)} также является нормальным. Далее, при t2 > t1
(здесь учтено, что W(t1) и (W(t2) − W(t1)) – независимые случайные величины и поэтому EW(t1) (W(t2) − W(t1)) = 0).
Если же W удовлетворяет условиям определения 4.2, то ввиду (4.1) из того, что вектор {W(t1), W(t2), . . . , W(tm)} является нормальным, следует, что и вектор {W(t1), W(t2) − W(t1), . Об этом говорит сайт https://intellect.icu . . . ,
W(tm)−W(tm−1)} нормальный. Его компоненты некоррелированы, т.к. при j > i
поэтому случайные величины W(t1), W(t2) − W(t1), . . . , W(tm) − W(tm−1) являются независимыми. Наконец,
Эквивалентность доказана.
Докажем существование броуновского движения. Зададим его явную конструкцию, исходя из последовательности независимых случайных величин с одинаковым распределением N(0, 1) и функций Шаудера.
Дадим их определение, но сначала напомним определение
функций Хаара. Эти функции обозначаются Hi(t), i ∈ N, и задаются на отрезке [0, 1]. Функция H1 тождественно равна 1. Для
каждого n ∈ N0 (N0 = {0, 1, 2, . . . }) введем 2
n функций Хаара
H2n+k, где k = 1, 2, . . . , 2
n. Для этой цели разобьем отрезок [0, 1] на 2 n равных отрезков и пронумеруем их слева направо. Возьмем k-й такой отрезок. Вне его положим H2n+k(t) = 0. Разделим указанный отрезок пополам. На левой его половине положим H2n+k(t) = 2−n/2
, а на правой – положим H2n+k(t) = −2−n/2 (см. рис. 2).
Рассмотрим пространство L2[0, 1] измеримых числовых функций x, заданных на отрезке [0, 1] и интегрируемых в квадрате:
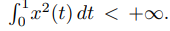
Известно, что функции Хаара образуют полную ортонормированную систему в пространстве L
2[0, 1] со скалярным произведением
Рис. 2.
Поэтому любую функцию x ∈ L2[0, 1] можно разложить в ряд по
этой системе функций:
и выполнено равенство Парсеваля:
Построим непрерывные неотрицательные функции Si(t), называемые функциями Шаудера, на основе Hi(t):
Si(t) = Z t0Hi(s) ds, i ∈ N.
Очевидно, что при i ∈
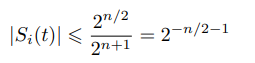
(4.3)
и при разных
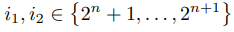
функции Si1 (t), Si2
(t) имеют непересекающиеся носители.
Установим два вспомогательных утверждения.
Лемма 4.1. Пусть числовая последовательность {ai, i ∈ N} такова, что ai = O (iε) при i → ∞ для некоторого ε ∈ (0, 1/2).
Тогда ряд
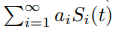
сходится равномерно по t на отрезке [0, 1].
Доказательство. Существует такая положительная постоянная K, что при всех i ∈ N выполняется неравенство

,
поэтому при всех
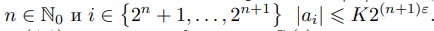
.
Откуда, учитывая (4.3) и то, что функции Si(t) при разных
имеют попарно непересекающиеся носители, получаем, что при всех t ∈ [0, 1]
.
Следовательно, при m ∈ N0, t ∈ [0, 1]
,
но правая часть стремится к нулю при m → ∞. Лемма доказана.
Лемма 4.2. Пусть ξ1, ξ2, . . . – случайные величины, заданные на одном вероятностном пространстве (Ω, F, P), причем
ξi ∼ N(0, 1), i ∈ N. Тогда для произвольной постоянной c ∈
√
2,∞
�
и почти всех (п.в.) ω ∈ Ω существует такое натуральное число N0 (c, ω), что при всех i > N0 (c, ω) будет |ξi
| < c√
ln i.
Доказательство. Нам потребуется лемма Бореля–Кантелли, утверждающая, что если случайные события A1, A2, . . . таковы, что P∞
i=1 P (Ai) < +∞, то для п.в. ω произойдет лишь конечное число событий из A1, A2, . . . . Заметим, что если ξ ∼ N(0, 1),
то при x > 0
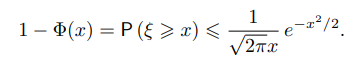
. (4.4)
Действительно,
.
Поэтому при i > 2
При c > √2 ряд
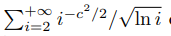
сходится. Следовательно, для
п.в. ω лишь для i из конечного множества выполняется неравенство |ξi(ω)| > c
√
ln i. Лемма доказана.
Теорема 4.1. Пусть ξ1, ξ2, . . . – независимые случайные величины, причем ξi ∼ N(0, 1), i ∈ N; S1,S2, . . . – функции Шаудера,
тогда
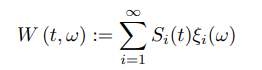
(4.5)
является броуновским движением при t ∈ [0, 1].
Доказательство. В силу лемм 4.1 и 4.2 для п.в. ω ряд в правой части (4.5) сходится равномерно по t на отрезке [0, 1]. Функции Si(t) непрерывны по t при любом i ∈ N. Следовательно, для
п.в. ω правая часть (4.5) является непрерывной по t функцией.
Покажем, что ряд в правой части (4.5) сходится в среднем
квадратическом. Напомним, что если η, η1, η2, . . . – случайные величины, заданные на одном вероятностном пространстве, то сходимость в среднем квадратическом случайной последовательности {ηn} к η при n → ∞ (обозначение: ηn
ср. кв. → η) означает, что
limn→∞ E (ηn − η)
2 = 0; случайная последовательность {ηn} сходится в среднем квадратическом при n → ∞ тогда и только тогда,
когда E (ηm − ηl)
2 → 0 при m, l → ∞. Аналогично вводится понятие сходимости в среднем квадратическом для последовательности случайных векторов. Имеем при m > l, что
Вспоминая свойства функций Шаудера, видим, что
Следовательно,
что означает требуюмую сходимость в среднем квадратическом.
Поскольку и сходимость п.н., и сходимость в среднем квадратическом влекут сходимость по вероятности, то пределы правой части (4.5) в обоих случаях будут равны п.н.
Покажем справедливость свойств 1), 2), 3) определения 4.2
броуновского движения.
1) Поскольку Si(0) = 0 для всех i ∈ N, то W(0) = 0 п.н.
2) Предел в среднем квадратическом последовательности нормальных случайных векторов является нормальным случайным
вектором. Поскольку для m ∈ N и t1, . . . , tm ∈ (0, 1] при n → ∞
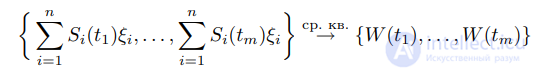
(4.6)
и вектор слева является нормальным, то и вектор справа является
нормальным.
3) Из соотношения (4.6) следует сходимость математических
ожиданий и ковариаций компонент случайного вектора в левой
части, поэтому при n → ∞
а)
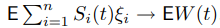
, но левая часть равна нулю, следовательно, EW(t) = 0 при любом t ∈ [0, 1];
б)
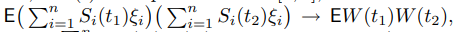
но левая часть равна Pn
i=1 Si(t1)Si(t2) и ее предел равен (вспомним равенство Парсеваля)
следовательно, EW(t1)W(t2) = min (t1, t2) при t1, t2 ∈ [0, 1] (здесь
I[a,b] (·) – индикатор отрезка [a, b]).
Теорема доказана.
Замечание 4.1. Используя процедуру пополнения вероятностного пространства, на котором заданы случайные величины ξ1, ξ2, . . . , и полагая W (t, ω) = 0 при t ∈ [0, 1] и тех ω, для которых ряд в правой части (4.5) не сходится равномерно по t на отрезке [0, 1], получаем броуновское движение, все траектории которого
непрерывны. В дальнейшем будем рассматривать именно такое броуновское движ
В заключение обсудим вопрос о построении броуновского движения при всех t ∈ [0,∞). Для этой цели рассмотрим последовательность независимых броуновских движений W1, W2, . . . , заданных при t ∈ [0, 1], и положим W(t) = W1(t) при t ∈ [0, 1],
W(t) = W1(1) + W2 (t − 1) при t ∈ [1, 2], W(t) = W1(1) + W2(1) + W3 (t − 2) при t ∈ [2, 3] и т.д. Полученный процесс W и является броуновским движением на полуоси [0,∞) (доказательство предоставляется читателю). В связи с указанным построением уместно упомянуть так называемое марковское свойство
броуновского движения W: для каждого t0 ∈ (0, +∞) случайный процесс {W (t0 + t) − W(t0), t ∈ [0, +∞)} является броуновским движением, причем не зависящим от прошлого, т.е. процесса {W(t), t ∈ [0, t0]}.
Построение броуновского движения, индексированного множествами, с помощью функций Хаара проводится в работе
Руке R. The Haar-function constraction of Brownian motion indexed by sets // Z. Wahr. verw. Geb. - 1983. - Bd. 64, H. 4. - S. 523-539.
Напиши свое отношение про построение броуновского движения. Это меня вдохновит писать для тебя всё больше и больше интересного. Спасибо Надеюсь, что теперь ты понял что такое построение броуновского движения
и для чего все это нужно, а если не понял, или есть замечания,
то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
вероятностные процессы
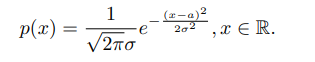
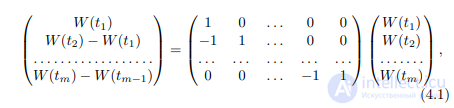
 , (4.2)
, (4.2)
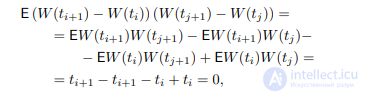

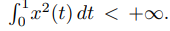 Известно, что функции Хаара образуют полную ортонормированную систему в пространстве L2[0, 1] со скалярным произведением
Известно, что функции Хаара образуют полную ортонормированную систему в пространстве L2[0, 1] со скалярным произведением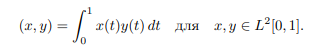

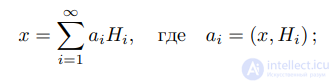
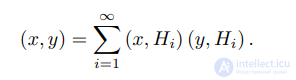
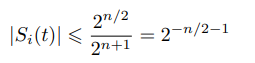 (4.3)
(4.3)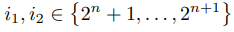 функции Si1 (t), Si2
функции Si1 (t), Si2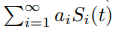 сходится равномерно по t на отрезке [0, 1].
сходится равномерно по t на отрезке [0, 1].
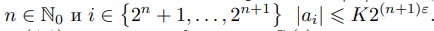
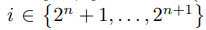
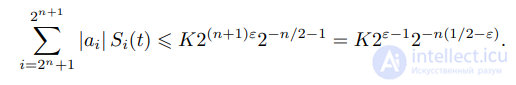
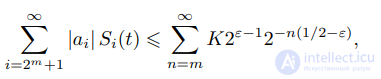
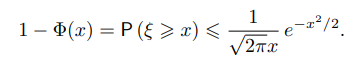 . (4.4)
. (4.4)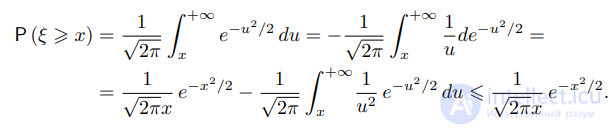
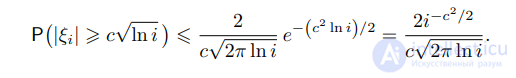
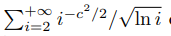 сходится. Следовательно, для
сходится. Следовательно, для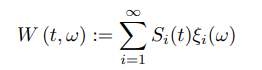 (4.5)
(4.5)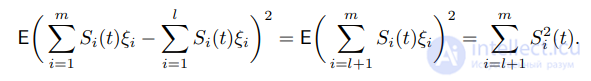
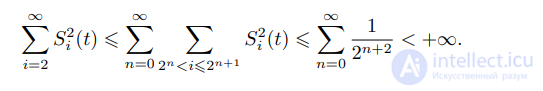
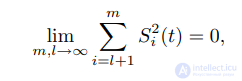
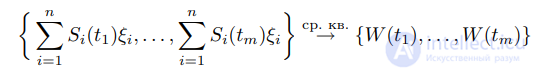 (4.6)
(4.6)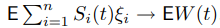 , но левая часть равна нулю, следовательно, EW(t) = 0 при любом t ∈ [0, 1];
, но левая часть равна нулю, следовательно, EW(t) = 0 при любом t ∈ [0, 1];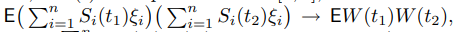 но левая часть равна Pn
но левая часть равна Pn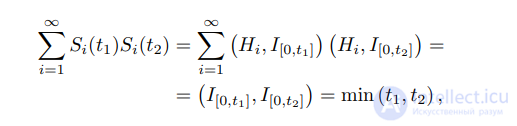
Комментарии
Оставить комментарий
вероятностные процессы
Термины: вероятностные процессы