Лекция
Привет, Вы узнаете о том , что такое теория типов, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое теория типов, базовые вычислительные формализмы, семантические стили, вычислительные формализмы , настоятельно рекомендую прочитать все из категории Структуры данных.
В математике, логике и информатике теорией типов считается какая-либо формальная система, являющаяся альтернативой наивной теории множеств, сопровождаемая классификацией элементов такой системы с помощью типов, образующих некоторую иерархию. Также под теорией типов понимают изучение подобных формализмов.
теория типов — математически формализованная база для проектирования, анализа и изучения систем типов данных в теории языков программирования (раздел информатики). Многие программисты используют это понятие для обозначения любого аналитического труда, изучающего системы типов в языках программирования. В научных кругах под теорией типов чаще всего понимают более узкий раздел дискретной математики, в частности λ-исчисление с типами.
Современная теория типов была частично разработана в процессе разрешения парадокса Рассела и во многом базируется на работе Бертрана Рассела и Альфреда Уайтхеда «Principia mathematica» .
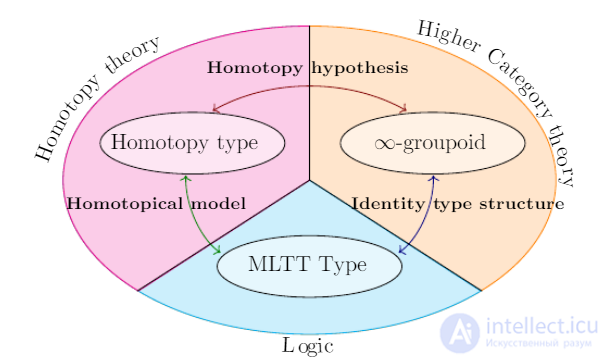
Рисунок 1 Гомотопический тринитаризм как связь логических понятий, гомотопические понятия и алгебраические структуры
1901 — парадокс Рассела
1908 — первая теория типов (Рассел, Уайтхед)
1900-1930 Теория множеств и порочные круги (vicious circles). Проблема импредекативности.
1925 — простая теория типов Рамсея Системы “простых типов” (simply typed lambda calculus)
1930-1950 Соответствие Карри-Ховарда
1940 — простое типизированное λ-исчисление
1950-1970 Зависимые типы. Authomath де-Брюина.
1973 — конструктивная теория типов (Мартин-Леф)

Доктрина типов восходит к Б. Расселу, согласно которому всякий тип рассматривается как диапазон значимости пропозициональной (высказывательной) функции. Помимо того, считается, что у всякой функции имеется тип (ее домен, область определения). В доктрине типов соблюдается выполнимость принципа замены типа (высказывания) на дефинициально эквивалентный тип (высказывание).
В основе этой теории лежит принцип иерархичности. Это означает, что логические понятия — высказывания, индивиды, пропозициональные функции — располагаются в иерархию типов. Существенно, что произвольная функция в качестве своих аргументов имеет лишь те понятия, которые предшествуют ей в иерархии.
Под некоторой теорией типов обычно понимают прикладную логику высших порядков, в которой имеется тип N натуральных чисел и в которой выполняются аксиомы арифметики Пеано
Исторически первой предложенной теорией типов (период с 1902 по 1913) является Разветвленная теория типов (Ramified Theory of Types, RTT), построенная Уайтхедом и Расселом, и окончательно сформулированная в фундаментальной работе «Principia Mathematica». В основе данной теории лежит принцип ограничения числа случаев, когда объекты принадлежат единому типу. Явным образом объявляется восемь таких случаев и различаются две иерархии типов: (просто) «типы» и «порядки». При этом сама нотация «типа» не определена, и имеется ряд других неточностей, т.к. главным намерением было объявить неравными типы функций от разного числа аргументов или от аргументов разных типов . Неотъемлемой составляющей теории является аксиома редуцируемости.
В 1920-х Чвистек и Рамси предложили неразветвленную теорию типов, ныне известную как «Теория простых типов» или Простая теория типов (Simple Type Theory), которая сворачивает иерархию типов, устраняя необходимость в аксиоме редуцируемости.
Простая теория типов разрешала теоретико-множественные парадоксы, но семантические парадоксы второй группы, парадоксы Греллинга-Нельсона
и т.д., оставались неразрешенными, для которых Расселом и Уайтхедом была разработана разветвленная теория типов в рамках системы Principia Mathematica.
Интуиционистскую теорию типов (Intuitionistic Type Theory, ITT) построил Пер Мартин-Леф.
Интуиционистская теория типов (также известная как теория конструктивных типов или теория типов Мартина-Лефа ) - это теория типов и альтернативная основа математики . Интуиционистская теория типов была создана Пером Мартином-Лефом , шведским математиком и философом , который впервые опубликовал ее в 1972 году. Существует несколько версий теории типов: Мартин-Леф предложил как интенсиональный, так и экстенсиональный варианты теории и ранние импредикативные версии, доказанная парадоксом Жирара непоследовательность , уступила место предикативномуверсии. Однако все версии сохраняют базовую конструкцию конструктивной логики с использованием зависимых типов.
Мартин-Леф разработал теорию типов на принципах математического конструктивизма . Конструктивизм требует, чтобы любое доказательство существования содержало «свидетеля». Таким образом, любое доказательство того, что «существует простое число больше 1000», должно идентифицировать конкретное число, которое одновременно является простым и больше 1000. Интуиционистская теория типов достигла этой цели дизайна, усвоив интерпретацию BHK . Интересным следствием является то, что доказательства становятся математическими объектами, которые можно исследовать, сравнивать и манипулировать.
Конструкторы типов в интуиционистской теории типов были построены так, чтобы следовать взаимно однозначному соответствию с логическими связками. Например, логическая связка под названием импликация ( ) соответствует типу функции (
). Это соответствие называется изоморфизмом Карри – Ховарда . Предыдущие теории типов также следовали этому изоморфизму, но Мартин-Леф был первым, кто расширил его до логики предикатов , введя зависимые типы .
Интуиционистская логика. Hет правила исключенного третьего. Любое док-во должно быть предъявлено в общем виде
В интуиционистской теории типов есть 3 конечных типа, которые затем составляются с использованием 5 различных конструкторов типов. В отличие от теорий множеств, теории типов не строятся на логике, подобной логике Фреге . Итак, каждая особенность теории типов выполняет двойную функцию как свойство математики и логики.
Если вы не знакомы с теорией типов и знакомы с теорией множеств, краткое изложение: Типы содержат термины так же, как множества содержат элементы. Термины относятся к одному и только одному типу. Такие термины, как а также
вычислить ("уменьшить") до канонических терминов, например 4. Подробнее см. в статье о теории типов .
Есть 3 конечных типа: Тип 0 содержит 0 терминов. Тип 1 содержит 1 канонический термин. А 2-й тип содержит 2 канонических термина.
Поскольку тип 0 содержит 0 терминов, он также называется пустым типом . Он используется для обозначения всего, чего не может быть. Также написано и представляет что-либо недоказуемое. (То есть доказательства этого не может существовать.) В результате отрицание определяется как функция по отношению к нему:
.
Аналогично, тип 1 содержит 1 канонический термин и представляет существование. Об этом говорит сайт https://intellect.icu . Его еще называют типом агрегата . Он часто представляет собой утверждения, которые можно доказать, и поэтому иногда их пишут. .
Наконец, 2-й тип содержит 2 канонических термина. Он представляет собой определенный выбор между двумя ценностями. Он используется для логических значений, но не для предложений. Предложения считаются 1-м типом, и может быть доказано, что у них никогда не будет доказательства ( тип 0 ), или они могут не быть доказаны в любом случае. ( Закон исключенного среднего не распространяется на предложения в интуиционистской теории типов.)
Теория чистых систем типов (англ. pure type systems, PTS) обобщает все исчисления лямбда-куба и формулирует правила, позволяющие вычислить их как частные случаи. Ее независимо построили Берарди (Berardi) и Терлоу (Terlouw). Чистые системы типов оперируют только понятием типа, рассматривая все понятия других исчислений только в виде типов — потому они и называются «чистыми». Не производится разделения между термами и типами, между различными слоями (т.е. рода́ типов также называются типами, только относящимися к другой вселенной), и даже сами слои называются не сортами, а типами (точнее, вселенными типов). В общем виде, чистая система типов задается понятием спецификации, пятью жесткими правилами и двумя гибкими (меняющимися от системы к системе). Спецификация чистой системы типов представляет собой тройку (S,A,R), где S — множество сортов (Sorts), A — множество аксиом (Axioms) над этими сортами и R — множество правил (Rules).
Теории типов высших размерностей (англ. higher-dimensional type theories) или просто Высшие теории типов (higher type theories, HTT) обобщают традиционные теории типов, разрешая устанавливать нетривиальные отношения равенства между типами. Например, если взять множество пар (декартовых произведений) натуральных чисел nat × nat и множество функций, возвращающих натуральное число nat -> nat, то нельзя утверждать, что элементы этих множеств попарно равны, но можно утверждать, что эти множества эквивалентны. Изоморфизмы между типами и изучаются в двухмерной, трехмерной и т.д. теориях типов. Весь необходимый базис для формулировки этих теорий был заложен еще Жираром — Рейнольдсом, но сами теории были сформулированы много позже.
Гомотопическая теория типов (англ. homotopy type theory, HoTT) обобщает многомерные теории, устанавливая равенства типов на уровне топологий. В многомерных теориях понятия «эквивалентности типов» и «равенства типов» считаются различными. Радикальным нововведением гомотопической теории является аксиома унивалентности, постулирующая, что если типы топологически эквивалентны, то они топологически равны.
Лямбда-исчисление (λ-исчисление) — формальная система, разработанная американским математиком Алонзо Черчем для формализации и анализа понятия вычислимости.
Чистое λ-исчисление, термы которого, называемые также объектами («обами»), или λ-термами, построены исключительно из переменных применением аппликации и абстракции. Изначально наличие каких-либо констант не предполагается.
Лямбда исчисление – самый простой и элегантный алгоритмически полный язык программирования.
Простое типизированное лямбда исчисление. Алгоритмически неполно. Любой терм (в том числе, со свободными переменными) имеет нормальную (каноническую, “вычисленную”) форму.
| t ::= | термы: |
| x | переменная |
| λx. t | абстракция |
| t t | применение |
Примеры
(λx.x) z
(λx.x) ((λx.x) (λz. (λx.x) z))
Вычисление (β-редукция)
(λx.x) ((λx.x) (λz. (λx.x) z))
id (id (λz. id z))
→ id (id (λz.z))
→ id (λz.z)
→ λz.z
Кодирование в терминах λ-исчисления
Основная форма эквивалентности, определяемая в лямбда-термах, это альфа-эквивалентность. Например, и
: альфа-эквивалентные лямбда-термы и оба представляют одну и ту же функцию (функцию тождества). Термы
и
не альфа-эквивалентны, так как они не находятся в лямбда-абстракции.
β-редукция
Поскольку выражение обозначает функцию, ставящую в соответствие каждому
значение
, то для вычисления выражения
,
в которое входят и аппликация и абстракция, необходимо выполнить подстановку числа 3 в терм вместо переменной
. В результате получается
. Это соображение в общем виде записывается как
и носит название β-редукция. Выражение вида , то есть применение абстракции к некому терму, называется редексом (redex). Несмотря на то, что β-редукция по сути является единственной «существенной» аксиомой λ-исчисления, она приводит к весьма содержательной и сложной теории. Вместе с ней λ-исчисление обладает свойством полноты по Тьюрингу и, следовательно, представляет собой простейший язык программирования.
-преобразование выражает ту идею, что две функции являются идентичными тогда и только тогда, когда, будучи примененными к любому аргументу, дают одинаковые результаты.
-преобразование переводит друг в друга формулы
и
(только если
не имеет свободных вхождений в {\displaystyle f}
: иначе, свободная переменная
после преобразования станет связанной внешней абстракцией или наоборот).
Синтаксис ζ-исчисления
| b ::= | термы: |
| x | переменная |
| [li = ζ(xi)bi] | объекты |
| b.l | вызов метода |
| b1.l⇐ ζ(x)b2 | замена метода |
| clone(b) | клонирование |
| let x=b1 in b2 | локальное объявление |
-исчисление в теоретической информатике — исчисление процессов, изначально разработанное Робином Милнером, Иоахимом Парровом и Дэвидом Уолкером как продолжение работы над исчислением общающихся систем. Целью
-исчисления является возможность описать параллельные вычисления, конфигурация которых может меняться на протяжении вычисления.
-исчисление принадлежит к семейству исчислений процессов. Фактически {\displaystyle \pi }
-исчисление как λ-исчисление настолько минимально, что не содержит примитивов, таких как числа, булевы выражения, структуры данных, переменные, функции или операторы управления потоком (например, if-then-else, while).
Синтаксис π-исчисления
| P, Q, R ::= | термы: |
| 0 | бездействующий процесс |
| x(y).P | получение y из канала x и выполнение P |
| xy.P | отправка y в канал x и выполнение P |
| P|Q | параллельное выполнение |
| (νx)P | создание канала |
| !P | репликация |
Операционная семантика описывает последовательный процесс смены состояний — абстрактная машина.
Полиморфизм — это использование одного фрагмента программы с разными типами в разных контекстах.
Виды полиморфизма
Существует множество различных теорий множеств и множество различных систем теории типов, поэтому все, что следует ниже, является обобщением.
Хотя первоначальная мотивация теории категорий была далека от фундаментализма, оказалось, что эти две области имеют глубокую связь. Как пишет Джон Лейн Белл : «Фактически категории сами по себе могут рассматриваться как теории типов определенного вида; один этот факт указывает на то, что теория типов гораздо более тесно связана с теорией категорий, чем с теорией множеств». Короче говоря, категорию можно рассматривать как теорию типов, рассматривая ее объекты как типы (или сорта), т.е. «грубо говоря, категорию можно рассматривать как теорию типов, лишенную своего синтаксиса». Таким образом, следует ряд важных результатов:
Взаимодействие, известное как категориальная логика , с тех пор стало предметом активных исследований; см., например, монографию Джейкобса (1999).
Исследование, описанное в статье про теория типов, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое теория типов, базовые вычислительные формализмы, семантические стили, вычислительные формализмы и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Структуры данных
Комментарии
Оставить комментарий
Структуры данных
Термины: Структуры данных