Список систем счисления, виды чисел

Привет, Вы узнаете о том , что такое числа, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое числа , настоятельно рекомендую прочитать все из категории Арифметика.

Существует много различных систем счисления , то есть систем письма для выражения чисел .

Система счисления — это система записи чисел , то есть математическая запись для представления чисел заданного набора с использованием цифр или других символов последовательным образом.

Одна и та же последовательность символов может представлять разные числа в разных системах счисления. Например, «11» обозначает число одиннадцать в десятичной системе счисления (наиболее распространенной сегодня в мире), число три в двоичной системе счисления (используемой в современных компьютерах) и число два в унарной системе счисления (используемой при подсчете очков).

Число, которое представляет цифра, называется ее значением . Кроме того, не все системы счисления могут представлять один и тот же набор чисел; например, в римских , греческих и египетских цифрах нет официального представления числа ноль .

В идеале система счисления должна:

• Представлять полезный набор чисел (например, все целые числа или рациональные числа )
• Дайте каждому представленному числу уникальное представление (или, по крайней мере, стандартное представление).
• Отражать алгебраическую и арифметическую структуру чисел.

Например, обычное десятичное представление дает каждому ненулевому натуральному числу уникальное представление в виде конечной последовательности цифр, начиная с ненулевой цифры.

Системы счисления иногда называют системами счисления , но это название неоднозначно, поскольку оно может относиться к разным системам чисел, например, к системе действительных чисел , системе комплексных чисел , различным гиперкомплексным системам счисления, системе p -адических чисел и т. д. Такие системы, однако, не являются темой данной статьи.

Система письма включает в себя набор символов , называемый письменностью , а также правила, по которым эта письменность представляет собой конкретный язык . Первые письменности появились в конце IV тысячелетия до нашей эры. На протяжении истории каждая независимо созданная система письма постепенно развивалась из системы протописьма , в которой использовалось небольшое количество иероглифов, неспособных полностью кодировать язык и, следовательно, выражать широкий спектр идей.

Системы письма обычно классифицируются в соответствии с тем, как их символы, называемые графемами , соотносятся с единицами языка. Фонетические системы письма, которые включают алфавиты и слоговые азбуки , используют графемы, которые соответствуют звукам в соответствующем разговорном языке . Алфавиты используют графемы, называемые буквами , которые обычно соответствуют произносимым фонемам . Они обычно делятся на три подтипа: Чистые алфавиты используют буквы для представления как согласных, так и гласных звуков, абджады обычно используют только буквы, представляющие согласные звуки, а абугиды используют буквы, представляющие пары согласная-гласная. Слоговые азбуки используют графемы, называемые силлабограммами , которые представляют целые слоги или моры . Напротив, логографические (или морфографические ) системы письма используют графемы, которые представляют единицы значения в языке, такие как его слова или морфемы . Алфавиты обычно используют менее 100 различных символов, в то время как силлабарии и логографии могут использовать сотни или тысячи соответственно.

Числа можно классифицировать в зависимости от способа их представления или в зависимости от свойств, которыми они обладают.

• Натуральные числа ( ): Числа, используемые для счета, {1, 2, 3, ...} обычно называются натуральными числами; однако другие определения включают 0, поэтому неотрицательные целые числа {0, 1, 2, 3, ...} также называются натуральными числами. Натуральные числа, включая 0, иногда называются целыми числами . В качестве альтернативы, натуральные числа, не включающие 0, иногда также называются целыми числами .
• Целые числа ( ): Положительные и отрицательные числительные, а также ноль: {..., −3, −2, −1, 0, 1, 2, 3, ...}.
• Рациональные числа ( ): числа, которые можно выразить как отношение целого числа к целому числу, отличному от нуля. Все целые числа рациональны, но существуют рациональные числа, которые не являются целыми, например, −2/9 .
• Действительные числа ( ): числа, соответствующие точкам на прямой. Они могут быть положительными, отрицательными или равными нулю. Все рациональные числа действительны, но обратное неверно.
• Иррациональные числа ): Действительные числа, которые не являются рациональными.
• Мнимые числа : числа, равные произведению действительного числа на мнимую единицу.я, гдея2=−1Число 0 является как действительным, так и мнимым.
• Комплексные числа ( ): Включает действительные числа, мнимые числа, а также суммы и разности действительных и мнимых чисел.
• Гиперкомплексные числа включают в себя различные расширения числовых систем: кватернионы ( ), октонионы ( ), седенионы ( ), тригинтадуонионы ( ) и другие гиперкомплексные числа размерности 64 и выше. Менее распространенные варианты включают в себя бикомплексные числа , кокватернионы и бикватернионы .
• p -адические числа : различные числовые системы, построенные с использованием пределов рациональных чисел, в соответствии с понятием «предела», отличным от того, которое используется для построения действительных чисел.

• Десятичная система : стандартная индо-арабская система счисления, использующая основание десять.
• Двоичная система : система счисления с основанием 2, используемая в компьютерах, с цифрами 0 и 1.
• Троичная система счисления : система счисления с основанием 3, в которой используются цифры 0, 1 и 2.
• Кватернарная система : система счисления с основанием четыре, в которой используются цифры 0, 1, 2 и 3.
• Шестнадцатеричная система счисления : основание 16, широко используется проектировщиками и программистами компьютерных систем, поскольку обеспечивает более удобное для человека представление двоично-кодированных значений.
• Восьмеричная система счисления : основание 8, иногда используется проектировщиками компьютерных систем и программистами.
• Двенадцатеричная система : основание 12, система счисления, удобная из-за множества множителей числа 12.
• Шестидесятеричная система счисления : основание 60, впервые использованное древними шумерами в 3-м тысячелетии до н. э., перешло к древним вавилонянам.
• Информацию о других базах см . в позиционной нотации .
• Римские цифры : система счисления Древнего Рима , которая иногда используется и сегодня, в основном в ситуациях, не требующих арифметических действий.
• Метки счета : Обычно используются для подсчета вещей, которые увеличиваются на небольшие величины и не изменяются очень быстро.
• Дроби : представление нецелого числа в виде отношения двух целых чисел. К ним относятся неправильные дроби , а также смешанные числа .
• Цепная дробь : выражение, полученное с помощью итеративного процесса представления числа в виде суммы его целой части и обратной ему величины другого числа, затем записи этого другого числа в виде суммы его целой части и другой обратной ему величины и т. д.
• Научная запись : метод записи очень малых и очень больших чисел с использованием степеней числа 10. При использовании в науке такое число также передает точность измерения с помощью значащих цифр .
• Нотация Кнута со стрелкой вверх и нотация Конвея с цепочкой стрелок : нотации, которые позволяют кратко представить некоторые чрезвычайно большие целые числа, такие как число Грэма .

• Положительные числа : действительные числа, которые больше нуля.
• Отрицательные числа : действительные числа, меньшие нуля. Поскольку сам ноль не имеет знака , ни положительные, ни отрицательные числа не включают ноль. Когда существует вероятность нуля, часто используются следующие термины:
• Неотрицательные числа: действительные числа, которые больше или равны нулю. Таким образом, неотрицательное число — это либо ноль, либо положительное число.
• Неположительные числа: действительные числа, которые меньше или равны нулю. Таким образом, неположительное число — это либо ноль, либо отрицательное число.

• Четные и нечетные числа : целое число является четным, если оно кратно 2, и нечетным в противном случае.
• Простое число : положительное целое число, имеющее ровно два положительных делителя : себя и 1. Простые числа образуют бесконечную последовательность 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, ...
• Составное число : положительное целое число, которое можно разложить на множители, состоящие из меньших положительных целых чисел. Каждое целое число, большее единицы, является либо простым, либо составным.
• Многоугольные числа : это числа, которые можно представить в виде точек, расположенных в форме правильного многоугольника , включая треугольные числа , квадратные числа , пятиугольные числа , шестиугольные числа , семиугольные числа , восьмиугольные числа, девятиугольные числа , десятиугольные числа , одиннадцатиугольные числа и двенадцатиугольные числа .
• Существует множество других известных целочисленных последовательностей , таких как последовательность чисел Фибоначчи , последовательность чисел Люка , последовательность факториалов , последовательность совершенных чисел и т. д., многие из которых перечислены в Онлайновой энциклопедии целочисленных последовательностей .

• Алгебраическое число : любое число, являющееся корнем ненулевого многочлена с рациональными коэффициентами .
• Трансцендентное число : любое действительное или комплексное число, не являющееся алгебраическим. Примеры включают e и π .
• Тригонометрическое число : любое число, являющееся синусом или косинусом рационального кратного числа π .
• Квадратное иррациональное уравнение : корень квадратного уравнения с рациональными коэффициентами. Такое число является алгебраическим и может быть выражено как сумма рационального числа и квадратного корня рационального числа.
• Построенное число : число, представляющее собой длину, которую можно построить с помощью циркуля и линейки . Построенные числа образуют подполе области алгебраических чисел и включают в себя квадратные иррациональные числа.
• Алгебраическое целое число : корень монома с целыми коэффициентами.

• Трансфинитные числа : числа, которые больше любого натурального числа.
• Порядковые числа : конечные и бесконечные числа, используемые для описания типа порядка вполне упорядоченных множеств .
• Кардинальные числа : конечные и бесконечные числа, используемые для описания мощностей множеств .
• Бесконечно малые : они меньше любого положительного действительного числа, но, тем не менее, больше нуля. Они использовались на начальном этапе развития математического анализа и применяются в синтетической дифференциальной геометрии .
• Гипердействительные числа : числа, используемые в нестандартном анализе . К ним относятся бесконечные и бесконечно малые числа, обладающие некоторыми свойствами действительных чисел.
• Сюрреалистические числа : числовая система, включающая в себя гиперреальные числа, а также порядковые.
• Нечеткие числа : обобщение действительных чисел, в котором каждый элемент представляет собой связанный набор возможных значений с весами.

• Вычислимое число : Действительное число, цифры которого можно вычислить с помощью некоторого алгоритма .
• Период : число, которое можно вычислить как интеграл некоторой алгебраической функции по алгебраической области .
• Определимое число : Действительное число, которое можно определить однозначно с помощью формулы первого порядка с одной свободной переменной на языке теории множеств .

" Основание — это натуральное число B, степени которого (B, умноженное само на себя определенное количество раз) особым образом обозначены в числовой системе".   Этот термин не эквивалентен основанию , поскольку он применяется ко всем числовым системам записи (не только к позиционным с основанием) и к большинству систем устных чисел. В некоторых системах есть два основания: меньшее (подоснование) и большее (основание); примером служат римские цифры, которые организованы по пятеркам (V=5, L=50, D=500, подоснование) и десяткам (X=10, C=100, M=1000, основание).

Имя	База	Образец	Примерное первое появление
Протоклинописные цифры	10 и 60		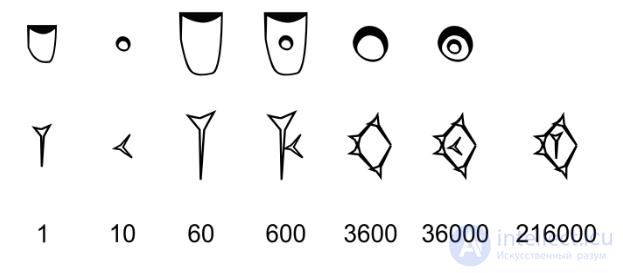ок. Об этом говорит сайт https://intellect.icu . 3500–2000 гг. до н.э.
долины Инда цифры	неизвестно	не дешифровано, предложен ряд гипотез	ок. 3500–1900 гг. до н.э.
Протоэламские цифры	10 и 60	не расшифровано	3100 г. до н.э.
Шумерские цифры	10 и 60		3100 г. до н.э.
египетские цифры	10		3000 г. до н.э.
Вавилонские цифры	10 и 60		2000 г. до н.э.
Эгейские цифры	10		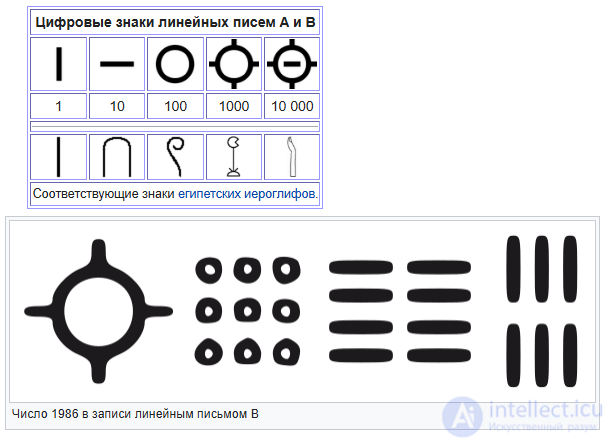1500 г. до н.э.
Китайские цифры Японские цифры Корейские цифры ( китайско-корейские ) Вьетнамские цифры ( китайско-вьетнамские )	10	零一二三四五六七八九十百千萬億 (по умолчанию, традиционный китайский ) 〇一二三四五六七八九十百千万亿 (по умолчанию, упрощенный китайский )	1300 г. до н.э.
римские цифры	5 и 10	IVXLCDM	1000 г. до н.э. [ 1 ]
Еврейские цифры	10	א ב ג ד ה ו ז ח ט י כ ל מ נ ס ע פ צ ק ר ש ת ך ם ן ף ץ	800 г. до н.э.
Индийские цифры	10	Bengali ০ ১ ২ ৩ ৪ ৫ ৬ ৭ ৮ ৯ Devanagari ० १ २ ३ ४ ५ ६ ७ ८ ९ Gujarati ૦ ૧ ૨ ૩ ૪ ૫ ૬ ૭ ૮ ૯ Kannada ೦ ೧ ೨ ೩ ೪ ೫ ೬ ೭ ೮ ೯ Malayalam ൦ ൧ ൨ ൩ ൪ ൫ ൬ ൭ ൮ ൯ Odia ୦ ୧ ୨ ୩ ୪ ୫ ୬ ୭ ୮ ୯ Punjabi ੦ ੧ ੨ ੩ ੪ ੫ ੬ ੭ ੮ ੯ Tamil ௦ ௧ ௨ ௩ ௪ ௫ ௬ ௭ ௮ ௯ Telugu ౦ ౧ ౨ ౩ ౪ ౫ ౬ ౭ ౮ ౯ Tibetan ༠ ༡ ༢ ༣ ༤ ༥ ༦ ༧ ༨ ༩ Urdu ۰ ۱ ۲ ۳ ۴ ۵ ۶ ۷ ۸ ۹	750–500 до н.э.
Греческие цифры	10	ō α β γ δ ε ϝ ζ η θ ι ο Α' Β' Γ' Δ' Ε' Ϛ' Ζ' Η' Θ'	<400 г. до н.э.
Цифры кхароштхи	4 и 10	𐩇 𐩆 𐩅 𐩄 𐩃 𐩂 𐩁 𐩀	<400–250 до н.э. [ 3 ]
финикийские цифры	10	𐤙 𐤘 𐤗 𐤛𐤛𐤛 𐤛𐤛𐤚 𐤛𐤛𐤖 𐤛𐤛 𐤛𐤚 𐤛𐤖 𐤛 𐤚 𐤖	<250 г. до н.э. [ 5 ]
Китайские стержневые цифры	10	Да, мы есть	1-й век
Коптские цифры	10	Ⲁ Ⲃ Ⲅ Ⲇ Ⲉ Ⲋ Ⲍ Ⲏ Ⲑ	2-й век
Цифры геэз	10	፩ ፪ ፫ ፬ ፭ ፮ ፯ ፰ ፱ ፲ ፳ ፴ ፵ ፶ ፷ ፸ ፹ ፺ ፻ ፼	3–4 века 15 века (современный стиль) [ 7 ] : 135–136
Армянские цифры	10	Ա Բ Գ Դ Ե Զ Է Ը Թ Ժ	Начало V века
Кхмерские цифры	10	០ ១ ២ ៣ ៤ ៥ ៦ ៧ ៨ ៩	Начало VII века
тайские цифры	10	๐ ๑ ๒ ๓ ๔ ๕ ๖ ๗ ๘ ๙	7-й век [ 8 ]
Числа абджада	10	غ ظ ض ذ خ ث ت ش ر ق ص ف ع س ن م ل ك ي ط ح ز و هـ د ج ب ا	<8-го века
Китайские цифры (финансовые)	10	零壹貳參肆伍陸柒捌玖拾佰仟萬億 (тихоокеанский китайский) 零壹贰叁肆伍陆柒捌玖拾佰仟萬億 (южнокитайский)	конец 7-го/начало 8-го века [ 9 ]
Восточные арабские цифры	10	٩ ٨ ٧ ٦ ٥ ٤ ٣ ٢ ١ ٠	8-й век
Вьетнамские цифры ( Chữ Nôm )	10	𠬠 𠄩 𠀧 𦊚 𠄼 𦒹 𦉱 𠔭 𠃩	<9-го века
Западные арабские цифры	10	0 1 2 3 4 5 6 7 8 9	9 век
Глаголические цифры	10	Ⰰ Ⰱ Ⰲ Ⰳ Ⰴ Ⰵ Ⰶ Ⰷ Ⰸ ...	9 век
Кириллические цифры	10	а в г д е е з и й...	10 век
Цифры Руми	10		10 век
бирманские цифры	10	၀ ၁ ၂ ၃ ၄ ၅ ၆ ၇ ၈ ၉	11 век [ 10 ]
Тангутские числительные	10		11 век (1036)
Цистерцианские цифры	10		13 век
Цифры майя	5 и 20		<15 век
Числа Муиска	20		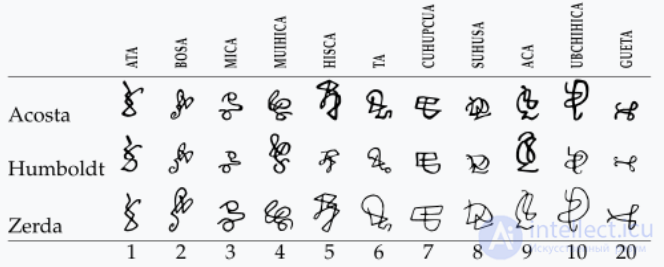<15 век
Корейские цифры ( хангыль )	10	영 일 이 삼 사 오 육 칠 팔 구	15 век (1443)
Ацтекские цифры	20		16 век
Сингальские цифры	10	෦ ෧ ෨ ෩ ෪ ෫ ෬ ෭ ෮ ෯ 𑇡 𑇢 𑇣 𑇤 𑇥 𑇦 𑇧 𑇨 𑇩 𑇪 𑇫 𑇬 𑇭 𑇮 𑇯 𑇰 𑇱 𑇲 𑇳 𑇴	<18 век
Пентадические руны	10		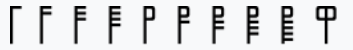19 век
Цифры чероки	10		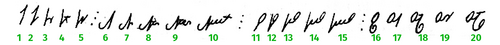XIX век (1820-е годы)
Цифры Ваи	10	꘠ ꘡ ꘢ ꘣ ꘤ ꘥ ꘦ ꘧ ꘨ ꘩	19 век (1832)
Цифры Бамум	10		19 век (1896)
Цифры Менде Кикакуи	10		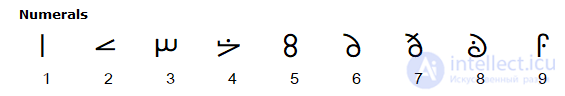20 век (1917)
Османские цифры	10		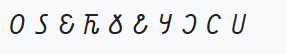20-й век (1920-е годы)
Цифры Медефаидрина	20		20-й век (1930-е годы)
Цифры Н'Ко	10		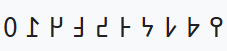20-й век (1949) [ 19 ]
Числительные хмонг	10		20 век (1959)
Цифры Гарая	10		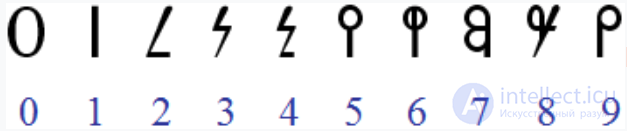20-й век (1961)
Цифры Адлама	10		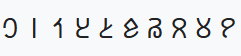20-й век (1989)
Кактовиковые цифры	5 и 20		20-й век (1994)
Суданские цифры	10		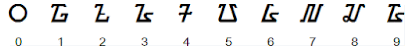20-й век (1996)

Системы счисления классифицируются здесь в зависимости от того, используют ли они позиционную систему счисления (также известную как разрядная система счисления), а также по основанию .

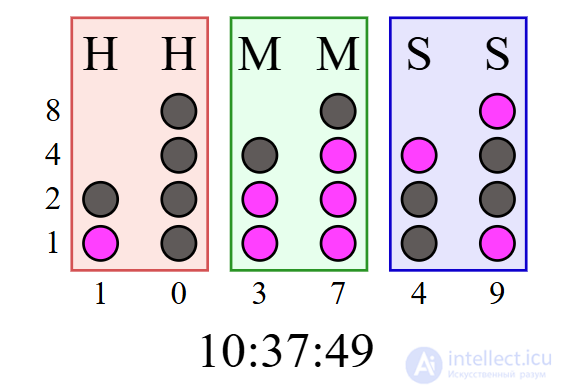
В двоичных часах светодиоды могут использоваться для отображения двоичных значений. В таких часах каждый столбец светодиодов отображает двоично-десятичное число традиционного шестидесятеричного времени.

Распространенные названия происходят отчасти произвольно, из смеси латинского и греческого , в некоторых случаях включая корни из обоих языков в одном названии. Были некоторые предложения по стандартизации.

База	Имя	Использование
2 я	Четвертная мнимая база	связанные с основанием −4 и основанием 16
	Базая2	связанные с основанием −2 и основанием 4
	Базая24	связанный с основанием 2
	База2ω	связанный с основанием 8
	Базаω23	связанный с основанием 2
−1 ± i	База Твиндрагон	Фрактальная форма Twindragon , связанная с основанием −4 и основанием 16
1 ± i	База Негатвиндрагона	связанные с основанием −4 и основанием 16

База	Имя	Использование
	База32	рациональное нецелое основание
	База43	связанный с двенадцатеричным
	База52	связанный с десятичной дробью
	База2	связанный с основанием 2
	База3	связанный с основанием 3
	База23
	База24
	База212	использование в 12-тоновой равномерно темперированной музыкальной системе
	База22
	База−32	отрицательное рациональное нецелое основание
	База−2	отрицательное нецелое основание, связанное с основанием 2
	База10	связанный с десятичной дробью
	База23	связанный с двенадцатеричным
φ	Золотое сечение	ранний бета-кодер
ρ	Пластиковая подставка под номер
ψ	База суперзолотого сечения
	База серебряного коэффициента
е	Базае	лучшая экономика счисления
π	Базаπ
е π	Базаеπ
еπ	Базаеπ

• Факториальная система счисления {1, 2, 3, 4, 5, 6, ...}
• Четная двухфакторная система счисления {2, 4, 6, 8, 10, 12, ...}
• Нечетная двухфакторная система счисления {1, 3, 5, 7, 9, 11, ...}
• Первичная система счисления {2, 3, 5, 7, 11, 13, ...}
• Фибонорная система счисления {1, 2, 3, 5, 8, 13, ...}
• {60, 60, 24, 7} в хронометраже
• {60, 60, 24, 30 (или 31 или 28 или 29), 12, 10, 10, 10} в хронометраже
• (12, 20) традиционная английская денежная система (£sd)
• (20, 18, 13) Майяское летоисчисление

• Обозначение кавычек
• Избыточное двоичное представление
• Наследственная система счисления с основанием n
• Асимметричные системы счисления , оптимизированные для неравномерного распределения вероятностей символов
• Комбинаторная система счисления

Все известные системы счисления, разработанные до вавилонских цифр, являются непозиционными, как и многие, разработанные позже, например, римские цифры . Французские монахи-цистерцианцы создали свою собственную систему счисления.

Исследование, описанное в статье про числа, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое числа и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Арифметика