Практика
В мире разработки программного обеспечения, эффективность выполнения запросов к базе данных играет ключевую роль в обеспечении быстродействия приложений. В этом контексте понимание сложности алгоритма (Big O notation) при выборке данных из базы данных с использованием SQL становится важным аспектом для разработчиков и архитекторов систем. Сложность алгоритма в SQL зависит от различных факторов, таких как наличие индексов, структура запроса, объем данных и другие аспекты, оказывающие влияние на производительность. В данной статье мы рассмотрим ключевые аспекты сложности алгоритма при выборке данных в SQL, и как оптимизация запросов может существенно повлиять на производительность базы данных и, следовательно, на работу приложений.
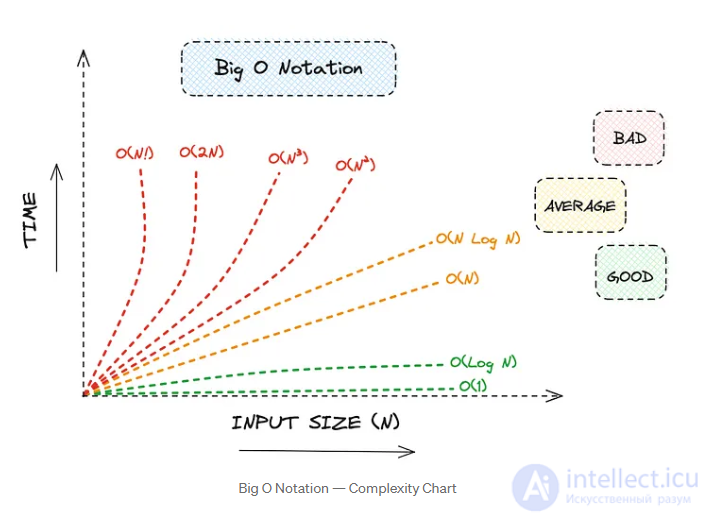
В контексте SQL и выборки данных из базы данных, оценка сложности алгоритма с использованием нотации Big O является ключевым моментом для оптимизации производительности запросов. Big O notation предоставляет абстрактное представление о том, как рост объема данных влияет на производительность алгоритма. Рассмотрим некоторые особенности этой нотации в контексте SQL-запросов.
O(1) - Константная сложность:
O(log N) - Логарифмическая сложность:
O(N) - Линейная сложность:
O(N log N) - Линейно-логарифмическая сложность:
O(N^2) и выше - Квадратичная сложность и выше:
При многократных соединениях в SQL запросе сложность алгоритма (Big O notation) зависит от конкретной структуры запроса, наличия индексов и объема данных. Давайте рассмотрим несколько случаев:
Последовательные соединения (Nested Loop Join):
Соединения с использованием хешей (Hash Join):
Сортировка перед соединением (Sort-Merge Join):
Использование индексов в JOIN:
Множественные соединения JOIN ... JOIN :
Важно отметить, что производительность запросов в значительной степени зависит от правильного использования индексов, наличия статистики, оптимизатора запросов и общей структуры базы данных. В различных СУБД и сценариях производительность может сильно варьироваться.
Оптимизация запросов включает в себя использование индексов, правильное проектирование базы данных, написание эффективных запросов и использование кэширования. Понимание сложности алгоритма в контексте SQL помогает разработчикам сделать информированные решения для обеспечения высокой производительности базы данных в рамках их приложений.
С линейным временем выполнения тесно связано время выполнения планов, имеющих соединения таблиц. Вот несколько примеров:
Если выполняется запрос SELECT * FROM table без использования индекса, то сложность алгоритма может быть оценена как O(N), где N - количество записей в таблице.
В данном случае, база данных должна просмотреть все строки таблицы для удовлетворения запроса SELECT * FROM table. Это означает, что время выполнения запроса будет пропорционально количеству записей в таблице.
Использование индексов может значительно ускорить процесс выборки данных, так как индексы предоставляют структурированный способ поиска конкретных значений. Однако, если индексы не используются, база данных вынуждена просматривать все строки, что может быть ресурсозатратным для больших таблиц.
Если вы выполняете запрос вида SELECT * FROM table WHERE id=N и в таблице есть индекс на столбец id, то сложность алгоритма будет O(log N), где N - количество записей в таблице.
Использование индекса на столбец id позволяет базе данных эффективно находить нужную запись, применяя бинарный поиск. В результате выполнения такого запроса будет выполнен быстрый и эффективный поиск по индексу, что дает логарифмическую сложность.
Важно отметить, что O(log N) возможно при использовании сбалансированных структур данных для индексов, таких как B-деревья или B+деревья, которые обеспечивают эффективный поиск в отсортированных данных.
Если выполняется запрос вида SELECT * FROM table1 LEFT JOIN table2 ON table1.f = table2.f, и при этом не используется индекс для соединения (ON table1.f = table2.f), то сложность алгоритма будет O(M * N), где M - количество записей в table1, а N - количество записей в table2.
Без использования индекса для соединения, база данных должна выполнить "вложенный цикл" (nested loop) или "строитель хеш-таблицы" (hash build) для объединения записей из table1 и table2. В этом случае каждая запись из table1 будет проверяться на соответствие каждой записи из table2, что приводит к квадратичной сложности.
Использование индекса для соединения могло бы значительно ускорить процесс, уменьшив сложность до O(M * log N) или O(M + N) в зависимости от конкретного типа индекса и оптимизаций, применяемых базой данных.
Комментарии
Оставить комментарий
Базы данных, знаний и хранилища данных. Big data, СУБД и SQL и noSQL
Термины: Базы данных, знаний и хранилища данных. Big data, СУБД и SQL и noSQL