Лекция
Привет, Вы узнаете о том , что такое реляционные соединения, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое реляционные соединения, операции над отношениями, реляционная алгебра , настоятельно рекомендую прочитать все из категории Базы данных, знаний и хранилища данных. Big data, СУБД и SQL и noSQL.
реляционная алгебра — это теоретический язык операций, позволяющих создавать на основе одного или нескольких отношений другое отношение без изменения самих исходных отношений. Таким образом, оба операнда и результат являются отношениями, поэтому результаты одной операции могут применяться в другой операции. Это позволяет создавать вложенные выражения реляционной алгебры (по аналогии с тем, как создаются вложенные арифметические выражения), но при любой глубине вложенности результатом является отношение. Такое свойство называется замкнутостью. Оно подчеркивает то, что применение любого количества операций реляционной алгебры к отношениям не приводит к созданию иных объектов, кроме отношений, точно так же, как результатами арифметических операций с числами являются только числа.
Реляционная алгебра является языком последовательного использования отношений, в котором все кортежи, возможно, даже взятые из разных отношений, обрабатываются одной командой, без организации циклов. Для команд реляционной алгебры предложено несколько вариантов синтаксиса. Ниже мы воспользуемся общепринятыми символическими обозначениями для этих команд и представим их в неформальном виде.
Замечание и Недостатки реляционнной алгебры
По справедливому замечанию Дейта, реляционная алгебра Кодда обладает несколькими недостатками:
Во-первых, восемь перечисленных операций по охвату своих функций, с одной стороны, избыточны, так как минимально необходимый набор составляют пять операций: объединение, вычитание, произведение, проекция и выборка. Три другие операции (пересечение, соединение и деление) можно определить через пять минимально необходимых.Так, например, соединение — это проекция выборки произведения.
Во-вторых, этих восьми операций недостаточно для построения реальной СУБД на принципах реляционной алгебры. Требуются расширения, включающие операции: переименования атрибутов, образования новых вычисляемых атрибутов, вычисления итоговых функций, построения сложных алгебраических выражений, присвоения, сравнения и т. д.
Рассмотрим основные операции над отношениями , которые могут представлять интерес с точки зрения извлечения данных из реляционных таблиц. Это объединение, пересечение, разность, расширенное декартово произведение отношений, а также специальные операции над отношениями: выборка, проекция и соединение.
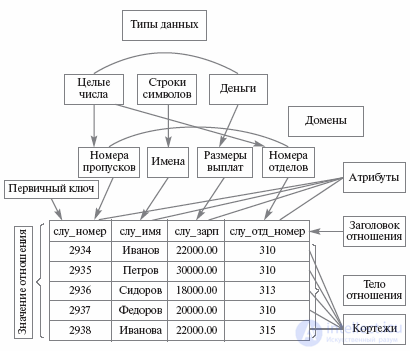
Для иллюстрации теоретико-множественных операций над отношениями введем абстрактные отношения (таблицы) с некоторыми атрибутами (полями).
| Отношение R | |
|---|---|
| R.a1 | R.a2 |
| A | 1 |
| A | 2 |
| B | 1 |
| B | 3 |
| B | 4 |
CREATE TABLE R (a1 CHAR(1), a2 INT, PRIMARY KEY(a1,a2))
| Отношение S | |
|---|---|
| S.b1 | S.b2 |
| 1 | h |
| 2 | g |
| 3 | h |
CREATE TABLE S (b1 INT PRIMARY KEY, b2 CHAR(1))
Операции выборки и проекции являются унарными, поскольку они работают с одним отношением.
Операция выборки - построение горизонтального подмножества, т.е. подмножества кортежей, обладающих заданными свойствами.
Операция выборки работает с одним отношением R и определяет результирующее отношение, которое содержит только те кортежи (строки) отношения R, которые удовлетворяют заданному условию F (предикату).
.
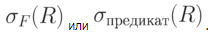Пример 5.1. Операция выборки в SQL.
Выборка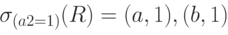 
записывается следующим образом:
SELECT a1, a2 FROM R WHERE a2=1
Операция проекции - построение вертикального подмножества отношения, т.е. подмножества кортежей, получаемого выбором одних и исключением других атрибутов.
Операция проекции работает с одним отношением R и определяет новое отношение, которое содержит вертикальное подмножествоотношения R, создаваемое посредством извлечения значений указанных атрибутов и исключения из результата строк-дубликатов.
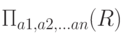
Пример 5.2. Операция проекции в SQL.
Проекция 
записывается следующим образом:
SELECT DISTINCT b2 FROM S
К основным операциям над отношениями относится декартово произведение.
Декартово произведение RxS двух отношений (двух таблиц) определяет новое отношение - результат конкатенации (т.е. сцепления) каждого кортежа (каждой записи) из отношения R с каждым кортежем (каждой записью) из отношения S .
RxS={(a, 1, 1, h), (a, 2, 1, h),
(b, 1, 1, h), ... }
SELECT R.a1, R.a2, S.b1, S.b2 FROM R, S
Результат декартова произведения двух отношений показан в таблице.
| R x S | |||
|---|---|---|---|
| R.a1 | R.a2 | S.b1 | S.b2 |
| a | 1 | 1 | h |
| a | 1 | 2 | g |
| a | 1 | 3 | h |
| a | 2 | 1 | h |
| a | 2 | 2 | g |
| a | 2 | 3 | h |
| b | 1 | 1 | h |
| b | 1 | 2 | g |
| b | 1 | 3 | h |
| b | 3 | 1 | h |
| b | 3 | 2 | g |
| b | 3 | 3 | h |
| b | 4 | 1 | h |
| b | 4 | 2 | g |
| b | 4 | 3 | h |
Если одно отношение имеет N записей и K полей, а другое M записей и L полей, то отношение с их декартовым произведением будет содержать NxM записей и K+L полей. Исходные отношения могут содержать поля с одинаковыми именами, тогда имена полей будут содержать названия таблиц в виде префиксов для обеспечения уникальности имен полей в отношении, полученном как результат выполнения декартова произведения.
Однако в таком виде (пример 5.3.) отношение содержит больше информации, чем обычно необходимо пользователю. Как правило, пользователей интересует лишь некоторая часть всех комбинаций записей в декартовом произведении, удовлетворяющая некоторому условию. Поэтому вместо декартова произведения обычно используется одна из самых важных операций реляционной алгебры - операциясоединения, которая является производной от операции декартова произведения. С точки зрения эффективности реализации в реляционныхСУБД эта операция - одна из самых трудных и часто входит в число основных причин, вызывающих свойственные всем реляционным системам проблемы с производительностью.
Соединение - это процесс, когда две или более таблицы объединяются в одну. Способность объединять информацию из нескольких таблиц или запросов в виде одного логического набора данных обусловливает широкие возможности SQL.
В языке SQL для задания типа соединения таблиц в логический набор записей, из которого будет выбираться необходимая информация, используется операция JOIN в предложении FROM.
Формат операции:
FROM имя_таблицы_1 {INNER | LEFT | RIGHT}
JOIN имя_таблицы_2
ON условие_соединения
Существуют различные типы операций соединения:
;
;
;
;
.
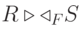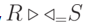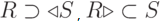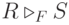Операция тета-соединения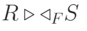 
определяет отношение, которое содержит кортежи из декартова произведения отношений R иS, удовлетворяющие предикату F. Предикат F имеет вид 
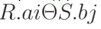, где вместо 
может быть указан один из операторов сравнения ( >, >=, <, <=, =, <> ).
Если предикат F содержит только оператор равенства ( = ), то соединение называется соединением по эквивалентности.
 |
|||
|---|---|---|---|
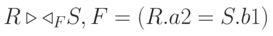| R.a1 | R.a2 | S.b1 | S.b2 |
| a | 1 | 1 | h |
| a | 2 | 2 | g |
| b | 3 | 3 | h |
| b | 1 | 1 | h |
Операция тета-соединения в языке SQL называется INNER JOIN (внутреннее соединение ) и используется, когда нужно включить все строки из обеих таблиц, удовлетворяющие условию объединения. Внутреннее соединение имеет место и тогда, когда в предложении WHEREсравниваются значения полей из разных таблиц. В этом случае строится декартово произведение строк первой и второй таблиц, а из полученного набора данных отбираются записи, удовлетворяющие условиям объединения.
В условиях объединения могут участвовать поля, относящиеся к одному и тому же типу данных и содержащие один и тот же вид данных, но они не обязательно должны иметь одинаковые имена.
Блоки данных из двух таблиц объединяются, как только в указанных полях будут найдены совпадающие значения.
Если в предложении FROM перечислено несколько таблиц и при этом не употребляется спецификация JOIN, а для указания соответствия полей из таблиц используется условие в предложении WHERE, то некоторые реляционные СУБД (например, Access) оптимизируют выполнение запроса, интерпретируя его как соединение.
Если перечислять ряд таблиц или запросов и не указывать условия объединения, в качестве исходной таблицы будет выбрано декартово (прямое) произведение всех таблиц.
SELECT R.a1, R.a2, S.b1, S.b2
FROM R, S
WHERE R.a2=S.b1
или
SELECT R.a1, R.a2, S.b1, S.b2
FROM R INNER JOIN S ON R.a2=S.b1
Естественное соединение
Естественным соединением называется соединение по эквивалентности двух отношений R и S, выполненное по всем общим атрибутам, из результатов которого исключается по одному экземпляру каждого общего атрибута.
 |
||
|---|---|---|
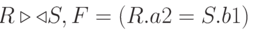| R.a1 | R.a2 или S.b1 | S.b2 |
| a | 1 | h |
| a | 2 | g |
| b | 3 | h |
| b | 1 | h |
SELECT R.a1, R.a2, S.b2
FROM R, S
WHERE R.a2=S.b1
или
SELECT R.a1, S.b1, S.b2
FROM R INNER JOIN S ON R.a2=S.b1
5.5. Естественное соединение отношений в SQL.
Пример 5.6. Вывести информацию о проданных товарах.
SELECT *
FROM Сделка, Товар
WHERE Сделка.КодТовара=Товар.КодТовара
Или (что эквивалентно)
SELECT *
FROM Товар INNER JOIN Сделка
ON Товар.КодТовара=Сделка.КодТовара
5.6. Выборка информации о проданных товарах.
Можно создать вложенные объединения, добавив третью таблицу к результату объединения двух других таблиц.
Пример 5.7. Получить сведения о товарах, дате сделок, количестве проданного товара и покупателях.
SELECT Товар.Название, Сделка.Количество, Сделка.
Дата, Клиент.Фирма
FROM Клиент INNER JOIN
(Товар INNER JOIN Сделка
ON Товар.КодТовара=Сделка.КодТовара)
ON Клиент.КодКлиента=Сделка.КодКлиента
Использование общих имен таблиц для идентификации столбцов неудобно из-за их громоздкости. Каждой таблице можно присвоить какое-нибудь краткое обозначение, псевдоним.
Пример 5.8. Получить сведения о товарах, дате сделок, количестве проданного товара и покупателях. В запросе используются псевдонимы таблиц.
SELECT Т.Название, С.Количество,
С.Дата, К.Фирма
FROM Клиент AS К INNER JOIN
(Товар AS Т INNER JOIN
Сделка AS С
ON Т.КодТовара=С.КодТовара)
ON К.КодКлиента=С.КодКлиента;
Внешнее соединение похоже на внутреннее, но в результирующий набор данных включаются также записи ведущей таблицы соединения, которые объединяются с пустым множеством записей другой таблицы.
Какая из таблиц будет ведущей, определяет вид соединения. LEFT - левое внешнее соединение, ведущей является таблица, расположенная слева от вида соединения ; RIGHT - правое внешнее соединение, ведущая таблица расположена справа от вида соединения.
Левое внешнее соединение
Левым внешним соединением называется соединение, при котором кортежи отношения R, не имеющие совпадающих значений в общих столбцах отношения S, также включаются в результирующее отношение.
 |
|||
|---|---|---|---|
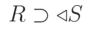| R.a1 | R.a2 | S.b1 | S.b2 |
| a | 1 | 1 | h |
| a | 2 | 2 | g |
| b | 1 | 1 | h |
| b | 3 | 3 | h |
| b | 4 | null | null |
SELECT R.a1, R.a2, S.b1, S.b2 FROM R LEFT JOIN S ON R.a2=S.b1
Существует и правое внешнее соединение 
, называемое так потому, что в результирующем отношении содержатся все кортежи правого отношения. Кроме того, имеется и полное внешнее соединение, в его результирующее отношение помещаются все кортежи из обоих отношений, а для обозначения несовпадающих значений кортежей в нем используются определители NULL.
SELECT R.a1, R.a2, S.b1, S.b2 FROM R RIGHT JOIN S ON R.a2=S.b1
Пример 5.11. Вывести информацию о всех товарах. Для проданных товаров будет указана дата сделки и количество. Для непроданных эти поля останутся пустыми.
SELECT Товар.*, Сделка.* FROM Товар LEFT JOIN Сделка ON Товар.КодТовара=Сделка.КодТовара;
Полусоединение
Операция полусоединения определяет отношение, содержащее те кортежи отношения R, которые входят в соединение отношений R иS .
 |
|
|---|---|
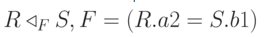| R.a1 | R.a2 |
| a | 1 |
| a | 2 |
| b | 3 |
| b | 1 |
SELECT R.a1, R.a2
FROM R, S
WHERE R.a2=S.b1
или
SELECT R.a1, R.a2
FROM R INNER JOIN S ON R.a2=S.b1
Объединение ( UNION ) 
отношений R и S можно получить в результате их конкатенации с образованием одного отношения с исключением кортежей-дубликатов. При этом отношения R и S должны быть совместимы, т.е. иметь одинаковое количество полей с совпадающими типами данных. Иначе говоря, отношения должны быть совместимы по объединению.
Объединением двух таблиц R и S является таблица, содержащая все строки, которые имеются в первой таблице R, во второй таблицеS или в обеих таблицах сразу.
SELECT R.a1, R.a2 FROM R UNION SELECT S.b2, S.b1 FROM S
Операция пересечения ( INTERSECT )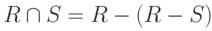 
определяет отношение, которое содержит кортежи, присутствующие как в отношении R, так и в отношении S. Отношения R и S должны быть совместимы по объединению .
Пересечением двух таблиц R и S является таблица, содержащая все строки, присутствующие в обеих исходных таблицах одновременно.
SELECT R.a1, R.a2
FROM R,S
WHERE R.a1=S.b1 AND R.a2=S.b2
или
SELECT R.a1, R.a2
FROM R
WHERE R.a1 IN
(SELECT S.b1 FROM S
WHERE S.b1=R.a1) AND R.a2 IN
(SELECT S.b2
FROM S
WHERE S.b2=R.a2)
Разность ( EXCEPT ) R-S двух отношений R и S состоит из кортежей, которые имеются в отношении R, но отсутствуют в отношенииS. Причем отношения R и S должны быть совместимы по объединению.
Разностью двух таблиц R и S является таблица, содержащая все строки, которые присутствуют в таблице R, но отсутствуют в таблицеS.
SELECT R.a1, R.a2
FROM R
WHERE NOT EXISTS
(SELECT S.b1,S.b2
FROM S
WHERE S.b1=R.a2 AND S.b2=R.a1)
Результат операции деления R:S - набор кортежей отношения R, определенных на множестве атрибутов C, которые соответствуют комбинации всех кортежей отношения S .
T1=П
C
( R ); T2=П
C
( (S X T1) -R ); T=T1 - T2.
Отношение R определено на множестве атрибутов A, а отношение S - на множестве атрибутов B, причем 
и C=A - B.
Пусть A ={имя, пол, рост, возраст, вес}; B ={имя, пол, возраст}; C ={рост, вес}.
| Отношение R | ||||
|---|---|---|---|---|
| имя | пол | рост | возраст | вес |
| a | ж | 160 | 20 | 60 |
| b | м | 180 | 30 | 70 |
| c | ж | 150 | 16 | 40 |
| Отношение S | ||
|---|---|---|
| имя | пол | возраст |
| a | ж | 20 |
| T1=ПC(R) | |
|---|---|
| рост | вес |
| 160 | 60 |
| 180 | 70 |
| 150 | 40 |
| TT=(S X T1)-R | ||||
|---|---|---|---|---|
| имя | пол | возраст | рост | вес |
| a | ж | 20 | 180 | 70 |
| a | ж | 20 | 150 | 40 |
| T2=ПC((S X T1)-R) | |
|---|---|
| рост | вес |
| 180 | 70 |
| 150 | 40 |
| T=T1-T2 | |
|---|---|
| рост | вес |
| 160 | 60 |
Пример 5.16. Деление отношений в SQL.
CREATE TABLE R (i int primary key, имя varchar(3), пол varchar(3), рост int, возраст int, вес int)5.16a. Деление отношений в SQL.
CREATE TABLE S (i int primary key, имя varchar(3), пол varchar(3), возраст int)5.16b. Деление отношений в SQL.
CREATE VIEW T1 AS SELECT рост,вес FROM R5.16c. Деление отношений в SQL.
CREATE VIEW TT AS
SELECT S.имя, S.пол, S.возраст,
T1.рост, T1.вес
FROM S, T1
5.16d. Деление отношений в SQL.
CREATE VIEW T2
AS
SELECT TT.рост, TT.вес
FROM TT
WHERE NOT EXISTS
(SELECT R.рост, R.вес
FROM R
WHERE TT.имя=R.имя AND TT.пол=R.пол
AND TT.возраст=R.возраст
AND TT.рост=R.рост
AND TT.вес=R.вес)
5.16e. Деление отношений в SQL.
SELECT T1.рост, T1.вес
FROM T1
WHERE NOT EXISTS
(SELECT T2.рост,T2.вес
FROM T2
WHERE T1.рост=T2.рост AND T1.вес=T2.вес)
5.16f. Деление отношений в SQL.
Таким образом , существует несколько вариантов выбора операций, которые включаются в реляционную алгебру. Первоначально Кодд предложил восемь операций, но впоследствии к ним были добавлены и некоторые другие. Пять основных операций реляционной алгебры, а именно
выполняют большинство действий по извлечению данных, которые могут представлять для нас интерес.
На основании пяти основных операций можно также вынести дополнительные операции, такие как операции
которые могут быть выражены в терминах пяти основных операций.
Операции выборки и проекции являются унарными, поскольку они работают с одним отношением. Другие операции работают с парами отношений, и поэтому их называют бинарными операциями. В приведенных ниже определениях R и S — это два отношения, определенные на атрибутах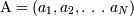 
и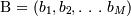 
соответственно.
Операция |
Обозначение |
Область применения |
Выборка |
 |
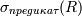Определяет результирующее отношение, которое содержит только те кортежи (строки) из отношения R, которые удовлетворяют заданному условию (предикату) |
Проекция |
 |
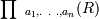Определяет новое отношение, содержащее вертикальное подмножество отношения R, создаваемое посредством извлечения значений указанных атрибутов и исключения из результата строк-дубликатов |
Объединение |
 |
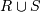Определяет новое отношение, которое включает все кортежи, содержащиеся только в R, только в S, одновременно в R и S, причем все дубликаты кортежей исключены. При этом отношения R и S должны быть совместимыми по объединению
|
Разность |
 |
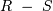Разность двух отношений R и s состоит из кортежей, которые имеются в отношении R. но отсутствуют в отношении S. Причем отношения R и s должны быть совместимыми по объединению |
Пересечение |
 |
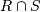Определяет отношение, которое содержит кортежи, присутствующие как в отношении R, так и в отношении S. Отношения R и S должны быть совместимыми по объединению |
Декартово произведение |
 |
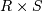Определяет новое отношение, которое является результатом конкатенации (т.е. сцепления) каждого кортежа из отношения R с каждым кортежем из отношения S |
Тета-cоединение |
 |
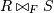Определяет отношение, которое содержит кортежи из декартова произведения отношений R и S, удовлетворяющие предикату F |
Соединение по эквивалентности |
|
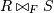Определяет отношение, которое содержит кортежи из декартова произведения отношений R и S, удовлетворяющие предикату F (предикат должен предусматривать только сравнение на равенство)
|
Естественное соединение |
 |
Естественным соединением называется соединение по эквивалентности двух отношений R и S, выполненное по всем общим атрибутам х, из результатов которого исключается по одному экземпляру каждого общего атрибута |
(Левое) внешнее соединение |
 |
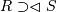Соединение, при котором кортежи отношения R, не имеющие совпадающих значений в общих столбцах отношения S, также включаются в результирующее отношение |
Полусоединение |
 |
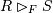Определяет отношение, содержащее те кортежи отношения R, которые входят в соединение отношений R и S |
Деление |
 |
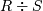Определяет отношение, состоящее из множества кортежей отношения R, которые определены на атрибуте С, соответствующем комбинации всех кортежей отношения S, где C — множество атрибутов, имеющихся в отношении R, но отсутствующих в отношении S |
Схематическое представление результатов операций реляционной алгебры
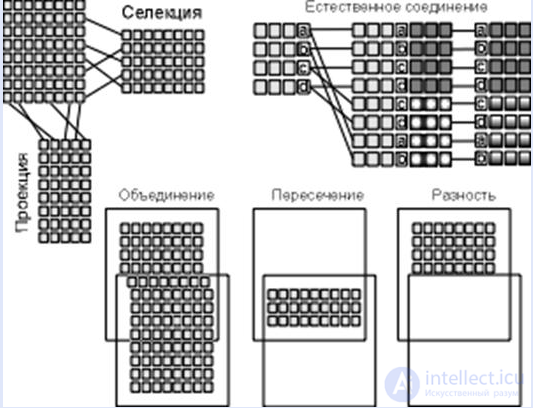
Некоторые операции реляционной алгебры
Созданы языки манипулирования данными, позволяющие реализовать все операции реляционной алгебры и практически любые их сочетания. Среди них наиболее распространены SQL (Structured Query Language – структуризованный язык запросов) и QBE (Quere-By-Example – запросы по образцу) . Оба относятся к языкам очень высокого уровня, с помощью которых пользователь указывает, какие данные необходимо получить, не уточняя процедуру их получения. С помощью единственного запроса на любом из этих языков можно соединить несколько таблиц во временную таблицу и вырезать из нее требуемые строки и столбцы (селекция и проекция).
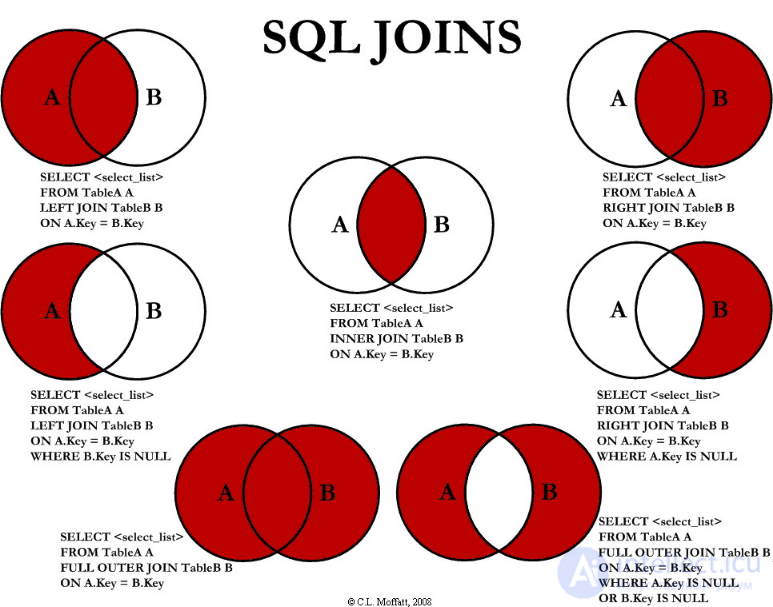
Использования Диаграммы Венна для объяснения джойнов. Но это НЕПРАВИЛЬНО!
Диаграммы Венна превосходно подходят для иллюстрации операций над множествами! В SQL известно три из них:
Операция JOIN намного полезней. Например, Вы хотите соединить набор актеров со связанным с ним набором фильмов.
JOIN на самом деле декартово произведение с фильтрами. Приведем хорошую иллюстрацию декартова произведения:
Так какой же лучший способ иллюстрировать операции JOIN?
Диаграммы JOINов! Давайте сперва глянем на CROSS JOIN. потому что дргуие типы JOIN могут быть выведены из CROSS JOIN:
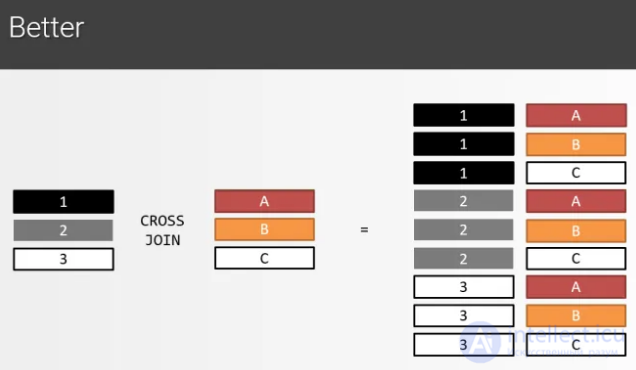
Запомните, перекрестное соединение (cross join) совершается следующим образом: берется каждый элемент из левой стороны, и соединяется с каждым элементом с правой стороны. Когда вы совершаете CROSS JOIN таблицы с 3 записями с таблицей, укоторой 4 записи, то получите 3×4=12 результирующих записей.
Все другие джойны базируются на перекрестном джойне, но с дополнительными фильтрами, и возможно объединениями. Приведем объяснение каждого типа JOIN.
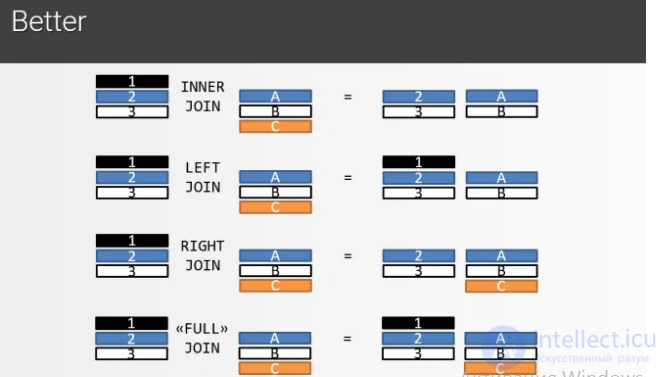
INNER JOIN это CROSS JOIN, в котором содержатся только те комбинации которые сохранились в соответствии с заданным предикатом.
Типы OUTER JOIN помогают нам, там где мы хотим оставить только те записи, либо с ЛЕВОЙ стороны, либо с ПРАВОЙ или с обоих (FULL) сторон, которые соответствуют предикату.
LEFT OUTER JOIN в реляционной алгебре определяются как:
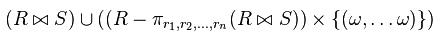
В SQL:
В результате мы получим всех авторов и их книги, но если автор не имеет ни одной книги, мы получим автора с NULL в качестве значения его книги. Это то же самое, что написать так:
Но никто не хочет писать столько SQL, поэтому OUTER JOIN были введены.
Есть следующие таблицы со значениями цветов:
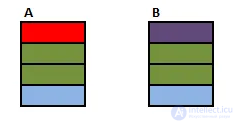
SELECT A.Colour, B.Colour FROM A CROSS JOIN B
Cross join (или декартово произведение) создает результат с каждой комбинацией записей с двух таблиц. Каждая таблица имеет по 4 записи и результат будет содержать 16 записей.
SELECT A.Colour, B.Colour FROM A INNER JOIN B ON A.Colour = B.Colour
Inner join вернет все записи из перекрестного соединения, которые соответствуют условию join. В этом случае имеем 5 записей:
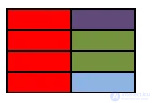
SELECT A.Colour, B.Colour FROM A INNER JOIN B ON A.Colour NOT IN (‘Green’,’Blue’)
Условие join не обязательно должно быть условием равенства и не всегда может иметь ссылки на столбцы из обоих (или даже одной) из таблиц. Вычисление условия A.Colour NOT IN ('Green','Blue') на каждой строке cross join возвращает:
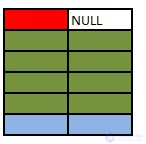
SELECT A.Colour, B.Colour FROM A LEFT OUTER JOIN B ON A.Colour = B.Colour
Outer join логически вычисляются таким же способом, как и inner джойны, кроме того что если запись из левой таблицы (или правой) не соединяется с любой из строк из правой таблицы она будет внесена в результат со значением NULL для правой колонки.
SELECT A.Colour, B.Colour FROM A LEFT OUTER JOIN B ON A.Colour = B.Colour WHERE B.Colour IS NULL
В этом примере просто ограничивается результат предыдущего примера, теперь результат возвращает записи, в которых B.Colour IS NULL. В этом конкретном случае, это будут строки, которые не имеют совпадений с правой стороны и запрос вернет единственную красную строку, которая не имеет совпадений с таблицей B. Этот трюк также известен как anti semi join.
SELECT A.Colour, B.Colour FROM A RIGHT OUTER JOIN B ON A.Colour = B.Colour
RIGHT OUTER JOIN действует так же, как и LEFT OUTER JOIN, кроме того, что он хранит не сопадающие записи с правой таблицы и NULL в качестве значения записи из левой таблицы.
SELECT A.Colour, B.Colour FROM A FULL OUTER JOIN B ON A.Colour = B.Colour
FULL OUTER JOIN комбинирует поведение левого и правого джойна и хранит не совпадающие записи из левой и правой таблицы.
Заключение
диаграмме Венна лучше не использовать для обяснения операций Join
Джойны относительно легко понять интуитивно. И их сравнительно легко объяснить с помощью диаграмм Венна. Но всякий раз, когда Вы делаете это, запомните, что Вы делаете неправильную аналогию. JOIN не является строго заданной операцией над множествами, которая может быть описана диаграммами Венна. JOIN всегда декартово произведение с предикатом, и возможно UNION для добавления записей к результату OUTER JOIN.
Так что, если сомневаетесь, то применяйте диаграммы JOINов, лучше чем Диаграммы Венна. Они более точны и визуально более полезны.
Вопросы:
В заключение, эта статья об реляционные соединения подчеркивает важность того что вы тут, расширяете ваше сознание, знания, навыки и умения. Надеюсь, что теперь ты понял что такое реляционные соединения, операции над отношениями, реляционная алгебра и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Базы данных, знаний и хранилища данных. Big data, СУБД и SQL и noSQL
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Базы данных, знаний и хранилища данных. Big data, СУБД и SQL и noSQL
Термины: Базы данных, знаний и хранилища данных. Big data, СУБД и SQL и noSQL