Параметрические и зонные индексы

Привет, Вы узнаете о том , что такое параметрические индексы, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое параметрические индексы, зонные индексы , настоятельно рекомендую прочитать все из категории Базы данных, знаний и хранилища данных. Big data, СУБД и SQL и noSQL.

До сих пор мы рассматривали документ как последовательность терминов. На самом
деле большинство документов имеют дополнительную структуру. Электронные документы обычно сопровождаются метаданными (metadata), которые кодируются в виде,
распознаваемом компьютерами. Под метаданными мы понимаем конкретные виды данных о документе, например фамилию автора, название и дату публикации. Эти метаданные обычно содержат поля метаданных (fields), например дату создания и формат документа3
, а также фамилию автора и, возможно, название документа. Множество возможных значений этих полей следует считать конечным, например множество всех дат
создания документа ограничено.
Рассмотрим запрос “Найти документы, созданные Вильямом Шекспиром в 1601 году
и содержащие слова alas poor Yorick”. В этом случае обработка запроса сводится, как
обычно, к поиску пересечения инвертированных списков, за исключением того, что мы
можем объединить словопозиции как из стандартных инвертированных, так и из параметрических индексов (parametric indexes)4
. Для каждого поля (например, для даты создания) существует один параметрический индекс; он позволяет выбрать только те документы, которые соответствуют дате, указанной в запросе. На рис. 6.1 показан интерфейс
пользователя для параметрического поиска. Некоторые поля подразумевают упорядоченные значения (например, даты); в указанном выше запросе одним из таких значений
является год “1601”. Поисковая машина может поддерживать запросы с указанием диапазонов таких упорядоченных значений; для хранения набора значений поля можно использовать такие структуры данных, как B-деревья.
Зоны (zones) напоминают поля, но содержанием зоны может быть произвольный
текст. В то время как поле может иметь относительно небольшое множество значений,
зона может содержать произвольный и неограниченный объем текста. Например, названия документов и аннотации обычно трактуются как зоны. Для того чтобы поддержать

3 В отечественной и зарубежной практике очень часто вместо “поле метаданных” или “поле”
используется “атрибут” или “атрибут документа”. — Примеч. ред. 4 Также “атрибутивный индекс”, индекс “атрибутов документа” и “атрибутивный поиск”. — Примеч. ред.

обработку запросов вида “Найти документы со словами merchant в названии и William — в списке авторов, а также с фразой gentle rain в тексте” для каждой зоны документа можно создать стандартный инвертированный индекс. Такой индекс выглядит
примерно так, как показано на рис. 6.2. В то время как словарь для параметрического
индекса создается на основе фиксированного списка значений (множества языков, множества дат), словарь для зонного индекса формируется на основе текстов, размещенных
в данной зоне

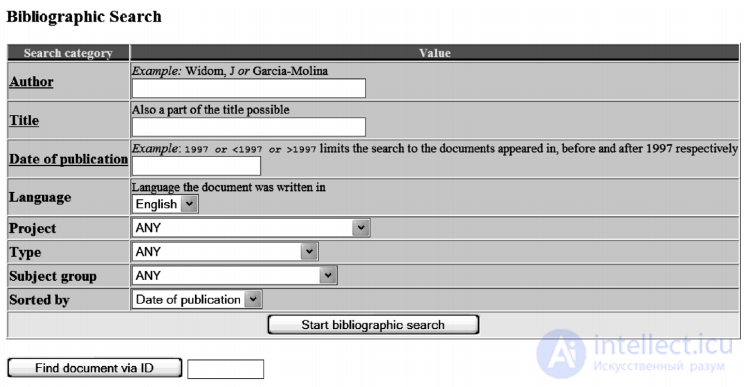
Рис. 6.1. Параметрический поиск. В данном примере мы имеем коллекцию с полями, позволяющими отбирать публикации по зонам, например Author (автор) или Language (язык)

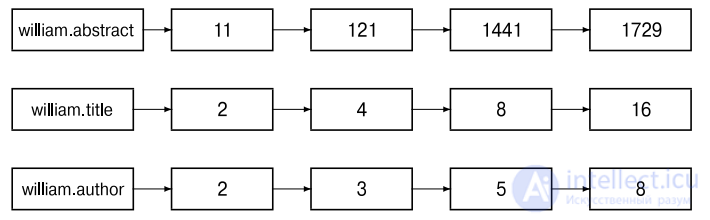
Рис. 6.2. Элементарный зонный индекс; зоны кодируются как расширения элементов словаря

На самом деле размер словаря можно уменьшить, закодировав зону, в которой встречается термин, в словопозиции. Например, на рис. 6.3 показано, как кодируется появление слова william в названии и в зоне авторов разных документов. Такое кодирование полезно, когда размер словаря имеет значение (поскольку мы требуем, чтобы словарь хранился в оперативной памяти). Однако существует еще одна причина, по которой кодирование, показанное на рис. 6.3, оказывается полезным: эффективное ранжирование взвешиванием по зонам (weighted zone scoring)

Рис. 6.3. Зонный индекс, в котором зона закодирована в словопозиции, а не в словаре

.1. Взвешенное зонное ранжирование

До сих пор в разделе 6.1 мы были сосредоточены на поиске документов на основе булевых запросов относительно полей и зон. Теперь перейдем ко второму приложению зон
и полей.
Обозначим булев запрос буквой q, а документ — буквой d. Метод взвешенного зонного ранжирования присваивает паре (q, d) значение релевантности из отрезка [0,1], вычисляя линейную комбинацию зонных показателей (zone score), в которую каждая зона
документа вносит булево значение. Об этом говорит сайт https://intellect.icu . Говоря конкретнее, рассмотрим множество документов, каждый из которых имеет l зон. Пусть 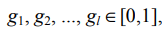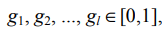, так что

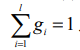
. Пусть si, где 1 ≤ i ≤ l, — булева величина, означающая соответствие (или его отсутствие) между
запросом q и i-й зоной. Например, если все термины запроса принадлежат конкретной
зоне, то ее булево значение должно быть равным единице, а если нет — нулю. Действительно, это отображение может осуществлять любая булева функция, отображающая наличие терминов запроса в зоне в множество {0, 1}. Таким образом, взвешенную зонную
релевантность можно определить как

Взвешенное зонное ранжирование иногда называется булевым поиском с ранжированием (ranked Boolean retrieval).

Пример 6.1. Рассмотрите запрос shakespeare к коллекции, в которой каждый документ имеет три зоны: author (автор), title (заголовок) и body (основной текст).
Булева функция ранжирования (Boolean score function) для зоны принимает значение, равное единице, если термин запроса shakespeare принадлежит этой зоне,
и нулю, если нет. Взвешенное зонное ранжирование в такой коллекции подразумевает использование трех весов, g1, g2 и g3, соответствующих зонам author,
title и body. Допустим, что g1 = 0,2, g2 = 0,3 и g3 = 0,5 (так что сумма всех трех весов равна единице); это соответствует приложению, в котором соответствие в
зоне author менее важно по сравнению со всеми другими зонами, соответствие
в зоне title является более важным, а соответствие в зоне body важнее всего.
Таким образом, если термин shakespeare появился в зонах title и body, но отсутствует в зоне author, то релевантность документа будет равна 0,8.
Как вычислить взвешенную зонную релевантность? Для этого можно просто поочередно вычислить релевантность для каждого документа, суммируя вклады разных зон.
Однако взвешенную зонную релевантность можно вычислить прямо по инвертированным индексам. Алгоритм, приведенный на рис. 6.4, предназначен для варианта, в котором запрос q содержит два термина, q1 и q2, и булеву функцию AND: 1 — если оба термина запроса присутствуют в зоне, и 0 — если нет. После алгоритма мы опишем его расширение для более сложных запросов и булевых функций

Читатели могли заметить большое сходство между алгоритмами, представленными на рис. 6.4 и 1.6. Действительно, они реализуют один и тот же проход по словопозициям, за исключением того, что вместо простого добавления документа в множество результатов для булева запроса AND в данном случае мы вычисляем релевантность каждого документа. В некоторых работах массив текущих значений релевантности scores[] называется множеством накопителей (accumulator). Это объясняется тем, что для более сложных по сравнению с операцией AND булевых функций релевантность документа может быть ненулевой, даже если он не содержит все термины запроса

Рис. 6.4. Алгоритм взвешенного зонного ранжирования по двум инвертированным спискам. Функция WeightedZone (здесь не показана) вычисляется во внутреннем цикле формулы (6.1)

2. Определение весов на основе машинного обучения

Как определить веса gi при взвешенном зонном ранжировании? Они могут быть указаны экспертами (или пользователем). Однако гораздо чаще веса определяются на основе обучающих примеров, оцененных заранее. Этот метод относится к общему классу методов ранжирования в информационном поиске под названием “методы ранжирования на основе машинного обучения” (machine-learned relevance). В данном разделе мы даем краткое введение в эту тему, поскольку взвешенное зонное ранжирование — хороший материал для такого изложения. Более полное описание требует понимания принципов машинного обучения,

1. В нашем распоряжении имеется множество обучающих примеров (training examples), каждый из которых представляет собой кортеж, состоящий из запроса q, документа d, а также оценки релевантности d и q. В простейшем случае каждая оценка релевантности (relevance judgment) является бинарной, т.е. релевантный или нерелевантный. В более сложных реализациях этой методологии используются более тонкие оценки.

2. Веса gi определяются путем “обучения” на данных примерах так, чтобы полученные
оценки аппроксимировали оценки релевантности обучающих примеров.

При взвешенном зонном ранжировании этот процесс можно рассматривать как подбор коэффициентов линейной функции от булевых признаков вхождения в соответствующие зоны. Затратной частью этой методологии является трудоемкий сбор оценок
релевантности, по которым производится обучение, особенно если коллекция часто изменяется (как веб). Опишем простой пример, показывающий, как свести задачу определения весов gi на основе обучения к простой задаче оптимизации.
Рассмотрим простой вариант взвешенного зонного ранжирования, в котором каждый
документ имеет зоны title и body. Применим к заданным запросу q и документу d булеву
функцию соответствия и вычислим булевы значения sT(d, q) и sB(d, q), указывающие, соответствует ли заголовок (соответственно, тело) документа d запросу q. Например, алгоритм, представленный на рис. 6.4, использует для этого функцию AND, примененную к
терминам запроса. Вычислим значение, лежащее между нулем и единицей, для каждой
пары (документ, запрос), используя значения s_T(d, q) и s_B(d, q) и константу g∈[0,1]:

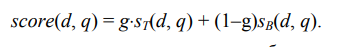(6.2)

Теперь опишем, как определить константу g по обучающим примерам, каждый из которых представляет собой тройку вида Φj = (dj, qj, r(di, qj)). Каждому обучающему примеру, содержащему документ di и запрос qi, человеком-редактором дается оценка релевантности r(di, qj), принимающая значение релевантный или нерелевантный. Этот процесс проиллюстрирован на рис. 6.5, на котором показаны семь примеров.

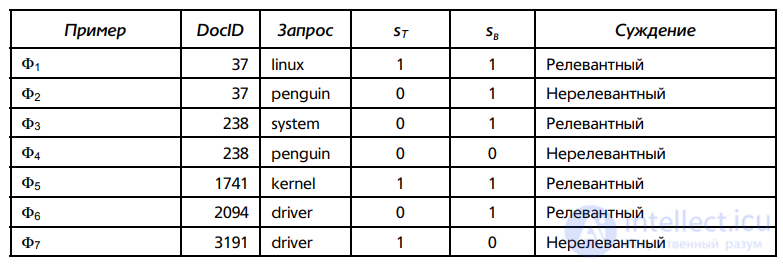
Рис. 6.5. Пример обучающих примеров Для каждого обучающего примера Φj у нас есть булевы значения s_T(dj, qj) и s_B(dj, qj), используемые для ранжирования по формуле (6.2).

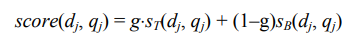(6.3)

Теперь сравним этот вычисленную релевантность с оценкой релевантности той же пары (dj, qj), сделанной человеком; для этого каждая оценка релевантный кодируется единицей, а нерелевантный — нулем. Допустим, что ошибка весовой функции с весом g определяется по следующей формуле

.

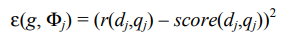
Здесь оценка редактора r(dj,qj) кодируется единицей или нулем. Таким образом, суммарная ошибка, соответствующая множеству обучающих примеров, равна

Теперь задача определения константы g по обучающим примерам сводится к нахождению значения g, минимизирующего суммарную ошибку (6.4). Определение наилучшего значения g на основе формулы (6.4) в формулировке раздела 6.1.3 сводится к задаче минимизации квадратичной функции, зависящей от g, на отрезке [0,1]. Эта тема обсуждается в разделе 3.

3. Оптимальный вес g

Отметим, что для любого обучающего примера Φj, такого, что sT(dj, qj) = 0 и sB(dj, qj) = 1, релевантность, вычисленная по формуле (6.2), равен 1–g. Аналогично можно записать релевантность, вычисленную по формуле (6.2) при трех других возможных комбинациях значений sT(dj, qj) и sB(dj, qj); эти комбинации продемонстрированы на рис. 6.6.

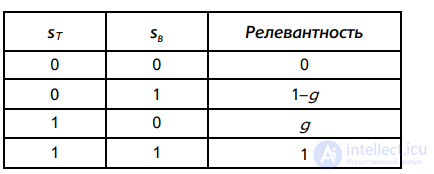
Рис. 6.6. Четыре возможные комбинации sT и sB

Обозначим через n_01r (соответственно, n_01n) количество обучающих примеров, для которых sT(dj, qj) = 0 и sB(dj, qj) = 1, а экспертная оценка — релевантный (соответственно, нерелевантный). Тогда вклад в суммарную ошибку в выражении (6.4) от обучающих примеров, для которых sT(dj, qj) = 0 и sB(dj, qj) = 1, равен

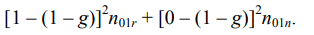
Записав аналогичным образом вклады в ошибку от обучающих примеров при трех других комбинациях значений sT(dj, qj) и sB(dj, qj) (и расширив обозначения очевидным образом), приходим к выводу, что суммарная ошибка, определяемая по формуле (6.4), равн

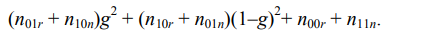. (6.5)

Дифференцируя выражение (6.5) по g и приравнивая результат к нулю, получаем, что оптимальное значение g равно

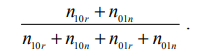. (6.6)

Задания для самопроверки

Упражнение 6.1. Необходимо ли, чтобы при использовании метода взвешенного
зонного ранжирования все зоны использовали одну и ту же булеву функцию совпадения (соответствия)?

Упражнение 6.2. Примем в примере 6.1 следующие веса: g1 = 0,2, g2 = 0,31 и g3 = 0,49. Перечислите все отличающиеся друг от друга значения, которые может иметь документ.

Упражнение 6.3. Перепишите алгоритм, представленный на рис. 6.4, для случая, когда запрос содержит больше двух терминов.

Упражнение 6.4. Напишите псевдокод для функции WeightedZone для случая двух инвертированных списков, как на рис. 6.4.

Упражнение 6.5. Примените формулу (6.6) к набору обучающих примеров, представленному на рис. 6.5, и оцените наилучшее значение g.

Упражнение 6.6. Для значения g, найденного в упражнении 6.5, вычислите релевантность документа с помощью метода взвешенного зонного ранжирования для
каждого примера (запрос, документ). Как эта релевантность соотносится с экспертными оценками, указанными на рис. 6.5 (суждения закодированы числами 0 и 1)?

Упражнение 6.7. Почему выражение для величины g в формуле (6.6) не учитывает обучающие примеры, для которых значения sT(dj, qj) и sB(dj, qj) одинаковы?

Вау!! 😲 Ты еще не читал? Это зря!

• Частота термина и взвешивание
• ранжирование документа
• Варианты функций tf–idf
• Сжатие инвертированного файла
• инвертированный индекс , inverted index , сжатие инвертированного файла ,
• Сжатие словаря
• Статистические характеристики терминов в информационном поиск

Исследование, описанное в статье про параметрические индексы, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое параметрические индексы, зонные индексы и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Базы данных, знаний и хранилища данных. Big data, СУБД и SQL и noSQL