Лекция
Привет, Вы узнаете о том , что такое инвертированный индекс, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое инвертированный индекс, inverted index , сжатие инвертированного файла , настоятельно рекомендую прочитать все из категории Обработка естественного языка.
инвертированный индекс (англ. inverted index) — структура данных, в которой для каждого слова коллекции документов в соответствующем списке перечислены все документы в коллекции, в которых оно встретилось. Инвертированный индекс используется для поиска по текстам.
Есть два варианта инвертированного индекса:
Последняя форма предлагает больше функциональных возможностей (например, поиск фраз ), но требует больше вычислительной мощности и места для создания.

Рис 1 пример прямого и обратного(инвертированного ) индекса
такое храненние данных похволяет быство выполнять поиск лбого документа , однако результаты поиска необходимо ранжировать по определенным алгоритмам например с использованием метрики tf-idf .
Опишем, как решается задача нахождения документов, в которых встречаются все слова из поискового запроса. При обработке однословного поискового запроса ответ уже есть в инвертированном индексе — достаточно взять список, соответствующий слову из запроса. При обработке многословного запроса берутся списки, соответствующие каждому из слов запроса и пересекающиеся.
Обычно в поисковых системах после построения с помощью инвертированного индекса списка документов, содержащих слова из запроса, идет ранжирование документов из списка. Инвертированный индекс — это самая популярная структура данных, которая используется в информационном поиске.
Инвертированный индекс можно хранить в так называемой инверсной таблице
Пусть у нас есть корпус из трех текстов "it is what it is",
"what is it" и
"it is a banana", тогда инвертированный индекс будет выглядеть следующим образом:
"a": {2}
"banana": {2}
"is": {0, 1, 2}
"it": {0, 1, 2}
"what": {0, 1}
Здесь цифры обозначают номера текстов, в которых встретилось соответствующее слово. Тогда отработка поискового "what is it" запроса даст следующий результат .
У вас есть тысячи-сотни тысяч страниц на веб-сайте, которые нажно обработать и сохранить в трех таблицах в виде инвертированного индекса.
таблица document
- Docid (ПК, FK)
- URL
- charactercount
- WordCount
Charactercount и wordcount помогают мне определить длинный документ из краткого, который я могу использовать позже.
таблица word
- Wordid (PK, FK)
- слово
- doc_freq
- inverse_doc_freq
Для вычисления inverse_doc_freq я использую вымышленное большое число (100000000), чтобы предотвратить общий пересчет документов.
LOC
- wordid
- DocId
- word_freq
- вес
(Wordid & docid объединены уникально)
Вес - это оценка, рассчитанная на простой основе, например слово в заголовке + слово в url + слово frquency и т. Д.
Для поиска нужно выполнить следущее
Запрос необходимо агрегировать на уровне таблицы document
.
SELECT d.docid, d.url, sum(weight) AS weight
FROM document d
JOIN loc l on d.docid = l.docid
JOIN word w on w.wordid = l.wordid
WHERE w.word in ('intellect.icu', 'intellect', 'icu')
GROUP by d.docid
ORDER by weight DESC;
В списке вхождений слова в документы помимо id документов обычно также указываются факторы (TF-IDF, бинарный фактор: «попало слово в заголовок или не попало», другие факторы), которые используются при ранжировании. Индекс может строиться не по всем словоформам, а по леммам (по каноническим формам слов). Стоп-слова можно исключить и не строить для них индекс, считая что каждое из них встречается почти во всех документах корпуса. Для ускорения вычисления пересечений используют эвристику skip-pointer-ов. При обработке запросов, содержащих много слов, используют функцию кворума, которая пропускает на следующую стадию ранжирования часть документов, в которых встретились не все слова из запроса.
По историческим причинам сжатие инвертированных списков и сжатие растровых изображений были разработаны как отдельные направления исследований и только позже были признаны решающими, по сути, ту же проблему.
Преимущества сжатия очевидны: требуется меньше дисковой памяти и, как будет показано далее, легко можно достичь коэффициента сжатия 1:4 и тем самым снизить стоимость хранения индекса на 75%.
Однако у сжатия есть два менее заметных преимущества. Во-первых, оно повышает
эффективность использования кэша. Поисковые системы применяют некоторые части
словарей и индекса чаще остальных. Например, если поместить в кэш инвертированный
список часто используемого термина запроса t, то все вычисления, необходимые для поиска ответа на запрос, состоящий из одного термина t, можно выполнить в оперативной
памяти. Применив сжатие, мы можем поместить в оперативную память больше информации. При обработке запросов, содержащих термин t, вместо выполнения затратных
операций по перемещению головки диска можно обращаться к инвертированному списку, хранящемуся в оперативной памяти, и распаковывать его. Как будет показано ниже,
существуют простые и эффективные методы распаковки данных, поэтому накладные
расходы на распаковку инвертированного списка невелики. В результате мы можем существенно уменьшить время ответа информационно-поисковой системы. Поскольку
оперативная память дороже, чем память на диске, основным стимулом для использования сжатия часто является ускорение работы за счет кэширования, а не за счет уменьшения требований к объему дискового пространства.
Во-вторых, еще менее заметное преимущество сжатия — более быстрая загрузка
данных с диска в оперативную память. На современном аппаратном обеспечении эффективные алгоритмы распаковки работают настолько быстро, что общее время, затрачиваемое на передачу сжатой порции данных с диска, а затем на распаковку, обычно
меньше, чем время, необходимое для передачи той же самой порции данных в несжатом
виде. Например, загрузив инвертированный список намного меньшего размера, можно
сократить время на выполнение операций ввода-вывода, даже с учетом дополнительного
времени, требуемого для распаковки. Итак, в большинстве случаев системы информационного поиска, использующие сжатые инвертированные списки, работают быстрее, чем
системы, в которых эти списки хранятся в развернутом виде.
Если основной целью сжатия является экономия дисковой памяти, то скорость сжатия не играет большой роли. Однако для более рационального использования кэша и более быстрой загрузки данных с диска в оперативную память скорость распаковки должна
быть высокой. Алгоритмы сжатия, обсуждаемые в этой главе, весьма эффективны, а значит, позволяют использовать все преимущества сжатия индекса.
В данной главе словопозиция (posting) в инвертированном списке интерпретируется
как идентификатор документа docID. Например, инвертированный список (6; 20, 45, 100 где 6 — идентификатор термина из списка, содержит три координаты. Об этом говорит сайт https://intellect.icu . Как указывалось
в разделе 2.4.2, словопозиции в большинстве поисковых систем, как правило, содержат
информацию о частоте и координатах термина
Таблица 4.2. Характеристики коллекции Reuters–RTV1. Значения округлены для удобства вычислений, которые приводятся в данной книге. Неокругленные значения таковы: 806 791 документ, 222 лексемы на документ, 391 523 (разных) термина, 6,04 байт на лексему с пробелами и знаками пунктуации, 4,5 байт на лексему без пробелов и знаков пунктуации, 7,5 байт на термин и 96 969 056 лексем. Числа в этой таблице соответствуют третьей строке табл. 5.1 (“без учета регистра”).

Напомним (см. табл. 4.2), что коллекция Reuters–RCV1 содержит 800 тысяч документов, 200 лексем в документе, шесть символов в лексеме и 100 миллионов словопозиций,
причем для простоты в рамках этой главы мы считаем, что эта словопозиция состоит
только из идентификатора документа docID, т.е. не содержит информации о частоте и
координатах слова в документе. Эти числа соответствуют строке 3 (“свертывание регистра”) в табл. 5.1.
Идентификаторы документов занимают log2 800 000 ≈ 20 бит. Следовательно, размер коллекции равен примерно 800 000 × 200 × 6 байт = 960 Мбайт, а размер несжатого инвертированного файла равен 100 000 000 × 20/8 = 250 Мбайт.
Для более рационального представления инвертированных файлов, использующих
менее 20 бит на документ, отметим, что словопозиции частых терминов имеют близкие
значения.
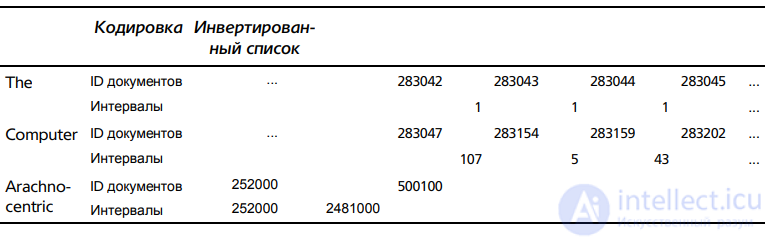
Мысленно пройдем по документам коллекции и поищем часто встречающийся
термин computer. Мы найдем документ, содержащий слово computer, затем пропустим несколько документов, не содержащих это слово, после найдем документ, содержащий этот термин, и т.д. (табл. 5.3). Ключевая идея заключается в том, что интервалы
между словопозициями являются короткими и для их хранения требуется меньше 20 бит.
На практике интервалы между наиболее частыми терминами, таким как the и for, чаще
всего равны единице. Однако пробелы между редкими терминами, встречающимися в
коллекции лишь один или два раза (например, слово arachnocentric в табл. 5.3), по
величине мало отличаются от идентификаторов документов и требуют для хранения
20 бит.
Для экономного представления такого распределения интервалов необходим метод упаковки с использованием кодов переменной длины (variable encoding method), который для более коротких интервалов использует меньше битов.
Таблица 5.3. Кодирование интервалов вместо идентификаторов документов. Например,
мы храним интервалы 107, 5, 43, ... вместо идентификаторов документов 283154, 283159,
283202, ... для термина computer. Первый идентификатор документа остается неизменным
(показан только для термина arachnocentric)
Для того чтобы закодировать небольшие числа, используя меньше памяти, чем для
кодирования больших чисел, рассмотрим два вида методов: байтовое сжатие (bytewise
compression) и битовое сжатие (bitwise compression). Как следует из их названий, эти методы кодируют интервалы в минимальное количество байтов и битов соответственно.
Байтовое кодирование переменной длины (variable byte encoding — VB, или variable
byte coding — VBC) использует для кодирования интервалов целое количество байтов.
Последние 7 бит в каждом байте являются “полезной нагрузкой” и кодируют часть интервала. Первый бит байта является битом продолжения (continuation bit). Он равен
единице у последнего байта закодированного интервала и нулю в остальных случая

Рис. 5.8. Кодирование и декодирование по схеме VB. Функции div и mod вычисляют целочисленное частное и остаток после целочисленного деления соответственно. Функция Prepend добавляет элемент в начало списка, например Prepend(〈1, 2〉, 3) = (3, 1, 2). Функция Extend расширяет список, например Extend(〈1, 2〉, 〈3, 4〉) = (1, 2, 3, 4)
Для декодирования кода, закодированного переменным количеством байтов, считывается последовательность байтов, бит продолжения которых равен нулю, завершающаяся байтом, в котором бит продолжения равен единице. Затем извлекаются и конкатенируются семибитовые части. Псевдокод байтового кодирования и декодирования переменной длины приведен на рис. 5.8, а пример инвертированного списка, закодированного по схеме VB, — в табл. 5.
Обратите внимание на то, что в таблице начальное значение равно нулю. Поскольку кодировать идентификатор документа или нулевой интервал бессмысленно, на практике начальное значение обычно равно единице, так что 10000000 — это код единицы, 10000101 — шестерки (а не пятерки, как в таблице), и т.д
Таблица 5.4. Байтовое кодирование переменной длины. Интервалы закодированы с помощью целого числа байтов. Первый бит представляет собой бит продолжения и означает, заканчивается код этим байтом (1) или нет (0).

Как показал эксперимент, при использовании байтового кодирования переменной длины размер сжатого индекса для коллекции Reuters–RCV1 равен 116 Мбайт. Это означает, что экономия памяти по сравнению с несжатым индексом превышает 50% (табл. 5.6).
Идею байтового кодирования переменной длины можно применить к единицам памяти, которые могут быть как больше, так и меньше байта: 32-, 16- и 4-битовые слова, или полубайты (nibbles). Более крупные слова еще сильнее уменьшают объем необходимых манипуляций битами за счет потери качества сжатия. Размеры слов, не превышающие байта, позволяют достичь еще более высоких степеней сжатия за счет увеличения количества манипуляций битами. В целом байты представляют собой приемлемый компромисс между степенью сжатия и скоростью распаковки.
Для большинства систем информационного поиска байтовое кодирование переменной длины обеспечивает превосходный компромисс между скоростью поиска и размером памяти. Кроме того, его легко реализовать — большинство альтернатив, упомянутых в разделе 5.4, являются более сложными. Однако, если дисковая память ограничена, можно достичь более высокой степени сжатия, применив побитовое кодирование, в частности две тесно связанные одна с другой схемы: γ-коды, которые будут рассмотрены ниже, и δ-коды (упражнение 5.9)
В схеме VB переменное количество байтов зависит от размера интервала. Методы битового уровня адаптируют длину кода на уровне битов. Простейшим битовым кодом является унарный код (unary code). Унарный код числа n представляет собой строку, состоящую из n единиц, за которыми следует нуль (см. первые два столбца в табл. 5.5). Очевидно, что это не очень эффективный код, но в свое время он нам пригодится.
Таблица 5.5. Примеры унарных и γ-кодов. Унарные коды показаны только для небольших чисел. Запятые в γ-кодах вставлены только для читабельности и не являются частью реальных кодов

Насколько эффективным может быть код в принципе? Предположим, что 2n интервалов G, где 1 ≤ G ≤ 2n
, являются равновероятными. Тогда оптимальное кодирование для
каждого интервала G должно использовать n битов. В таком случае некоторые интервалы (в данном случае — G = 2n
) невозможно закодировать с помощью менее чем log2 G
бит. Наша цель — максимально приблизиться к нижней границе.
Метод, близкий к оптимальному, называется γ-кодированием (γ-encoding). Эта схема
использует кодирование с переменной длиной с помощью разбиения интервала G на пару, состоящую из длины (length) и смещения (offset). Смещение представляет собой запись числа G в двоичном виде с удаленной ведущей единицей. 5 Например, для числа 13
(бинарный код — 1101) смещение равно 101. Параметр длина кодирует длину смещения
в унарном коде. Для числа 13 длина смещения равна 3 бит. В унарном коде это число выглядит как 1110. Следовательно, γ-код числа 13 имеет вид 1110101. Он представляет собой конкатенацию длины 1110 и смещения 101. Другие примеры γ-кода приведены в
правом столбце табл. 5.5.
Для того чтобы декодировать γ-код, сначала необходимо прочитать унарный код, пока не будет обнаружен нуль, который его завершает, например четыре бита 1110 при
расшифровке числа 1110101. Теперь нам известна длина смещения: 3 бит. После этого
можно правильно считать смещение 101 и добавить единицу, удаленную при кодировании: 101 → 1101 = 13.
Длина смещения (offset) равна ⎣log2 G⎦ бит, а длина параметра длина (length) равна
⎣log2 G⎦ + 1 бит. Таким образом, длина всего кода равна 2 × ⎣log2 G⎦ + 1 бит. Все γ-коды
имеют нечетную длину и всего в два раза больше длины оптимального кода, которая
равна ⎣log2 G⎦. Это оптимальное значение определено на основе предположения, что все
2n интервалов от 1 до 2n являются равновероятными. Однако на практике это условие
может не выполняться. Как правило, априори распределение вероятностей интервалов
неизвестно.
Свойства дискретного распределения вероятностей 6 P (включая то, является ли код оптимальным) характеризуются энтропией H(P), которая определяется следующим образом.
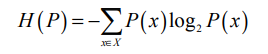
Здесь X — множество всех возможных чисел, которые необходимо закодировать (и следовательно,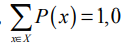 ).
).
Энтропия (entropy) — это мера неопределенности, что иллюстрирует рис. 5.9 для распределения вероятностей P среди двух исходов X = [x1, x2]. Энтропия достигает максимального уровня (H(P) = 1) при P(x1) = P(x2) = 0,5, когда неопределенность относительно того, какой из исходов xi будет следующим, является наибольшей. Минимальный уровень энтропии (H(P) = 0) достигается при P(x1) = 0 и P(x2) = 1, когда существует полная определенность.
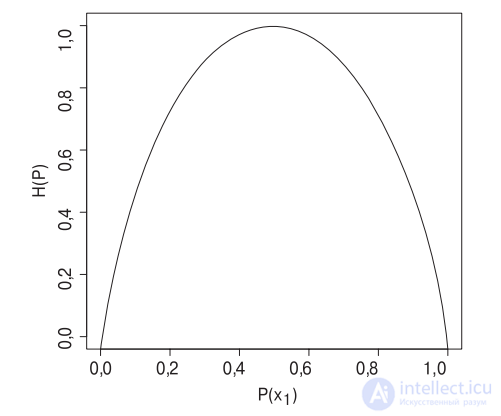
Рис. 5.9. Энтропия H(P) как функция, зависящая от P(x1) на пространстве, состоящем из двух исходов, x1 и x2
Можно показать (см. библиографию), что при определенных условиях нижняя граница E(L) ожидаемой длины кода L равна H(P). Кроме того, можно доказать, что при условии 1 < H(P) < ∞ γ-кодирование не больше чем в три раза отличается от оптимального, а
при больших значениях H(P) этот показатель приближается к двум.
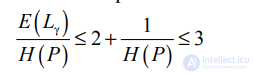
Примечательно, что это соотношение сохраняется при любых распределениях вероятностей P. Итак, даже не зная никаких свойств распределения интервалов, мы можем применять γ-кодирование и быть уверенными, что при большой энтропии полученный
код лишь примерно в два раза больше оптимального. Код, длина которого при произвольном распределении вероятностей P отличается от оптимальной лишь на множитель,
называется универсальным (universal).
Кроме универсальности, γ-коды обладают еще двумя свойствами, полезными при
сжатии индекса. Первое свойство — γ-код является беспрефиксным (prefix free), т.е. ни
один γ-код не является префиксом другого кода. Это значит, что декодирование последовательности γ-кодов всегда является однозначным, и нам не нужны разделители между
ними, которые снижают эффективность кодов. Второе свойство заключается в том, что
γ-коды являются непараметрическими (parameter free). При использовании многих других эффективных кодов необходимо уточнять параметры распределения интервалов в
индексе (например, параметры биномиального распределения). Это усложняет реализацию сжатия и распаковки. Например, параметры необходимо хранить в памяти и извлекать из нее. Кроме того, при динамическом индексировании распределение интервалов
может изменяться, поэтому исходные параметры больше использовать нельзя. Непараметрический код позволяет избежать этих проблем.
Какой степени сжатия инвертированного индекса достигают γ-коды? Для ответа на
этот вопрос применим закон Ципфа — модель распределения терминов, введенную в
разделе 5.1.2. В соответствии с законом Ципфа частота термина в коллекции cfi обратно
пропорциональна рангу, т.е. существует константа c', такая, что

Можно выбрать другую константу c, такую, что дроби c/i представляют собой относительные частоты, а их сумма равна единице (т.е. c/i = cfi/T).

Здесь M — количество различных терминов, а HM — M-е гармоническое число.
В коллекции Reuters–RCV1 содержится M = 400 тысяч разных терминов, а HM ≈ lnM. Таким образом,
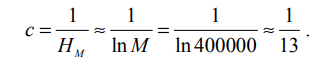
Следовательно, относительная частота i-го термина примерно равна 1/(13i), а ожидаемое среднее количество терминов в документе длины L равно
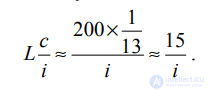
Здесь вероятность появления термина заменена его относительной частотой. Напомним, что 200 — это среднее количество лексем в документе из коллекции Reuters–RCV1
(табл. 4.2).
Итак, мы определили статистические показатели термина, характеризующие распределение термина в коллекции и распределение интервалов в инвертированном списке. На основе этих показателей можно вычислить требования к памяти, необходимой для хранения инвертированного индекса, сжатого с помощью γ-кодирования. Сначала разобьем отсортированный по убыванию частоты лексикон терминов коллекции на блоки, размеры которых равны Lc = 15. В среднем i-й термин в документе встречается 15/i раз. Следовательно, среднее количество появлений в документе f для терминов из первого блока удовлетворяет условию f ≥1 , что соответствует общему количеству интервалов в расчете на один термин (gaps per term), равному N. Среднее количество появлений терминов из второго блока в документе удовлетворяет условию
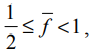
, что соответствует общему количеству интервалов в расчете на один термин, равному N/2. Среднее количество появлений терминов из третьего блока в документе удовлетворяет условию
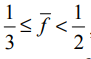
, что соответствует общему количеству интервалов в расчете на один термин, равному N/3 и т.д. (Мы выбираем нижнюю границу, поскольку это упростит дальнейшие вычисления. Как будет показано, даже при таком предположении окончательный результат слишком пессимистичен.) Примем довольно нереалистичное предположение, что все интервалы для заданного термина имеют одинаковые размеры, как показано на рис. 5.10.
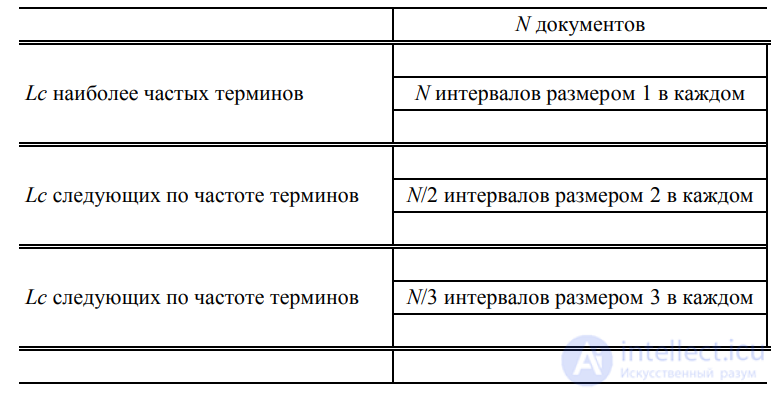
Рис. 5.10. Стратификация терминов для оценки размера инвертированного индекса, закодированного с помощью γ-кода
Сделав предположение, что интервалы распределены равномерно, мы в первом блоке
получим интервалы размером 1, во втором блоке — интервалы размером 2, и т.д.
Кодируя N/j интервалов размером j с помощью γ-кодов, можно определить количество битов, необходимых для хранения инвертированного списка термина в j-м блоке
(соответствует одной строке на рис. 5.10).
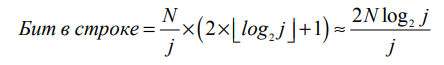
Для кодировки всего блока необходимо Lc ⋅ 2Nlog2j/j бит. Общее количество блоков
равно M/(Lc), поэтому инвертированный файл в целом займет

Для коллекции Reuters–RCV1 ( M/ Lc ) ≈ 400 000/15 ≈ 27 000 и
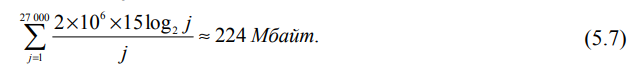
Итак, инвертированный файл сжатого инвертированного индекса для коллекции объемом 960 Мбайт занимает 224 Мбайт, т.е. одну четвертую исходной коллекции. Запустив γ-сжатие коллекции Reuters–RСV1, мы сжали индекс еще больше — до 101 Мбайт, что составляет чуть больше одной десятой размера коллекции. Причины такого расхождения между предсказанным и реальным значениями заключается в том, что (1) закон Ципфа не очень хорошо аппроксимирует фактическое распределение частот терминов в коллекции Reuters–RCV1 и (2) интервалы распределены неравномерно. В соответствии с моделью Ципфа для неокругленных данных из табл. 4.2 размер индекса должен быть равен 251 Мбайт. Если сгенерировать частоты терминов по модели Ципфа и для этих искусственных терминов создать сжатый индекс, то его размер будет равен 254 Мбайт. Следовательно, предсказания модели остаются верными в той мере, в какой выполняются предположения относительно распределения частот терминов. Результаты применения методов сжатия, описанных в главе, приведены в табл. 5.6. Размер матрицы инцидентности терминов (рис. 1.1) для коллекции Reuters–RCV1 равен 400 000 × 800 000 = 40 × 8 × 109 бит, или 40 Гбайт
Таблица 5.6. Сжатие индекса и лексикона для коллекции Reuters–RCV1. Коэффициент сжатия зависит от доли собственно текста в коллекции. Коллекция Reuters–RCV1 содержит большое количество разметки XML. Поэтому, используя две лучшие схемы сжатия — γ-кодирование и блочное хранение с фронтальной упаковкой, — можно получить очень маленькие значения коэффициента сжатия индекса относительно размера исходной коллекции для Reuters–RCV1: (101 + 5,9)/3600 ≈ 0,03

Схема γ-кодирования коллекции Reuters–RCV1 позволяет достичь отличного сжатия — почти на 15% лучшего, чем схема байтового кодирования переменной длины. Однако ее декодирование является затратным. Это объясняется большим количество побитовых операций — сдвигов и применения масок, — которые необходимы для дешифровки последовательности γ-кодов, поскольку границы между кодами обычно расположены где-то в середине машинного слова
. В результате процесс обработки запроса при использовании γ-кодирования становится более затратным, чем при использовании схемы байтового кодирования переменной длины. Выбор между этими двумя схемами зависит от особенностей приложения, например от относительной важности экономии дисковой памяти по сравнению со скоростью обработки запросов. Коэффициент сжатия индекса в табл. 5.6 приблизительно равен 25%:
400 Мбайт (несжатый, каждая словопозиция хранится в виде 32-битового слова) по сравнению с 101 Мбайт (γ-кодирование) и 116 Мбайт (байтовое кодирование переменной длины). Это значит, что как схема γ-кодирования, так и схема байтового кодирования переменной длины достигают цели, поставленной в начале главы. Сжатие индекса существенно повышает скорость поиска и эффективность использования памяти за счет уменьшения требуемой дисковой памяти, одновременно увеличивая объем информации, которую необходимо хранить в кэше, и ускоряя передачу данных с диска в оперативную память.
Прочтение данной статьи про инвертированный индекс позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое инвертированный индекс, inverted index , сжатие инвертированного файла и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Обработка естественного языка
Комментарии
Оставить комментарий
Обработка естественного языка
Термины: Обработка естественного языка