3.8.2. Сортировки включением - 3. СТАТИЧЕСКИЕ СТРУКТУРЫ ДАННЫХ

Это продолжение увлекательной статьи про статические структуры данных.

...

интервалом d} while k do { цикл, пока есть перестановки } begin k:=false; i:=1; for i:=1 to N-d do { сравнение эл-тов на интервале d } begin if a[i] > a[i+d] then begin t:=a[i]; a[i]:=a[i+d]; a[i+d]:=t; { перестановка } k:=true; { признак перестановки } end; { if ... } end; { for ... } end; { while k } d:=d div 2; { уменьшение интервала } end; { while d>0 } end;

Результаты трассировки программного примера 3.10 представлены в таблице 3.7.

Шаг	d	Содержимое массива а
Исходный		76 22_ 4 17 13 49_ 4 18 32 40 96 57 77 20_ 1 52
1	8	32 22_ 4 17 13 20_ 1 18 76 40 96 57 77 49_ 4 52
2	8	32 22_ 4 17 13 20_ 1 18 76 40 96 57 77 49_ 4 52
3	4	13 20_ 1 17 32 22_ 4 18 76 40_ 4 52 77 49 96 57
4	4	13 20_ 1 17 32 22_ 4 18 76 40_ 4 52 77 49 96 57
5	2	13 20_ 1 17 32 22_ 4 18 76 40_ 4 52 77 49 96 57
6	2	13 20_ 1 17 32 22_ 4 18 76 40_ 4 52 77 49 96 57
7	2	_1 17_ 4 18_ 4 20 13 22 32 40 76 49 77 52 96 57
8	2	_1 17_ 4 18_ 4 20 13 22 32 40 76 49 77 52 96 57
9	1	_1_ 4 17_ 4 18 13 20 22 32 40 49 76 52 77 57 96
10	1	_1_ 4_ 4 17 13 18 20 22 32 40 49 52 76 57 77 96
11	1	_1_ 4_ 4 13 17 18 20 22 32 40 49 52 57 76 77 96
12	1	_1_ 4_ 4 13 17 18 20 22 32 40 49 52 57 76 77 96
Результат		_1_ 4_ 4 13 17 18 20 22 32 40 49 52 57 76 77 96

Таблица 3.7

3.8.2. Сортировки включением

Сортировка простыми вставками.

Этот метод - "дословная" реализации стратегии включения. Порядок алгоритма сортировки простыми вставками - O(N^2), если учитывать только операции сравнения. Но сортировка требует еще и в среднем N^2/4 перемещений, что де- лает ее в таком варианте значительно менее эффективной, чем сортировка выборкой.

Алгоритм сортировки простыми вставками иллюстрируется программным примером 3.11.

 {===== Программный пример 3.11 =====}
 Procedure Sort(a : Seq; var b : Seq);
   Var i, j, k : integer;
   begin
     for i:=1 to N do begin  { перебор входного массива }
       { поиск места для a[i] в выходном массиве }
       j:=1; while (j < i) and (b[j] <= a[i]) do j:=j+1;
       { освобождение места для нового эл-та }
       for k:=i downto j+1 do b[k]:=b[k-1];
       b[j]:=a[i];        { запись в выходной массив }
       end; end;

Эффективность алгоритма может быть несколько улучшена при применении не линейного, а дихотомического поиска. Однако, следует иметь в виду, что такое увеличение эффективности может быть достигнуто лишь на множествах значительного по количеству элементов объема. Т.к. алгоритм требует большого числа пересылок, при значительном объеме одной записи эффективность может определяться не количеством операций сравнения, а количеством пересылок.

Реализация алгоритма обменной сортировки простыми вставками отличается от базового алгоритма только тем, что входное и выходное множество разделяют одну область памяти.

Пузырьковая сортировка вставками.

Это модификация обменного варианта сортировки. В этом методе входное и выходное множества находятся в одной последовательности, причем выходное - в начальной ее части. В исходном состоянии можно считать, что первый элемент последовательности уже принадлежит упорядоченному выходному множеству, остальная часть последовательности - неупорядоченное входное. Первый элемент входного множества примыкает к концу выходного множества. На каждом шаге сортировки происходит перераспределение последовательности: выходное множество увеличивается на один элемент, а входное - уменьшается. Это происходит за счет того, что первый элемент входного множества теперь считается последним элементом выходного. Затем выполняется просмотр выходного множества от конца к началу с перестановкой соседних элементов, которые не соответствуют критерию упорядоченности. Просмотр прекращается, когда прекращаются перестановки. Это приводит к тому, что последний элемент выходного множества "выплывает" на свое место в множестве. Поскольку при этом перестановка приводит к сдвигу нового в выходном множестве элемента на одну позицию влево, нет смысла всякий раз производить полный обмен между соседними элементами - достаточно сдвигать старый элемент вправо, а новый элемент записать в выходное множество, когда его место будет установлено. Именно так и построен программный пример пузырьковой сортировки вставками - 3.12.

 {===== Программный пример 3.12 =====}
 Procedure Sort (var a : Seq);
 Var i, j, k, t : integer;
 begin
   for i:=2 to N do begin  { перебор входного массива }
   {*** вх.множество - [i..N], вых.множество - [1..i] }
     t:=a[i]; { запоминается значение нового эл-та }
     j:=i-1; {поиск места для эл-та в вых. множестве со сдвигом}
       { цикл закончится при достижении начала или, когда
         будет встречен эл-т, меньший нового }
       while (j >= 1) and (a[j] > t) do begin
         a[j+1]:=a[j]; { все эл-ты, большие нового сдвигаются }
         j:=j-1; { цикл от конца к началу выходного множества }
         end;
       a[j+1]:=t; { новый эл-т ставится на свое место }
       end;
 end; 

Результаты трассировки программного примера 3.11 представлены в таблице 3.8.

Шаг	Содержимое массива a
Исходный	48:43 90 39_ 9 56 40 41 75 72
1	43 48:90 39_ 9 56 40 41 75 72
2	43 48 90:39_ 9 56 40 41 75 72
3	39 43 48 90:_9 56 40 41 75 72
4	_9 39 43 48 90:56 40 41 75 72
5	_9 39 43 48 56 90:40 41 75 72
6	_9 39 40 43 48 56 90:41 75 72
7	_9 39 40 41 43 48 56 90:75 72
8	_9 39 40 41 43 48 56 75 90:72
Результат	_9 39 40 41 43 48 56 72 75 90:

Таблица 3.8

Хотя обменные алгоритмы стратегии включения и позволяют сократить число сравнений при наличии некоторой исходной упорядоченности входного множества, значительное число пересылок существенно снижает эффективность этих алгоритмов. Поэтому алгоритмы включения целесообразно применять к связным структурам данных, когда операция перестановки элементов структуры требует не пересылки данных в памяти, а выполняется способом коррекции указателей (см. главу 5).

Еще одна группа включающих алгоритмов сортировки использует структуру дерева. Мы рекомендуем читателю повторно вернуться к рассмотрению этих алгоритмов после ознакомления с главой 6.

Сортировка упорядоченным двоичным деревом.

Алгоритм складывается из построения упорядоченного двоичного дерева и последующего его обхода. Если нет необходимости в построении всего линейного упорядоченного списка значений, то нет необходимости и в обходе дерева, в этом случае применяется поиск в упорядоченном двоичном дереве. Алгоритмы работы с упорядоченными двоичными деревьями подробно рассмотрены в главе 6. Отметим, что порядок алгоритма - O(N*log2(N)), но в конкретных случаях все зависит от упорядоченности исходной последовательности, который влияет на степень сбалансированности дерева и в конечном счете - на эффективность поиска.

Турнирная сортировка.

Этот метод сортировки получил свое название из-за сходства с кубковой системой проведения спортивных соревнований: участники соревнований разбиваются на пары, в которых разыгрывается первый тур; из победителей первого тура составляются пары для розыгрыша второго тура и т.д. Алгоритм сортировки состоит из двух этапов. На первом этапе строится дерево: аналогичное схеме розыгрыша кубка.

Например, для последовательности чисел a:

               16 21 8 14 26 94 30 1

такое дерево будет иметь вид пирамиды, показанной на рис.3.13.

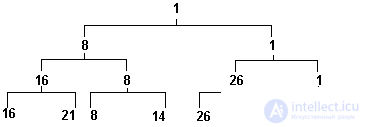
Рис.3.13. Пирамида турнирной сортировки

В примере 3.12 приведена программная иллюстрация алгоритма турнирной сортировки. Она нуждается в некоторых пояснениях. Построение пирамиды выполняется функцией Create_Heap. Пирамида строится от основания к вершине. Элементы, составляющие каждый уровень, связываются в линейный список, поэтому каждый узел дерева помимо обычных указателей на потомков - left и right - содержит и указатель на "брата" - next. При работе с каждым уровнем указатель содержит начальный адрес списка элементов в данном уровне. В первой фазе строится линейный список для нижнего уровня пирамиды, в элементы которого заносятся ключи из исходной последовательности. Следующий цикл while в каждой своей итерации надстраивает следующий уровень пирамиды. Условием завершения этого цикла является получение списка, состоящего из единственного элемента, то есть, вершины пирамиды. Построение очередного уровня состоит в попарном переборе элементов списка, составляющего предыдущий (нижний) уровень. В новый уровень переносится наименьшее значение ключа из каждой пары.

Следующий этап состоит в выборке значений из пирамиды и формирования из них упорядоченной последовательности (процедура Heap_Sort и функция Competit). В каждой итерации цикла процедуры Heap_Sort выбирается значение из вершины пирамиды - это наименьшее из имеющихся в пирамиде значений ключа. Узел-вершина при этом освобождается, освобождаются также и все узлы, занимаемые выбранным значением на более низких уровнях пирамиды. За освободившиеся узлы устраивается (снизу вверх) состязание между их потомками. Так, для пирамиды, исходное состояние которой было показано на рис 3. , при выборке первых трех ключей (1, 8, 14) пирамида будет последовательно принимать вид, показанный на рис.3.14 (символом x помечены пустые места в пирамиде).

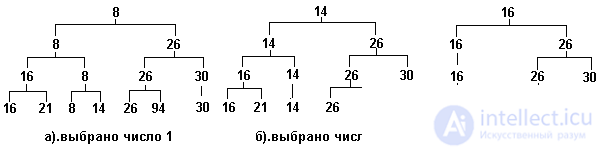
Рис.3.14. Пирамида после последовательных выборок

Процедура Heap_Sort получает входной параметр ph - указатель на вершину пирамиды. и формирует выходной параметр a - упорядоченный массив чисел. Вся процедура Heap_Sort состоит из цикла, в каждой итерации которого значение из вершины переносится в массив a, а затем вызывается функция Competit, которая обеспечивает реорганизацию пирамиды в связи с удалением значения из вершины.

Функция Competet рекурсивная, ее параметром является указатель на вершину того поддерева, которое подлежит реорганизации. В первой фазе функции устанавливается, есть ли у узла, составляющего вершину заданного поддерева, потомок, значение данных в котором совпадает со значением данных в вершине. Если такой потомок есть, то функция Competit вызывает сама себя для реорганизации того поддерева, вершиной которого является обнаруженный потомок. После реорганизации адрес потомка в узле заменяется тем адресом, который вернул рекурсивный вызов Competit. Если после реорганизации оказывается, что у узла нет потомков (или он не имел потомков с самого начала), то узел уничтожается и функция возвращает пустой указатель. Если же у узла еще остаются потомки, то в поле данных узла заносится значение данных из того потомка, в котором это значение наименьшее, и функция возвращает прежний адрес узла.

    

        
Hungry Weevils
        

          Game: Perform tasks and rest cool.6 people play!
        
        
            Play game
        
    
    

          
                   
        

    
 {===== Программный пример 3.12 =====}
 { Турнирная сортировка }
 type nptr = ^node;     { указатель на узел }
     node = record     { узел дерева }
       key : integer;     { данные }
       left, right : nptr; { указатели на потомков }
       next : nptr;        { указатель на "брата" }
       end;
 { Создание дерева - функция возвращает указатель на вершину
                     созданного дерева }
 Function Heap_Create(a : Seq) : nptr;
   var i : integer;
       ph2 : nptr;       { адрес начала списка уровня }
       p1 : nptr;        { адрес нового элемента }
       p2 : nptr;        { адрес предыдущего элемента }
       pp1, pp2 : nptr;  { адреса соревнующейся пары }
   begin
   { Фаза 1 - построение самого нижнего уровня пирамиды }
   ph2:=nil;
   for i:=1 to n do begin
     New(p1);        { выделение памяти для нового эл-та }
     p1^.key:=a[i]; { запись данных из массива }
     p1^.left:=nil; p1^.right:=nil;   { потомков нет }
     { связывание в линейный список по уровню }
     if ph2=nil then ph2:=p1 else p2^.next:=p1;
     p2:=p1;
     end; { for }
   p1^.next:=nil;
   { Фаза 2 - построение других уровней }
   while ph2^.next<>nil do begin  { цикл до вершины пирамиды }
     pp1:=ph2; ph2:=nil;          { начало нового уровня }
     while pp1<>nil do begin      { цикл по очередному уровню }
       pp2:=pp1^.next;
       New(p1);
       { адреса потомков из предыдущего уровня }
       p1^.left:=pp1; p1^.right:=pp2;
       p1^.next:=nil;
       { связывание в линейный список по уровню }
       if ph2=nil then ph2:=p1 else p2^.next:=p1;
       p2:=p1;
       { состязание данных за выход на уровень }
       if (pp2=nil)or(pp2^.key > pp1^.key) then p1^.key:=pp1^.key
       else p1^.key:=pp2^.key;
       { переход к следующей паре }
       if pp2<>nil then pp1:=pp2^.next else pp1:=nil;
       end; { while pp1<>nil }
     end; { while ph2^.next<>nil }
   Heap_Create:=ph2;
 end;
   { Реорганизация поддерева - функция возвращает 
     указатель на вершину реорганизованного дерева }
 Function Competit(ph : nptr) : nptr;
   begin
   { определение наличия потомков, выбор потомка для
     реорганизации, реорганизация его }
   if (ph^.left<>nil)and(ph^.left^.key=ph^.key) then
     ph^.left:=Competit(ph^.left)
   else if (ph^.right<>nil) then
     ph^.right:=Competit(ph^.right);
   if (ph^.left=nil)and(ph^.right=nil) then begin
     { освобождение пустого узла }
     Dispose(ph); ph:=nil;
     end;
   else
     { состязание данных потомков }
     if (ph^.left=nil) or
     ((ph^.right<>nil)and(ph^.left^.key > ph^.right^.key)) then
        ph^.key:=ph^.right^.key
      else ph^.key:=ph^.left^.key;
   Competit:=ph;
 end;
 { Сортировка }
 Procedure Heap_Sort(var a : Seq);
   var ph : nptr;   { адрес вершины дерева }
       i : integer;
   begin
   ph:=Heap_Create(a);  { создание дерева }
   { выборка из дерева }
   for i:=1 to N do begin
     { перенос данных из вершины в массив }
     a[i]:=ph^.key;
     { реорганизация дерева }
     ph:=Competit(ph);
     end;
 end;

Построение дерева требует N-1 сравнений, выборка - N*log2(N) сравнений. Порядок алгоритма, таким образом, O(N*log2(N)). Сложность операций над связными структурами данных, однако, значительно выше, чем над статическими структурами. Кроме того, алгоритм неэкономичен в отношении памяти: дублирование данных на разных уровнях пирамиды приводит к тому, что рабочая область памяти содержит примерно 2*N узлов.

Сортировка частично упорядоченным деревом.

В двоичном дереве, которое строится в этом методе сортировки для каждого узла справедливо следующее утверждение: значения ключа, записанное в узле, меньше, чем ключи его потомков. Для полностью упорядоченного дерева имеются требования к соотношению между ключами потомков. Для данного дерева таких требований нет, поэтому такое дерево и называется частично упорядоченным. Кроме того, наше дерево должно быть абсолютно сбалансированным. Это означает не только то, что длины путей к любым двум листьям различаются не более, чем на 1, но и то, что при добавлении нового элемента в дерево предпочтение всегда отдается левой ветви/подветви, пока это не нарушает сбалансированность. Более подробно деревья рассматриваются в гл.6.

Например, последовательность чисел:

              3 20 12 58 35 30 32 28

будет представлена в виде дерева, показанного на рис.3.15 .

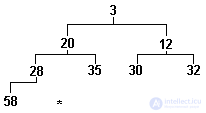
Рис.3.15. Частично упорядоченное дерево

Представление дерева в виде пирамиды наглядно показывает нам, что для такого дерева можно ввести понятия "начала" и "конца". Началом, естественно, будет считаться вершина пирамиды, а концом - крайний левый элемент в самом нижнем ряду (на рис.3.15 это 58).

Для сортировки этим методом должны быть определены две операции: вставка в дерево нового элемента и выборка из дерева минимального элемента; причем выполнение любой из этих операций не должно нарушать ни сформулированной выше частичной упорядоченности дерева, ни его сбалансированности.

Алгоритм вставки состоит в следующем. Новый элемент вставляется на первое свободное место за концом дерева (на рис.3.15 это место обозначено символом "*"). Если ключ вставленного элемента меньше, чем ключ его предка, то предок и вставленный элемент меняются местами. Ключ вставленного элемента теперь сравнивается с ключом его предка на новом месте и т.д. Сравнения заканчиваются, когда ключ нового элемента окажется больше ключа предка или когда новый элемент "выплывет" в вершину пирамиды. Пирамида, показанная на рис.3.15, построена именно последовательным включением в нее чисел из приведенного ряда. Если мы включим в нее, например, еще число 16, то пирамида примет вид, представленный на рис.3.16. (Символом "*" помечены элементы, перемещенные при этой операции.)

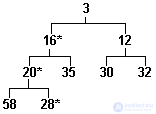
Рис.3.16. Частично упорядоченное дерево, включение элемента

Процедура выборки элемента несколько сложнее. Очевидно, что минимальный элемент находится в вершине. После выборки за освободившееся место устраивается состязание между потомками, и в вершину перемещается потомок с наименьшим значением ключа. За освободившееся место перемешенного потомка состязаются его потомки и т.д., пока свободное место не опустится до листа пирамиды. Состояние нашего дерева после выборки из него минимального числа (3) показано на рис.3.17.а.

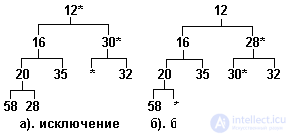
Рис.3.17. Частично упорядоченное дерево, исключение элемента

Упорядоченность дерева восстановлена, но нарушено условие его сбалансированности, так как свободное место находится не в конце дерева. Для восстановления сбалансированности последний элемент дерева переносится на освободившееся место, а затем "всплывает" по тому же алгоритму, который применялся при вставке. Результат такой балансировки показан на рис.3.17.б.

Прежде, чем описывать программный пример, иллюстрирующий сортировку частично упорядоченным деревом - пример 3.13, обратим внимание читателей на способ, которым в нем дерево представлено в памяти. Это способ представления двоичных деревьев в статической памяти (в одномерном массиве), который может быть применен и в других задачах. Элементы дерева располагаются в соседних слотах памяти по уровням. Самый первый слот выделенной памяти занимает вершина. Следующие 2 слота - элементы второго уровня, следующие 4 слота - третьего и т.д. Дерево с рис.3.17.б, например, будет линеаризовано таким образом:

               12 16 28 20 35 30 32 58

В таком представлении отпадает необходимость хранить в составе узла дерева указатели, так как адреса потомков могут быть вычислены. Для узла, представленного элементом массива с индексом i индексы его левого и правого потомков будут 2*i и 2*i+1 соответственно. Для узла с индексом i индекс его предка будет i div 2.

После всего вышесказанного алгоритм программного примера 3.13 не нуждается в особых пояснениях. Поясним только структуру примера. Пример оформлен в виде законченного программного модуля, который будет использован и в следующем примере. Само дерево представлено в массиве tree, переменная nt является индексом первого свободного элемента в массиве. Входные точки модуля:

• процедура InitST - инициализация модуля, установка начального значения nt;
• функция InsertST - вставка в дерево нового элемента; функция возвращает false, если в дереве нет свободного места, иначе - true;
• функция DeleteST - выборка из дерева минимального элемента; функция возвращает false, если дерево пустое, иначе - true;
• функция CheckST - проверка состояния дерева: ключ минимального элемента возвращается в выходном параметре, но элемент не исключается из дерева; а возвращаемое значение функции - 0 - если дерево пустое, 1 - если дерево заполнено не до конца, 2 - если дерево заполнено до конца.

Кроме того в модуле определены внутренние программные единицы:

• функция Down - обеспечивает спуск свободного места из вершины пирамиды в ее основание, функция возвращает индекс свободного места после спуска;
• процедура Up - обеспечивающая всплытие элемента с заданного места.

    

        
Hungry Weevils
        

          Game: Perform tasks and rest cool.6 people play!
        
        
            Play game
        
    
    

          
                   
        

    
 {===== Программный пример 3.13 =====}
 { Сортировка частично упорядоченным деревом }
 Unit SortTree;
 Interface
 Procedure InitSt;
 Function CheckST(var a : integer) : integer;
 Function DeleteST(var a : integer) : boolean;
 Function InsertST(a : integer) : boolean;
 Implementation
 Const NN=16;
 var tr : array[1..NN] of integer;  { дерево }
     nt : integer;     { индекс последнего эл-та в дереве }
 {** Всплытие эл-та с места с индексом l **}
 Procedure Up(l : integer);
   var h : integer; { l - индекс узла, h - индекс его предка }
       x : integer;
   begin
   h:=l div 2;   { индекс предка }
   while h > 0 do  { до начала  дерева }
     if tr[l] < tr[h] then begin { ключ узла меньше, чем у предка }
      x:=tr[l]; tr[l]:=tr[h]; tr[h]:=x; { перестановка }
      l:=h; h:=l div 2; { предок становится текущим узлом }
      end
    else h:=0; { конец всплытия }
 end;  { Procedure Up }
 {** Спуск свободного места из начала дерева **}
 Function Down : integer;
   var h, l : integer; { h - индекс узла, l - индекс его потомка }
   begin
   h:=1;    { начальный узел - начало дерева }
   while true do begin
     l:=h*2;  { вычисление индекса 1-го потомка }
     if l+1 <= nt then begin { у узла есть 2-й потомок }
       if tr[l] <= tr[l+1] then begin { 1-й потомок меньше 2-го }
         tr[h]:=tr[l]; { 1-й потомок переносится в текущ.узел }
         h:=l;  { 1-й потомок становится текущим узлом }
         end
       else begin  { 2-й потомок меньше 1-го }
         tr[h]:=tr[l+1]; { 2-й потомок переносится в текущ.узел }
         h:=l+1; { 2-й потомок становится текущим узлом }
         end;
       end
     else
       if l=nt then begin { 1-й потомок есть, 2-го нет }
         tr[h]:=tr[l]; { 1-й потомок переносится в текущ.узел }
         Down:=l;  Exit; { спуск закончен }
         end
       else begin { потомков нет - спуск закончен }
         Down:=h; Exit;
         end;
     end; { while }
 end; { Function Down }
 {** Инициализация сортировки деревом **}
 Procedure InitSt;
   begin
   nt:=0; { дерево пустое }
   end; { Procedure InitSt }
 {** Проверка состояния дерева **}
 Function CheckST(var a : integer) : integer;
   begin
   a:=tr ;   { выборка эл-та из начала }
   case nt of  { формирование возвращаемого значения функции }
     0: { дерево пустое } CheckSt:=0;
     NN: { дерево полное } CheckSt:=2;
     else { дерево частично заполнено } CheckSt:=1;
     end;
   end; {  Function CheckST }
 {** Вставка эл-та a в дерево **}
 Function InsertST(a : integer) : boolean;
   begin
   if nt=NN then { дерево заполнено - отказ } InsertST:=false
   else begin { в дереве есть место }
     nt:=nt+1; tr[nt]:=a; { запись в конец дерева }
     Up(nt);              { всплытие }
     InsertSt:=true;
     end;
   end; { Function InsertST }
 {** Выборка эл-та из дерева **}
 Function DeleteST(var a : integer) : boolean;
   var n : integer;
   begin
   if nt=0 then { дерево пустое - отказ } DeleteST:=false
   else begin { дерево не пустое }
     a:=tr ;  { выборка эл-та из начала }
     n:=Down;   { спуск свободного места в позицию n }
     if n < nt then begin
       { если свободное место спустилось не в конец дерева }
       tr[n]:=tr[nt]; { эл-т из конца переносится на своб.место }
       Up(n);         { всплытие }
       end;
     nt:=nt-1;
     DeleteSt:=true;
   end;
 end; { Function DeleteST }
 END.

Если применять сортировку частично упорядоченным деревом для упорядочения уже готовой последовательности размером N, то необходимо N раз выполнить вставку, а затем N раз - выборку. Порядок алгоритма - O(N*log2(N)), но среднее значение количества сравнений примерно в 3 раза больше, чем для турнирной сортировки. Но сортировка частично упорядоченным деревом имеет одно существенное преимущество перед всеми другими алгоритмами. Дело в том, что это самый удобный алгоритм для "сортировки on-line", когда сортируемая последовательность не зафиксирована до начала сортировки, а меняется в процессе работы и вставки чередуются с выборками. Каждое изменение (добавление/удаление элемента) сортируемой последовательности потребует здесь не более, чем 2*log2(N) сравнений и перестановок, в то время, как другие алгоритмы потребуют при единичном изменении переупорядочивания всей последовательности "по полной программе".

Типичная задача, которая требует такой сортировки, возникает при сортировке данных на внешней памяти (файлов). Первым этапом такой сортировки является формирование из данных файла упорядоченных последовательностей максимально возможной длины при ограниченном объеме оперативной памяти. Приведенный ниже программный пример (пример 3.14) показывает решение этой задачи.

Последовательность чисел, записанная во входном файле поэлементно считывается и числа по мере считывания включаются в дерево. Когда дерево оказывается заполненным, очередное считанное из файла число сравнивается с последним числом, выведенным в выходной файл. Если считанное число не меньше последнего выведенного, но меньше числа, находящегося в вершине дерева, то в выходной файл выводится считанное число. Если считанное число не меньше последнего выведенного, и не меньше числа, находящегося в вершине дерева, то в выходной файл выводится число, выбираемое из дерево, а считанное число заносится в дерево. Наконец, если считанное число меньше последнего выведенного, то поэлементно выбирается и выводится все содержимое дерева, и формирование новой последовательности начинается с записи в пустое дерево считанного числа.

 {===== Программный пример 3.14 =====}
 { Формирование отсортированных последовательностей в файле }
 Uses SortTree;
 var x : integar;   { считанное число }
     y : integer;   { число в вершине дерева }
     old : integer; { последнее выведенное число }
     inp : text;    { входной файл }
     out : text;    { выходной файл }
     bf : boolean;  { признак начала вывода последовательности }
     bx : boolean;  { рабочая переменная }
 begin
 Assign(inp,'STX.INP'); Reset(inp);
 Assign(out,'STX.OUT'); Rewrite(out);
 InitST;      { инициализация сортировки }
 bf:=false;   { вывод последовательности еще не начат }
 while not Eof(inp) do begin
   ReadLn(inp,x);  { считывание числа из файла }
   { если в дереве есть свободное место - включить в дерево }
   if CheckST(y) <= 1 then bx:=InsertST(x)
   else { в дереве нет свободного места }
     if (bf and (x < old)) or (not bf and (x < y))  then begin
       { вывод содержимого дерева }
       while DeleteST(y) do Write(out,y:3,' ');
       WriteLn(out);
       bf:=false;       { начало новой последовательности }
       bx:=InsertST(x); { занесение считанного числа в дерево }
       end
     else begin { продолжение формирования последовательности }
       if x < y then begin { вывод считанного числа }
         Write(out,x:3,' '); old:=x;
         end;
       else begin { вывод числа из вершины дерева }
         bx:=DeleteST(y);
         Write(out,y:3,' '); old:=y;
         { занесение считанного в дерево }
         bx:=InsertST(x);
         end;
       bf:=true; { вывод последовательности начался }
       end;
     end;
   Close(inp);
   { вывод остатка }
   while DeleteST(y) do Write(out,y:3,' ');
   WriteLn(out);  Close(out);
   end.

Hungry Weevils

Game: Perform tasks and rest cool.6 people play!

Play game

3.8.3. Сортировки распределением.

Поразрядная цифровая сортировка.

Алгоритм требует представления ключей сортируемой последовательности в виде чисел в некоторой системе счисления P. Число проходов сортировка равно максимальному числу значащих цифр в числе - D. В каждом проходе анализируется значащая цифра в очередном разряде ключа, начиная с младшего разряда. Все ключи с одинаковым значением этой цифры объединяются в одну группу. Ключи в группе располагаются в порядке их поступления. После того, как вся исходная последовательность распределена по группам, группы располагаются в порядке возрастания связанных с группами цифр. Процесс повторяется для второй цифры и т.д., пока не будут исчерпаны значащие цифры в ключе. Основание системы счисления P может быть любым, в частном случае 2 или 10. Для системы счисления с основанием P требуется P групп.

Порядок алгоритма качественно линейный - O(N), для сортировки требуется D*N операций анализа цифры. Однако, в такой оценке порядка не учитывается ряд обстоятельств.

Во-первых, операция выделения значащей цифры будет простой и быстрой только при P=2, для других систем счисления эта операция может оказаться значительно более времяемкой, чем операция сравнения.

Во-вторых, в оценке алгоритма не учитываются расходы времени и памяти на создание и ведение групп. Размещение групп в статической рабочей памяти потребует памяти для P*N элементов, так как в предельном случае все элементы могут попасть в какую-то одну группу. Если же формировать группы внутри той же последовательности по принципу обменных алгоритмов, то возникает необходимость перераспределения последовательности между группами и все проблемы и недостатки, присущие алгоритмам включения. Наиболее рациональным является формирование групп в виде связных списков с динамическим выделением памяти.

В программном примере 3.15 мы, однако, применяем поразрядную сортировку к статической структуре данных и формируем группы на том же месте, где расположена исходная последовательность. Пример требует некоторых пояснений.

Область памяти, занимаемая массивом перераспределяется между входным и выходным множествами, как это делалось и в ряде предыдущих примеров. Выходное множество (оно размещается в начале массива) разбивается на группы. Разбиение отслеживается в массиве b. Элемент массива b[i] содержит индекс в массиве a,с которого начинается i+1-ая группа. Номер группы определяется значением анали- зируемой цифры числа, поэтому индексация в массиве b начинается с 0. Когда очередное число выбирается из входного множества и должно быть занесено в i-ую группу выходного множества, оно будет записано в позицию, определяемую значением b[i]. Но предварительно эта позиция должна быть освобождена: участок массива от b[i] до конца выходного множества включительно сдвигается вправо. После записи числа в i-ую группу i-ое и все последующие значения в массиве b корректируются - увеличиваются на 1.

 {===== Программный пример 3.15 =====}
 { Цифровая сортировка (распределение) }
 const D=...;   { максимальное количество цифр в числе }
      P=...;   { основание системы счисления }
 Function Digit(v, n : integer) : integer;
 { возвращает значение n-ой цифры в числе v }
 begin
   for n:=n downto 2 do v:=v div P;
   Digit:=v mod P;
 end;
 Procedure Sort(var a : Seq);
   Var b : array[0..P-2] of integer; { индекс элемента,
                          следующего за последним в i-ой группе }
       i, j, k, m, x : integer;
   begin
     for m:=1 to D do begin   { перебор цифр, начиная с младшей }
     for i:=0 to P-2 do b[i]:=1; { нач. значения индексов }
     for i:=1 to N do begin   { перебор массива }
       k:=Digit(a[i],m);      { определение m-ой цифры }
       x:=a[i];
       { сдвиг - освобождение места в конце k-ой группы }
       for j:=i downto b[k]+1 do a[j]:=a[j-1];
       { запись в конец k-ой группы }
       a[b[k]]:=x;
       { модификация k-го индекса и всех больших }
       for j:=k to P-2 do b[j]:=b[j]+1;
       end;
 end;

Результаты трассировки программного примера 3.15 при P=10 и D=4 представлены в таблице 3.9.

Таблица 3.9

Быстрая сортировка Хоара.

Данный алгоритм относится к распределительным и обеспечивает показатели эффективности O(N*log2(N)) даже при наихудшем исходном распределении.

Используются два индекса - i и j - с начальными значениями 1 и N соответственно. Ключ K[i] сравнивается с ключом K[j]. Если ключи удовлетворяют критерию упорядоченности, то индекс j уменьшается на 1 и производится следующее сравнение. Если ключи не удовлетворяют критерию, то записи R[i] и R[j] меняются местами. При этом индекс j фиксируется и начинает меняться индекс i(увеличиваться на 1 после каждого сравнения). После следующей перестановки фиксируется i и начинает изменяться j и т.д. Проход заканчивается, когда индексы i и j становятся равными. Запись, находящаяся на позиции встречи индексов, стоит на своем месте в последовательности. Эта запись делит последовательность на два подмножества. Все записи, расположенные слева от нее имеют ключи, меньшие чем ключ этой записи, все записи справа - большие. Тот же самый алгоритм применяется к левому подмножеству, а затем к правому. Записи подмножества распределяются по двум еще меньшим подмножествам и т.д., и т.д. Распределение заканчивается, когда полученное подмножество будет состоять из единственного элемента - такое подмножество уже является упорядоченным.

Процедура сортировки в примере 3.16 рекурсивная. При ее вызове должны быть заданы значения границ сортируемого участка от 1 до N.

 {===== Программный пример 3.16 =====}
 { Быстрая сортировка Хоара }
 Procedure Sort(var a : Seq; i0,j0 : integer);
 { i0, j0 - границы сортируемого участка }
 Var i, j : integer;  { текущие индексы в массиве }
     flag : boolean;  { признак меняющегося индекса: если
             flag=true - уменьшается j, иначе - увеличивается i }
     x : integer;
 begin
   if j0 <= i0 Exit; { подмножество пустое или из 1 эл-та }
   i:=i0; j:=j0;
   flag:=true; { вначале будет изменяться j }
   while i < j do begin
     if a[i] > a[j] then begin
       x:=a[i]; a[i]:=a[j]; a[j]:=x; { перестановка }
       { после перестановки меняется изменяемый индекс }
       flag:= not flag;
       end;
     { реально изменяется только один индекс }
     if flag then j:=j-1 else i:=i+1;
     end;
   Sort(a,i0,i-1); { сортировка левого подмассива }
   Sort(a,i+1,j0); { сортировка правого подмассива }
 end;

Результаты трассировки примера приведены в таблице 3.10. В каждой строке таблицы показаны текущие положения индексов i и j, звездочками отмечены элементы, ставшие на свои места. Для каждого прохода показаны границы подмножества, в котором ведется сортировка.

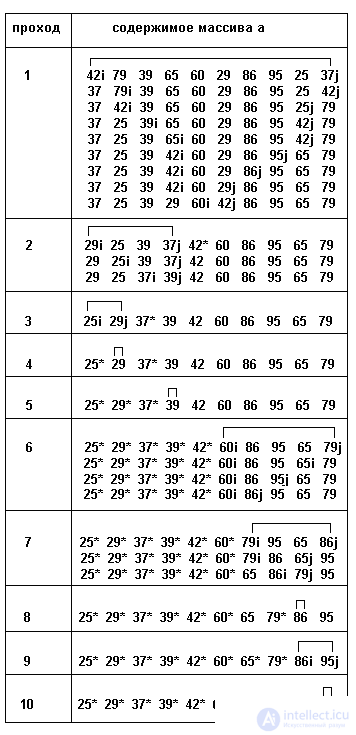
Таблица 3.10

3.8.4. Сортировки слиянием.

Алгоритмы сортировки слиянием, как правило, имеют порядок O(N*log2(N)), но отличаются от других алгоритмов большей сложностью и требуют большого числа пересылок. Алгоритмы слияния применяются в основном, как составная часть внеш- ней сортировки, которая более подробно будет рассматриваться нами во втором томе нашего пособия. Здесь же для понимания принципа слияния мы приводим простейший алгоритм слияния в оперативной памяти.

Сортировка попарным слиянием.

Входное множество рассматривается, как последовательность подмножеств, каждое из которых состоит из единственного элемента и, следовательно, является уже упорядоченным. На первом проходе каждые два соседних одно-элементных множества сливаются в одно двух-элементное упорядоченное множество. На втором проходе двух-элементные множества сливаются в 4-элементные упорядоченные множества и т.д. В конце концов мы получаем одно большое упорядоченное множество.

Важнейшей частью алгоритма является слияние двух упорядоченных множеств. Эту часть алгоритма мы опишем строго.

• 1. [Начальные установки]. Определить длины первого и второго исходных множеств - l1 и l2 соответственно. Установить индексы текущих элементов в исходных множествах i1 и i2 в 1. Установить индекс в выходном множестве j=1.
• 2. [Цикл слияния].

продолжение следует...

Продолжение:

Часть 1 3. СТАТИЧЕСКИЕ СТРУКТУРЫ ДАННЫХ
Часть 2 3.6. Таблицы как структура данных - 3. СТАТИЧЕСКИЕ СТРУКТУРЫ ДАННЫХ
Часть 3 3.8.2. Сортировки включением - 3. СТАТИЧЕСКИЕ СТРУКТУРЫ ДАННЫХ
Часть 4 Вау!! 😲 Ты еще не читал? Это зря! - 3. СТАТИЧЕСКИЕ СТРУКТУРЫ ДАННЫХ

См.также

• структуры данных , data structrures ,
• тесты по алгоритмам и структурам данных ,
• полустатические структуры данных , реализация строк ,
• стек , стеки ,
• список , односвязные списки ,
• дерево , обход дерева ,
• очереди , очередь ,
• переполнение стека , стековый кадр ,
• Круглый буфер
• Двусторонняя очередь (dequeue)
• Приоритетная очередь
• теория массового обслуживания ,
• стек , стеки ,

На этом все! Теперь вы знаете все про статические структуры данных, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое статические структуры данных, вектор структура данных, массивы структура данных, множества структура данных и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Структуры данных