Лекция
Сразу хочу сказать, что здесь никакой воды про сбалансированные деревья поиска, и только нужная информация. Для того чтобы лучше понимать что такое сбалансированные деревья поиска, деревья поиска, балансировка двоичного дерева поиска , настоятельно рекомендую прочитать все из категории Структуры данных.
Дерево поиска с минимальной высотой как раз и называется сбалансированным, т. е. таким, в котором высота левого и правого поддеревьев отличаются не более чем на единицу. Сбалансированное оно, видимо, потому что в таком дереве в среднем требуется наименьшее количество операций для поиска.
Время выполнения базовых операций в дереве поиска линейно зависит от его высоты. Но из одного и того же набора ключей можно построить разные деревья поиска , как показано на Рис. 3.
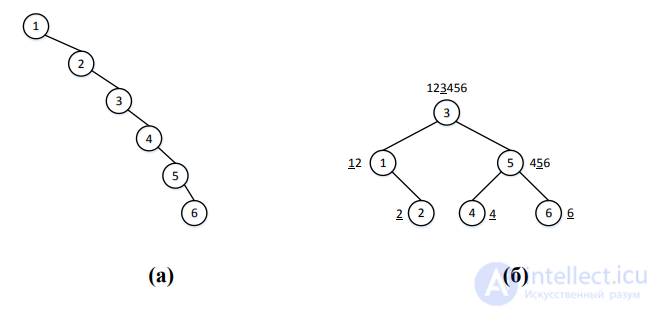
Рис. 3. Разные деревья поиска, построенные из одного и того же набора ключей
В приведенном примере на Рис. 3 оба дерева построены из одного
и того же набора ключей, но высота первого дерева больше, поэтому время выполнения операций над ним будет больше. Например, при поиске узла с ключом 6 в случае (а) требуется просмотреть все шесть узлов, а в случае (б) только три узла: 3->5->6. Второе дерево лучше сбалансировано, чем первое. В этом случае
хорошо видно преимущество двоичного дерева поиска над обычным двоичным деревом. Если бы дерево на Рис. 3(б) не было деревом поиска, то при поиске узла с ключом 6 надо было бы просмотреть от 4 до 6 узлов, в зависимости от порядка обхода дерева. А в дереве поиска при поиске узла движение происходит только вниз,
поэтому количество шагов ограничено высотой дерева. Чем больше узлов в дереве, тем более очевидно преимущество дерева поиска над обычным двоичным деревом при условии, что дерево поиска хорошо сбалансировано. Как построить дерево поиска минимальной высоты? Если набор ключей известен заранее, то его надо упорядочить. Корнем поддерева становится узел с ключом, значение которого – медиана этого набора. Для упорядоченного набора, содержащего нечетное количество ключей, – это ключ, находящийся ровно в середине набора. Для набора 1,2,3,4,5,6 из примера на Рис. 3, который содержит четное количество ключей, в качестве медианы может быть выбран ключ как со значением 3, так и со значением 4. Для определенности выберем 3. Узел с этим ключом будет корнем дерева.
Далее, ключи, меньшие 3, попадут в левое поддерево, а ключи, большие 3, попадут в правое поддерево. Для построения левого и правого поддеревьев проделываем ту же процедуру на соответствующих наборах ключей. И так до тех пор, пока все ключи не будут включены в дерево. На Рис. 3(б) для каждого узла указан набор ключей, для которых строится дерево с корнем в этом узле, и выделена медиана этого набора, которая и попадает в корень.
Дерево, изображенное на Рис. 3(б) является идеально сбалансированным, то есть, для каждого его узла количество узлов в левом и правом поддеревьях различается не более, чем на 1. Такое дерево можно построить для любого набора ключей. Достаточно заметить, что при выборе медианы на каждом шагу при построении дерева набор ключей разбивается на две части, и количество ключей в них может различаться не более, чем на 1.
Полный набор ключей не всегда известен заранее. Если ключи поступают по очереди, то построение дерева поиска будет зависеть от порядка их поступления. Если, например, ключи будут поступать в порядке 1,2,3,4,5,6, то получится дерево, изображенное на Рис. 3(а). Высота такого дерева максимальна для этого набора ключей, следовательно, и время выполнения операций над ним также будет максимальным. Поэтому при добавлении очередного узла, возможно, дерево понадобится перестраивать, чтобы уменьшить его высоту, сохраняя тот же набор узлов. Идеальную балансировку поддерживать сложно. Если при добавлении очередного узла количество узлов в левом и правом поддеревьях какого-либо узла дерева станет различаться более, чем на 1, то дерево не будет
являться идеально сбалансированным, и его надо будет перестраивать, чтобы восстановить свойства идеально сбалансированного
дерева поиска. Поэтому обычно требования к сбалансированности дерева менее строгие.
Рассмотрим три основных вида сбалансированных деревьев поиска:
Для АВЛ-деревьев сбалансированность определяется разностью высот правого и левого поддеревьев любого узла. Если эта разность по
модулю не превышает 1, то дерево считается сбалансированным. Данное условие проверяется после каждого добавления или удаления узла, и определен минимальный набор операций перестройки дерева, который приводит к восстановлению свойства сбалансированности, если оно оказалось нарушено. Об этом говорит сайт https://intellect.icu . В красно-черных деревьях каждый узел имеет дополнительное свойство – цвет, красный или черный. На дерево наложены ограничения по расположению и количеству узлов в зависимости от цвета, и определен набор операций перестройки дерева в случае нарушения этих ограничений после добавления или удаления узла. Если АВЛ-деревья накладывают достаточно строгие условия на сбалансированность, и при добавлении узлов дерево достаточно часто приходится перестраивать, то в красно-черном дереве у каждого узла высоты левого и правого поддеревьев могут отличаться не более, чем в два раза. И, наконец, третий вид рассматриваемых сбалансированных деревьев поиска – самоперестраивающиеся деревья. В отличие от двух предыдущих видов, у этих деревьев нет никаких ограничений на расположение узлов, а сбалансированность в среднем достигается за счет того, что каждый раз перед выполнением операции над узлом этот узел перемещается в корень дерева. Но есть вероятность того, что дерево может оказаться не сбалансированным, как, например, на Рис. 3(а).
АВЛ-деревом называется такое дерево поиска, в котором для любого его узла высоты левого и правого поддеревьев отличаются не более, чем на 1. Эта структура данных разработана советскими учеными Адельсон-Вельским Георгием Максимовичем и Ландисом Евгением Михайловичем в 1962 году. Аббревиатура АВЛ соответствует первым буквам фамилий этих ученых. Первоначально АВЛ-деревья были придуманы для организации перебора в шахматных программах. Советская шахматная программа «Каисса» стала первым официальным чемпионом мира в 1974 году.
В каждом узле АВЛ-дерева, помимо ключа, данных и указателей на левое и правое поддеревья (левого и правого сыновей), хранится показатель баланса – разность высот правого и левого поддеревьев. В некоторых реализациях этот показатель может вычисляться отдельно в процессе обработки дерева тогда, когда это необходимо На Рис. 4(а) приведен пример АВЛ-дерева. Таким образом, получается, что в АВЛ-дереве показатель баланса balance для каждого узла, включая корень, по модулю не превосходит 1. На Рис. 4(б) приведен пример дерева, которое не является АВЛ-деревом, поскольку в одном из узлов баланс нарушен, т.е. |balance|>1. Здесь и далее для АВЛ-деревьев будем указывать в узле значение показателя баланса.
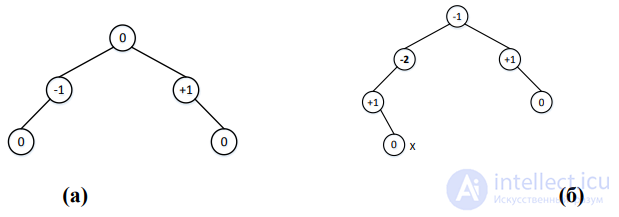
Рис. 4. (а) пример АВЛ-дерева; (б) пример дерева, не являющегося АВЛ-деревом: в узле X сбалансированность нарушена
Два крайних случая АВЛ-деревьев это: (а) совершенное дерево – все узлы имеют показатель баланса 0; (б) дерево Фибоначчи – все узлы, кроме листовых, имеют показатель баланса +1, либо все узлы, кроме листовых, имеют показатель баланса –1. Примеры приведены на Рис. 14
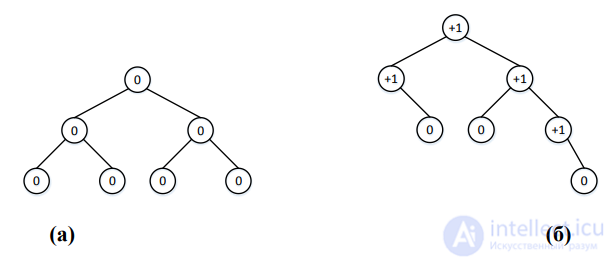
Рис. 14. Крайние случаи АВЛ-деревьев: (а) совершенное дерево; (б) дерево Фибоначчи
Не для каждого набора ключей можно построить совершенное дерево, равно как и не для каждого набора ключей можно построить дерево Фибоначчи. Но эти деревья позволяют оценить диапазон возможных высот АВЛ-деревьев. Совершенное дерево является частным случаем идеально сбалансированного дерева, поэтому оно имеет минимально возможную высоту для данного количества узлов. Дерево Фибоначчи, напротив, имеет максимально возможную высоту для данного количества узлов, при условии, что сохраняются свойства АВЛ-дерева.
основные операции для АВЛ-деревьев
АВЛ-деревья исторически были первым примером использования сбалансированных деревьев поиска. В настоящее время более популярны красно-черные деревья (КЧ-деревья). Изобретателем красно-черного дерева считается немецкий ученый Рудольф Байер. Название эта структура данных получила в статье Леонидаса Гимпаса и Роберта Седжвика 1978 года. КЧ-деревья – это двоичные деревья поиска, каждый узел которых хранит дополнительное поле color, обозначающее цвет: красный или черный, и для которых выполнены приведенные ниже свойства.
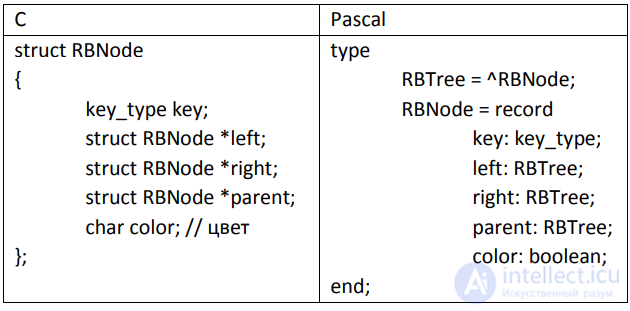
Будем считать, что если left или right равны NULL, то это «указатели» на фиктивные листья. Таким образом, все узлы – внутренние (нелистовые).
Свойства КЧ-деревьев:
1. каждый узел либо красный, либо черный;
2. каждый лист (фиктивный) – черный;
3. если узел красный, то оба его сына – черные;
4. все пути, идущие от корня к любому фиктивному листу, содержат одинаковое количество черных узлов;
5. корень – черный.
Определение 4: Черной высотой узла называется количество черных узлов на пути от этого узла к узлу, у которого оба сына – фиктивные листья.
Сам узел не включается в это число. Например, у дерева, приведенного на Рис. 15, черная высота корня равна 2.
Определение 5: Черная высота дерева – черная высота его корня.
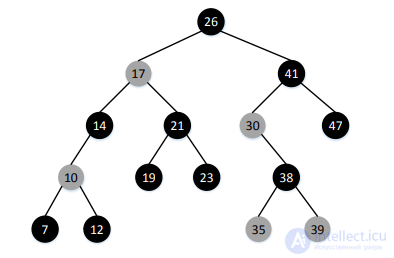
Рис. 15. Пример красно-черного дерева
основные операции для КЧ-деревьев
Самоперестраивающееся дерево – это двоичное дерево поиска, которое, в отличие от предыдущих двух видов деревьев не содержит дополнительных служебных полей в структуре данных (баланс, цвет и т.п.). Оно позволяет находить быстрее те данные, которые использовались недавно. Самоперестраивающееся дерево
было придумано Робертом Тарьяном и Даниелем Слейтером в 1983 году.
Идея самоперестраивающихся деревьев основана на принципе перемещения найденного узла в корень дерева. Эта операция называется splay(T, k), где k – это ключ, а T – двоичное дерево поиска.
После выполнения операции splay(T, k) двоичное дерево T перестраивается, оставаясь при этом деревом поиска, так, что:
Таким образом, поиск узла в самоперестраивающемся дереве фактически сводится к выполнению операции splay. Эвристика moveto-front (перемещение найденного узла в корень) основана на предположении, что если тот же самый элемент потребуется в ближайшее время, он будет найден быстрее.
Определение 6: Словарными операциями над деревом называются базовые операции: поиск, вставка и удаление.
основные операции
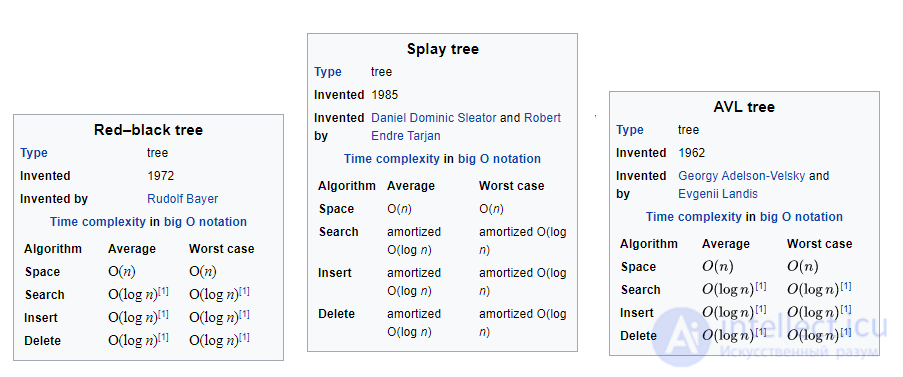
В общем случае сравнение трех рассмотренных типов деревьев провести затруднительно, поскольку для разных задач и разных наборов данных лучший тип дерева может быть разным. Сравнивать деревья можно по разным критериям: по сложности реализации, в теории, на практике.
По сложности реализации самые простые – АВЛ-дерево, самые сложные – КЧ-деревья, поскольку приходится рассматривать много нетривиальных случаев при вставке и удалении узла. В теории оценки сверху для всех трех типов деревьев примерно одинаковые. Восстановление свойств как АВЛ-дерева, так и КЧ-дерева после вставки требует не более двух поворотов. Но после удаления узла из КЧ-дерева потребуется не более трех поворотов, а в АВЛ-дереве после удаления узла может потребоваться количество поворотов до высоты дерева (от листа до корня). Поэтому операция удаления в КЧ-дереве эффективнее, в связи с чем они
больше распространены.
Самоперестраивающиеся деревья существенно отличаются от АВЛ- и КЧ-деревьев потому как не накладываются никакие ограничения на структуру дерева. Операция поиска в дереве модифицирует само дерево, поэтому в случае обращения к разным узлам самоперестраивающееся дерево может работать медленнее. К тому же, в процессе работы дерево может оказаться полностью разбалансированным. Но доказано, что если вероятности обращения к узлам фиксированы, то самоперестраивающееся дерево будет работать асимптотически не медленнее двух других рассмотренных видов деревьев . Отсутствие дополнительных полей дает преимущество по памяти.
Различные виды сбалансированных деревьев поиска используются, в частности, в системном программном обеспечении, например, в ядрах операционных систем. В статье приведены результаты тестов, имитирующих некоторую реальную нагрузку на деревья поиска. Учитывая, что таблицы виртуальных адресов в Linux часто делаются на двоичных деревьях поиска, авторы инструментировали несколько приложений, чтобы получить последовательность их обращений к подсистемам виртуальной памяти, а затем использовали эти последовательности для эмуляции нагрузки на двоичные деревья в ядре операционной системы. Так, например, показано, что если при использовании браузером Mozilla виртуальной памяти менеджер виртуальной памяти будет использовать самоперестраивающиеся деревья, то преимущество этого вида деревьев по времени работы над АВЛ- и КЧ-деревьями будет минимум в 2, а максимум в 3.4 раза.
В статье также показано, в каком случае какой вид деревьев лучше всего использовать. Если входные данные полностью рандомизированы, то наилучшим вариантом оказываются деревья поиска общего вида – несбалансированные. Если входные данные в основном рандомизированные, но периодически встречаются упорядоченные наборы, то стоит выбрать КЧ-деревья. Если при вставке преобладают упорядоченные данные, то АВЛ-деревья оказываются лучше в случае, когда дальнейший доступ к элементам рандомизирован, а самоперестраивающиеся деревья – когда дальнейшие доступ последователен или кластеризован.
А как ты думаешь, при улучшении сбалансированные деревья поиска, будет лучше нам? Надеюсь, что теперь ты понял что такое сбалансированные деревья поиска, деревья поиска, балансировка двоичного дерева поиска и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Структуры данных
Комментарии
Оставить комментарий
Структуры данных
Термины: Структуры данных