Лекция
Привет, сегодня поговорим про простые структуры данных, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое простые структуры данных, представление простых типов в памяти , настоятельно рекомендую прочитать все из категории Структуры данных.
Различные структуры данных имеют разное машинное представление, особенно базовые (простые) структуры, из которых строятся более сложные конструкции данных.
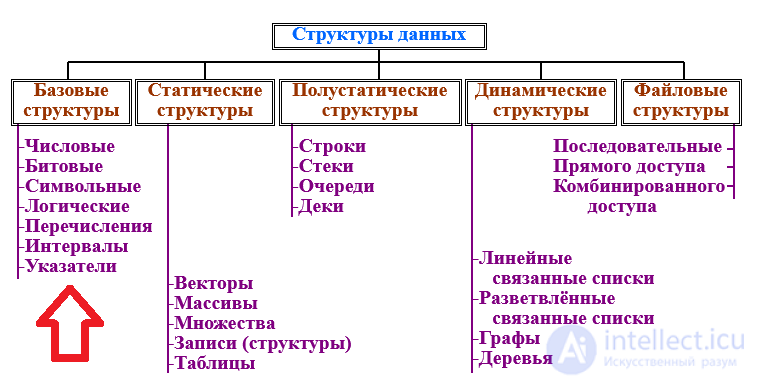
Простые структуры данных называют также примитивными или базовыми структурами. Эти структуры служат основой для построения более сложных структур. В языках программирования простые структуры описываются простыми (базовыми) типами. К таким типам относятся: числовые, битовые, логические, символьные, перечисляемые, интервальные, указатели. Структура простых типов многих языков программирования включая Си, приведена на рис 2.1 (через запятую указан размер памяти в байтах, требуемый для размещения данных соответствующего типа). В других языках программирования набор простых типов может несколько отличаться от указанного. Размер же памяти, необходимый для данных того или иного типа, может быть разным не только в разных языках программирования, но и в разных реализациях одного и того же языка.
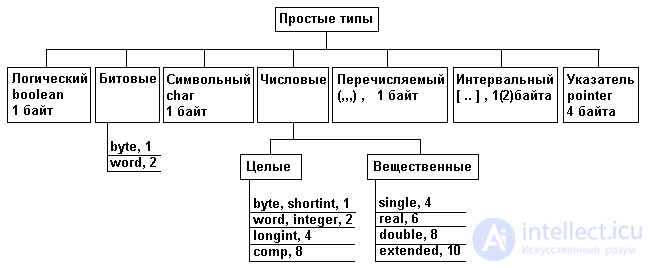

Рис. 2.1. Структура простых типов .
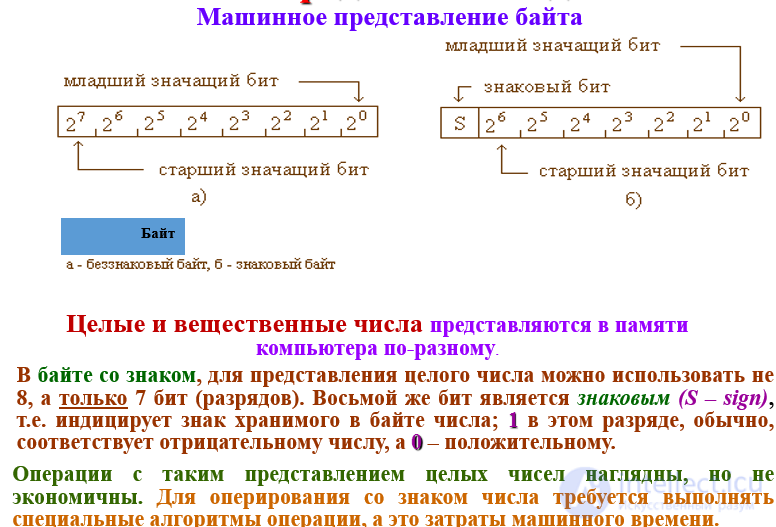
Более экономным является представление отрицательных целых чисел в дополнительном коде, который формируется следующим образом:

Для положительных чисел прямой, обратный и дополнительный коды одинаковы, при этом знаковый (старший) разряд равен 0. Аналогично представляются целые числа других типов.

С помощью целых чисел может быть представлено количество объектов, являющихся дискретными по своей природе (т.е. счетное число объектов).
Представление в памяти.
Для представления чисел со знаком в ряде компьютеров был использован метод, называемый методом знака и значения. Обычно для знака отводится первый (или самый левый) бит двоичного числа затем следует запись самого числа.
Например, +10 и -15 в двоичном виде можно представить так:
| Число | Знаковый бит | Величина |
| +10 | 0 | 0001010 |
| -15 | 1 | 0001111 |
Отметим, что по соглашению 0 используется для представления знака плюс и 1 - для минуса. Такое представление удобно для программистов т.к. легко воспринимается, но не является экономичным.

Если требуется сложить или вычесть два числа, то для решения вопроса о том, какие действия следует при этом предпринять, надо сначала определить знак каждого числа. Например, сложение чисел +6 и -7 на самом деле подразумевает операцию вычитания, а вычитание -6 из +7 операцию сложения. Для анализа знакового бита требуется особая схема и, кроме того, при представлении числа в виде знака и величины необходимы отдельные устройства для сложения и вычитания, т.е., если положительное и отрицательные числа представлены в прямом коде, операции над кодами знаков выполняются раздельно. Поэтому представление чисел в виде знака и значения не нашло широкого применения.
В то же время, при помощи обратного и дополнительного кодов, используемых для представления отрицательных чисел, операция вычитания (алгебраического сложения) сводится к операции простого арифметического сложения. При этом операция сложения распространяется и на разряды знаков, рассматриваемых как разряды целой части числа. Именно поэтому для представления целых чисел со знаком применяется дополнительный код.
Дополнительный код отрицательного числа формируется по следующим правилам:
Например, для числа -33 в формате integer:
1000000000100001 прямой код
0111111111011110 обратный код
+_______________1
1111111111011111 дополнительный код
Для положительных чисел прямой, обратный и дополнительный коды одинаковы. Аналогично представляются целые числа в формате shortint, longint, comp.
При разработке программ на этапе выбора типа данных важно знать диапазон целых величин, которые могут храниться в n разрядах памяти. В соответствии с алгоритмом преобразования двоичных чисел в десятичные, формула суммирования для n разрядов имеет вид:
n-1
2^0 + 2^1 + 2^3 + ... + 2^(n-1), или СУММА (2^i) = 2^n - 1.
i=0
При n-битовом хранении числа в дополнительном коде первый бит выражает знак целого числа. Поэтому положительные числа представляются в диапазоне от 0 до 1*2^0 + 1*2^1 +...+ 1*2^(n-2) или от 0 до 2^(n-1) - 1. Все другие конфигурации битов выражают отрицательные числа в диапазоне от -2^(n-1) до -1. Таким образом, можно сказать, что число N может храниться в n разрядах памяти, если его значение находится в диапазоне:
-2^(n-1) <= N <= 2^(n-1) - 1.
| Тип | Диапазон значений | Машинное представление |
| shortint | -128..127 | 8 бит, со знаком |
| integer | -32768..32767 | 16 бит, со знаком |
| longint | -2147483648..2147483647 | 32 бита, со знаком |
| byte | 0..255 | 8 бит, без знака |
| word | 0..65535 | 16 бит, без знака |
| comp | -2^63+1..2^63-1 | 64 бита, со знаком |
Таблица 2.1
Иными словами, диапазон возможных значений целых типов зависит от их внутреннего представления, которое может занимать 1, 2 или 4 байта. В таблице 2.1 приводится перечень целых типов, размер памяти для их внутреннего представления в битах, диапазон возможных значений.
Машинное представление беззнаковых типов.
К беззнаковым типам в PASCAL относятся типы BYTE и WORD.
Формат машинного представления чисел типа BYTE приведен на рис 2.2. а).
Например: 1). Машинное представление числа 45:
45=2^5+2^3+2^2+2^0 = 00101101
2). Машинное представление границ диапазона
допустимых значений чисел 0 и 255:
0: 00000000; 255: 11111111.
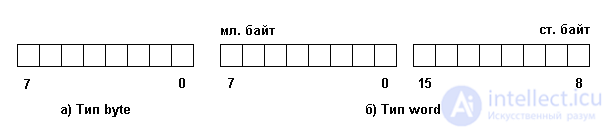
Рис. 2.2. Формат машинного представления беззнаковых чисел
Формат машинного представления чисел типа WORD приведен на рис. 2.2. б).
Например: 1). Машинное представление числа 258:
257=2^8+2^1 = 00000010 00000001.
2). Машинное представление границ:
0: 00000000 00000000; 65535: 11111111 11111111.
Для представления чисел со знаком определены следующие типы SHORTINT, INTEGER, LONGINT. В приведенных типах числа хранятся в дополнительном ко- де. Напомним, что дополнительный код положительных чисел совпадает с прямым кодом.
Формат машинного представления чисел типа SHORTINT приведен на рис 2.3. а) где s-знаковый разряд числа. Для положительных чисел s=0, для отрицательных s=1.
Например, машинное представление чисел в формате shortint:
1). 0: 00000000;
2). +127: 01111111;
3). -128: 10000000.
Формат машинного представления чисел типа INTEGER приведен на рис 2.3. б). Например:
1). +32765: 11111101 01111111;
2). -32765: 00000011 10000000;
3). -47: 11010001 11111111.
Машинное представление границ диапазона допустимых значений:
4). -32768: 00000000 10000000;
5). 32767: 11111111 01111111.
Формат машинного представления чисел типа LONGINT приведен на рис 2.3. в). Например, представление чисел в формате longint:
1). +89 01011001 00000000 00000000 00000000;
2). -89 10100111 11111111 11111111 11111111.
Машинное представление данных типа COMP. . 0 Тип COMP предназначен для работы с большими целыми числами (см. таблицу 2.1). Поэтому числа данного типа представляются в памяти в соответствии с правилами представления целых чисел со знаком - в дополнительном коде. Но для удобства пользователей при вводе и выводе значений чисел в этом формате допускается использование формы записи чисел характерных для вещественных чисел (в виде мантиссы и порядка).
Например: машинное представление чисел в формате COMP:
+512 0..0 00000010 0..0 0..0 0..0 0..0 0..0 0..0
-512 0..0 11111110 1..1 1..1 1..1 1..1 1..1 1..1
В отличии от порядковых типов (все целые, символьный, логический), значения которых всегда сопоставляются с рядом целых чисел и, следовательно, представляются в памяти машины абсолютно точно, значение вещественных типов определяет число лишь с некоторой конечной точностью, зависящей от внутреннего формата вещественного числа.
В некоторых областях вычислений требуются очень большие или весьма малые действительные числа. Для получения большей точности применяют запись чисел с плавающей точкой. Запись числа в формате с плавающей точкой является весьма эффективным средством представления очень больших и весьма малых вещественных чисел при условии, что они содержат ограниченное число значащих цифр, и, следовательно, не все вещественные числа могут быть представлены в памяти. Обычно число используемых при вычислениях значащих цифр таково, что для большинства задач ошибки округления пренебрежимо малы.
Система вещественных чисел, применяемая при ручных вычислениях, предполагается бесконечно непрерывной. Это означает, что не существует никаких ограничений на диапазон используемых чисел и точность их представления. Для любого вещественного числа имеется бесконечно много чисел, которые больше или меньше его, а между любыми двумя вещественными числами также находится бесконечно много вещественных чисел.
Реализовать такую систему в технических устройствах невозможно. Во всех компьютерах размеры ячеек памяти фиксированы, что ограничивает систему представимых чисел. Ограничения касаются как диапазона, так и точности представления чисел, т.е. система машинных чисел оказывается конечной и и дискретной, образуя подмножество системы вещественных чисел.
Отсюда, в отличии от порядковых типов (все целые, символьный, логический), значения которых всегда сопоставляются с рядом целых чисел и, следовательно, представляются в памяти машины абсолютно точно, значение вещественных типов определяет число лишь с некоторой конечной точностью, зависящей от внутреннего формата вещественного числа.
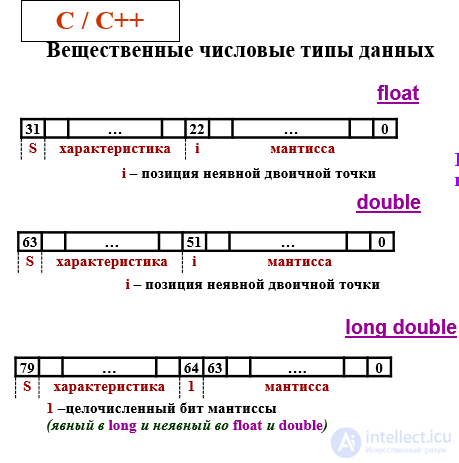
Для вещественных чисел по стандарту ANSI/IEEE 754-1985 (IEEE Standard for Binary Floating-Point Arithmetic’s) используется нормализованное представление со смещенным порядком. То есть число приводится к виду:
A = ±M · 2±P, ½ <= M < 1,
где M – мантисса, P – порядок. (Нормализованная запись отличного от нуля действительного числа – это запись вида a = m*Qp, где p – целое число (положительное, отрицательное или ноль), а m – правильная Q-ричная дробь, у которой первая цифра после запятой не равна нулю, то есть 1/Q <= m <1). Так как в результате старший разряд целой части двоичного числа всегда равен единице, его обычно в памяти не хранят («скрытый бит» или «скрытая единица»). Порядок хранится в смещенном коде («модифицированный порядок» или «характеристика»):
P' = P+2n-1, где n – число разрядов машинного представления порядка. Это делается для того, чтобы характеристика всегда была положительной. Для представления нуля обнуляются все биты мантиссы и порядка.
Объясним ИНАЧЕ: Старший разряд двоичного представления вещественного числа всегда кодирует знак числа. Остальная часть разбивается на две части: мантиссу и экспоненту. Вещественное число имеет вид:
A = ±S · M · 2E,
где S - знаковый бит числа, E - экспонента, M - мантисса. Если 1/2≤M<1, то такое число называется нормализованным. При хранении нормализованных чисел сопроцессор отбрасывает целую часть мантиссы (она всегда 1), сохраняя лишь дробную часть. Экспонента кодируется со сдвигом на половину разрядной сетки, таким образом, удается избежать вопроса о кодировании знака экспоненты. Т.е. при 8-битной разрядности экспоненты код 0 соответствует числу -127, 1 - числу -126, ..., 255 числу +126 (экспонента вычисляется как код 127).
Формат для представления чисел с плавающей точкой содержит одно или два поля фиксированной длины для знаков. Количество позиций для значащих цифр различно в разных ЭВМ, но существует, тем не менее, общий формат, приведенный на рисунке 2.5 а). В соответствии с этой записью формат вещественного числа содержит в общем случае поля мантиссы, порядка и знаков мантиссы и порядка.

Рис. 2.5. Формат представления вещественных чисел
Однако, чаще вместо порядка используется характеристика, получающаяся прибавлением к порядку такого смещения, чтобы характеристика была всегда положительный. При этом имеет место формат представления вещественных чисел такой, как на рис 2.5 б).
Введение характеристики избавляет от необходимости выделять один бит для знака порядка и упрощает выполнение операций сравнения (<,>,<=,>=) и арифметических операций над вещественными числами. Так, при сложении или вычитании чисел с плавающей точкой для того, чтобы выровнять операнды, требуется сдвиг влево или вправо мантиссы числа. Сдвиг можно осуществить с помощью единственного счетчика, в который сначала заносится положительное чис- ло, уменьшающееся затем до тех пор, пока не будет выполнено требуемое число сдвигов.
Таким образом, для представления вещественных чисел в памяти ЭВМ порядок p вещественного числа представляется в виде характеристики путем добавления смещения (старшего бита порядка):
Х = 2^(n-1) + k + p, (2.1)
где:
Формулы для вычисления характеристики и количество бит, необходимых для ее хранения, приведены в таблице 2.2.
| Тип | Харрактеристика | Кол-во бит на хар-ку |
| real | x = 2^7 + p + 1 | 8 |
| single | x = 2^7 + p - 1 | 8 |
| double | x = 2^10 + p - 1 | 11 |
| extended | x = 2^14 + p - 1 | 15 |
Таблица 2.2
Следующим компонентом представляемого в машине числа с плавающей точкой является мантисса. Для увеличения количества значащих цифр в представлении числа и исключения переполнения при умножении мантиссу обычно подвергают нормализации. Нормализация означает, что мантисса (назовем ее F), кроме случая, когда F=0, должна находиться в интервале
R^(-1) <= F < 1.
Для двоичной системы счисления R=2. Тогда в связи с тем, что 2^(-1) <= F < 1, ненулевая мантисса любого хранимого числа с плавающей точкой должна начинаться с двоичной единицы. В этом и заключается одно из достоинств двоичной формы представления числа с плавающей точкой. Поскольку процесс нормализации создает дробь, первый бит которой равен 1, в структуре некоторых машин эта еди- ница учитывается, однако не записывается в мантиссу. Эту единицу часто называют скрытой единицей, а получающийся дополнительный бит используют для увеличения точности представления чисел или их диапазона.
Приведенный метод нормализации является классическим методом, при котором результат нормализации представляется в виде правильной дроби, т.е. с единицей после точки и нулем в целой части числа. Но нормализацию мантиссы можно выполнить по разному.
В IBM PC нормализованная мантисса содержит свой старший бит слева от точки. Иными словами нормализованная мантисса в IBM PC принадлежит интервалу 1 <= F < 2. В памяти машины для данных типа real, single, double этот бит не хранится, т.е. является "скрытым" и используется для увеличения порядка в форматах single или для хранения знака в формате real. Для положительных и отрицательных чисел нормализованная мантисса в памяти представлена в прямом коде.
Первый, старший, бит в представлении чисел в формате с плавающей точкой является знаковым, и по принятому соглашению нуль обозначает положительное число, а единица - отрицательное.
Число бит для хранения мантиссы и порядка зависит от типа вещественного числа. Суммарное количество байтов, диапазоны допустимых значений чисел вещественных типов, а также количество значащих цифр после запятой в представлении чисел приведены в таблице 2.3.
| Тип | Диапазон значений | Значащие цифры | Размер в байтах |
| real | 2.9*10^(-39)..1.7*10^38 | 11-12 | 6 |
| single | 1.4*10^(-45)..3.4*10^38 | 7-8 | 4 |
| double | 4.9*10^(-324)..1.8*10^308 | 15-16 | 8 |
| extended | 3.1*10^(-4944)..1.2*10^4932 | 19-20 | 10 |
Таблица 2.3

Алгоритм формирования состоит из следующих пунктов:
Машинное представление данных типа REAL
Формат машинного представления данных типа REAL следующий:
мл. байт ст. байт
а: 7 0 15 8 23 16 31 24 39 32 47 40
x....x м....м м....м м....м м....м sм...м
б: 7 0 -32 -39 -24 -31 -16 -23 -8 -15 -1 -7
где:
Например:
1). Десятичное число 15.375;
в двоичной системе счисления 1111.011;
результат нормализации 1.111011*2^3; р=3.
Учитывая отбрасывание неявной единицы и сдвиг порядка, получаем: s=0; х=2^7+1+3=2^7+2^2=132;
в двоичной системе счисления х=10000100; м=1110110...0;
машинное представление числа:
10000100 00000000 00000000 00000000 00000000 01110110
2). Десятичное число -0.5;
аналогичные выкладки дают: нормализованную мантиссу: 1.00...0;
машинное представление числа:
10000000 00000000 00000000 00000000 00000000 10000000
3). Десятичное число -25.75;
аналогично: нормализованная мантисса: 1.10011100...0;
машинное представление числа:
10000101 00000000 00000000 00000000 00000000 11001110
4). Число 0.0;
Машинное представление числа:
00000000 00000000 00000000 00000000 00000000 00000000
5). Числа верхней и нижней границ положительного диапазона
~1.7*10^38 -
11111111 11111111 11111111 11111111 11111111 01111111
~2.9*10^(-35) -
00000001 00000000 00000000 00000000 00000000 00000000
Машинное представление данных типа SINGLE
Формат машинного представления данных типа SINGLE следующий:
мл. байт ст. байт
7 0 15 8 23 22 16 31 30 24 - номера разрядов памяти
м....м м....м х м...м s х...х
-16 -23 -8 -15 0 -1 -7 7 1 - показатели степеней разрядов
мантиссы и характеристики
где:
Например:
1). Число -15.375;
в двоичной системе счисления -1111.011;
нормализованное двоичное число -1.111011*2^3; р=3.
Учитывая отбрасывание неявной единицы и сдвиг порядка, получаем: s=1; х=2^7-1+3=2^7+2^1=130;
в двоичной системе счисления х=10000010; м=1110110...0;
машинное представление числа в формате SINGLE:
00000000 00000000 01110110 11000001
2). Число -0.1875;
в двоичной системе счисления -0.0011;
нормализованное двоичное число -1.1*2^(-3); р=-3.
Учитывая отбрасывание неявной единицы и сдвиг порядка, получаем: s=1; х=2^7-1-3=2^7-2^2;
в двоичной системе счисления х=01111100; м=100...0;
машинное представление числа в формате SINGLE:
00000000 00000000 01000000 10111110
3). Десятичное число 4.5;
аналогичные выкладки дают нормализованную мантиссу: 1.00100...0;
машинное представление числа:
00000000 00000000 10010000 01000000
4). Значения верхней и нижней границ чисел отрицательного диапазона
~-3.4*10^38 - 11111111 11111111 01111111 11111111 ~-.4*10^(-45) - 00000001 00000000 00000000 10000000
Машинное представление данных типа DOUBLE
Формат машинного представления данных типа DOUBLE следующий:
мл.байт ст.байт 7 0 15 8 23 16 31 24 39 32 47 40 55 52 51 48 63 56 м...м м...м м...м м...м м...м м...м х..х м...м s x..x -44 -50 -37 -43 -29 -36 -21 -28 -13 -20 -5 -12 3 0 -1 -4 10 4
где:
Например:
1). Число 15.375;
в двоичной системе счисления 1111.011;
результат нормализации 1.111011*2^3; р=3.
Учитывая отбрасывание скрытой единицы и сдвиг порядка, получаем: s=0; x=2^10-1+3=2^10+2^1=1026;
в двоичной системе счисления х=10000000010; m=1110110...0;
машинное представление числа в формате DOUBLE:
0 00000000 00000000 00000000 00000000 31
32 00000000 11000000 00101110 01000000 63
2). Десятичное число 0.0375;
в двоичной системе счисления 0.011;
результат нормализации 1.1*2^(-2); р=-2.
Учитывая отбрасывание скрытой единицы и сдвиг порядка, получаем: s=0; x=2^10-2^1-2^0=2^10-3;
в двоичной системе счисления х=01111111101; m=100...0;
машинное представление числа в формате DOUBLE:
0 00000000 00000000 00000000 00000000 31
32 00000000 00000000 11011000 00111111 63
3). Десятичное число 2.5;
аналогичные выкладки дают нормализованную мантиссу: 1.0100...0;
машинное представление числа 2.5:
00000000 00000000 00000000 00000000
00000000 00000000 00000100 01000000
4). Значения верхней и нижней границ диапазона положительных чисел:
~1.8*10^308 - 11111111 11111111 11111111 11111111
11111111 11111111 11101111 01111111
~4.9*10^(-324) - 00000001 00000000 00000000 00000000
00000000 00000000 00000000 00000000
Символ ~ обозначает приближенное значение числа.
Машинное представление данных типа EXTENDED
Формат машинного представления данных типа EXTENDED следующий:
мл.байт ст. байт 7 0 15 8 23 16 31 24 39 32 47 40 55 48 63 56 71 64 79 72 м..м м..м м..м м..м м..м м..м м..м м..м х..х sх..х -56-63-48-55-40-47-32-39-24-31-16-23-8 -15 0 -7 7 0 14 8
где:
Например:
1). Число -15.375;
в двоичной системе счисления -1111.011;
после нормализации -1.111011*2^3; р=3.
Учитывая присутствие скрытой единицы и сдвиг порядка, получаем: s=1; х=2^14-1+3=2^14+2^1=16386;
в двоичной системе счисления х=100000000000010; м=11110110...0
(в мантиссе единица стоящая слева от запятой не отбрасывается).
Машинное представление данного числа в формате EXTENDED:
0..0 0..0 0..0 0..0 0..0 0..0 0..0 11110110 00000010 11000000
2). Число 1.0;
аналогичные выкладки дают
нормализованную мантиссу: 1.0...0;
машинное представление числа 1.0:
0..0 0..0 0..0 0..0 0..0 0..0 0..0 10000000 11111111 00111111
3). Значения верхней и нижней границ диапазона положительных чисел
(символом * помечены разряды, значения которых при данной характеристике не идентифицируются т. е. их значения не влияют на значение мантиссы):
~1.2*10^4932 - ******** ******** 11111111 11111111 11111111
11111111 11111111 11111111 11111111 011111111
~3.1*10^4944 - ******** ******** 00000001 00000000 000000000
00000000 00000000 00000000 00000001 000000000
2.1.3. Десятичные типы
Десятичные типы не поддерживаются языком PASCAL, но имеются в некоторых других языках, например, COBOL, PL/1. Эти типы приме няются для внутримашинного представления таких данных, которые в первую очередь должны храниться в вычислительной системе и выдаваться пользователю по требованию, и лишь во вторую очередь - обрабатываться (служить операндами вычислительных операций). Неслучайно эти типы впервые появились в языке COBOL, ориентированном на обработку экономической информации: в большинстве задач этой сферы важно прежде всего хранить и находить информацию, а ее преобразование выполняется сравнительно редко и сводится к простейшим арифметическим операциям.
Архитектура некоторых вычислительных систем (например, IBM System/390) предусматривает команды, работающие с десятичным представлением чисел, хотя эти команды и выполняются гораздо медленнее, чем команды двоичной арифметики. В других архитектурах операции с десятичными числами моделируются программно.
К десятичным типам относятся: десятичный тип с фиксированной точкой и тип шаблона.
Десятичный тип с фиксированной точкой.
В языке PL/1 десятичный тип с фиксированной точкой описывается в программе, как:
DECIMAL FIXED (m.d) или DECIMAL FIXED (m).
Первое описание означает, что данное представляется в виде числа, состоящего из m десятичных цифр, из которых d цифр расположены после десятичной точки. Второе - целое число из m десятичных цифр. Следует подчеркнуть, что в любом случае число десятичных цифр в числе фиксировано. Внутримашинное представление целых чисел и чисел с дробной частью одинаково. Для последних положение десятичной точки запоминается компилятором и учитывается им при трансляции операций, в которых участвуют десятичные числа с фиксированной точкой.
Внутримашинное представление данного типа носит название десятичного упакованного формата. Примеры представления чисел в таком формате приведены на рис. 2.6.
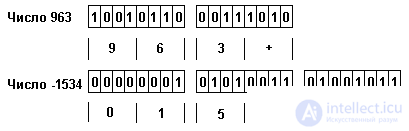
Рис.2.6. Машинное представление десятичных чисел в упакованном формате
Каждая десятичная цифра числа занимает полбайта (4 двоичных разряда) и представляется в этом полубайте ее двоичным кодом. Еще полбайта занимает знак числа, который представляется двоичным кодом 1010 - знак "+" или 1011 - знак "-". Представление занимает целое число байт и при необходимости дополняется ведущим нулем.
Тип шаблона.
В языке PL/1 тип шаблона описывается в программе, как: PICTURE '9...9'.
Это означает, что данное представляет собой целое число, содержащее столько цифр, сколько девяток указано в описании.
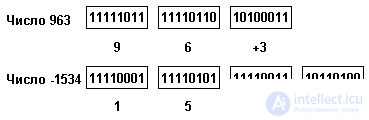
Рис.2.7. Машинное представление десятичных чисел в зонном формате
Внутримашинное представление этого типа, так называемый десятичный зонный формат, весьма близок к такому представлению данных, которое удобно пользователю: каждая десятичная цифра представляется байтом: содержащим код символа соответствующей цифры. В IBM System/390, которая аппаратно поддерживает зонный формат, применяется символьный код EBCDIC, в котором код символа цифры содержит в старшем полубайте код 1111, а в младшем - двоичный код цифры числа. Знак не входит в общее число цифр в числе, для представления знака в старшем полубайте последней цифры числа код 1111 заменяется на 1010 - знак "+" или 1011 - знак "-".
Примеры представления чисел в зонном формате приведены на рис.2.7.
Над числовыми типами, как и над всеми другими, возможны прежде всего четыре основных операции: создание, уничтожение, выбор, обновление. Специфические операции над числовыми типами - хорошо известные всем арифметические операции: сложение, вычитание, умножение, деление. Операция возведения в степень в некоторых языках также является базовой и обозначается специальным символом или комбинацией символов (^ - в BASIC, ** - в PL/1), в дру- гих - выполняется встроенными функциями (pow в C).
Обратим внимание на то, что операция деления по-разному выполняется для целых и вещественных чисел. При делении целых чисел дробная часть результата отбрасывается, как бы близка к 1 она ни была. В связи с этим в языке PASCAL имеются даже разные обозначения для деления вещественных и целых чисел - операции "/" и "div" соответственно. В других языках оба вида деления обозначаются одинаково, а тип деления определяется типом операндов. Для целых операндов возможна еще одна операция - остаток от деления - ("mod" - в PASCAL, "%" - в C).
Еще одна группа операций над числовыми типами - операции сравнения: "равно", "не равно", "больше", "меньше" и т.п. Существенно, что хотя операндами этих операций являются данные числовых типов, результат их имеет логический тип - "истина" или "ложь".Говоря об операциях сравнения, следует обратить внимание на особенность выполнения сравнений на равенство/неравенство вещественных чисел. Поскольку эти числа представляются в памяти с некоторой (не абсолютной) точностью, сравнения их не всегда могут быть абсолютно достоверны.
Поскольку одни и те же операции допустимы для разных числовых типов, возникает проблема арифметических выражений со смешением типов. Это создает некоторые неудобства для программистов, так как в реальных задачах выражения со смешанными типами встречаются довольно часто. Поэтому большинство языков допускает выражения, операнды которых имеют разные числовые типы, но обрабаты- ваются такие выражения в разных языках по-разному. В языке PL/1, например, все операнды выражения приводятся к одному типу - к типу той переменной, в которую будет записан результат, а затем уже выражение вычисляется. В языке же C преобразование типов выполняется в процессе вычисления выражения, при выполнении каждой отдельной операции, без учета других операций; каждая операция вычисляется с точностью самого точного участвующего в ней операнда. Программист, использующий выражения со смешением типов, должен точно знать правила их вычисления для выбранного языка.
Представление битовых типов.
В ряде задач может потребоваться работа с отдельными двоичными разрядами данных. Чаще всего такие задачи возникают в системном программировании, когда, например, отдельный разряд связан с состоянием отдельного аппаратного переключателя или отдельной шины передачи данных и т.п. Данные такого типа представляются в виде набора битов, упакованных в байты или слова, и не связанных друг с другом. Операции над
продолжение следует...
Часть 1 2. ПРОСТЫЕ СТРУКТУРЫ ДАННЫХ и представление их в памяти компьютера
Часть 2 2.3. Логический тип - 2. ПРОСТЫЕ СТРУКТУРЫ ДАННЫХ и представление
Комментарии
Оставить комментарий
Структуры данных
Термины: Структуры данных