Лекция
Привет, сегодня поговорим про красно-черное, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое красно-черное, дерево поиска , настоятельно рекомендую прочитать все из категории Структуры данных.
красно-черное дерево это особый тип двоичного дерева, используемый для поиска данных, таких как фрагменты текста или числа.
Листовые узлы красно-черных деревьев не содержат данных. Такие листья не нуждаются в явном выделении памяти — нулевой указатель на потомка может фактически означать, что этот потомок — листовой узел, но в некоторых случаях работы с красно-черными деревьями использование явных листовых узлов может послужить упрощением алгоритма.
Бинарные деревья поиска высоты реализуют все базовые операции над динамическими множествами за время O(h). Таким образом, операции выполняются тем быстрее, чем меньше высота дерева. Однако в худшем случае производительность бинарного дерева поиска оказывается ничуть не лучше, чем производительность связанного списка. Красно-черные деревья являются одними из множества «сбалансированных» схем деревьев поиска, гарантирующих время выполнения операций над динамической множеством O (lg n) даже в худшем случае.
Красно-черное дерево (англ. Red-Black-Tree, RB-Tree) — это одно из самобалансирующихся двоичных деревьев поиска, гарантирующих логарифмический рост высоты дерева от числа узлов и быстро выполняющее основные операции дерева поиска: добавление, удаление и поиск узла. Сбалансированность достигается за счет введения дополнительного атрибута узла дерева — «цвета». Этот атрибут может принимать одно из двух возможных значений — «черный» или «красный».
Изобретателем красно-черного дерева считают немца Рудольфа Байера. Название «красно-черное дерево» структура данных получила в статье Л. Гимпаса и Р. Седжвика (1978). В журнале были доступны две краски (красная и черная) и дополнительный бит, «прикреплявшийся» к каждому из узлов, обозначался цветом.
| Красно-черное дерево | ||
|---|---|---|
| Тип | дерево поиска | |
| Изобретено в | 1972 году | |
| Изобретено | Рудольф Байер | |
| Временная сложность в О-символике |
||
| В среднем | В худшем случае | |
| Расход памяти | O(n) | O(n) |
| Поиск | O(log n) | O(log n) |
| Вставка | O(log n) | O(log n) |
| Удаление | O(log n) | O(log n) |

Пример красно-черного дерева
Красно-черное дерево — двоичное дерево поиска, в котором каждый узел имеет атрибутцвет, принимающий значения красный или черный. В дополнение к обычным требованиям, налагаемым на двоичные деревья поиска, к красно-черным деревьям применяются следующие требования:
Эти ограничения реализуют критическое свойство красно-черных деревьев: путь от корня до самого дальнего листа не более чем в два раза длиннее пути от корня до ближайшего листа (если дальний лист расположен на 3-м уровне). Результатом является то, что дерево примерно сбалансировано. Так как такие операции как вставка, удаление и поиск значений требуют в худшем случае времени, пропорционального длине дерева, эта теоретическая верхняя граница высоты позволяет красно-черным деревьям быть более эффективными в худшем случае, чем обычные двоичные деревья поиска.
Чтобы понять, почему это гарантируется, достаточно рассмотреть эффект свойств 4 и 5 вместе. Пусть для красно-черного дерева T число черных узлов в свойстве 5 равно B. Тогда кратчайший возможный путь от корня дерева T до любого листового узла содержит B черных узлов. Более длинный возможный путь может быть построен путем включения красных узлов. Однако, свойство 4 не позволяет вставить несколько красных узлов подряд. Поэтому самый длинный возможный путь состоит из 2B узлов, попеременно красных и черных. Любой максимальный путь имеет одинаковое число черных узлов (по свойству 5), следовательно, не существует пути, более чем вдвое длинного, чем любой другой путь.
Во многих реализациях структуры дерева возможно, чтобы узел имел только одного потомка и листовой узел содержал данные. В этих предположениях реализовать красно-черное дерево возможно, но изменятся несколько свойств и алгоритм усложнится. По этой причине данная статья использует «фиктивные листовые узлы», которые не содержат данных и просто служат для указания, где дерево заканчивается. Эти узлы часто опускаются при графическом изображении, в результате дерево выглядит противоречиво с вышеизложенными принципами, но на самом деле противоречия нет. Следствием этого является то, что все внутренние (не являющиеся листовыми) узлы имеют два потомка, хотя один из них может быть нулевым листом. Свойство 5 гарантирует, что красный узел обязан иметь в качестве потомков либо два черных нулевых листа, либо два черных внутренних узла. Для черного узла с одним потомком нулевым листовым узлом и другим потомком, не являющимся таковым, свойства 3, 4 и 5 гарантируют, что последний должен быть красным узлом с двумя черными нулевыми листьями в качестве потомков.
Иногда красно-черное дерево трактуют как бинарное дерево поиска, у которого вместо узлов в красный и черный цвета раскрашены ребра, но это не имеет какого-либо значения. Цвет узла в терминах данной статьи соответствует цвету ребра, соединяющего узел со своим предком, за исключением того, что корневой узел всегда черный (свойство 2), в то время как соответствующее ребро не существует.
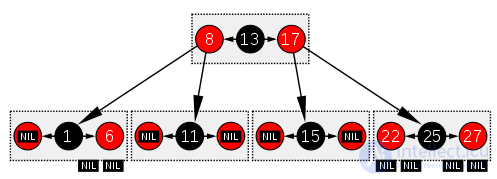
То же самое красно-черное дерево, что и в примере выше, представленное как B-дерево.
Красно-черное дерево схоже по структуре с B-деревом с параметром 2, в котором каждый узел может содержать от 1 до 3 значений и, соответственно, от 2 до 4 указателей на потомков. В таком В-дереве каждый узел будет содержать только одно значение, соответствующее значению черного узла красно-черного дерева с необязательным значениями до и/или после него в том же узле, оба из которых соответствуют эквивалентным красным узлам красно-черного дерева.
Один из способов увидеть эту эквивалентность — «поднять» красные узлы в графическом представлении красно-черного дерева так, чтобы они оказались на одном уровне по горизонтали со своими предками черными узлами, образуя страницу. В В-дереве, или в модифицированном графическом представлении красно-черного дерева, у всех листовых узлов глубина одинаковая.
Этот тип В-дерева является более общим, чем красно-черное дерево, хотя, как видно, из одного такого В-дерева с параметом 2 могут быть получены несколько красно-черных деревьев. Если страница В-дерева содержит только одно значение, данный узел черный и имеет двух потомков. Если страница содержит три значения, то центральный узел является черным, а каждый его сосед — красным. Однако, если страница содержит два значения, любой узел может стать черным в красно-черном дереве (и тогда второй будет красным).
Красно-черные деревья являются одними из наиболее активно используемых на практике самобалансирующихся деревьев поиска. В частности, контейнеры set и map в большинстве реализаций библиотеки STL языка C++ , класс TreeMap языка Java , так же, как и многие другие реализации ассоциативного массива в различных библиотеках, основаны на красно-черных деревьях.
Популярность красно-черных деревьев связана с тем, что на них часто достигается подходящий баланс между степенью сбалансированности и сложностью поддержки сбалансированности. В частности, при сравнении с идеально сбалансированными деревьями часто обнаруживается, что последние имеют слишком жесткое условие сбалансированности и при выполнении операций удаления из дерева много времени тратится на поддержание необходимой сбалансированности.
Операции чтения для красно-черного дерева ничем не отличаются от иных для бинарного дерева поиска, потому что любое красно-черное дерево является особым случаем обычного бинарного дерева поиска. Однако непосредственный результат вставки или удаления может привести к нарушению свойств красно-черных деревьев. Восстановление свойств требует небольшого (O(log n) или O(1)) числа операций смены цветов (которая на практике очень быстрая) и не более чем трех поворотов дерева (для вставки — не более двух). Хотя вставка и удаление сложны, их трудоемкость остается O(log n).
Вставка начинается с добавления узла, точно так же, как и в обычном бинарном дереве поиска, и окрашивания его в красный цвет. Но если в бинарном дереве поиска мы всегда добавляем лист, в красно-черном дереве листья не содержат данных, поэтому мы добавляем красный внутренний узел с двумя черными потомками на место черного листа.
Что происходит дальше зависит от цвета близлежащих узлов. Термин дядя будем использовать для обозначения брата родительского узла, как и в фамильном дереве. Заметим, что:
Примечание: Буквой N будем обозначать текущий узел (окрашенный красным). Сначала это новый узел, который вставляется, но эта процедура может рекурсивно применена к другим узлам (смотрите случай 3). P будем обозначать предка N, через G обозначим дедушку N, а U будем обозначать дядю N. Отметим, что в некоторых случаях роли узлов могут меняться, но, в любом случае, каждое обозначение будет представлять тот же узел, что и в начале. Любой цвет, изображенный на рисунке, либо предполагается в данном случае, либо получается из других соображений.
Каждый случай рассматривается с примерами кода на языке C. Дядя и дедушка текущего узла могут быть найдены с помощью функций:
struct node *
grandparent(struct node *n)
{
if ((n != NULL) && (n->parent != NULL))
return n->parent->parent;
else
return NULL;
}
struct node *
uncle(struct node *n)
{
struct node *g = grandparent(n);
if (g == NULL)
return NULL; // No grandparent means no uncle
if (n->parent == g->left)
return g->right;
else
return g->left;
}
Случай 1: Текущий узел N в корне дерева. В этом случае, он перекрашивается в черный цвет, чтобы оставить верным Свойство 2 (Корень — черный). Так как это действие добавляет один черный узел в каждый путь, Свойство 5 (Все пути от любого данного узла до листовых узлов содержат одинаковое число черных узлов) не нарушается.
void
insert_case1(struct node *n)
{
if (n->parent == NULL)
n->color = BLACK;
else
insert_case2(n);
}
Случай 2: Предок P текущего узла черный, то есть Свойство 4 (Оба потомка каждого красного узла — черные) не нарушается. В этом случае дерево действительно. Свойство 5 (Все пути от любого данного узла до листовых узлов содержат одинаковое число черных узлов) не нарушается, потому что текущий узел N имеет двух черных листовых потомков, но так как N является красным, пути до каждого из этих потомков содержит такое же число черных узлов, что и путь до черного листа, который был заменен текущим узлом, так что свойство остается верным.
void
insert_case2(struct node *n)
{
if (n->parent->color == BLACK)
return; /* Tree is still valid */
else
insert_case3(n);
}
Примечание: В следующих случаях предполагается, что у N есть дедушка G, так как его родитель P является красным, а если бы он был корнем, то был бы окрашен в черный цвет. Об этом говорит сайт https://intellect.icu . Таким образом, N также имеет дядю U, хотя он может быть листовым узлом в случаях 4 и 5.
|
Случай 3: Если и родитель P и дядя U — красные, то они оба могут быть перекрашены в черный и дедушка G станет красным (для сохранения свойства 5 (Все пути от любого данного узла до листовых узлов содержат одинаковое число черных узлов)). Теперь у текущего красного узла N черный родитель. Так как любой путь через родителя или дядю должен проходить через дедушку, число черных узлов в этих путях не изменится. Однако, дедушка G теперь может нарушить свойства 2 (Корень — черный) или 4 (Оба потомка каждого красного узла — черные) (свойство 4 может быть нарушено, так как родитель G может быть красным). Чтобы это исправить, вся процедура рекурсивно выполняется на Gиз случая 1. |
void
insert_case3(struct node *n)
{
struct node *u = uncle(n), *g;
if ((u != NULL) && (u->color == RED) && (n->parent->color == RED)) {
n->parent->color = BLACK;
u->color = BLACK;
g = grandparent(n);
g->color = RED;
insert_case1(g);
} else {
insert_case4(n);
}
}
Примечание: В оставшихся случаях предполагается, что родитель P является левым потомком своего предка. Если это не так, необходимо поменять лево и право. Примеры кода позаботятся об этом.
|
Случай 4: Родитель P является красным, но дядя U — черный. Также, текущий узел N — правый потомок P, а P в свою очередь — левый потомок своего предка G. В этом случае может быть произведен поворот дерева, который меняет роли текущего узла N и его предка P. Тогда, для бывшего родительского узла P в обновленно структуре используем случай 5, потому что Свойство 4 (Оба потомка любого красного узла — черные) все еще нарушено. Вращение приводит к тому, что некоторые пути (в поддереве, обозначенном «1» на схеме) проходят через узел N, чего не было до этого. Это также приводит к тому, что некоторые пути (в поддереве, обозначенном «3») не проходят через узел P. Однако, оба эти узла являются красными, так что Свойство 5 (Все пути от любого данного узла до листовых узлов содержат одинаковое число черных узлов) не нарушается при вращении. Однако Свойство 4 все еще нарушается, но теперь задача сводится к Случаю 5. |
void
insert_case4(struct node *n)
{
struct node *g = grandparent(n);
if ((n == n->parent->right) && (n->parent == g->left)) {
rotate_left(n->parent);
/*
* rotate_left может быть выполнен следующим образом, учитывая что уже есть *g = grandparent(n)
*
* struct node *saved_p=g->left, *saved_left_n=n->left;
* g->left=n;
* n->left=saved_p;
* saved_p->right=saved_left_n;
*
*/
n = n->left;
} else if ((n == n->parent->left) && (n->parent == g->right)) {
rotate_right(n->parent);
/*
* rotate_right может быть выполнен следующим образом, учитывая что уже есть *g = grandparent(n)
*
* struct node *saved_p=g->right, *saved_right_n=n->right;
* g->right=n;
* n->right=saved_p;
* saved_p->left=saved_right_n;
*
*/
n = n->right;
}
insert_case5(n);
}
|
Случай 5: Родитель P является красным, но дядя U — черный, текущий узел N — левый потомок P и P — левый потомок G. В этом случае выполняется поворот дерева на G. В результате получается дерево, в котором бывший родитель P теперь является родителем и текущего узла N и бывшего дедушки G. Известно, что G — черный, так как его бывший потомок P не мог бы в противном случае быть красным (без нарушения Свойства 4). Тогда цвета P и Gменяются и в результате дерево удовлетворяет Свойству 4 (Оба потомка любого красного узла — черные). Свойство 5 (Все пути от любого данного узла до листовых узлов содержат одинаковое число черных узлов) также остается верным, так как все пути, которые проходят через любой из этих трех узлов, ранее проходили через G, поэтому теперь они все проходят через P. В каждом случае, из этих трех узлов только один окрашен в черный. |
void
insert_case5(struct node *n)
{
struct node *g = grandparent(n);
n->parent->color = BLACK;
g->color = RED;
if ((n == n->parent->left) && (n->parent == g->left)) {
rotate_right(g);
} else { /* (n == n->parent->right) && (n->parent == g->right) */
rotate_left(g);
}
}
При удалении узла с двумя не листовыми потомками в обычном двоичном дереве поиска мы ищем либо наибольший элемент в его левом поддереве, либо наименьший элемент в его правом поддереве и перемещаем его значение в удаляемый узел. Затем мы удаляем узел, из которого копировали значение. Копирование значения из одного узла в другой не нарушает свойств красно-черного дерева, так как структура дерева и цвета узлов не изменяются. Стоит заметить, что новый удаляемый узел не может иметь сразу два дочерних нелистовых узла, так как в противном случае он не будет являться наибольшим/наименьшим элементом. Таким образом, получается, что случай удаления узла, имеющего два нелистовых потомка, сводится к случаю удаления узла, содержащего как минимум один дочерний листовой узел. Поэтому дальнейшее описание будет исходить из предположения существования у удаляемого узла не более одного нелистового потомка.
Будем использовать обозначение M для удаляемого узла; через C обозначим потомка M, который также будем называть просто «его потомок». Если M имеет не листового потомка, возьмем его за C. В противном случае за C возьмем любой из листовых потомков.
Если M является красным узлом, заменим его своим потомком C, который по определению должен быть черным. (Это может произойти только тогда, когда M имеет двух листовых потомков, потому что если красный узел M имеет черного не листового потомка с одной стороны, а с другой стороны — листового, то число черных узлов на обеих сторонах будет различным, таким образом дерево станет недействительным красно-черным деревом из-за нарушения Свойства 5.) Все пути через удаляемый узел просто будут содержать на один красный узел меньше, предок и потомок удаляемого узла должны быть черными, так что Свойство 3 («Все листья — черные») и Свойство 4 («Оба потомка красного узла — черные») все еще сохраняется.
Другим простым является случай, когда M — черный и C — красный. Простое удаление черного узла нарушит Свойство 4 («Оба потомка красного узла — черные») и Свойство 5 («Всякий простой путь от данного узла до любого листового узла, содержит одинаковое число черных узлов»), но если мы перекрасим С в черный, оба эти свойства сохранятся.
Сложным является случай, когда и M и C — черные. (Это может произойти только тогда, когда удаляется черный узел, который имеет два листовых потомка, потому что если черный узел M имеет черного не листового потомка с одной стороны, а с другой — листового, то число черных узлов на обеих сторонах будет различным и дерево станет недействительным красно-черным деревом из-за нарушения Свойства 5.) Мы начнем с замены узла M своим потомком C. Будем называть этот потомок (в своем новом положении) N, а его «брата» (другого потомка его нового предка) — S. (До этого S был «братом» M.) На рисунках ниже мы также будем использовать обозначение P для нового предка N (старого предка M), SL для левого потомка S и SR для правого потомка S (S не может быть листовым узлом, так как если N по нашему предположению является черным, то поддерево P, которое содержит N, черной высоты два и поэтому другое поддерево P, которое содержит S должно быть также черной высоты два, что не может быть в случае, когда S — лист).
Примечание: В некоторых случаях мы меняем роли и обозначения узлов, но в каждом случае любое обозначение продолжает означать тот же узел, что и в начале случая. Любые цвета, изображенные на рисунке либо предполагаются случаем, либо получается из других предположений. Белый означает неизвестный цвет (либо красный, либо черный).
Будем искать «брата», используя эту функцию:
struct node *
sibling(struct node *n)
{
if (n == n->parent->left)
return n->parent->right;
else
return n->parent->left;
}
Примечание: Для того, чтобы дерево оставалось верно определенным, нам нужно, чтобы каждый лист оставался листом после всех преобразований (чтобы у него не было потомков). Если удаляемый нами узел — не листовой потомок N, легко видеть, что свойство выполняется. С другой стороны, если N — лист, то, как можно увидеть из рисунков или кода, свойство также выполняется.
Мы можем выполнить действия, описанные выше, используя следующий код, где функция replace_node ставит child на место узла n в дереве. Для удобства, код в этом разделе предполагает, что нулевые листья представлены реальными объектами узла, а не NULL (код вставки должен работать с таким же представлением).
void
delete_one_child(struct node *n)
{
/*
* Условие: n имеет не более одного ненулевого потомка.
*/
struct node *child = is_leaf(n->right) ? n->left : n->right;
replace_node(n, child);
if (n->color == BLACK) {
if (child->color == RED)
child->color = BLACK;
else
delete_case1(child);
}
free(n);
}
Примечание: Если N является нулевым листом и мы не хотим представлять нулевые листы как реальные объекты, мы можем изменить алгоритм сначала вызывая delete_case1() на его отца (узел, который мы удалили, n в коде выше) и удаляя его после этого. Мы можем сделать это потому, что отец черный, и поэтому ведет себя так же как нулевой лист (и иногда называется 'phantom' лист). Мы можем безопасно удалить его так как n останется листом после всех операций, как показано выше.
Если оба N и его текущий отец черные, тогда удаление отца приведет к тому, что пути, которые проходят через N будут иметь на один черный узел меньше, чем пути, которые не проходят через него. Так как это нарушает свойство 5 (все пути из любого узла к его листовым узлам содержат одинаковое количество черных узлов), дерево должно быть перебалансировано. Есть несколько случаев для рассмотрения:
Случай 1: N — новый корень. В этом случае, все сделано. Мы удалили один черный узел из каждого пути и новый корень является черным узлом, так что свойства сохранены.
void
delete_case1(struct node *n)
{
if (n->parent != NULL)
delete_case2(n);
}
Примечание: В случаях 2, 5, и 6 мы предполагаем, что N является левым потомком своего предка P. Если он — правый потомок, left и right нужно поменять местами во всех трех случаях. Опять-таки, примеры кода принимают это во внимание.
|
Случай 2: S — красный. В этом случае мы меняем цвета P и S, и затем делаем вращение влево вокруг P, ставя Sдедушкой N. Нужно заметить, что P должен быть черным, если он имеет красного потомка. Хотя все пути по прежнему содержат одинаковое количество черных узлов, сейчас N имеет черного брата и красного отца. Таким образом, мы можем перейти к шагу 4, 5 или 6. (Его новый брат является черным потому, что он был потомком красного S.) Далее через Sбудет обозначен новый брат N. |
void delete_case2(struct node *n)
{
struct node *s = sibling(n);
if (s->color == RED) {
n->parent->color = RED;
s->color = BLACK;
if (n == n->parent->left)
rotate_left(n->parent);
else
rotate_right(n->parent);
}
delete_case3(n);
}
|
Случай 3: P, S, и дети S' — черные. В этом случае мы просто перекрашиваем S в красный. В результате все пути, проходящие через S, но не проходящие через N, имеют на один черный узел меньше. Так как удаления отца Nприводит к тому, что все пути, проходящие через N, содержат на один черный узел меньше, то такие действия выравнивают баланс. Тем не менее, все проходящие через P пути теперь содержать на один черный узел меньше, чем пути, которые через P не проходят, поэтому свойство 5 (все пути из любой вершины к ее листовым узлам содержат одинаковое количество черных узлов) все еще нарушено. Чтобы это исправить, мы применяем процедуру перебалансировки к P, начиная со случая 1. |
void delete_case3(struct node *n)
{
struct node *s = sibling(n);
if ((n->parent->color == BLACK) &&
(s->color == BLACK) &&
(s->left->color == BLACK) &&
(s->right->color == BLACK)) {
s->color = RED;
delete_case1(n->parent);
} else
delete_case4(n);
}
|
Случай 4: S и его дети — черные, но P — красный. В этом случае мы просто меняем цвета S и P. Это не влияет на количество черных узлов на путях, проходящих через S, но добавит один к числу черных узлов на путях, проходящих через N, восстанавливая тем самым влиянние удаленного черного узла. |
void delete_case4(struct node *n)
{
struct node *s = sibling(n);
if ((n->parent->color == RED) &&
(s->color == BLACK) &&
(s->left->color == BLACK) &&
(s->right->color == BLACK)) {
s->color = RED;
n->parent->color = BLACK;
} else
delete_case5(n);
}
|
Случай 5: S — черный, левый потомок S — красный, правый потомок S — черный, и N является левым потомков своего отца. В этом случае мы вращаем дерево вправо вокруг S. Таким образом левый потомок S становится его отцом и новым братом N. После этого мы меняем цвета у S и его нового отца. Все пути по прежнему содержат одинаковое количество черных узлов, но теперь у N есть черный брат с красным правым потомком, и мы переходим к случаю 6. Ни N, ни его отец не влияют на эту трансформацию. (Для случая 6 мы обозначим через S нового брата N.) |
void delete_case5(struct node *n)
{
struct node *s = sibling(n);
if (s->color == BLACK) { /* this if statement is trivial,
due to case 2 (even though case 2 changed the sibling to a sibling's child,
the sibling's child can't be red, since no red parent can have a red child). */
/* the following statements just force the red to be on the left of the left of the parent,
or right of the right, so case six will rotate correctly. */
if ((n == n->parent->left) &&
(s->right->color == BLACK) &&
(s->left->color == RED)) { /* this last test is trivial too due to cases 2-4. */
s->color = RED;
s->left->color = BLACK;
rotate_right(s);
} else if ((n == n->parent->right) &&
(s->left->color == BLACK) &&
(s->right->color == RED)) {/* this last test is trivial too due to cases 2-4. */
s->color = RED;
s->right->color = BLACK;
rotate_left(s);
}
}
delete_case6(n);
}
|
Случай 6: S — черный, правый потомок S — красный, и N является левым потомком своего отца P. В этом случае мы вращаем дерево влево вокруг P, после чего S становится отцом P и своего правого потомка. Далее мы изменяем цвета уP и S, и делаем правого потомка S черным. Поддерево по прежнему имеет тот же цвет корня, поэтому свойства 4 (Оба потомка каждого красного узла — черные) и 5 (все пути из любой вершины к ее листовым узлам содержат одинаковое количество черных узлов) не нарушаются. Тем не менее, у N теперь появился дополнительный черный предок: либо Pстал черным, или он был черным и S был добавлен в качестве черного дедушки. Таким образом, проходящие через Nпути проходят через один ополнительный черный узел. Между тем, если путь не проходит через N, то есть 2 возможных варианта:
В любом случае, число черных узлов на этих путях не изменится. Поэтому, мы восстановили свойства 4 (Оба потомка каждого красного узла — черные) и 5 (все пути из любой вершины к ее листовым узлам содержат одинаковое количество черных узлов). Белый узел на диаграмме может быть как красным так и черным, но должен указывать на тот же цвет как в начале, так и в конце трансформации. |
void delete_case6(struct node *n)
{
struct node *s = sibling(n);
s->color = n->parent->color;
n->parent->color = BLACK;
if (n == n->parent->left) {
s->right->color = BLACK;
rotate_left(n->parent);
} else {
s->left->color = BLACK;
rotate_right(n->parent);
}
}
Все рекурсивные вызовы функции хвостовые и преобразуются в циклы, так что алгоритм требует памяти O(1). В алгоритме выше, все случаи связаны по очереди, кроме случая 3, где может произойти возврат к случаю 1, который применяется к предку узла: это единственный случай когда последовательная реализация будет эффективным циклом (после одного вращения в случае 3).
Так же, хвостовая рекурсия никогда не происходит на дочерних узлах, поэтому цикл хвостовой рекурсии может двигаться только от дочерних узлов к их последовательным родителям. Произойдет не более, чем O(log n) циклических возвратов к случаю 1 (где n — общее количество узлов в дереве до удаления). Если в случае 2 произойдет вращение (единственно возможное в цикле случаев 1-3), тогда отец узла N становится красным после вращения и мы выходим из цикла. Таким образом будет произведено не более одного вращения в течение этого цикла. После выхода из цикла произойдет не более двух дополнительных поворотов. А в целом произойдет не более трех поворотов дерева.
Пускай высота дерева h, минимальное количество вершин N. Тогда:
 . Поскольку
. Поскольку  ,
,  , N(h) растет как последовательность Фибоначчи, следовательно
, N(h) растет как последовательность Фибоначчи, следовательно 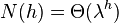 , где
, где 

Следовательно, при том же количестве листьев красно-черное дерево может быть выше АВЛ-дерева, но не более чем в  раз.
раз.
Поскольку красно-черное дерево, в худшем случае, выше, поиск в нем медленнее, но проигрыш по времени не превышает 39 %.
Удаление из красно-черного дерева требует до 3 поворотов, в АВЛ-дереве оно может потребовать числа поворотов до глубины дерева (до корня). Поэтому удаление из красно-черного дерева быстрее, чем из АВЛ-дерева.
АВЛ-дерево в каждом узле хранит разницу высот (целое число от −1 до +1, для кодирования нужно 2бита). Красно-черное дерево в каждом узле хранит цвет (1 бит). Таким образом, красно-черное дерево может быть экономичнее. (Правда если учитывать, что в современных вычислительных системах память выделяется кратно байтам, то деревья абсолютно одинаковы)
Однако, на практике в обоих типах деревьев используются целые числа, так как работа с битами требует дополнительных процессорных вычислений (одной команды ассемблера and %al 0x10000000). Но тем не менее есть реализации красно-черного дерева, которые хранят значение цвета в бите. Пример — Boost Multiindex. Цель хранения цвета в бите — уменьшение потребления памяти красно-черным деревом (Ordered indices node compression). Бит цвета в такой реализации хранится не в отдельной переменной, а в одном из указателей узла дерева (этот прием опасен выходом за границу доступной памяти).
 .
.Обозначения:
 — высота поддерева с корнем в
— высота поддерева с корнем в 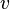
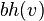 — число черных узлов (не считая
— число черных узлов (не считая 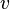 , если он черный) от
, если он черный) от 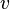 до любого листа в поддереве (называемое черной высотой)
до любого листа в поддереве (называемое черной высотой)Лемма: Поддерево с корнем в узле 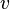 имеет не менее
имеет не менее 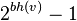 внутренних узлов.
внутренних узлов.
Доказательство леммы (индукцией по высоте):
Основание индукции:  .
.
Если поддерево имеет нулевую высоту, то 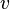 должен быть null, поэтому
должен быть null, поэтому  .
.
Итак:

Индукционный шаг: пусть узел 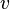 такой, что
такой, что 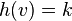 и поддерево имеет не менее
и поддерево имеет не менее 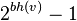 внутренних узлов.
внутренних узлов.
Покажем, что тогда  , для которого
, для которого 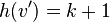 , имеет не менее
, имеет не менее  внутренних узлов.
внутренних узлов.
Так как  имеет
имеет  , это внутренний узел. Как таковой он имеет два потомка, оба из которых имеют черную высоту
, это внутренний узел. Как таковой он имеет два потомка, оба из которых имеют черную высоту 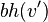 , либо
, либо  (зависит от того, является
(зависит от того, является  красным, или черным).
красным, или черным).
По индукционному предположению каждый потомок имеет не менее  внутренних узлов, поэтому
внутренних узлов, поэтому  имеет не менее
имеет не менее
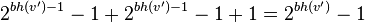
внутренних узлов.
Используя эту лемму, мы можем показать, что дерево имеет логарифмическую высоту. Так как по крайней мере половина узлов в любом пути от корня до листа — черные (свойство 4 красно-черного дерева), черная высота корня не менее  . По лемме имеем:
. По лемме имеем:

Поэтому высота корня  .
.
Надеюсь, эта статья про красно-черное, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое красно-черное, дерево поиска и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Структуры данных
Комментарии
Оставить комментарий
Структуры данных
Термины: Структуры данных