Лекция
Привет, сегодня поговорим про двоичное дерево поиска определение свойства операции, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое двоичное дерево поиска определение свойства операции , настоятельно рекомендую прочитать все из категории Структуры данных.
Двоичное дерево поиска (англ. binary search tree, BST) — это двоичное дерево, для которого выполняются следующие дополнительные условия (свойства дерева поиска):
Очевидно, данные в каждом узле должны обладать ключами, на которых определена операция сравнения меньше.
Как правило, информация, представляющая каждый узел, является записью, а не единственным полем данных. Однако, это касается реализации, а не природы двоичного дерева поиска.
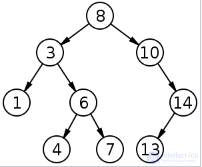
Пример двоичного дерева поиска
Содержание
Определение и свойства Двоичного дерева поиска, операции
1 Основные операции в двоичном дереве поиска
1.1 Поиск элемента (FIND)
1.2 Добавление элемента (INSERT)
1.3 Удаление узла (REMOVE)
1.4 Обход дерева (TRAVERSE)
1.5 Разбиение дерева по ключу
1.6 Объединение двух деревьев в одно
2 Балансировка дерева
3 Задачи о бинарном дереве поиска
| Двоичное дерево поиска | ||
|---|---|---|
| Тип | Дерево | |
| Временная сложность в О-символике |
||
| В среднем | В худшем случае | |
| Расход памяти | O(n) | O(n) |
| Поиск | O(log n) | O(n) |
| Вставка | O(log n) | O(n) |
| Удаление | O(log n) | O(n) |
Для целей реализации двоичное дерево поиска можно определить так:
Двоичное дерево поиска не следует путать с двоичной кучей, построенной по другим правилам.
Основным преимуществом двоичного дерева поиска перед другими структурами данных является возможная высокая эффективность реализации основанных на нем алгоритмов поиска и сортировки.
Двоичное дерево поиска применяется для построения более абстрактных структур, таких как множества, мультимножества, ассоциативные массивы.
Базовый интерфейс двоичного дерева поиска состоит из трех операций:
Этот абстрактный интерфейс является общим случаем, например, таких интерфейсов, взятых из прикладных задач:
По сути, двоичное дерево поиска — это структура данных, способная хранить таблицу пар (key, value) и поддерживающая три операции: FIND, INSERT, REMOVE.
Кроме того, интерфейс двоичного дерева включает еще три дополнительных операции обхода узлов дерева: INFIX_TRAVERSE, PREFIX_TRAVERSE и POSTFIX_TRAVERSE. Первая из них позволяет обойти узлы дерева в порядке неубывания ключей.
Дано: дерево Т и ключ K.
Задача: проверить, есть ли узел с ключом K в дереве Т, и если да, то вернуть ссылку на этот узел.
Алгоритм:
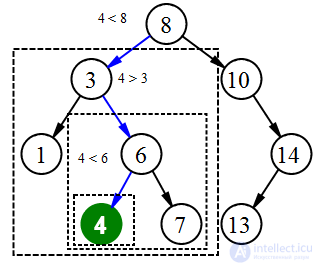
Поиск элемента 4
Для поиска элемента в бинарном дереве поиска можно воспользоваться следующей функцией, которая принимает в качестве параметров корень дерева и искомый ключ. Для каждого узла функция сравнивает значение его ключа с искомым ключом. Если ключи одинаковы, то функция возвращает текущий узел, в противном случае функция вызывается рекурсивно для левого или правого поддерева. Узлы, которые посещает функция образуют нисходящий путь от корня, так что время ее работы O(h)O(h), где hh — высота дерева.
Node search(x : Node, k : T):
if x == null or k == x.key
return x
if k < x.key
return search(x.left, k)
else
return search(x.right, k)
Чтобы найти минимальный элемент в бинарном дереве поиска, необходимо просто следовать указателям leftleft от корня дерева, пока не встретится значение nullnull. Если у вершины есть левое поддерево, то по свойству бинарного дерева поиска в нем хранятся все элементы с меньшим ключом. Если его нет, значит эта вершина и есть минимальная. Аналогично ищется и максимальный элемент. Для этого нужно следовать правым указателям.
Node minimum(x : Node):
if x.left == null
return x
return minimum(x.left)
Node maximum(x : Node):
if x.right == null
return x
return maximum(x.right)
Данные функции принимают корень поддерева, и возвращают минимальный (максимальный) элемент в поддереве. Обе процедуры выполняются за время O(h)O(h).
Реализация с использованием информации о родителе
Если у узла есть правое поддерево, то следующий за ним элемент будет минимальным элементом в этом поддереве. Если у него нет правого поддерева, то нужно следовать вверх, пока не встретим узел, который является левым дочерним узлом своего родителя. Поиск предыдущего выполнятся аналогично. Если у узла есть левое поддерево, то следующий за ним элемент будет максимальным элементом в этом поддереве. Если у него нет левого поддерева, то нужно следовать вверх, пока не встретим узел, который является правым дочерним узлом своего родителя.
Node next(x : Node):
if x.right != null
return minimum(x.right)
y = x.parent
while y != null and x == y.right
x = y
y = y.parent
return y
Node prev(x : Node):
if x.left != null
return maximum(x.left)
y = x.parent
while y != null and x == y.left
x = y
y = y.parent
return y
Обе операции выполняются за время O(h)O(h).
Реализация без использования информации о родителе
Рассмотрим поиск следующего элемента для некоторого ключа xx. Об этом говорит сайт https://intellect.icu . Поиск будем начинать с корня дерева, храня текущий узел currentcurrent и узел successorsuccessor, последний посещенный узел, ключ которого больше xx.
Спускаемся вниз по дереву, как в алгоритме поиска узла. Рассмотрим ключ текущего узла currentcurrent. Если current.key⩽xcurrent.key⩽x, значит следующий за xx узел находится в правом поддереве (в левом поддереве все ключи меньше current.keycurrent.key). Если же x<current.keyxx<next(x)⩽current.keyxcurrentcurrent может быть следующим для ключа xx, либо следующий узел содержится в левом поддереве currentcurrent. Перейдем к нужному поддереву и повторим те же самые действия.
Аналогично реализуется операция поиска предыдущего элемента.
Node next(x : T):
Node current = root, successor = null // root — корень дерева
while current != null
if current.key > x
successor = current
current = current.left
else
current = current.right
return successor
Дано: дерево Т и пара (K,V).
Задача: вставить пару (K, V) в дерево Т (при совпадении K, заменить V).
Алгоритм:
Второй пример
Операция вставки работает аналогично поиску элемента, только при обнаружении у элемента отсутствия ребенка нужно подвесить на него вставляемый элемент.
Реализация с использованием информации о родителе
func insert(x : Node, z : Node): // x — корень поддерева, z — вставляемый элемент
while x != null
if z.key > x.key
if x.right != null
x = x.right
else
z.parent = x
x.right = z
break
else if z.key < x.key
if x.left != null
x = x.left
else
z.parent = x
x.left = z
break
Реализация без использования информации о родителе
Node insert(x : Node, z : T): // x — корень поддерева, z — вставляемый ключ
if x == null
return Node(z) // подвесим Node с key = z
else if z < x.key
x.left = insert(x.left, z)
else if z > x.key
x.right = insert(x.right, z)
return x
Время работы алгоритма для обеих реализаций — O(h)O(h).
Дано: дерево Т с корнем n и ключом K.
Задача: удалить из дерева Т узел с ключом K (если такой есть).
Алгоритм:
Нерекурсивная реализация удаления узла из двоичного дерева поиска
Для удаления узла из бинарного дерева поиска нужно рассмотреть три возможные ситуации. Если у узла нет дочерних узлов, то у его родителя нужно просто заменить указатель на nullnull. Если у узла есть только один дочерний узел, то нужно создать новую связь между родителем удаляемого узла и его дочерним узлом. Наконец, если у узла два дочерних узла, то нужно найти следующий за ним элемент (у этого элемента не будет левого потомка), его правого потомка подвесить на место найденного элемента, а удаляемый узел заменить найденным узлом. Таким образом, свойство бинарного дерева поиска не будет нарушено. Данная реализация удаления не увеличивает высоту дерева. Время работы алгоритма — O(h)O(h).
| Случай | Иллюстрация |
|---|---|
| Удаление листа | 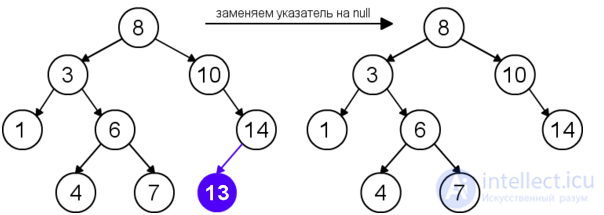 |
| Удаление узла с одним дочерним узлом | 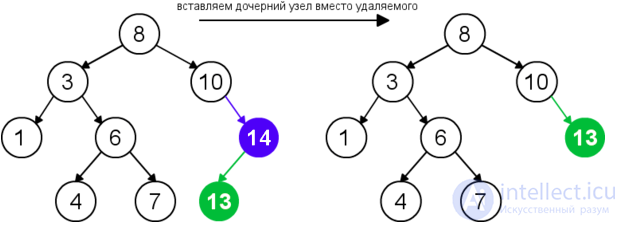 |
| Удаление узла с двумя дочерними узлами | 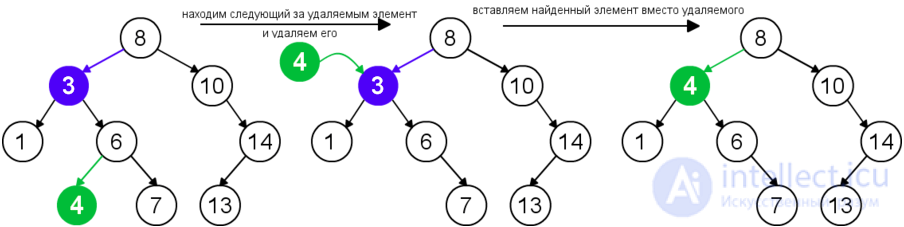 |
func delete(t : Node, v : Node): // tt — дерево, vv — удаляемый элемент
p = v.parent // предок удаляемого элемента
if v.left == null and v.right == null // первый случай: удаляемый элемент - лист
if p.left == v
p.left = null
if p.right == v
p.right = null
else if v.left == null or v.right == null // второй случай: удаляемый элемент имеет одного потомка
if v.left == null
if p.left == v
p.left = v.right
else
p.right = v.right
v.right.parent = p
else
if p.left == v
p.left = v.left
else
p.right = v.left
v.left.parent = p
else // третий случай: удаляемый элемент имеет двух потомков
successor = next(v, t)
v.key = successor.key
if successor.parent.left == successor
successor.parent.left = successor.right
if successor.right != null
successor.right.parent = successor.parent
else
successor.parent.right = successor.left
if successor.left != null
successor.right.parent = successor.parent
Рекурсивная реализация удаления узла из двоичного дерева поиска
При рекурсивном удалении узла из бинарного дерева нужно рассмотреть три случая: удаляемый элемент находится в левом поддереве текущего поддерева, удаляемый элемент находится в правом поддереве или удаляемый элемент находится в корне. В двух первых случаях нужно рекурсивно удалить элемент из нужного поддерева. Если удаляемый элемент находится в корне текущего поддерева и имеет два дочерних узла, то нужно заменить его минимальным элементом из правого поддерева и рекурсивно удалить этот минимальный элемент из правого поддерева. Иначе, если удаляемый элемент имеет один дочерний узел, нужно заменить его потомком. Время работы алгоритма — O(h)O(h). Рекурсивная функция, возвращающая дерево с удаленным элементом zz:
Node delete(root : Node, z : T): // корень поддерева, удаляемый ключ
if root == null
return root
if z < root.key
root.left = delete(root.left, z)
else if z > root.key
root.right = delete(root.right, z)
else if root.left != null and root.right != null
root.key = minimum(root.right).key
root.right = delete(root.right, root.key)
else
if root.left != null
root = root.left
else
root = root.right
return root
Есть три операции обхода узлов дерева, отличающиеся порядком обхода узлов.
Первая операция — INFIX_TRAVERSE — позволяет обойти все узлы дерева в порядке возрастания ключей и применить к каждому узлу заданную пользователемфункцию обратного вызова f, операндом которой является адрес узла. Эта функция обычно работает только с парой (K,V), хранящейся в узле. Операция INFIX_TRAVERSE может быть реализована рекурсивным образом: сначала она запускает себя для левого поддерева, потом запускает данную функцию для корня, потом запускает себя для правого поддерева.
В других источниках эти функции именуются inorder, preorder, postorder соответственно
INFIX_TRAVERSE
Дано: дерево Т и функция f
Задача: применить f ко всем узлам дерева Т в порядке возрастания ключей
Алгоритм:
В простейшем случае, функция f может выводить значение пары (K,V). При использовании операции INFIX_TRAVERSE будут выведены все пары в порядке возрастания ключей. Если же использовать PREFIX_TRAVERSE, то пары будут выведены в порядке, соответствующим описанию дерева, приведенного в начале статьи.
Для представления бинарного дерева поиска в памяти будем использовать следующую структуру:
struct Node: T key // ключ узла Node left // указатель на левого потомка Node right // указатель на правого потомка Node parent // указатель на предка
Есть три операции обхода узлов дерева, отличающиеся порядком обхода узлов:
func inorderTraversal(x : Node):
if x != null
inorderTraversal(x.left)
print x.key
inorderTraversal(x.right)
При выполнении данного обхода вершины будут выведены в следующем порядке: 1 3 4 6 7 8 10 13 14.
func preorderTraversal(x : Node)
if x != null
print x.key
preorderTraversal(x.left)
preorderTraversal(x.right)
При выполнении данного обхода вершины будут выведены в следующем порядке: 8 3 1 6 4 7 10 14 13.
func postorderTraversal(x : Node)
if x != null
postorderTraversal(x.left)
postorderTraversal(x.right)
print x.key
При выполнении данного обхода вершины будут выведены в следующем порядке: 1 4 7 6 3 13 14 10 8.
Данные алгоритмы выполняют обход за время O(n)O(n), поскольку процедура вызывается ровно два раза для каждого узла дерева.
Операция «разбиение дерева по ключу» позволяет разбить одно дерево поиска на два: с ключами <K0 и ≥K0.
Обратная операция: есть два дерева поиска, у одного ключи <K0, у другого ≥K0. Объединить их в одно дерево.
У нас есть два дерева: T1 (меньшее) и T2 (большее). Сначала нужно решить, откуда взять корень: из T1 или T2. Стандартного метода нет, возможные варианты:
алг ОбъединениеДеревьев(T1, T2) если T1 пустое, вернуть T2 если T2 пустое, вернуть T1 если решили сделать корнем T1, то T = ОбъединениеДеревьев(T1.правое, T2) T1.правое = T вернуть T1 иначе T = ОбъединениеДеревьев(T1, T2.левое) T2.левое = T вернуть T2
Всегда желательно, чтобы все пути в дереве от корня до листьев имели примерно одинаковую длину, то есть чтобы глубина и левого, и правого поддеревьев была примерно одинакова в любом узле. В противном случае теряется производительность.
В вырожденном случае может оказаться, что все левое дерево пусто на каждом уровне, есть только правые деревья, и в таком случае дерево вырождается в список (идущий вправо). Поиск (а значит, и удаление и добавление) в таком дереве по скорости равен поиску в списке и намного медленнее поиска в сбалансированном дереве.
Для балансировки дерева применяется операция «поворот дерева». Поворот налево выглядит так:

Поворот направо выглядит так же, достаточно заменить в вышеприведенном примере все Left на Right и обратно.
Достаточно очевидно, что поворот не нарушает упорядоченность дерева, и оказывает предсказуемое (+1 или −1) влияние на глубины всех затронутых поддеревьев.
Для принятия решения о том, какие именно повороты нужно совершать после добавления или удаления, используются такие алгоритмы, как «красно-черное дерево» иАВЛ.
Оба они требуют дополнительной информации в узлах — 1 бит у красно-черного или знаковое число у АВЛ.
Красно-черное дерево требует <= 2 поворотов после добавления и <= 3 после удаления, но при этом худший дисбаланс может оказаться до 2 раз (самый длинный путь в 2 раза длиннее самого короткого).
АВЛ-дерево требует <= 2 поворотов после добавления и до глубины дерева после удаления, но при этом идеально сбалансировано (дисбаланс не более, чем на 1).
Проверка того, что заданное дерево является деревом поиска
Задача:
Определить, является ли заданное двоичное дерево деревом поиска.
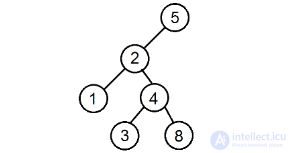
Пример дерева, для которого недостаточно проверки лишь его соседних вершин
Задачи на поиск максимального BST в заданном двоичном дереве
Задача:
Найти в данном дереве такую вершину, что она будет корнем поддерева поиска с наибольшим количеством вершин.
Восстановление дерева по результату обхода preorderTraversa
Задача:
Восстановить дерево по последовательности, выведенной после выполнения процедуры preorderTraversal.
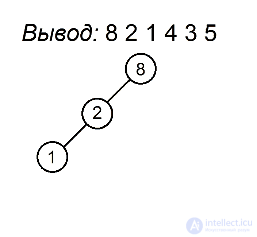
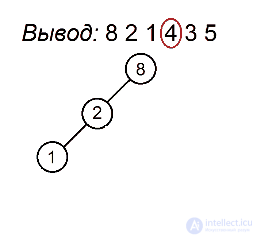
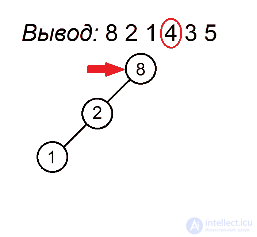
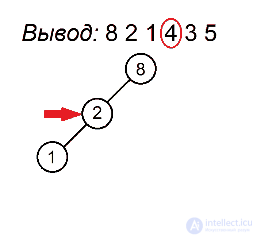
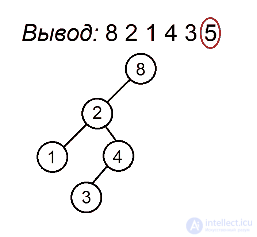
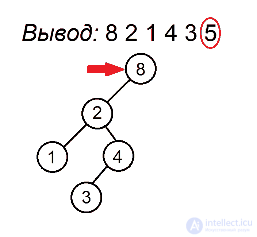
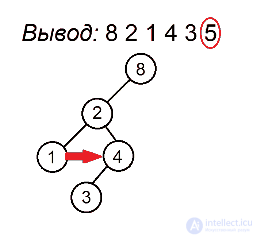
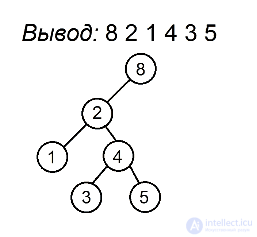
Как мы помним, процедура preorderTraversal выводит значения в узлах поддерева следующим образом: сначала идет до упора влево, затем на каком-то моменте делает шаг вправо и снова движется влево. Это продолжается до тех пор, пока не будут выведены все вершины. Полученная последовательность позволит нам однозначно определить расположение всех узлов поддерева. Первая вершина всегда будет в корне. Затем, пока не будут использованы все значения, будем последовательно подвешивать левых сыновей к последней добавленной вершине, пока не найдем номер, нарушающий убывающую последовательность, а для каждого такого номера будем искать вершину без правого потомка, хранящую наибольшее значение, не превосходящее того, которое хотим поставить, и подвешиваем к ней элемент с таким номером в качестве правого сына. Когда мы, желая найти такую вершину, встречаем какую-нибудь другую, уже имеющую правого сына, проходим по ветке вправо. Мы имеем на это право, так как если такая вершина стоит, то процедура обхода в ней уже побывала и поворачивала вправо, поэтому спускаться в другую сторону смысла не имеет. Вершину с максимальным ключом, с которой будем начинать поиск, будем запоминать. Она будет обновляться каждый раз, когда появится новый максимум.
Процедура восстановления дерева работает за O(n).
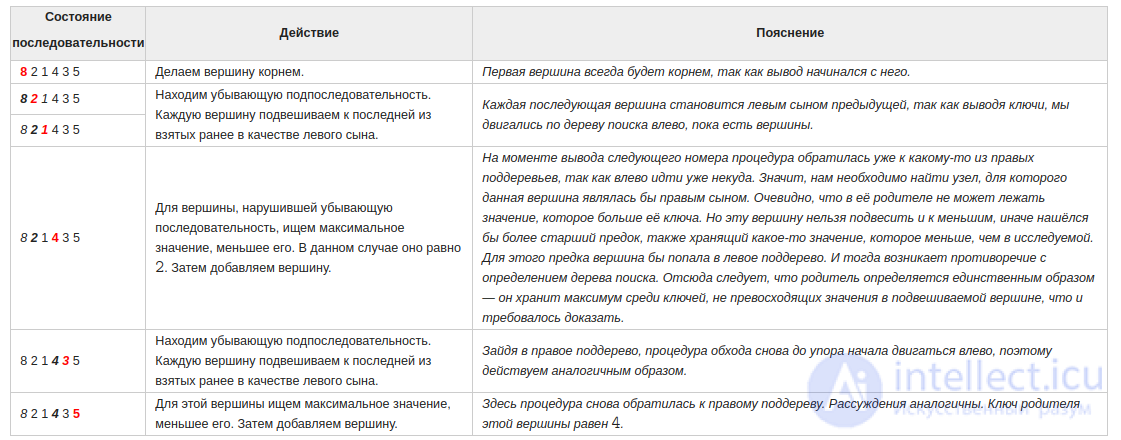
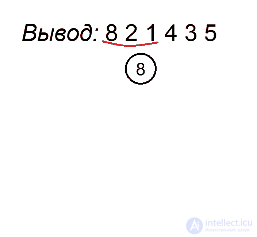
Разберем алгоритм на примере последовательности 8 2 1 4 3 5
Будем выделять красным цветом вершины, рассматриваемые на каждом шаге, черным жирным — их родителей, курсивом — убывающие подпоследовательности (в случаях, когда мы их рассматриваем) или претендентов на добавление к ним правого ребенка (когда рассматривается вершина, нарушающая убывающую последовательность).






Сбалансированные деревья :
На этом все! Теперь вы знаете все про двоичное дерево поиска определение свойства операции, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое двоичное дерево поиска определение свойства операции и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Структуры данных
Комментарии
Оставить комментарий
Структуры данных
Термины: Структуры данных