Лекция
Привет, Вы узнаете о том , что такое дерево, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое дерево, обход дерева, двоичные деревья, бинарные деревья, двоичное дерево, бинарное дерево , настоятельно рекомендую прочитать все из категории Структуры данных.
дерево — является одна из наиболее широко распространенных структур данных в информатике, эмулирующая древовидную структуру в виде набора связанных узлов. Является связным графом, не содержащим циклы. Большинство источников также добавляют условие на то, что ребра графа не должны быть ориентированными. В дополнение к этим трем ограничениям, в некоторых источниках указывается, что ребра графа не должны быть взвешенными.
Дерево — называется структура, в которой у каждого узла может быть ноль или более подузлов — «детей».
Как известно, программы состоят из двух частей — алгоритмов и структур данных. В хорошей программе эти составляющие эффективно дополняют друг друга. Выбор и реализация структуры данных насколько же важны, как и процедуры для обработки данных. Способ организации и доступа к информации обычно определяется природой программируемой задачи. Таким образом, для программиста важно иметь в своем распоряжении приемы, подходящие для различных ситуаций.
Степень привязки типа данных к своему машинному представлению находится в обратной зависимости от его абстракции. Другими словами, чем более абстрактными становятся типы данных, тем больше концептуальное представление о способе хранения этих данных отличается от реального, фактического способа их хранения в памяти компьютера Простые типы, например, char или int, тесно связаны со своим машинным представлением. Например, машинное представление целочисленного значения хорошо аппроксимирует соответствующую концепцию программирования. По мере своего усложнения типы данных становятся концептуально менее похожими на свои машинные эквиваленты. Так, действительные числа с плавающей точкой более абстрактны, чем целые числа. Фактическое представление типа float в машине весьма приблизительно соответствует представлению среднего программиста о действительном числе. Еще более абстрактной является структура, принадлежащая к составным типам данных.
На следующем уровне абстракции сугубо физические аспекты данных отходят на второй план вследствие введения механизма доступа(data engine) к данным, то есть механизма сохранения и получения информации. По существу, физические данные связываются с механизмом доступа, который управляет работой с данными из программы. Именно механизмам доступа к данным и посвящена эта глава.
Существует четыре механизма доступа:
Каждый из этих методов дает возможность решать задачи определенного класса. Эти методы по существу являются механизмами, выполняющими определенные операции сохранения и получения передаваемой им информации на основе получаемых ими запросов. Они все сохраняют и получают элемент, здесь под элементом подразумевается информационная единица. В этой главе показано, как создавать такие механизмы доступа на языке С. При этом проиллюстрированы некоторые распространенные приемы программирования в С, включая динамическое выделение памяти и использование указателей.

Другие названия: магазин, стековая память, магазинная память, память магазинного типа, запоминающее устройство магазинного типа, стековое запоминающее устройство.
Другие названия: цепной список, список с использованием указателей, список со ссылками, список на указателях.
Другие названия: дерево двоичного поиска.

Дерево считается ориентированным, если в корень не заходит ни одно ребро.
Узел является экземпляром одного из двух типов элементов графа, соответствующим объекту некоторой фиксированной природы. Узел может содержать значение, состояние или представление отдельной информационной структуры или самого дерева. Каждый узел дерева имеет ноль или более узлов-потомков, которые располагаются ниже по дереву (по соглашению, деревья "растут" вниз, а не вверх, как это происходит с настоящими деревьями). Узел, имеющий потомка, называется узлом-родителем относительно своего потомка (или узлом-предшественником, или старшим). Каждый узел имеет не больше одного предка. Высота узла — это максимальная длина нисходящего пути от этого узла к самому нижнему узлу (краевому узлу), называемому листом. Высота корневого узла равна высоте всего дерева. Глубина вложенности узла равна длине пути до корневого узла.
Узел, не имеющий предков (самый верхний), называется корневым узлом. Это узел, на котором начинается выполнение большинства операций над деревом (хотя некоторые алгоритмы начинают выполнение с «листов» и выполняются, пока не достигнут корня). Все прочие узлы могут быть достигнуты путем перехода от корневого узла по ребрам (или ссылкам) (согласно формальному определению, каждый подобный путь должен быть уникальным). В диаграммах он обычно изображается на самой вершине. В некоторых деревьях, например, кучах, корневой узел обладает особыми свойствами. Каждый узел дерева можно рассматривать как корневой узел поддерева, «растущего» из этого узла.
Поддерево — часть древообразной структуры данных, которая может быть представлена в виде отдельного дерева. Любой узел дерева T вместе со всеми его узлами-потомками является поддеревом дерева T. Для любого узла поддерева либо должен быть путь в корневой узел этого поддерева, либо сам узел должен являться корневым. То есть поддерево связано с корневым узлом целым деревом, а отношения поддерева со всеми прочими узлами определяются через понятие соответствующее поддерево (по аналогии с термином «соответствующее подмножество»).
Как уже говорилось выше, двоичные (бинарные) деревья – это деревья со степенью не более двух.
По степени вершин двоичные деревья бывают:
строгие – вершины дерева имеют степень ноль (у листьев) или два (у узлов);
нестрогие – вершины дерева имеют степень ноль (у листьев), один или два (у узлов).
В общем случае на k-м уровне двоичного дерева может быть до 2k-1 вершин.
Двоичное дерево, содержащее только полностью заполненные уровни (то есть 2k-1 вершин на каждом k-м уровне), называется полным.

Рисунок 16. Двоичные деревья
Существует два основных типа деревьев. В рекурсивном дереве или неупорядоченном дереве имеет значение лишь структура самого дерева без учета порядка потомков для каждого узла. Дерево, в котором задан порядок (например, каждому ребру, ведущему к потомку, присвоены различные натуральные числа) называется деревом с именованными ребрами или упорядоченным деревом со структурой данных, заданной перед именованием и называемой структурой данных упорядоченного дерева.
Упорядоченные деревья являются наиболее распространенными среди древовидных структур. Двоичное дерево поиска — одно из разновидностей упорядоченного дерева.
Существует множество различных способов представления деревьев. Наиболее общий способ представления изображает узлы как записи, расположенные в динамически выделяемой памяти с указателями на своих потомков, предков (или и тех и других), или как элементы массива, связанные между собой отношениями, определенными их позициями в массиве (например, двоичная куча).
В теории графов дерево — связный ациклический граф. Корневое дерево — это граф с вершиной, выделенной в качестве корневой. В этом случае любые две вершины, связанные ребром, наследуют отношения «родитель-потомок». Несвязный граф, состоящий исключительно из деревьев, называется лесом.
Пошаговый перебор элементов дерева по связям между узлами-предками и узлами-потомками называется обходом дерева. Зачастую операция может быть выполнена переходом указателя по отдельным узлам. Обход, при котором каждый узел-предок просматривается прежде его потомков, называется предупорядоченным обходом или обходом в прямом порядке (pre-order walk), а когда просматриваются сначала потомки, а потом предки, то обход называется поступорядоченным обходом или обходом в обратном порядке (post-order walk). Об этом говорит сайт https://intellect.icu . Существует также симметричный обход, при котором посещается сначала левое поддерево, затем узел, затем — правое поддерево, и обход в ширину, при котором узлы посещаются уровень за уровнем (N-й уровень дерева — множество узлов с высотой N). Каждый уровень обходится слева направо.
Напоследок мы рассмотрим структуру данных, которая называется двоичное дерево (binary tree). Несмотря на то, что бывает много различных типов деревьев, двоичные деревья играют особую роль, так как в отсортированном состоянии позволяют очень быстро выполнять вставку, удаление и поиск. Каждый элемент двоичного дерева состоит из информационной части и указателей на левый и правый элементы. На рис. 22.8 показано небольшое двоичное дерево.
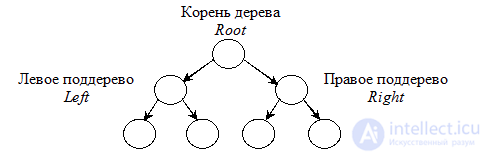
Рис. 22.8. Пример двоичного дерева, высота которого равна 2
Такая структура данных организуется следующим образом (N – NULL):
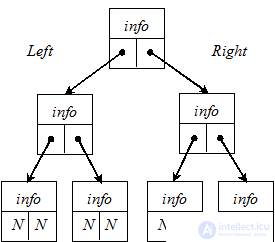
При обсуждении деревьев применяется специальная терминология. Программисты не являются специалистами в области филологии, и поэтому терминология, применяемая в теории графов (а ведь деревья представляют собой частный случай графов!), является классическим примером неправильного употребления слов. Первый элемент дерева называется корнем (root). Каждый элемент данных называется вершиной дерева (node), а любой фрагмент дерева называется поддеревом (subtree). Вершина, к которой не присоединены поддеревья, называетсязаключительным узлом (terminal node) или листом (leaf). Высота (height) дерева равняется максимальному количеству уровней от корня до листа. При работе с деревьями можно допустить, что в памяти они существуют в том же виде, что и на бумаге. Но помните, что дерево — всего лишь способ логической организации данных в памяти, а память линейна.
В некотором смысле двоичное дерево является особым видом связанного списка. Элементы можно вставлять, удалять и извлекать в любом порядке. Кроме того, операция извлечения не является разрушающей. Несмотря на то, что деревья легко представить в воображении, в теории программирования с ними связан ряд сложных задач. В данном разделе деревья затрагиваются лишь поверхностно.
Большинство функций, работающих с деревьями, рекурсивны, поскольку дерево по своей сути является рекурсивной структурой данных. Другими словами, каждое поддерево, в свою очередь, является деревом. Поэтому разрабатываемые здесь функции будут рекурсивными. Существуют и не рекурсивные версии этих функций, но их код понять намного сложнее.
Способ упорядочивания дерева зависит от того, как к нему впоследствии будет осуществляться доступ. Процесс поочередного доступа к каждой вершине дерева называется обходом (вершин) дерева (tree traversal). Рассмотрим следующее дерево:
d
↙ ↘
b f
↙ ↘ ↙ ↘
a c e g
Существует три порядка обхода дерева: обход симметричным способом, или симметричный обход (inorder), обход в прямом порядке, прямой обход, упорядоченный обход, обход сверху, или обход в ширину (preorder) и обход в обратном порядке, обход в глубину, обратный обход, обход снизу (postorder). При симметричном обходе обрабатывается сначала левое поддерево, затем корень, а затем правое поддерево. При прямом обходе обрабатывается сначала корень, затем левое поддерево, а потом правое. При обходе снизу сначала обрабатывается левое поддерево, затем правое и, наконец корень. Последовательность доступа при каждом методе обхода показана ниже:
Симметричный обход a b c d e f g Прямой обход d b a c f e g Обход снизу a c b e g f d
Несмотря на то, что дерево не должно быть обязательно упорядоченным, в большинстве задач используются именно такие деревья. Конечно, структура упорядоченного дерева зависит от способа его обхода. В оставшейся части данной главы предполагается симметричный обход. Поэтому упорядоченным двоичным деревом будет считаться такое дерево, в котором левое поддерево содержит вершины, меньшие или равные корню, а правое содержит вершины, большие корня.
Приведенная ниже функция stree() создает упорядоченное двоичное дерево:
struct tree {
char info;
struct tree *left;
struct tree *right;
};
struct tree *stree(
struct tree *root,
struct tree *r,
char info)
{
if(!r) {
r = (struct tree *) malloc(sizeof(struct tree));
if(!r) {
printf("Не хватает памяти\n");
exit(0);
}
r->left = NULL;
r->right = NULL;
r->info = info;
if(!root) return r; /* первый вход */
if(info < root->info) root->left = r;
else root->right = r;
return r;
}
if(info < r->info)
stree(r,r->left,info);
else
stree(r,r->right,info);
return root;
}
Приведенный выше алгоритм просто следует по ссылкам дерева, переходя к левой или правой ветви очередной вершины на основании содержимого поля info до достижения места вставки нового элемента. Чтобы использовать эту функцию, необходимо иметь глобальную переменную-указатель на корень дерева. Этот указатель изначально должен иметь значение нуль (NULL). При первом вызове функция stree()возвращает указатель на корень дерева, который нужно присвоить глобальной переменной. При последующих вызовах функция продолжает возвращать указатель на корень. Допустим, что глобальная переменная, содержащая корень дерева, называется rt. Тогда функция stree()вызывается следующим образом:
/* вызов функции street() */ rt = street(rt, rt, info);
Функция stree() использует рекурсивный алгоритм, как и большинство процедур работы с деревьями. Точно такая же функция, основанная на итеративных методах, была бы в несколько раз длиннее. Функцию stree() необходимо вызывать со следующими параметрами (слева направо): указатель на корень всего дерева, указатель на корень следующего поддерева, в котором осуществляется поиск, и сохраняемые данные. При первом вызове оба первых параметрах указывают на корень всего дерева. Для простоты в вершинах дерева хранятся одиночные символы. Тем не менее, вместо них можно использовать любой тип данных.
Чтобы обойти созданное функцией stree() дерево в симметричном порядке и распечатать поле info в каждой вершине, можно применить приведенную ниже функцию inorder():
void inorder(struct tree *root)
{
if(!root) return;
inorder(root->left);
if(root->info) printf("%c ", root->info);
inorder(root->right);
}
Данная рекурсивная функция завершает работу тогда, когда находит заключительный узел (нулевой указатель).
В следующем листинге показаны функции, выполняющие обход дерева в ширину и в глубину.
void preorder(struct tree *root)
{
if(!root) return;
if(root->info) printf("%c ", root->info);
preorder(root->left);
preorder(root->right);
}
void postorder(struct tree *root)
{
if(!root) return;
postorder(root->left);
postorder(root->right);
if(root->info) printf("%c ", root->info);
}
Теперь давайте рассмотрим короткую, но интересную программу, которая строит упорядоченное двоичное дерево, а затем, обходя его симметричным образом, отображает его на экране боком. Для отображения дерева требуется лишь слегка модифицировать функцию inorder(). Поскольку на экране дерево распечатывается боком, для корректного отображения правое поддерево необходимо печатать прежде левого. (Технически это противоположность симметричного обхода.) Новая функция называется printtree(), а ее код показан ниже:
void print_tree(struct tree *r, int l)
{
int i;
if(r == NULL) return;
print_tree(r->right, l+1);
for(i=0; iinfo);
print_tree(r->left, l+1);
}
Далее следует текст всей программы печати дерева. Попробуйте вводить различные деревья, чтобы увидеть, как они строятся.
/* Эта программа выводит на экран двоичное дерево. */
#include
#include
struct tree {
char info;
struct tree *left;
struct tree *right;
};
struct tree *root; /* начальная вершина дерева */
struct tree *stree(struct tree *root,
struct tree *r, char info);
void print_tree(struct tree *root, int l);
int main(void)
{
char s[80];
root = NULL; /* инициализация корня дерева */
do {
printf("Введите букву: ");
gets(s);
root = stree(root, root, *s);
} while(*s);
print_tree(root, 0);
return 0;
}
struct tree *stree(
struct tree *root,
struct tree *r,
char info)
{
if(!r) {
r = (struct tree *) malloc(sizeof(struct tree));
if(!r) {
printf("Не хватает памяти\n");
exit(0);
}
r->left = NULL;
r->right = NULL;
r->info = info;
if(!root) return r; /* первый вход */
if(info < root->info) root->left = r;
else root->right = r;
return r;
}
if(info < r->info)
stree(r, r->left, info);
else
stree(r, r->right, info);
return root;
}
void print_tree(struct tree *r, int l)
{
int i;
if(!r) return;
print_tree(r->right, l+1);
for(i=0; iinfo);
print_tree(r->left, l+1);
}
По существу, данная программа сортирует вводимую информацию. Метод сортировки является одной из разновидностей сортировки методом вставок, которая была рассмотрена в предыдущей главе. В среднем случае производительность может быть вполне хорошей.
Если вы запускали программу печати дерева, вы, вероятно, заметили, что некоторые деревья являются сбалансированными (balanced), т.е. каждое поддерево имеет примерно такую же высоту, как и остальные, а некоторые деревья очень далеки от этого состояния. Например, дерево a⇒b⇒c⇒d выглядит следующим образом:
В этом дереве нет левых поддеревьев. Такое дерево называется вырожденным, поскольку фактически оно выродилось в линейный список. В общем случае, если при построении дерева вводимые данные являются случайными, то получаемое дерево оказывается близким к сбалансированному. Если же информация предварительно отсортирована, создается вырожденное дерево. (Поэтому иногда при каждой вставке дерево корректируют так, чтобы оно было сбалансированным, но этот процесс довольно сложен и выходит за рамки данной главы.)
В двоичных деревьях легко реализовываются функции поиска. Приведенная ниже функция возвращает указатель на вершину дерева, в которой информация совпадает с ключом поиска, либо нуль (NULL), если такой вершины нет.
struct tree *search_tree(struct tree *root, char key)
{
if(!root) return root; /* пустое дерево */
while(root->info != key) {
if(keyinfo) root = root->left;
else root = root->right;
if(root == NULL) break;
}
return root;
}
К сожалению, удалить вершину дерева не так просто, как отыскать. Удаляемая вершина может быть либо корнем, либо левой, либо правой вершиной. Помимо того, к вершине могут быть присоединены поддеревья (количество присоединенных поддеревьев может равняться 0, 1 или 2). Процесс переустановки указателей подсказывает рекурсивный алгоритм, приведенный ниже:
struct tree *dtree(struct tree *root, char key)
{
struct tree *p,*p2;
if(!root) return root; /* вершина не найдена */
if(root->info == key) { /* удаление корня */
/* это означает пустое дерево */
if(root->left == root->right){
free(root);
return NULL;
}
/* или если одно из поддеревьев пустое */
else if(root->left == NULL) {
p = root->right;
free(root);
return p;
}
else if(root->right == NULL) {
p = root->left;
free(root);
return p;
}
/* или есть оба поддерева */
else {
p2 = root->right;
p = root->right;
while(p->left) p = p->left;
p->left = root->left;
free(root);
return p2;
}
}
if(root->info < key) root->right = dtree(root->right, key);
else root->left = dtree(root->left, key);
return root;
}
Необходимо также следить за правильным обновлением указателя на корень дерева, описанного вне данной функции, поскольку удаляемая вершина может быть корнем. Лучше всего с этой целью указателю на корень присваивать значение, возвращаемое функциейdtree():
root = dtree(root, key);
Двоичные деревья — исключительно мощное, гибкое и эффективное средство. Поскольку при поиске в сбалансированном дереве выполняется в худшем случае log2n сравнений, оно намного лучше, чем связанный список, в котором возможен лишь последовательный поиск.
Двоичное дерево можно реализовывать как статическую структуру данных в виде одномерного массива, а можно как динамическую структуру – в виде списка.
Списочное представление двоичных деревьев основано на элементах, соответствующих узлам дерева. Каждый элемент имеет поле данных и два поля указателей. Один указатель используется для связывания элемента с правым потомком, а другой – с левым. Листья имеют пустые указатели потомков. При таком способе представления дерева обязательно следует сохранять указатель на узел, являющийся корнем дерева.
type
PTree = ^TTree;
TTree = record
Data: TypeElement; {поле данных}
Left, Right: PTree; {указатели на левого и правого потомков}
end;
В виде массива проще всего представляется полное двоичное дерево, так как оно всегда имеет строго определенное число вершин на каждом уровне. Вершины можно пронумеровать слева направо последовательно по уровням и использовать эти номера в качестве индексов в одномерном массиве. Если число уровней дерева в процессе обработки не будет существенно изменяться, то такой способ представления полного двоичного дерева будет значительно более экономичным, чем любая списковая структура.
type
Tree: array[1..N] of TypeElement
Адрес любой вершины в массиве вычисляется как
адрес = 2k-1+i-1,
где k – номер уровня вершины, i – номер на уровне k в полном двоичном дереве. Адрес корня будет равен единице. Для любой вершины, имеющей индекс j в массиве, можно вычислить адреса левого и правого потомков
адрес_левого = 2*j
адрес_правого = 2*j+1
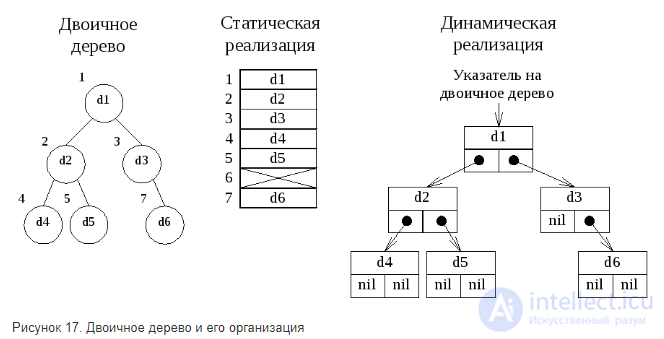
Рисунок 17. Двоичное дерево и его организация
Главным недостатком статического способа представления двоичного дерева является то, что массив имеет фиксированную длину. Размер массива выбирается исходя из максимально возможного количества уровней двоичного дерева, и чем менее полным является дерево, тем менее рационально используется память. Кроме того, недостатком являются большие накладные расходы при изменении структуры дерева (например, при обмене местами двух поддеревьев).
Ориентированные и упорядоченные ориентированные деревья интенсивно используются в программировании.
1. Выражения. Для представления выражений языков программирования, как правило, используются ориентированные упорядоченные деревья. Пример представления выражения а + b· с показан на рисунке слева.
2. Для представления блочной структуры программы и связанной с ней структуры областей определения идентификаторов часто используется ориентированное дерево (может быть, неупорядоченное, так как порядок определения переменных в блоке в большинстве языков программирования считается несущественным).
На рисунке в центре показана структура областей определения идентификаторов а, b, с,d,e, причем для отображения структуры дерева использована альтернативная техника.
3. Для представления иерархической структуры вложенности элементов данных и/или операторов управления часто используется техника отступов, показанная на рисунке справа.

4. Структура вложенности каталогов и файлов в современных операционных систе-мах является упорядоченным ориентированным деревом.
5. Различные "уравновешенные скобочные структуры" (например (a(b)(c(d)(e)))) являются ориентированными упорядоченными деревьями.
Это отражается даже в терминологии – "корневой каталог диска".
Замечание:Общепринятой практикой при изображении деревьев является соглашение о том, что корень находится наверху и все стрелки дуг ориентированы сверху вниз, поэтому стрелки можно не изображать. Таким образом, диаграммы свободных, ориентированных и упорядоченных деревьев оказываются графически неотличимыми, и требуется дополнительное указание, дерево какого класса изображено на диаграмме. В большинстве случаев это ясно из контекста.
Пример:На рис. 8.8 приведены три диаграммы деревьев, которые внешне выглядят различными. Обозначим дерево слева – (1), в центре – (2) и справа – (3). Как упорядоченные деревья, они все различны: (1) ^ (2), (2) ^ (3), (3) ^ (1). Как ориентированные деревья (1) = (2), но (2) ^ (3). Как свободные деревья, они все изоморфны: (1) = (2) = (3).
В практическом программировании для организации хранения данных и доступа к ним часто используется механизм, который называют ассоциативной памятью. При использовании ассоциативной памяти данные делятся на порции (записи), и с каждой записью ассоциируется ключ. Ключ – значение из некоторого вполне упорядоченного множества. Записи могут иметь произвольную природу и различные размеры. Доступ к данным осуществляется по ключу, который выбирают простым, компактным и удобным для работы.
Пример: Пример ассоциативной памяти. Банковский счет: ключ – номер счета, запись – финансовая информация.
Ассоциативная память должна поддерживать три основные операции:
1)Добавить (ключ, запись);
)Найти (запись по ключу);
3)Удалить (ключ).
Для представления ассоциативной памяти используют следующие структуры данных:
1)Неупорядоченный массив;
2)Упорядоченный массив;
3)Дерево сортировки ( бинарное дерево , каждый узел которого содержит ключ и обладает следующим свойством: значение ключа во всех узлах левого поддерева меньше, а во всех узлах правого поддерева больше, чем значение ключа в узле).
4)Таблица расстановки, или хэш-таблица.
Основная идея таблицы расстановки состоит в том, что подбирается специальная функция, которая называется хэш-функцией, переводящая значение ключа в адрес хранения записи. Адресом может быть индекс в массиве, номер кластера на диске и т.д. Таким образом, имея ключ, с помощью хэш-функции сразу определяется место хранения записи и открывается доступ к ней.
Эффективность ассоциативной памяти зависит от структуры используемых для ее представления данных. Дерево сортировки может расти неравномерно при реализации операций с ассоциативной памятью. Например, если при загрузке дерево исходных данных уже упорядочено, то полученное дерево будет право- или леволинейным и будет даже менее эффективно, чем неупорядоченный массив.
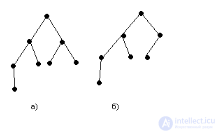
Наибольший эффект при поиске дают выровненные деревья. Ордерево – выровненное, если все узлы, степень которых меньше 2, располагаются на одном или двух последних уровнях.
Пример:На рисунке показаны диаграммы выровненного (а) и невыровненного (б) деревьев.
Распространенные древовидные структуры
Самобалансирующиеся двоичные деревья поиска
Прочие деревья
Исследование, описанное в статье про дерево, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое дерево, обход дерева, двоичные деревья, бинарные деревья, двоичное дерево, бинарное дерево и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Структуры данных
Комментарии
Оставить комментарий
Структуры данных
Термины: Структуры данных