Лекция
Привет, Вы узнаете о том , что такое задачи rmq, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое задачи rmq, задачи lca , настоятельно рекомендую прочитать все из категории Структуры данных.
Задача RMQ весьма часто встречается в спортивном и прикладном программировании.
Аббревиатура RMQ расшифровывается как Range Minimum (Maximum) Query – запрос минимума (максимума) на отрезке в массиве. Для определенности мы будем рассматривать операцию взятия минимума.
Пусть дан массив A[1..n]. Нам необходимо уметь отвечать на запрос вида «найти минимум на отрезке с i-ого элемента по j-ый».
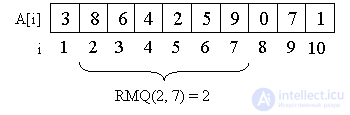
Рассмотрим в качестве примера массив A = {3, 8, 6, 4, 2, 5, 9, 0, 7, 1}.
Например, минимум на отрезке со второго элемента по седьмой равен двум, то есть RMQ(2, 7) = 2.
В голову приходит очевидное решение: ответ на каждый запрос будем находить, просто пробегаясь по всем элементам массива, лежащим на нужном нам отрезке. Такое решение, однако, не является самым эффективным. Ведь в худшем случае нам придется пробежаться по O(n) элементам, т.е. временная сложность этого алгоритма – O(n) на один запрос. Однако, задачу можно решить эффективнее.
Для начала уточним постановку задачи.
Что значит слово static в заголовке статьи? Задачу RMQ иногда ставят с возможностью изменения элементов массива. То есть к запросу взятия минимума добавляется возможность изменения элемента, или даже изменения элементов на отрезке (например, увеличения всех элементов на подотрезке на 3). Такой вариант задачи, называемый dynamic RMQ, я рассмотрю в последующих статьях.
Замечу здесь же, что задачу RMQ подразделяют на offline и online версии. В offline-варианте есть возможность сначала получить все запросы, проанализировать их каким-нибудь образом и только потом выдать на них ответ. В online-постановке запросы даются по очереди, т.е. следующий запрос поступает только после ответа на предыдущий. Заметим, что решив RMQ в online-постановке, мы сразу получаем решение и для offline RMQ, правда, может существовать более эффективное решение для offline RMQ, не применимое для online-постановки.
В этой статье мы будем рассматривать static online RMQ.
Для оценки эффективности алгоритма введем еще одну временнýю характеристику – время препроцессинга. В ней будем учитывать время на подготовку, т.е. предподсчет некоторой информации, необходимой для ответа на запросы.
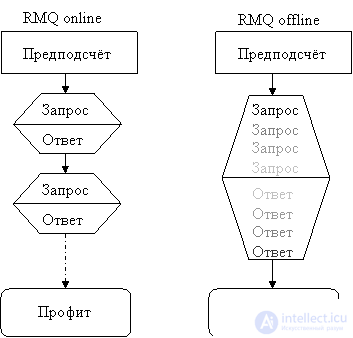
Казалось бы, зачем нам надо выделять препроцессинг отдельно? А вот зачем. Приведем еще одно решение задачи.
Перед тем как начать отвечать на запросы, возьмем и просто насчитаем ответ для каждого отрезка! Т.е. построим массив P[n][n] (в дальнейшем я буду пользоваться C-подобным синтаксисом, хотя массив A буду нумеровать с единицы для простоты реализации), где P[i][j] будет равняться минимуму на отрезке с i до j. Причем насчитаем этот массив хоть за O(n3) – самым тупым образом, пробегаясь по всем элементам для каждого отрезка. Зачем мы это делаем? Предположим, количество запросов q намного больше n3. Тогда общее время работы нашего алгоритма – O(n3) + q * O(1) = O(q), т.е. время на препроцессинг по большому счету и не повлияет на общее время работы алгоритма. Зато благодаря насчитанной информации мы научились отвечать на запрос за время O(1) вместо O(n). Ясно, что O(q) лучше O(qn).
С другой стороны, при q < n3 время препроцессинга будет играть свою роль, и в приведенном алгоритме оно – O(n3) – к сожалению, является слишком большим, даже несмотря на то, что его можно снизить (подумайте как) до O(n2).
Начиная с этого момента будем обозначать временные характеристики алгоритма как (P(n), Q(n)), где P(n) – время на предподсчет и Q(n) – время на ответ на один запрос.
Итак, мы имеем два алгоритма. Один работает за (O(1), O(n)), второй – за (O(n2), O(1)). Научимся решать задачу за (O(nlogn), O(1)), где logn – двоичный логарифм n.
Лирическое отступление. Заметим, что в качестве основания логарифма можно брать любое число, т.к. logan всегда отличается от logbn ровно в константное число раз. Константа, как мы помним из курса школьной алгебры равна logab.
Итак, мы дошли до следующего шага:
Sparse Table – это таблица ST[][] такая, что ST[k][i] есть минимум на полуинтервале [A[i], A[i+2k]). Иными словами, она содержит минимумы на всех отрезках, длина которых есть степень двойки.

Насчитаем массив ST[k][i] следующим образом. Понятно, что ST просто и есть наш массив A. Далее воспользуемся понятным свойством:
ST[k][i] = min(ST[k-1][i], ST[k-1][i + 2k — 1]). Благодаря нему мы можем сначала посчитать ST , потом ST и т. д.
Заметим, что в нашей таблице O(nlogn) элементов, потому что номера уровней должны быть не больше logn, т. к. при больших значениях k длина полуинтервала становится больше длины всего массива и хранить соответствующие значения бессмысленно. И на каждом уровне O(n) элементов.
Снова лирическое отступление: Легко заметить, что у нас остается много неиспользованных элементов массива. Не стоит ли по-другому хранить таблицу дабы не тратить память впустую? Оценим количество незадействованной памяти в нашей реализации. На i-ом ряду неиспользованных элементов – 2i – 1. Значит, всего неиспользованными остается Σ(2i – 1) = O(2logn) = O(n), т. е. в любом случае понадобится порядка O(nlogn) – O(n) = O(nlogn) места для хранения Sparse Table. Значит, можно не беспокоиться о неиспользуемых элементах.
А теперь главный вопрос: зачем мы все это считали? Заметим, что любой отрезок массива разбивается на два перекрывающихся подотрезка длиною в степень двойки.
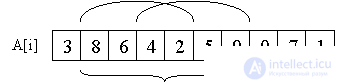
Получаем простую формулу для вычисления RMQ(i, j). Если k = log(j – i + 1), то RMQ(i, j) = min(ST(i, k), ST(j – 2k + 1, k)). Об этом говорит сайт https://intellect.icu . Тем самым, получаем алгоритм за (O(nlogn), O(1)). Ура!
…почти получаем. Как мы логарифм считать собрались за O(1)? Проще всего его тоже предподсчитать для всех значений, не превосходящих n. Понятно, что асимптотика препроцессинга от этого не изменится.
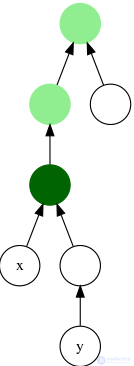
Нахождение за O (sqrt (N)) и O (log N) с препроцессингом O (N). Пусть дано дерево G. На вход поступают запросы вида (V1, V2), для каждого запроса требуется найти их наименьшего общего предка, т.е. вершину V, которая лежит на пути от корня до V1, на пути от корня до V2, и из всех таких вершин следует выбирать самую нижнюю. Иными словами, искомая вершина V - предок и V1, и V2, и среди всех таких общих предков выбирается нижний. Очевидно, что наименьший общий предок вершин V1 и V2 - это их общий предок, лежащий на кратчайшем пути из V1 в V2. В частности, например, если V1 является предком V2, то V1 является их наименьшим общим предком.
На английском эта задача называется задачей LCA - Least Common Ancestor.
Перед тем, как отвечать на запросы, выполним так называемый препроцессинг. Запустим обход в глубину из корня, который будет строить список посещения вершин Order (текущая вершина добавляется в список при входе в эту вершину, а также после каждого возвращения из ее сына), нетрудно заметить, что итоговый размер этого списка будет O (N). И построим массив First[1..N], в котором для каждой вершины будет указана позиция в массиве Order, в которой стоит эта вершина, т.е. Order[First[I]] = I для всех I. Также с помощью поиска в глубину найдем высоту каждой вершины (расстояние от корня до нее) - H[1..N].
Как теперь отвечать на запросы? Пусть имеется текущий запрос - пара вершин V1 и V2. Рассмотрим список Order между индексами First[V1] и First[V2]. Нетрудно заметить, что в этом диапазоне будет находиться и искомое LCA (V1, V2), а также множество других вершин. Однако LCA (V1, V2) будет отличаться от остальных вершин тем, что это будет вершина с наименьшей высотой.
Таким образом, чтобы ответить на запрос, нам нужно просто найти вершину с наименьшей высотой в массиве Order в диапазоне между First[V1] и First[V2]. Таким образом, задача LCA сводится к задаче RMQ ("минимум на отрезке"). А последняя задача решается с помощью структур данных (см. задача RMQ).
Если использовать sqrt-декомпозицию, то можно получить решение, отвечающее на запрос за O (sqrt (N)) и выполняющее препроцессинг за O (N).
Если использовать дерево отрезков, то можно получить решение, отвечающее на запрос за O (log (N)) и выполняющее препроцессинг за O (N).
Здесь будет приведена готовая реализация LCA с использованием дерева отрезков:
typedef vector < vector<int> > graph;
typedef vector<int>::const_iterator const_graph_iter;
vector<int> lca_h, lca_dfs_list, lca_first, lca_tree;
vector<char> lca_dfs_used;
void lca_dfs (const graph & g, int v, int h = 1)
{
lca_dfs_used[v] = true;
lca_h[v] = h;
lca_dfs_list.push_back (v);
for (const_graph_iter i = g[v].begin(); i != g[v].end(); ++i)
if (!lca_dfs_used[*i])
{
lca_dfs (g, *i, h+1);
lca_dfs_list.push_back (v);
}
}
void lca_build_tree (int i, int l, int r)
{
if (l == r)
lca_tree[i] = lca_dfs_list[l];
else
{
int m = (l + r) >> 1;
lca_build_tree (i+i, l, m);
lca_build_tree (i+i+1, m+1, r);
if (lca_h[lca_tree[i+i]] < lca_h[lca_tree[i+i+1]])
lca_tree[i] = lca_tree[i+i];
else
lca_tree[i] = lca_tree[i+i+1];
}
}
void lca_prepare (const graph & g, int root)
{
int n = (int) g.size();
lca_h.resize (n);
lca_dfs_list.reserve (n*2);
lca_dfs_used.assign (n, 0);
lca_dfs (g, root);
int m = (int) lca_dfs_list.size();
lca_tree.assign (lca_dfs_list.size() * 4 + 1, -1);
lca_build_tree (1, 0, m-1);
lca_first.assign (n, -1);
for (int i = 0; i < m; ++i)
{
int v = lca_dfs_list[i];
if (lca_first[v] == -1)
lca_first[v] = i;
}
}
int lca_tree_min (int i, int sl, int sr, int l, int r)
{
if (sl == l && sr == r)
return lca_tree[i];
int sm = (sl + sr) >> 1;
if (r <= sm)
return lca_tree_min (i+i, sl, sm, l, r);
if (l > sm)
return lca_tree_min (i+i+1, sm+1, sr, l, r);
int ans1 = lca_tree_min (i+i, sl, sm, l, sm);
int ans2 = lca_tree_min (i+i+1, sm+1, sr, sm+1, r);
return lca_h[ans1] < lca_h[ans2] ? ans1 : ans2;
}
int lca (int a, int b)
{
int left = lca_first[a],
right = lca_first[b];
if (left > right) swap (left, right);
return lca_tree_min (1, 0, (int)lca_dfs_list.size()-1, left, right);
}
int main()
{
graph g;
int root;
... чтение графа ...
lca_prepare (g, root);
for (;;)
{
int v1, v2; // поступил запрос
int v = lca (v1, v2); // ответ на запрос
}
}
Самый простой, наивный алгоритм для нахождения наименьшего общего предка — вычислить глубину вершин u и v и постепенно подниматься из каждой вершины вверх по дереву, пока не будет найдена общая вершина:
Процедура LCA(u, v):
h1 := depth(u) // depth(x) = глубина вершины x
h2 := depth(v)
while h1 ≠ h2:
if h1 > h2:
u := parent(u)
h1 := h1 - 1
else:
v := parent(v)
h2 := h2 - 1
while u ≠ v:
u := parent(u) // parent(x) = непосредственный предок вершины x
v := parent(v)
return u
Время работы этого алгоритма составляет O(h), где h — высота дерева. Кроме того, может понадобиться препроцессинг, требующий O(n) времени, для нахождения непосредственного предка для всех вершин дерева (но, как правило, эта структура на дереве уже имеется).
Однако, есть более быстрые алгоритмы:
Проблема вычисления низших общих предков классов в иерархии наследования возникает при реализации систем объектно-ориентированного программирования ( Aït-Kaci et al. 1989 ). Проблема LCA также находит применение в моделях сложных систем, используемых в распределенных вычислениях ( Bender et al. 2005 ).
| Задача: |
| Дан массив A[1..N]. Поступают запросы вида (i,j), на каждый запрос требуется найти минимум в массиве A, начиная с позиции i и заканчивая позицией j. |
Будем решать задачу RMQ, уже умея решать задачу LCA. Для хранения решения задачи о LCA будем использовать декартово дерево по неявному ключу. Тогда минимум на отрезке от i до j массива A будет равен наименьшему общему предку i-того и j-того элементов из декартова дерева, построенного на массиве A.
Декартово дерево по неявному ключу на массиве A[1..N] — это бинарное дерево, допускающее следующее рекурсивное построение:
Здесь и далее A[i] будет также использоваться для обозначения соответствующей вершины дерева.
Построим декартово дерево на массиве AA. Тогда RMQ(i,j) = LCA(A[i],A[j]).
Положим w=LCA(A[i],A[j]).
Заметим, что A[i] и A[j] не принадлежат одновременно либо правому, либо левому поддереву w, потому как тогда бы соответствующий сын находился на большей глубине, чем ww, и также являлся предком как A[i], так и A[j], что противоречит определению LCA. Из этого замечания следует, что w лежит между A[i] и A[j] и, следовательно, принадлежит отрезку A[i..j].
По построению мы также знаем, что:
Суммируя, получаем, что ww имеет минимальное значение на отрезке, покрывающем A[i..j], и принадлежит отрезку A[i..j], отсюда
RMQ(i,j)=w.
Существует алгоритм, который строит декартово дерево за O(n). Используя алгоритм построения LCA, получаем: препроцессинг для LCA — O(n) и ответ на запрос — O(1).
Нам нужно единожды построить декартово дерево за O(n), единожды провести препроцессинг за O(n) и отвечать на запросы за O(1).
В итоге получили RMQ с построением за O(n) и ответом на запрос за O(1).
Данная статья про задачи rmq подтверждают значимость применения современных методик для изучения данных проблем. Надеюсь, что теперь ты понял что такое задачи rmq, задачи lca и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Структуры данных
Комментарии
Оставить комментарий
Структуры данных
Термины: Структуры данных