Лекция
Привет, сегодня поговорим про бинарные деревья, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое бинарные деревья , настоятельно рекомендую прочитать все из категории Структуры данных.
Цель работы: исследовать и изучить процедуры, используемые при работе с бинарными (двоичными) деревьями.
Задача работы: овладеть навыками написания программ по исследованию бинарных деревьев .
Порядок работы :
Общие сведения о структуре данных – дерево.
Дерево - это нелинейная связанная структура данных, характеризуемая следующими признаками :
Каждый узел дерева может быть промежуточным (элементы 2,3,5,7) либо терминальным ("листом" дерева) (элементы 4,9,10,11,8,6). Характерной особенностью терминальных узлов является отсутствие ветвей.

Элемент Y, находящийся непосредственно ниже элемента X, называется непосредственным потомком X, если X находится на уровне i , то говорят, что Y лежит на уровне i+1.
Считается, что корень лежит на уровне 0.
Число непосредственных потомков элемента называется его степенью исхода, в зависимости от степени исхода узлов деревья классифицируют :
Особенно важную роль играют
бинарные деревья , далее мы будем рассматривать их более подробно.
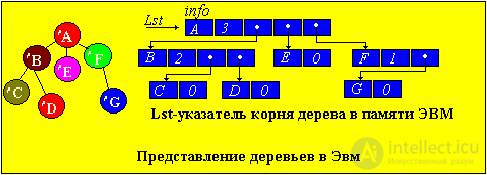
Представление деревьев в памяти ЭВМ
Деревья наиболее удобно представлять в памяти ЭВМ в виде связанных нелинейных списков. Элемент должен содержать INFO-поле, где содержится характеристика узла. Следующее поле определяет степень исхода узла и количество полей указателей равное степени исхода. Каждый указатель элемента ориентирует данный элемент-узел с его сыновьями. Узлы, в которые входят стрелки от исходного элемента, называются его сыновьями.
INFO-поле содержит два поля : поле записи (rec) и поле ключа (key). Ключ задается числом, по ключу определяют место элемента в дереве.
Сведение М-арного дерева к бинарному
1. В каждом узле дерева отсекают все ветви, кроме крайних левых, соответствующих старшим сыновьям;
2. Соединяют горизонтальными линиями сыновей одного родителя (узла);

Построение бинарных деревьев
Согласно представлению деревьев в памяти ЭВМ каждый элемент (узел бинарного дерева) будет записью, содержащей четыре поля. Значением этих полей будут соответственно ключ записи, ссылка на элемент влево-вниз, на элемент вправо-вниз и на текст записи.
При построении необходимо помнить, что левый сын имеет ключ меньше чем отец (родитель). Значение ключа правого сына больше значения ключа отца.
Например, узлы дерева имеют значения 6, 21, 48, 49, 52, 86, 101.
Бинарное дерево будет иметь вид:
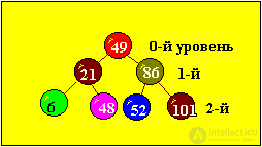
Получили упорядоченное бинарное дерево с минимальным числом уровней.
Идеально сбалансированное дерево - это дерево, в котором левое и правое поддеревья имеют уровни, отличающиеся не больше, чем на единицу.
Для построения дерева необходимо создать в памяти ЭВМ элемент следующего типа:
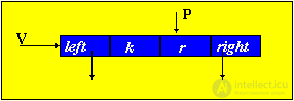
P, Q - рабочие указатели
V=maketree(key,rec) - процедура, которая создает сегмент ключа и записи
P=getnode - генерация нового элемента
tree - указатель на корень дерева
Введем сначала первое значение ключа, потом сгенерируем сам элемент узла дерева процедурой maketree. Об этом говорит сайт https://intellect.icu . Далее идем по циклу до тех пор, пока указатель не передвинется на нулевое значение.
Пусть задано бинарное дерево :

Существуют три принципа обхода бинарных деревьев. Рассмотрим их на примере заданного дерева :
Наиболее часто применяется 2-ой способ, узлы посещаются в порядке возрастания значения их ключа.
Рекурсивные процедуры обхода дерева :
1) PROCEDURE pretrave (tree)
2) PROCEDURE intrave (tree)
3) PROCEDURE postrave (tree)
Назначение этой процедуры в том, чтобы по заданному ключу осуществить поиск узла дерева. Длительность операции поиска (число узлов, которое надо перебрать для этой цели) зависит от структуры дерева. Действительно, дерево может быть вырождено в однонаправленный список (иметь единственную ветвь) - такое дерево может возникнуть, если элементы поступали в дерево в порядке возрастания (убывания) их ключей, например :

В этом случае время поиска будет такое же, как и в однонаправленном списке, т.е. в среднем придется перебрать N/2 элементов.
Наибольший эффект использования дерева достигается в том случае, когда дерево "сбалансировано". В этом случае для поиска придется перебрать не более LOG2N элементов.
Опишем процедуру поиска. Переменной search будет присваиваться указатель на найденное звено :
Для включения новой записи в дерево прежде всего нужно найти тот его узел, к которому можно "подвесить" (присоединить) новый элемент. Алгоритм поиска нужного узла тот же самый, что и при поиске узла с заданным ключом. Этот узел будет найден в тот момент, когда в качестве очередной ссылки, определяющей ветвь дерева, в которой надо продолжить поиск, окажется ссылка NIL.
Однако непосредственно использовать описанную выше процедуру поиска нельзя, потому что по окончании вычисления ее значения не фиксируется тот узел, из которого была выбрана ссылка NIL.
Модифицируем описание процедуры поиска так, чтобы в качестве ее побочного эффекта фиксировалась ссылка на узел, в котором был найден заданный ключ (в случае успешного поиска), или ссылка на узел, после обработки которого поиск прекращен (в случае неуспешного поиска). И опишем процедуру включения элемента в дерево, учитывая, что в дереве нет узла с тем же ключом, что и у включаемого элемента.
Удаление узла не должно нарушать упорядоченность дерева. При удалении элемента из бинарного дерева с заданным ключом различают три случая :
1) удаляемый узел является листом, в этом случае он просто удаляется, не нарушая этим упорядоченность дерева ;
2) если удаляемый узел имеет только одного сына, то сын перемещается на место удаляемого отца ;

Разработаем алгоритм для 3-его случая (вершина-узел имеет 2-х сыновей), вместо удаляемого узла поставим его приемника в симметричном обходе. Предшественником удаляемого узла 12 является самый правый узел левого поддерева - узел 11, а приемником или последователем при симметричном обходе (обход слева направо) является самый левый узел правого поддерева - узел 13.
Будем использовать следующие указатели :
1) Процедурой поиска элемента находим удаляемый элемент. Указатель p указывает на удаляемый элемент.
2) Установим указатель v на узел, который будет замещать удаляемый элемент.
Варианты:
1.Описать процедуру или функцию, которая:
2. Вершины дерева вещественные числа. Описать процедуру или функцию, которая:
3. Записи вершин дерева - вещественные числа. Описать процедуру, которая удаляет все вершины с отрицательными записями.
4. Записи вершин дерева - вещественные числа. Описать процедуру или функцию, которая:
5. Описать процедуру или функцию, которая:
6. Описать процедуру или функцию, которая:
7. Описать процедуру СОРY(Т,Т1), которая строит Т1 - копию дерева Т.
8. Описать процедуру ЕQUAL(T1,T2), проверяющую на равенство деревья Т1 и Т2 (деревья равны, если ключи и записи вершин одного дерева равны соответственно ключам и записям другого дерева).
9. Описать процедуру или функцию, которая:
10. Описать процедуру, которая:
a) присваивает переменной b типа char значение:
b) распечатывает атрибуты всех вершин дерева.
11. Описать процедуру или функцию, которая:
12. Описать процедуру или функцию, которая:
На этом все! Теперь вы знаете все про бинарные деревья, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое бинарные деревья и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Структуры данных
Комментарии
Оставить комментарий
Структуры данных
Термины: Структуры данных