Вам бонус- начислено 1 монета за дневную активность. Сейчас у вас 1 монета

Дерево двоичного поиска и обход дерева - Inorder, Preorder, Postorder реализация

Лекция



Привет, сегодня поговорим про дерево двоичного поиска, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое дерево двоичного поиска, обход дерева, binary search tree, tree traversal , настоятельно рекомендую прочитать все из категории Структуры данных.

обход дерева (известный также как поиск по дереву) — вид обхода графа[en], обусловливающий процесс посещения (проверки и/или обновления) каждого узла структуры дерева данных ровно один раз. Такие обходы классифицируются по порядку, в котором узлы посещаются. Алгоритмы в статье относятся к двоичным деревьям, но могут быть обобщены и для других деревьев.

Типы обхода деревьев

В отличие от связных списков, одномерных массивов и других линейных структур данных, которые канонически обходятся в линейном порядке, деревья можно обходить различными путями. Деревья можно обходить «в глубину» или «в ширину». Существует три основных способа обхода «в глубину»

  • прямой (pre-order)
  • центрированный (in-order)
  • обратный (post-order) . Кроме этих трех основных схем, возможны более сложные гибридные схемы, такие как алгоритмы поиска с ограниченной глубиной[en], подобные поиску в глубину с итеративным углублением[en]

Большинство студентов, только что окончивших инженерные специальности, или тех, кто еще учится, будут иметь свежую концепцию бинарных деревьев поиска. Но большинство людей, которые уже много лет не учились в колледже, будут иметь не очень ясное представление о деревьях двоичного поиска, если только они не использовали его или связанные с ним концепции в своей работе. В этом руководстве я покажу, как реализовать дерево двоичного поиска (BST) в Java, а также покажу следующие операции:

  1. Вставка / построение BST
  2. Нахождение узла максимального значения в BST
  3. Нахождение узла минимального значения в BST
  4. Inorder Traversal of BST
  5. Предварительный просмотр BST
  6. Постордерный обход BST

Что такое двоичное дерево поиска (BST)?

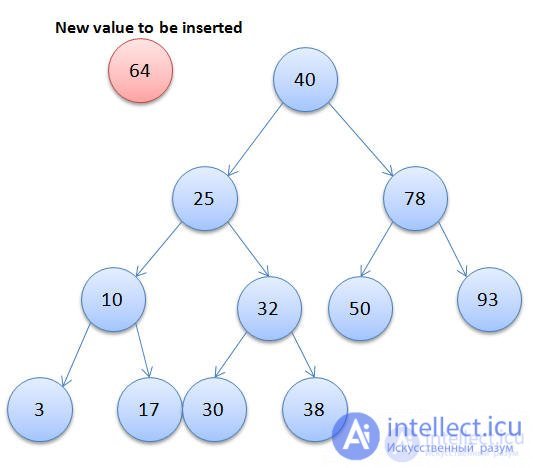
Дерево двоичного поиска (BST) - это структура данных двоичного дерева со специальной функцией, в которой в хранилище значений на каждом узле больше или равно значению, хранящемуся в его левом дочернем дочернем элементе, и меньше, чем значение, хранящееся в его правом дочернем дочернем элементе. Давайте посмотрим на пример BST:

Дерево двоичного поиска и обход дерева - Inorder, Preorder, Postorder реализация

В приведенном выше примере вы можете видеть, что в каждом узле значение в левом дочернем узле меньше или равно значению в узле, а значение в правом дочернем элементе больше, чем значение в узле.

Построение двоичного дерева поиска (BST)

Теперь, когда мы увидели, как выглядит BST, позвольте мне показать вам, как можно построить BST и вставить узлы в дерево, реализовав алгоритм на Java. Основная идея заключается в том, что на каждом узле мы сравниваем с вставляемым значением. Если значение меньше, мы проходим через левое поддерево, а если значение больше, мы проходим через правое поддерево. Предположим, нам нужно вставить значение 64 в приведенный выше BST, давайте посмотрим на узлы, пройденные до того, как оно было вставлено в нужное место:

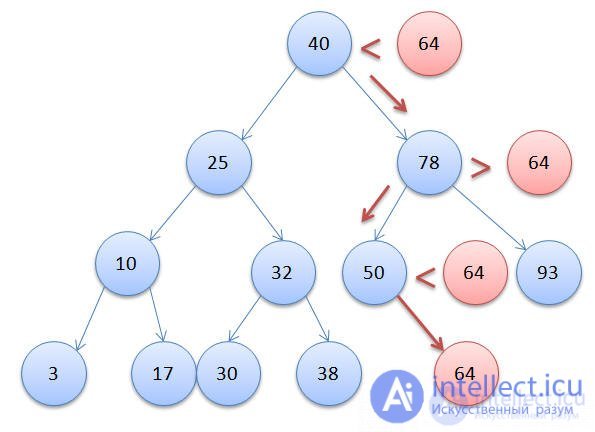
Дерево двоичного поиска и обход дерева - Inorder, Preorder, Postorder реализация

Дерево двоичного поиска и обход дерева - Inorder, Preorder, Postorder реализация

Каждый узел в BST представлен следующим java-классом:

1 public class Node {
2 public int value;
3 public Node left;
4 public Node right;
5
6 public Node(int value) {
7 this.value = value;
8 }
9
10 }

Давайте посмотрим на код на Java для достижения вышеуказанной логики:

1 public class BinarySearchTree {
2 public Node root;
3
4 public void insert(int value){
5 Node node = new Node<>(value);
6
7 if ( root == null ) {
8 root = node;
9 return;
10 }
11
12 insertRec(root, node);
13
14 }
15
16 private void insertRec(Node latestRoot, Node node){
17
18 if ( latestRoot.value > node.value){
19
20 if ( latestRoot.left == null ){
21 latestRoot.left = node;
22 return;
23 }
24 else{
25 insertRec(latestRoot.left, node);
26 }
27 }
28 else{
29 if (latestRoot.right == null){
30 latestRoot.right = node;
31 return;
32 }
33 else{
34 insertRec(latestRoot.right, node);
35 }
36 }
37 }
38 }

Нахождение максимального и минимального значения в BST

Если вы заметили в приведенном выше примере, что крайний левый узел имеет наименьшее значение, а крайний правый узел имеет наибольшее значение. Это связано с сортированным характером дерева.

Дерево двоичного поиска и обход дерева - Inorder, Preorder, Postorder реализация

Дерево двоичного поиска и обход дерева - Inorder, Preorder, Postorder реализация

Используя этот принцип, приведенные ниже методы возвращают нам самое низкое и самое высокое значение в дереве двоичного поиска:

1 /**
2 * Returns the minimum value in the Binary Search Tree.
3 */
4 public int findMinimum(){
5 if ( root == null ){
6 return 0;
7 }
8 Node currNode = root;
9 while(currNode.left != null){
10 currNode = currNode.left;
11 }
12 return currNode.value;
13 }
14
15 /**
16 * Returns the maximum value in the Binary Search Tree
17 */
18 public int findMaximum(){
19 if ( root == null){
20 return 0;
21 }
22
23 Node currNode = root;
24 while(currNode.right != null){
25 currNode = currNode.right;
26 }
27 return currNode.value;
28 }

Обход двоичного дерева поиска (BST)

Обход дерева или BST в этом случае - это посещение каждого из узлов, присутствующих в дереве, и выполнение некоторой операции со значением, присутствующим в узле, который в этом случае будет печатать значение, присутствующее в узле. Когда мы проходим по дереву, мы должны посетить значение, присутствующее в узле, затем правое поддерево узла и левое поддерево . Посещение правого и левого поддерева будет рекурсивной операцией. Порядок, в котором мы выполняем три операции, т.е. посещение значения, правого поддерева и левого поддерева, дает три метода обхода:

  1. Inorder Traversal
  2. Предварительный заказ
  3. Пост порядковый обход

Inorder Traversal

При этом обходе сначала посещается левое поддерево данного узла, затем печатается значение в данном узле, а затем посещается правое поддерево данного узла. Этот процесс рекурсивно применяется ко всем узлам в дереве, пока либо левое поддерево не станет пустым, либо правое поддерево не станет пустым.

Дерево двоичного поиска и обход дерева - Inorder, Preorder, Postorder реализация

Применяя обход Inorder для данного примера, мы получаем: 3, 10, 17, 25, 30, 32, 38, 40, 50, 78, 78, 93.

1 /**
2 * Printing the contents of the tree in an inorder way.
3 */
4 public void printInorder(){
5 printInOrderRec(root);
6 System.out.println("");
7 }
8
9 /**
10 * Helper method to recursively print the contents in an inorder way
11 */
12 private void printInOrderRec(Node currRoot){
13 if ( currRoot == null ){
14 return;
15 }
16 printInOrderRec(currRoot.left);
17 System.out.print(currRoot.value+", ");
18 printInOrderRec(currRoot.right);
19 }

Обход предзаказа

В этом обходе сначала печатается значение в данном узле, затем посещается левое поддерево данного узла, а затем посещается правое поддерево данного узла. Об этом говорит сайт https://intellect.icu . Этот процесс рекурсивно применяется ко всем узлам в дереве, пока либо левое поддерево не станет пустым, либо правое поддерево не станет пустым.

Дерево двоичного поиска и обход дерева - Inorder, Preorder, Postorder реализация

Применяя обход Preorder для данного примера, мы получаем: 40, 25, 10, 3, 17, 32, 30, 38, 78, 50, 78, 93.

1 /**
2 * Printing the contents of the tree in a Preorder way.
3 */
4 public void printPreorder() {
5 printPreOrderRec(root);
6 System.out.println("");
7 }
8
9 /**
10 * Helper method to recursively print the contents in a Preorder way
11 */
12 private void printPreOrderRec(Node currRoot) {
13 if (currRoot == null) {
14 return;
15 }
16 System.out.print(currRoot.value + ", ");
17 printPreOrderRec(currRoot.left);
18 printPreOrderRec(currRoot.right);
19 }

Пост порядковый обход

При этом обходе сначала просматривается левое поддерево данного узла, затем обходится правое поддерево данного узла, а затем печатается значение в данном узле. Этот процесс рекурсивно применяется ко всем узлам в дереве, пока либо левое поддерево не станет пустым, либо правое поддерево не станет пустым.

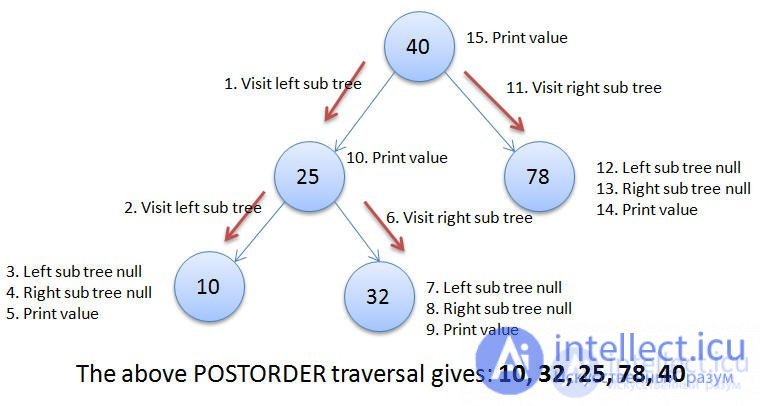
Дерево двоичного поиска и обход дерева - Inorder, Preorder, Postorder реализация

Применяя обход Postorder для данного примера, мы получаем: 3, 17, 10, 30, 38, 32, 25, 50, 93, 78, 78, 40.

1 /**
2 * Printing the contents of the tree in a Postorder way.
3 */
4 public void printPostorder() {
5 printPostOrderRec(root);
6 System.out.println("");
7 }
8
9 /**
10 * Helper method to recursively print the contents in a Postorder way
11 */
12 private void printPostOrderRec(Node currRoot) {
13 if (currRoot == null) {
14 return;
15 }
16 printPostOrderRec(currRoot.left);
17 printPostOrderRec(currRoot.right);
18 System.out.print(currRoot.value + ", ");
19
20 }

Полный код, который строит дерево для примера, описанного в этом коде, и распечатывает максимальное, минимальное значение, обход порядка, обход предварительного заказа и обход пост-заказа, можно найти ниже:

посмотреть источник
Распечатать?
1 /**
2 * Represents a node in the Binary Search Tree.
3 */
4 public class Node {
5 //The value present in the node.
6 public int value;
7
8 //The reference to the left subtree.
9 public Node left;
10
11 //The reference to the right subtree.
12 public Node right;
13
14 public Node(int value) {
15 this.value = value;
16 }
17
18 }
19
20 /**
21 * Represents the Binary Search Tree.
22 */
23 public class BinarySearchTree {
24
25 //Refrence for the root of the tree.
26 public Node root;
27
28 public BinarySearchTree insert(int value) {
29 Node node = new Node<>(value);
30
31 if (root == null) {
32 root = node;
33 return this;
34 }
35
36 insertRec(root, node);
37 return this;
38 }
39
40 private void insertRec(Node latestRoot, Node node) {
41
42 if (latestRoot.value > node.value) {
43
44 if (latestRoot.left == null) {
45 latestRoot.left = node;
46 return;
47 } else {
48 insertRec(latestRoot.left, node);
49 }
50 } else {
51 if (latestRoot.right == null) {
52 latestRoot.right = node;
53 return;
54 } else {
55 insertRec(latestRoot.right, node);
56 }
57 }
58 }
59
60 /**
61 * Returns the minimum value in the Binary Search Tree.
62 */
63 public int findMinimum() {
64 if (root == null) {
65 return 0;
66 }
67 Node currNode = root;
68 while (currNode.left != null) {
69 currNode = currNode.left;
70 }
71 return currNode.value;
72 }
73
74 /**
75 * Returns the maximum value in the Binary Search Tree
76 */
77 public int findMaximum() {
78 if (root == null) {
79 return 0;
80 }
81
82 Node currNode = root;
83 while (currNode.right != null) {
84 currNode = currNode.right;
85 }
86 return currNode.value;
87 }
88
89 /**
90 * Printing the contents of the tree in an inorder way.
91 */
92 public void printInorder() {
93 printInOrderRec(root);
94 System.out.println("");
95 }
96
97 /**
98 * Helper method to recursively print the contents in an inorder way
99 */
100 private void printInOrderRec(Node currRoot) {
101 if (currRoot == null) {
102 return;
103 }
104 printInOrderRec(currRoot.left);
105 System.out.print(currRoot.value + ", ");
106 printInOrderRec(currRoot.right);
107 }
108
109 /**
110 * Printing the contents of the tree in a Preorder way.
111 */
112 public void printPreorder() {
113 printPreOrderRec(root);
114 System.out.println("");
115 }
116
117 /**
118 * Helper method to recursively print the contents in a Preorder way
119 */
120 private void printPreOrderRec(Node currRoot) {
121 if (currRoot == null) {
122 return;
123 }
124 System.out.print(currRoot.value + ", ");
125 printPreOrderRec(currRoot.left);
126 printPreOrderRec(currRoot.right);
127 }
128
129 /**
130 * Printing the contents of the tree in a Postorder way.
131 */
132 public void printPostorder() {
133 printPostOrderRec(root);
134 System.out.println("");
135 }
136
137 /**
138 * Helper method to recursively print the contents in a Postorder way
139 */
140 private void printPostOrderRec(Node currRoot) {
141 if (currRoot == null) {
142 return;
143 }
144 printPostOrderRec(currRoot.left);
145 printPostOrderRec(currRoot.right);
146 System.out.print(currRoot.value + ", ");
147
148 }
149 }
150
151 public class BinarySearchTreeDemo {
152
153 public static void main(String[] args) {
154 BinarySearchTree bst = new BinarySearchTree();
155 bst .insert(40)
156 .insert(25)
157 .insert(78)
158 .insert(10)
159 .insert(3)
160 .insert(17)
161 .insert(32)
162 .insert(30)
163 .insert(38)
164 .insert(78)
165 .insert(50)
166 .insert(93);
167 System.out.println("Inorder traversal");
168 bst.printInorder();
169
170 System.out.println("Preorder Traversal");
171 bst.printPreorder();
172
173 System.out.println("Postorder Traversal");
174 bst.printPostorder();
175
176 System.out.println("The minimum value in the BST: " + bst.findMinimum());
177 System.out.println("The maximum value in the BST: " + bst.findMaximum());
178
179 }
180 }
Дерево двоичного поиска и обход дерева - Inorder, Preorder, Postorder реализация
Обход дерева.
Вам предлагается решить эту задачу в соответствии с описанием задачи, используя любой язык, который вы знаете.

Реализуйте двоичное дерево, в котором каждый узел несет целое число, и реализуйте обход до, в порядке, после и в порядке уровней. Используйте эти обходы для вывода следующего дерева:

         1
        / \
       / \
      / \
     2 3
    / \ /
   4 5 6
  / / \
 7 8 9

Правильный вывод должен выглядеть так:

предзаказ: 1 2 4 7 5 3 6 8 9
порядок: 7 4 2 5 1 8 6 9 3
отправитель: 7 4 5 2 8 9 6 3 1
порядок уровней: 1 2 3 4 5 6 7 8 9

На этом все! Теперь вы знаете все про дерево двоичного поиска, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое дерево двоичного поиска, обход дерева, binary search tree, tree traversal и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Структуры данных

создано: 2014-12-05
обновлено: 2024-11-14
467

Рейтиг 9 of 10. count vote: 2
Вы довольны ?:
Поделиться:

Найди готовое или заработай

С нашими удобными сервисами без комиссии*

Как это работает? | Узнать цену?

Найти исполнителя
$0 / весь год.
  • У вас есть задание, но нет времени его делать
  • Вы хотите найти профессионала для выплнения задания
  • Возможно примерение функции гаранта на сделку
  • Приорететная поддержка
  • идеально подходит для студентов, у которых нет времени для решения заданий
Создать заявку
Готовое решение
$0 / весь год.
  • Вы можите продать(исполнителем) или купить(заказчиком) готовое решение
  • Вам предоставят готовое решение
  • Будет предоставлено в минимальные сроки т.к. задание уже готовое
  • Вы получите базовую гарантию 8 дней
  • Вы можете заработать на материалах
  • подходит как для студентов так и для преподавателей
Добавить решение
Я исполнитель
$0 / весь год.
  • Вы профессионал своего дела
  • У вас есть опыт и желание зарабатывать
  • Вы хотите помочь в решении задач или написании работ
  • Возможно примерение функции гаранта на сделку
  • подходит для опытных студентов так и для преподавателей
Разместить резюме

Комментарии

Оставить комментарий
Если у вас есть какое-либо предложение, идея, благодарность или комментарий, не стесняйтесь писать. Мы очень ценим отзывы и рады услышать ваше мнение.
To reply

Структуры данных

Термины: Структуры данных