Лекция
Привет, Вы узнаете о том , что такое анализ чувствительности, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое анализ чувствительности, анализ чувствительности системы, анализ чувствительности модели, анализ чувствительности проекта , настоятельно рекомендую прочитать все из категории Моделирование и Моделирование систем.
анализ чувствительности (англ. sensitivity analysis) — оценка влияния изменения исходных параметров проекта на его конечные характеристики, в качестве которых, обычно, используется внутренняя норма прибыли или NPV. Техника проведения анализа чувствительности состоит в изменении выбранных параметров в определенных пределах, при условии, что остальные параметры остаются неизменными. Чем больше диапазон вариации параметров, при котором NPV или норма прибыли остается положительной величиной, тем устойчивее проект. анализ чувствительности проекта позволяет оценить, как изменяются результирующие показатели реализации проекта при различных значениях заданных переменных, необходимых для расчета. Этот вид анализа позволяет определить наиболее критические переменные, которые в наибольшей степени могут повлиять на осуществимость и эффективность проекта.
В математическом моделировании показателем чувствительности переменной отклика (yi) к параметру (kj) служит величина 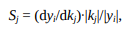 , называемая «чувствительностью к параметру» [Рыжова, 2006: с. 21].
, называемая «чувствительностью к параметру» [Рыжова, 2006: с. 21].
Анализ чувствительности - это исследование того, как неопределенность на выходе математической модели или системы (числовой или иной) может быть разделена и отнесена к различным источникам неопределенности на ее входных данных. Смежной практикой является анализ неопределенности , в котором больше внимания уделяется количественной оценке неопределенности и распространению неопределенности ; в идеале анализ неопределенности и чувствительности следует проводить одновременно.
Анализ чувствительности инвестиционного проекта (sensitivity analysis) – это оценка влияния изменения исходных параметров инвестиционного проекта (инвестиционные затраты, приток денежных средств, ставка дисконтирования, операционные расходы и т. д.) на его конечные характеристики, в качестве которых, как правило, используется IRR или NPV.
анализ чувствительности системы можно выполнить, например, при помощи метода деревьев отказов или Д-фактором. .
анализ чувствительности модели определяет оценку влияния колебаний значений входных переменных на отклики (выходные) характеристики модели . Необходимо установить, при каком разбросе входных данных сохраняется справедливость основных выводов, сделанных по результатам моделирования.
Под анализом чувствительности понимается определение чувствительности наших окончательных результатов моделирования к изменению используемых значение входных переменных и параметров модели. Анализ определяет, как меняется выходная переменная У при небольших изменениях различных параметров модели или ее входов X.
Простота проведения анализа чувствительности в имитационном моделировании — одно из преимуществ этого метода. Оценка чувствительности является исключительно важной процедурой и подготовительным этапом перед планированием имитационного эксперимента.
Процесс пересчета результатов при альтернативных допущениях для определения влияния переменной при анализе чувствительности может быть полезен для ряда целей , включая:
При изучении чувствительности моделей возникают три типа задач [Пененко, 1981, с. 9]:
Согласно профессору Энтони Аткинсону анализ чувствительности — это анализ влияния изменения параметра на решение, а не на результат . Английский профессор Колин Друри дополняет: анализ чувствительности оценивает насколько чистая приведенная стоимость реагирует на изменения переменных, которые используются для ее вычисления .
взаимоотношения между входами и выходами , может быть плохо изучена. В таких случаях модель можно рассматривать как черный ящик , т.е. выход является «непрозрачной» функцией своих входов.
Довольно часто некоторые или все входные данные модели подвержены источникам неопределенности , включая ошибки измерения , отсутствие информации и плохое или частичное понимание движущих сил и механизмов. Эта неопределенность накладывает ограничения на нашу уверенность в ответе или выходе модели. Кроме того, моделям, возможно, придется справляться с естественной внутренней изменчивостью системы (случайной), такой как возникновение стохастических событий.
Хорошая практика моделирования требует, чтобы разработчик модели дал оценку достоверности модели. Это требует, во-первых, количественной оценки неопределенности любых результатов модели ( анализ неопределенности ); и во-вторых, оценка того, насколько каждый вход вносит вклад в неопределенность выхода. Анализ чувствительности обращается ко второму из этих вопросов (хотя анализ неопределенности обычно является необходимым предвестником), выполняя роль упорядочения по важности силы и релевантности входных данных при определении вариации выходных данных.
В моделях, включающих множество входных переменных, анализ чувствительности является важным элементом построения модели и обеспечения качества. Национальные и международные агентства, участвующие в исследованиях по оценке воздействия , включили в свои руководящие принципы разделы, посвященные анализу чувствительности. Примерами являются Европейская комиссия (см., Например, руководящие принципы оценки воздействия ), Управление и бюджет Белого дома , Межправительственная группа экспертов по изменению климата и руководящие принципы моделирования Агентства по охране окружающей среды США . В комментарии, опубликованном в 2020 году в журнале Nature 22, ученые считаютCOVID-19 как повод предложить пять способов заставить модели лучше служить обществу. Одна из пяти рекомендаций под заголовком «Помните о допущениях» - это «выполнить глобальный анализ неопределенности и чувствительности, [...] позволяющий всему, что является неопределенным - переменным, математическим отношениям и граничным условиям - одновременно изменяться в ходе выполнения модель производит свой диапазон прогнозов ».
Согласно профессору Энтони Аткинсону анализ «что, если» — это анализ, который исследует влияние изменения параметра на результат .
В качестве варьируемых исходных переменных принимают:
Анализ чувствительности может выполняться в различных формах :
Результаты анализа чувствительности приводятся в табличной или графической формах. Последняя является более наглядной и применяется в презентационных целях.
При анализе экономической эффективности инвестиционного проекта необходимо учитывать его неопределенность (неполноту и неточность информации об условиях реализации проекта), и риск (возможность возникновения таких условий, которые приведут к негативным последствиям для всех или отдельных участников проекта). Учет фактор неопределенности и оценку рисков проекта обеспечивает анализ чувствительности.
Анализ чувствительности инвестиционного проекта (sensitivity analysis) – это оценка влияния изменения исходных параметров инвестиционного проекта (инвестиционные затраты, приток денежных средств, ставка дисконтирования, операционные расходы и т. д.) на его конечные характеристики, в качестве которых, как правило, используется IRR или NPV.
Далее оценивается относительное изменение критерия по отношению к базисному случаю и рассчитывается показатель чувствительности.В ходе анализа чувствительности инвестиционного проекта, сначала определяются исходные параметры (показатели), по которым производят расчет чувствительности инвестпроекта. Затем осуществляют последовательно-единичное изменение каждого выбранного показателя. Только одна из переменных меняет свое значение на прогнозное число процентов (как правило, 1%, 5% или 10%), и на этой основе пересчитывается новая величина используемого критерия (например, NPV или IRR).
Показатель чувствительности это отношение процентного изменения критерия к изменению значения переменной на прогнозное число процентов (эластичность изменения показателя). Аналогично рассчитываются показатели чувствительности по каждой из остальных выбранных переменных.
На следующем этапе, используя результаты выполненных расчетов, производят ранжирование параметров по степени важности (к примеру, очень высокая, средняя и невысокая) и осуществляют и экспертную оценку предсказуемости (прогнозируемости) значений показателей (высокая, средняя или низкая).
Для анализа чувствительности инвестиционного проекта главное – это оценить степень влияния изменения каждого (или их комбинации) из исходных параметров, чтобы предусмотреть наихудшее развитие ситуации в инвестиционном проекте.
В первом случае формируются 3—5 сценариев развития проекта. Об этом говорит сайт https://intellect.icu . Каждому сценарию должны соответствовать:
В результате расчета определяются средние (с учетом вероятности наступления каждого сценария) значения результирующих показателей.
Выбор метода анализа чувствительности обычно продиктован рядом ограничений или настроек проблемы. Некоторые из наиболее распространенных:
Вычислительные затраты - проблема многих практических анализов чувствительности. Некоторые методы снижения вычислительных затрат включают использование эмуляторов (для больших моделей) и методов скрининга (для уменьшения размерности проблемы). Другой метод - использовать метод анализа чувствительности на основе событий для выбора переменных для приложений с ограничениями по времени. [12]Это метод выбора входной переменной (IVS), который собирает вместе информацию о трассировке изменений входных и выходных данных системы с использованием анализа чувствительности для создания матрицы триггеров / событий входа / выхода, которая предназначена для сопоставления взаимосвязей между входными данными как причин. которые запускают события, и выходные данные, описывающие фактические события. Причинно-следственная связь между причинами изменения состояния, то есть входными переменными, и выходными параметрами системы эффектов определяет, какой набор входов действительно влияет на данный выход. Метод имеет явное преимущество перед аналитическим и вычислительным методом IVS, поскольку он пытается понять и интерпретировать изменение состояния системы в кратчайшие сроки с минимальными вычислительными затратами. [12] [13]
В анализе неопределенности и чувствительности существует решающий компромисс между тем, насколько скрупулезно аналитик исследует исходные предположения и насколько широкими могут быть полученные выводы . Это хорошо иллюстрирует эконометрист Эдвард Э. Лимер : [16] [17]
Я предложил форму организованного анализа чувствительности, которую я называю «анализом глобальной чувствительности», в котором выбирается ряд альтернативных допущений и определяется соответствующий интервал выводов. Выводы считаются надежными только в том случае, если область допущений достаточно широка, чтобы вызывать доверие, а соответствующий интервал выводов достаточно узок, чтобы быть полезными.
Некоторые общие трудности при анализе чувствительности включают:
Идеальная схема анализа чувствительности, возможно, на основе выборки. Неопределенность, возникающая из различных источников - ошибок в данных, процедуры оценки параметров, альтернативных структур модели - распространяется через модель для анализа неопределенности, и их относительная важность оценивается количественно с помощью анализа чувствительности.
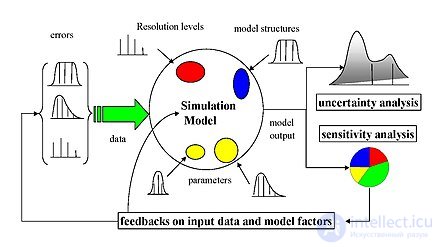
Выборочный анализ чувствительности по диаграммам рассеяния. Y (вертикальная ось) является функцией четырех факторов. Точки на четырех диаграммах рассеяния всегда одинаковы, хотя отсортированы по-разному, то есть по Z 1 , Z 2 , Z 3 , Z 4 по очереди. Обратите внимание, что абсцисса различна для каждого графика: (-5, +5) для Z 1 , (-8, +8) для Z 2 , (-10, +10) для Z 3 и Z 4 . Z 4 является наиболее важным в оказании влияния на Y , как он придает более «форму» на Y .
Существует множество подходов к выполнению анализа чувствительности, многие из которых были разработаны для устранения одного или нескольких ограничений, описанных выше. Они также различаются по типу меры чувствительности, будь то на основе (например) разложения дисперсии , частных производных или элементарных эффектов . Однако в целом большинство процедур придерживаются следующей схемы:
В некоторых случаях эта процедура будет повторяться, например, в задачах большой размерности, когда пользователь должен отсеивать неважные переменные перед выполнением полного анализа чувствительности.
Различные типы «основных методов» (обсуждаемых ниже) различаются по различным рассчитываемым показателям чувствительности. Эти категории могут как-то пересекаться. Могут быть предложены альтернативные способы получения этих показателей с учетом ограничений проблемы.
Затем чувствительность может быть измерена путем отслеживания изменений на выходе, например, с помощью частных производных или линейной регрессии.. Это кажется логичным подходом, поскольку любое изменение, наблюдаемое в выходных данных, однозначно будет связано с изменением одной переменной. Более того, изменяя одну переменную за раз, можно сохранить все остальные переменные фиксированными на их центральных или базовых значениях. Это увеличивает сопоставимость результатов (все «эффекты» вычисляются относительно одной и той же центральной точки в пространстве) и сводит к минимуму вероятность сбоев компьютерной программы, что более вероятно при одновременном изменении нескольких входных факторов. Специалисты по моделированию часто предпочитают OAT по практическим причинам. В случае отказа модели при анализе OAT разработчик модели сразу знает, какой входной фактор является причиной отказа. [14]
Однако, несмотря на свою простоту, этот подход не полностью исследует входное пространство, так как он не принимает во внимание одновременное изменение входных переменных. Это означает, что подход OAT не может обнаружить наличие взаимодействий между входными переменными. [26]
Методы, основанные на локальной производной, включают взятие частной производной выхода Y по входному фактору X i :
где нижний индекс X 0 указывает, что производная берется в некоторой фиксированной точке в пространстве ввода (отсюда «локальный» в имени класса). Сопряженное моделирование [27] [28] и Автоматическое дифференцирование [29] являются методами этого класса. Подобно OAT, локальные методы не пытаются полностью исследовать входное пространство, поскольку они исследуют небольшие возмущения, обычно по одной переменной за раз.
Регрессионный анализ в контексте анализа чувствительности включает подгонку линейной регрессии к ответу модели и использование стандартизованных коэффициентов регрессии в качестве прямых мер чувствительности. Регрессия должна быть линейной по отношению к данным (т. Е. Гиперплоскостью, следовательно, без квадратичных членов и т. Д. В качестве регрессоров), потому что в противном случае трудно интерпретировать стандартизованные коэффициенты. Поэтому этот метод наиболее подходит, когда реакция модели на самом деле линейна; линейность может быть подтверждена, например, если коэффициент детерминации велик. Преимущества регрессионного анализа заключаются в том, что он прост и имеет низкие вычислительные затраты.
Методы, основанные на дисперсии [30] [31] [32], представляют собой класс вероятностных подходов, которые количественно определяют входные и выходные неопределенности как распределения вероятностей и разлагают выходную дисперсию на части, относящиеся к входным переменным и комбинациям переменных. Таким образом, чувствительность выхода к входной переменной измеряется величиной отклонения выхода, вызванной этим входом. Их можно выразить как условные ожидания, т. Е. Рассматривая модель Y = f ( X ) для X = { X 1 , X 2 , ... X k }, меру чувствительностиi- я переменная X i задается как,
Методы, основанные на дисперсии, позволяют полностью исследовать входное пространство, учитывать взаимодействия и нелинейные ответы. По этим причинам они широко используются, когда их можно рассчитать. Обычно этот расчет включает использование методов Монте-Карло , но, поскольку это может включать многие тысячи прогонов модели, при необходимости можно использовать другие методы (например, эмуляторы) для уменьшения вычислительных затрат. Обратите внимание, что полное разложение дисперсии имеет смысл только в том случае, если входные факторы не зависят друг от друга. [33]
Одним из основных недостатков предыдущих методов анализа чувствительности является то, что ни один из них не учитывает пространственно упорядоченную структуру поверхности отклика / выходных данных модели Y = f ( X ) в пространстве параметров. Используя концепции направленных вариограмм и ковариограмм, вариограммный анализ поверхностей отклика (VARS) устраняет этот недостаток путем распознавания пространственно непрерывной корреляционной структуры для значений Y , а следовательно, и для значений.
В основном, чем выше изменчивость, тем более неоднородной является поверхность отклика по определенному направлению / параметру при определенном масштабе возмущения. Соответственно, в рамках VARS значения направленных вариограмм для заданного масштаба возмущения можно рассматривать как исчерпывающую иллюстрацию информации о чувствительности, связывая анализ вариограмм с концепциями как направления, так и масштаба возмущения. В результате структура VARS учитывает тот факт, что чувствительность зависит от масштаба, и, таким образом, преодолевает проблему масштабирования традиционных методов анализа чувствительности. [36]Что еще более важно, VARS может обеспечить относительно стабильные и статистически надежные оценки чувствительности параметров с гораздо меньшими вычислительными затратами, чем другие стратегии (примерно на два порядка эффективнее). [37] Примечательно, что было показано, что существует теоретическая связь между структурой VARS и подходами, основанными на дисперсии и производной.
Скрининг - это частный случай метода, основанного на выборке. Задача здесь скорее состоит в том, чтобы определить, какие входные переменные вносят значительный вклад в неопределенность выходных данных в моделях с высокой размерностью, а не в точном количественном определении чувствительности (т.е. в терминах дисперсии). Скрининг, как правило, имеет относительно низкие вычислительные затраты по сравнению с другими подходами, и его можно использовать в предварительном анализе для отсеивания не влияющих переменных перед применением более информативного анализа к оставшемуся набору. Одним из наиболее часто используемых методов скрининга является метод элементарного воздействия . [38] [39]
Простой, но полезный инструмент - построить графики разброса выходной переменной по отношению к отдельным входным переменным после (случайной) выборки модели по входным распределениям. Преимущество этого подхода состоит в том, что он также может работать с «заданными данными», т. Е. Набором произвольно размещенных точек данных, и дает прямую визуальную индикацию чувствительности. Количественные показатели также могут быть получены, например, путем измерения корреляции между Y и X i или даже путем оценки показателей, основанных на дисперсии, с помощью нелинейной регрессии . [15]
Был разработан ряд методов, позволяющих преодолеть некоторые из рассмотренных выше ограничений, которые в противном случае сделали бы невозможным оценку показателей чувствительности (чаще всего из-за вычислительных затрат ). Как правило, эти методы ориентированы на эффективное вычисление показателей чувствительности на основе дисперсии.
Ясно, что суть эмуляторного подхода состоит в том, чтобы найти η (эмулятор), который является достаточно близким приближением к модели f . Это требует следующих шагов,
Выборка модели часто может быть сделана с помощью последовательностей с низким расхождением , таких как последовательность Соболя - из-за математика Ильи М. Соболя или выборки из латинского гиперкуба , хотя случайные планы также могут использоваться с потерей некоторой эффективности. Выбор типа эмулятора и обучение внутренне связаны, поскольку метод обучения будет зависеть от класса эмулятора. Некоторые типы эмуляторов, которые успешно использовались для анализа чувствительности, включают:
Использование эмулятора создает проблему машинного обучения , которая может быть трудной, если реакция модели сильно нелинейна . Во всех случаях полезно проверить точность эмулятора, например, с помощью перекрестной проверки .
Представление модели большой размерности (HDMR) [47] [48] (термин принадлежит Х. Рабицу [49]) по сути является эмуляторным подходом, который включает разложение выходных данных функции на линейную комбинацию входных членов и взаимодействий возрастающей размерности. Подход HDMR использует тот факт, что модель обычно можно хорошо аппроксимировать, пренебрегая взаимодействиями более высокого порядка (второго или третьего порядка и выше). Затем каждый член усеченного ряда может быть аппроксимирован, например, многочленами или сплайнами (REFS), а ответ выражен как сумма основных эффектов и взаимодействий до порядка усечения. С этой точки зрения HDMR можно рассматривать как эмуляторы, пренебрегающие взаимодействиями высокого порядка; Преимущество состоит в том, что они могут эмулировать модели с более высокой размерностью, чем эмуляторы полного порядка.
Представление модели большой размерности - это конечное разложение для заданной функции многих переменных . Расширение впервые описано Соболем как
Методика определения функций правой части приведена в статье Соболя. Обзор можно найти здесь: Представление многомерной модели (HDMR): концепции и приложения .
Тест амплитудной чувствительности Фурье (FAST) использует ряд Фурье для представления многомерной функции (модели) в частотной области с использованием одной частотной переменной. Следовательно, интегралы, необходимые для расчета индексов чувствительности, становятся одномерными, что приводит к экономии вычислений.
Методы, основанные на фильтрации Монте-Карло. [50] [51] Они также основаны на выборке, и здесь цель состоит в том, чтобы идентифицировать области в пространстве входных факторов, соответствующие конкретным значениям (например, высоким или низким) выходных данных.
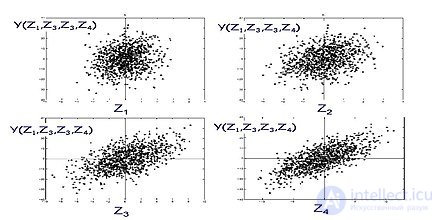
Анализ чувствительности. Результаты расчетов на листе Excel
Из расчетов и графика видно, какое именно изменение входных параметров выдерживает проект.
Анализ чувствительности имеет ограничения :
Примеры анализа чувствительности можно найти в различных областях применения, таких как:
Может случиться так, что анализ чувствительности исследования, основанного на модели, предназначен для подкрепления вывода и подтверждения его надежности в контексте, когда вывод учитывается в политике или процессе принятия решений. В этих случаях формирование самого анализа, его институциональный контекст и мотивация его автора могут стать вопросом огромной важности, а анализ чистой чувствительности - с его акцентом на параметрическую неопределенность - может считаться недостаточным. Акцент на формулировке может быть обусловлен, среди прочего, актуальностью исследования политики для различных групп интересов, для которых характерны разные нормы и ценности, и, следовательно, другой рассказ о том, «в чем проблема» и, прежде всего, о том, «кто говорит сказка'. Чаще всего фрейм включает более или менее неявные предположения,
Для того, чтобы должным образом учесть эти проблемы, инструменты SA были расширены для обеспечения оценки всего процесса создания знаний и модели. Этот подход получил название «аудит чувствительности». Он основан на NUSAP [52], методе, используемом для определения ценности количественной информации с помощью создания "родословных" чисел. Аналогичным образом, аудит чувствительности был разработан для получения родословных моделей и выводов на основе моделей. [53] Аудит чувствительности был специально разработан для состязательного контекста, когда не только характер доказательства, но также степень определенности и неопределенности, связанной с доказательствами, будет предметом партийных интересов. [54]Аудит чувствительности рекомендован в руководящих принципах Европейской комиссии по оценке воздействия , а также в отчете «Научные рекомендации по политике» Европейских академий. [55]
Исследование, описанное в статье про анализ чувствительности, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое анализ чувствительности, анализ чувствительности системы, анализ чувствительности модели, анализ чувствительности проекта и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Моделирование и Моделирование систем
Комментарии
Оставить комментарий
Моделирование и Моделирование систем
Термины: Моделирование и Моделирование систем