Лекция
Это продолжение увлекательной статьи про проектирование базы данных.
...
/>
ул.Театральная, д.15
ул.Студенческая, д.4
ул.Студенческая, д.4
Это отношение находятся во второй нормальной форме. Действительно, как это видно из диаграммы на рис.10.11, между его неключевыми атрибутами общежитие и адрес и ключом отношения, которым является атрибут КОД_СТУДЕНТА, имеет место неприводимая функциональная зависимость. Поэтому в данном отношении не может быть аномалий, связанных с наличием приводимой функциональной зависимости у отношений, не находящихся во второй нормальной форме. Тем не менее, при внимательном рассмотрении этого отношения можно увидеть, что структура отношения на рис.10.12 не лишена недостатков.
Действительно, одинаковые значения адреса общежития повторяются многократно для каждого студента, проживающего в этом общежитии. Эта избыточность также приводит к возникновению аномалий при выполнении над отношением операции обновления данных.
Операция INSERT. Мы не можем включить в базу данных информацию об адресе нового общежития до тех пор, пока у нас нет данных хотя бы об одном студенте, проживающем в этом общежитии.
Операция DELETE. При удалении информации о проживающих в общежитии студентах можно потерять информацию об адресе общежития. Например, при удалении кортежа для студента с кодом С9 мы теряем информацию об адресе общежития №2.
Операция UPDATE. Дублирование информации об адресах общежитий приводит к тому, что в случае переименования названия улицы, на которой расположено общежитие, необходимо внести изменения в адрес общежития для всех проживающих в нем студентов. При некорректном завершении такой операции в отношении могут оказаться кортежи с противоречивой информацией – для одного общежития два значения адреса, что противоречит имеющей место функциональной зависимости атрибута адрес от атрибута общежитие (см. рис. 10.11).
Очевидно, что причиной этих аномалий уже не является наличие приводимой функциональной зависимости неключевых атрибутов от ключа, как это было в примере, рассмотренном в предыдущем разделе. Таких зависимостей в этом отношении нет. Оно находится во второй нормальной форме и его неключевые атрибуты общежитие и адрес зависят от ключа (атрибут КОД_СТУДЕНТА неприводимо.
На этот раз причиной имеющих место аномалий обновления является наличие транзитивной функциональной зависимости атрибута адрес от атрибута Код_студента, показанной на рис.10.13 пунктирной стрелкой.
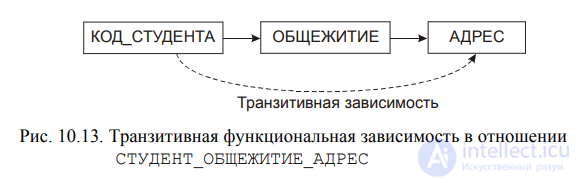
Решение обозначенной проблемы также состоит в декомпозиции отношения СТУДЕНТ_ОБЩЕЖИТИЕ_АДРЕС на два отношения для исключения транзитивной функциональной зависимости. Результатом такой декомпозиции являются два отношения, представленные вместе с диаграммами их функциональных зависимостей на рис.10.14.
|
|
Данная декомпозиция является декомпозицией без потерь. Исходное отношение может быть восстановлено путем операции соединения отношений СТУДЕНТ_ОБЩЕЖИТИЕ и ОБЩЕЖИТИЕ_АДРЕС по атрибуту общежитие. Также при декомпозиции не теряется информация о функциональной (транзитивной) зависимости КОД_СТУДЕНТА→АДРЕС, так как она может быть выведена из зависимостей КОД_СТУДЕНТА→ОБЩЕЖИТИЕ и ОБЩЕЖИТИЕ→АДРЕС.
Не трудно видеть, что данная декомпозиция решает проблемы с приведенными примерами аномалий операций обновления. Действительно, информация об адресе нового общежития может быть легко вставлена в отношение ОБЩЕЖИТИЕ_АДРЕС, операция удаления информации о студенте из отношения СТУДЕНТ_ОБЩЕЖИТИЕ не затрагивает информации об адресах общежитий, и, наконец, изменение названия улицы для общежития производится модификацией значения атрибута АДРЕС в соответствующем (единственном) кортеже отношения ОБЩЕЖИТИЕ_АДРЕС.
Декомпозиция отношения СТУДЕНТ_ОБЩЕЖИТИЕ_АДРЕС переводит его в два отношения СТУДЕНТ_ОБЩЕЖИТИЕ и ОБЩЕЖИТИЕ_АДРЕС, находящиеся уже в третьей нормальной форме. Определение этой нормальной формы имеет следующий вид.
Отношение находится в третьей нормальной форме (3НФ) тогда и только тогда, когда оно находится во второй нормальной форме и каждый его неключевой атрибут нетранзитивно зависит от потенциального ключа.
Приведенные выше отношения студент и УСПЕВАЕМОСТЬ на рис.10.9, СТУДЕНТ_ОБЩЕЖИТИЕ и ОБЩЕЖИТИЕ_АДРЕС на рис.10.14 удовлетворяют этому определению, поэтому все они находятся в третьей нормальной форме.
Говоря о декомпозиции отношения СТУДЕНТ_ОБЩЕЖИТИЕ_АДРЕС на рис.10.12 с целью преобразования его в два отношения, находящиеся в третьей нормальной форме, следует обратить внимание на то, что кроме приведенного на рис.10.14, возможен другой вариант разбиения его на два отношения. Этот вариант представлен на рис.10.15.
|
|

Рис.10.15. Другой вариант декомпозиции отношения СТУДЕНТ_ОБЩЕЖИТИЕ_АДРЕС
Можно видеть, что соединение этих двух отношений по атрибуту КОД_СТУДЕНТА обеспечивает восстановление данных исходного отношения СТУДЕНТ_ОБЩЕЖИТИЕ_АДРЕС. Существенным, однако, является то, что при такой декомпозиции в этих отношениях оказалась утраченной функциональная зависимость атрибута АДРЕС от атрибута ОБЩЕЖИТИЕ, то есть зависимость ОБЩЕЖИТИЕ→АДРЕС, имеющая место в исходном преобразуемом отношении СТУДЕНТ_ОБЩЕЖИТИЕ_АДРЕС.
В предыдущем варианте декомпозиция устраняла транзитивную функциональную зависимость, при этом информация не терялась, так как эта зависимость может быть выведена из оставшихся по правилам Армстронга (см. раздел 10.1). В рассматриваемом же варианте вместо транзитивной зависимости была потеряна зависимость ОБЩЕЖИТИЕ→АДРЕС, которая не выводится из остальных. Необходимость поддержания в базе данных такой зависимости делает в этом случае возможные изменения значений атрибутов ОБЩЕЖИТИЕ и АДРЕС, теперь находящихся в разных отношениях, зависимыми друг от друга.
Действительно, при изменении значения атрибута общежитие в каком-либо кортеже отношения студент_общежитие мы должны произвести соответствующие изменения атрибута АДРЕС в отношении СТУДЕНТ_АДРЕС. Следовательно, необходимость поддержания функциональной зависимости ОБЩЕЖИТИЕ→АДРЕС из зависимости между атрибутами одного отношения превратилась в ограничение целостности, накладываемое на два отношения и реализуемое гораздо более сложно.
При первом же варианте декомпозиции, представленном на рис.10.14, функциональная зависимость ОБЩЕЖИТИЕ →АДРЕС, порождающая в отношении СТУДЕНТ_ОБЩЕЖИТИЕ_АДРЕС нежелательную транзитивную зависимость СТУДЕНТ→АДРЕС преобразуется в отношении ОБЩЕЖИТИЕ_АДРЕС в функциональную зависимость атрибута от первичного ключа. Ограничение целостности, задаваемое такой зависимостью, в этом случае привести в действие гораздо проще. Оно автоматически обеспечивается путем наложение ограничений на уникальность первичного ключа.
Таким образом, при преобразовании отношения из второй в третью нормальную форму необходимо выбирать вариант декомпозиции с независимыми проекциями.
Риссанен (Rissanen) показал следующее.
Проекции R1 и R2 отношения R независимы в рассмотренном выше смысле тогда и только тогда, когда:
Второй вариант декомпозиции отношения СТУДЕНТ_ОБЩЕЖИТИЕ_АДРЕС, представленный на рис.10.15, не удовлетворяет правилу Риссанена, поэтому функциональная зависимость ОБЩЕЖИТИЕ→АДРЕС, имеющая место в отношении СТУДЕНТ_ОБЩЕЖИТИЕ_АДРЕС, не может быть выведена из функциональных зависимостей, имеющихся в отношениях СТУДЕНТ_ОБЩЕЖИТИЕ и СТУДЕНТ_ АДРЕС.
Еще раз обращаем внимание на то, что наличие определенных функциональных зависимостей между атрибутами отношений является отражением семантики предметной области, ее смыслового содержания и не может быть определено исходя из конкретных значений атрибутов отношений в некоторый момент времени. Другими словами, описание и обеспечение функциональных зависимостей является одной из форм ограничений целостности базы данных, которые должны выполняться при любом состоянии отношений базы данных.
В предыдущих двух разделах преобразование отношений во вторую и третью нормальную форму рассматривалось на примере отношений, имеющих единственный потенциальный (он же первичный) ключ. Для такого рода отношений преобразование в третью нормальную форму решает все приведенные выше нежелательные эффекты, связанные с ограничением функциональных зависимостей. На практике, однако, возможны более сложные случаи:
Оказывается, что в этих более сложных случаях преобразование отношений в третью нормальную форму не всегда обеспечивает решение нежелательных проблем, связанных с аномалиями операций обновления. Для их устранения была введена еще одна нормальная форма, получившая название нормальной формы Бойса – Кодда или сокращенно НФБК. (Хотя Дейт отмечает, что определение этой нормальной формы впервые в 1971 г. было дано Хезом (Heath)).
Отношение находится в нормальной форме Бойса-Кодда тогда и только тогда, когда детерминантыкаждой нетривиальной и неприводимой слева функциональной зависимости являются потенциальными ключами отношения.
Напомним, что детерминантом называется левая (определяющая) часть функциональной зависимости, атривиальной мы называем функциональную зависимость, у которой правая (зависимая) часть является подмножеством ее левой части (детерминанта).
То есть на диаграммах функциональных зависимостей отношения, находящегося в нормальной форме Бойса – Кодда, стрелки, указывающие на эти зависимости, должны исходить только от потенциальных ключей.
Можно обратить внимание на то, что приведенное определение нормальной формы Бойса – Кодда не использует явных ссылок на первую, вторую и третью нормальные формы, а также на транзитивнуюфункциональную зависимость, и с этой точки зрения оно концептуально проще. Однако на практике обычно более просто осуществлять нормализацию отношений путем последовательного их преобразования изпервой нормальной формы во вторую, а затем в третью нормальную форму и, если необходимо, внормальную форму Бойса – Кодда.
Рассмотрим теперь вопросы, связанные с нормальной формы Бойса – Кодда на примерах.
Пример 1.
Возвращаясь к отношению Экзамен на рис. 10.8, которое находится в первой и не находится во второйнормальной форме, можно убедиться, что отношение не находится в НФБК. Действительно, его детерминантами являются простой атрибут КОД_СТУДЕНТА и составной атрибут {КОД_СТУДЕНТА,Дисциплина}. Из этих двух детерминантов только {КОД_СТУДЕНТА, ДИСЦИПЛИНА} является потенциальным ключом отношения.
Пример 2.
Отношение студент_общежитие_АДРЕС на рис.10.12, которое находится во второй, но не находится в третьейнормальной форме, также не находится в НФБК, так как его детерминантами являются атрибутКОД_СТУДЕНТА и атрибут ОБЩЕЖИТИЕ, из которых только атрибут КОД_СТУДЕНТА является ключомотношения.
Пример 3.
Отношения СТУДЕНТЫ и УСПЕВАЕМОСТЬ, представленные на рис.10.9, и отношения СТУДЕНТ_ОБЩЕЖИТИЕ и ОБЩЕЖИТИЕ_АДРЕС на рис.10.14, которые, как мы знаем, находятся в третьей нормальной форме, также находятся и в НФБК. Действительно, их детерминанты, а именно составной атрибут {КОД_СТУДЕНТА,ДИСЦИПЛИНА} в отношении УСПЕВАЕМОСТЬ, атрибут КОД_СТУДЕНТА в отношениях СТУДЕНТЫ и СТУДЕНТ_ОБЩЕЖИТИЕ, атрибут ОБЩЕЖИТИЕ в ОБЩЕЖИТИЕ_АДРЕС, одновременно являются и ключами этих отношений.
Приведенные примеры иллюстрируют тот факт, что для отношений, в которых имеется лишь один потенциальный ключ, нахождение отношения в третьей нормальной форме эквивалентно его нахождению внормальной форме Бойса – Кодда.
Теперь рассмотрим примеры отношений, в которых больше одного потенциального ключа, а затем и примеры отношений с перекрывающимися составными потенциальными ключами.
Пример 4.
Рассмотрим отношение, диаграмма функциональных зависимостей которого имеет вид, представленный на рис. 10.16.
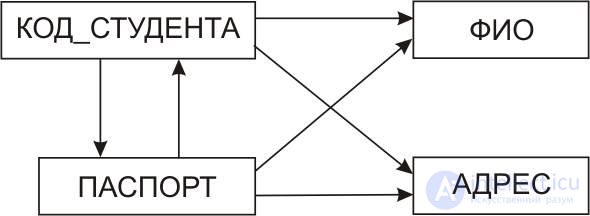
Рис.10.16. Диаграммы функциональных зависимостей отношения с двумя потенциальными ключами
Как видно из этой диаграммы, это отношение, в отличие от рассматриваемых ранее, имеет двапотенциальных ключа. Это – атрибуты КОД_СТУДЕНТА и ПАСПОРТ, от каждого из которых все остальные атрибуты зависят функционально. Это отношение находится во второй и третьей нормальных формах, так как в нем отсутствуют неприводимые слева функциональные зависимости неключевых атрибутов от потенциальных ключей и отсутствуют транзитивные зависимости.
Это отношение находится также и в нормальной форме Бойса – Кодда. Действительно, детерминанты этого отношения атрибуты КОД_СТУДЕНТА и ПАСПОРТ одновременно являются и его потенциальными ключами.
Приведенный пример иллюстрирует тот факт, что само по себе наличие в отношении нескольких потенциальных ключей не приводит к неэквивалентности третьей нормальной формы и нормальной формы Бойса – Кодда.
И, наконец, обратим внимание на следующий пример.
Пример 5.
|
Пусть в этом отношении имеют место следующие функциональные зависимости, представленные на рис. 10.18.

Рис.10.18. Диаграмма функциональных зависимостей отношения
Как видно из этих зависимостей, отношение имеет два потенциальных ключа. Ими являются составные атрибуты {КОД_СТУДЕНТА, ДИСЦИПЛИНА} и {ПАСПОРТ, ДИСЦИПЛИНА}. Обращаем внимание на то, что ключи эти являются перекрывающимися, так как атрибут Дисциплина входит в состав обоих ключей.
Представленное отношение находится в третьей нормальной форме, так как его единственный неключевой атрибут Оценка зависит от обоих ключей неприводимо, и в отношении отсутствуют транзитивные функциональные зависимости.
Однако, это отношение не находится в НФБК. Действительно, в нем имеются детерминанты КОД_СТУДЕНТА и ПАСПОРТ, которые сами не являются потенциальными ключами, хотя и входят в их состав.
Обратившись к примеру таблицы на рис.10.17, представляющей это отношение, можно увидеть наличие в нем избыточной информации: многократно повторяющиеся одинаковые пары значений атрибутов КОД_СТУДЕНТА и ПАСПОРТ. Нетрудно понять, что эта избыточность приводит к возникновению типичных аномалий операций обновления данных:
Выходом из ситуации является декомпозиция рассматриваемого отношения на два отношения.
|
|
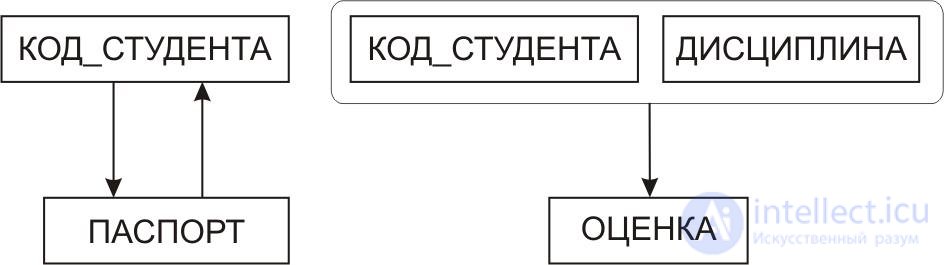
Рис.10.20. Диаграммы функциональных зависимостей отношений на рис.10.19
Возможен и другой вариант декомпозиции, представленный на рис.10.21.

Рис.10.21. Другой вариант декомпозиции отношения на рис.10.17
Можно убедиться, что каждое из отношений, представленных на рис.10.19 – 10.21, уже находится в нормальной форме Бойса – Кодда, и в них отсутствуют аномалии операций обновления данных.
Пример 6.
Пусть дано отношение со следующим набором атрибутов
{КОД_СТУДЕНТА, Дисциплина, ОЦЕНКА, НОМЕР_БИЛЕТА}.
Кортежи этого отношения представляют информацию о том, что конкретный студент при сдаче конкретной дисциплины отвечает на вопросы определенного экзаменационного билета. При этом имеется ограничение, состоящее в том, что никакие два студента не могут отвечать на один и тот же билет по одной дисциплине. Это ограничение эквивалентно следующим функциональным зависимостям
{КОД_СТУДЕНТА, ДИСЦИПЛИНА} → {НОМЕР_БИЛЕТА},
{ДИСЦИПЛИНА, НОМЕР_БИЛЕТА} → {КОД_СТУДЕНТА},
{КОД_СТУДЕНТА, ДИСЦИПЛИНА} → {ОЦЕНКА},
{ДИСЦИПЛИНА, НОМЕР_БИЛЕТА} → {ОЦЕНКА}.
Видно, что отношение имеет два перекрывающихся составных потенциальных ключа. Этими ключами являются составные атрибуты {КОД_СТУДЕНТА, ДИСЦИПЛИНА} и {ДИСЦИПЛИНА, НОМЕР_БИЛЕТА}. При этом нетрудно убедиться, что представленное отношение находится в нормальной форме Бойса – Кодда, так каквсе его детерминанты являются потенциальными ключами.
Данный пример иллюстрирует тот факт, что само по себе наличие перекрывающихся составных потенциальных ключей не является признаком того, что отношение не находится в нормальной форме Бойса – Кодда.
Рассмотренные в предыдущих разделах преобразования отношений в нормальную форму Бойса – Кодда обеспечивают полное устранение нежелательных проблем, аномалий операций обновления данных INSERT,DELETE и UPDATE, которые обусловлены наличием между атрибутами функциональных зависимостей. Для отношений, в которых имеют место только функциональные зависимости между атрибутами, приведение их к нормальной форме Бойса – Кодда заканчивает процесс их нормализации, так как в этом случае отношение уже оказывается в четвертой и пятой нормальных формах. Проблема, однако, состоит в том, что зависимости между атрибутами не исчерпываются только функциональными зависимостями. В отношениях кромефункциональных могут присутствовать и другие, более сложные, виды зависимостей между атрибутами. Так, введение рассматриваемой в данном разделе четвертой нормальной формы связано с необходимостью решения проблем, обусловленных наличием в отношении так называемой многозначной зависимости.
Рассмотрим в качестве примера отношение, представленное на рис.10.22.
|
Хорошо видно, что отношение СТУД_КУРС_ДИСЦ, приведенное на рис.10.22, страдает избыточностью и связанными с этим аномалиями операций обновления. В этом отношении между атрибутами {СТУДЕНТ, КУРС, ДИСЦИПЛИНА} существуют только тривиальные функциональные зависимости типа {СТУДЕНТ, КУРС, ДИСЦИПЛИНА}→{ДИСЦИПЛИНА} или {СТУДЕНТ, КУРС, ДИСЦИПЛИНА}→{СТУДЕНТ, КУРС} и т. д. Первичным ключом этого отношения является набор атрибутов {СТУДЕНТ, КУРС, ДИСЦИПЛИНА}, то есть весь кортежэтого отношения. Учитывая материалы предыдущих разделов, нетрудно увидеть, что это отношение уже находится в нормальной форме Бойса – Кодда, так как единственный детерминант отношения {СТУДЕНТ, КУРС, ДИСЦИПЛИНА} одновременно является его ключом. Следовательно, в этом отношении по определению должны отсутствовать проблемы, связанные с функциональной зависимостью. Однако также хорошо видно, что это отношение, тем не менее, явно страдает наличием аномалий операций обновления данных. Действительно, для добавления, например, информации о новой дисциплине на конкретном курсе мы должны добавить кортежи с этой дисциплиной для каждого студента, обучающегося на данном курсе.
Проблемы отношения, представленного на рис.10.22, связаны уже не функциональной зависимостью, а с наличием в нем так называемой многозначной зависимости, связывающей атрибут курс с атрибутами студент и дисциплина. Эта зависимость состоит в том, что конкретное значение атрибута курс однозначно определяет не одно, а множество соответствующих ему значений атрибутов студент и дисциплина, а именно множество студентов, обучающихся на данном курсе. При этом значения атрибутов студент и дисциплинадруг от друга совершенно не зависят.
Рисунок 10.23 поясняет характер зависимостей между атрибутами в данном примере, когда значения атрибута курс однозначно определяют не единичные значения атрибутов студент и дисциплина, а конкретные множества значений, а именно множество студентов, обучающихся на конкретном курсе, и множество дисциплин, изучаемых каждым студентом конкретного курса.
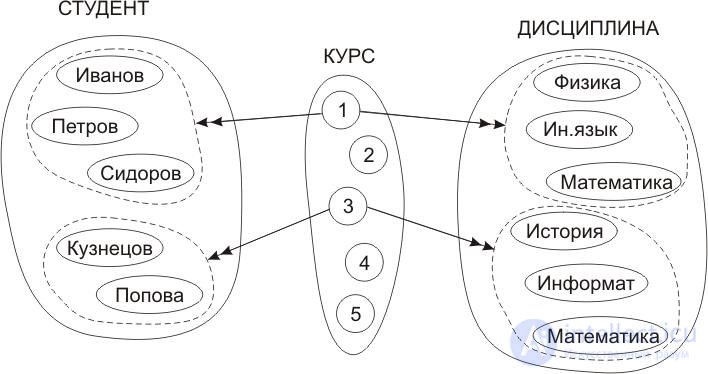
Рис.10.23. Иллюстрация многозначных зависимостей
Многозначную зависимость обозначают двойной стрелкой следующим образом:
КУРС →→ СТУДЕНТ и КУРС →→ ДИСЦИПЛИНА.
Запись А →→ В означает, что атрибут В многозначно зависит от атрибута А, или атрибут А многозначно определяет значения атрибута В.
Помещение в одну таблицу информации об элементах двух подмножеств значений атрибутов студент и дисциплина для каждого значения атрибута курс приводит к размножению кортежей отношения из-за необходимости указания всех сочетаний элементов подмножеств значений атрибутов студент и дисциплина, относящихся к конкретному значению атрибута курс.
Определение многозначной зависимости выглядит следующим образом.
Пусть А, В и С являются произвольными подмножествами множества атрибутов отношения R. Тогда В многозначно зависит от А, т. е. А →→ В, тогда и только тогда, когда множество значений В, соответствующее заданной паре {значение А, значение С} отношения R, зависит от А, но не зависит от С.
Независимость множества значений В от значений С означает, что конкретное значение А и определяемое им множество значений В может иметь место при любых значениях атрибута С.
Можно показать, что для данного отношения R{А, В, С} многозначная зависимость А →→ B выполняется тогда и только тогда, когда выполняется также зависимость А →→ С. Другими словами, многозначные зависимости в отношении всегда образуют связанные пары, и поэтому их обычно в символичном виде представляют вместе А →→ B и А →→ С, или короче – А →→ В|С.
Для рассматриваемого примера такая запись имеет следующий вид:
КУРС →→ СТУДЕНТ|ДИСЦИПЛИНА.
Если снова обратиться к рассмотренной ранее функциональной зависимости, то нетрудно увидеть, что на самом деле функциональная зависимость является частным случаем многозначной зависимости, а именно случаем, когда множество зависимых значений, соответствующих конкретным значениям детерминанта, всегда является одноэлементным множеством.
Таким образом, можно сказать, что проблемы рассматриваемого отношения (рис.10.22) связаны с тем, что оно содержит многозначные зависимости, не являющиеся функциональными.
Проблемы этого отношения решаются его декомпозицией на две проекции.
|
|
Возможность осуществления такой декомпозиции обосновывается теоремой Фейгина.
теорема фейгина .
Пусть А, В и С являются множествами атрибутов отношения R{А, В, С}. Отношение R будет равно соединению его проекций {А, В} и {А, С} тогда и только тогда, когда для отношения R выполняется многозначная зависимость А→→ В.
Можно обратить внимание на то, что теорема Фейгина является обобщением рассмотренной в разделе 10.3 теоремы Хеза, которая, напомним, звучит так.
Теорема Хеза.
Пусть R{А, В, С} является отношением, где А, В и С – атрибуты этого отношения. Если R удовлетворяет зависимости А ® В, то R равно соединению его проекций {А, В} и {А, С}.
Как видно, теорема Хеза естественным образом вытекает из теоремы Фейгина.
Теперь можно дать определение четвертой нормальной формы отношения.
Отношение R находится в четвертой нормальной форме (4НФ) тогда и только тогда, когда существуют подмножества А и В атрибутов отношения R такие, что выполняется нетривиальная многозначная зависимость А →→ В и все атрибуты R также функционально зависят от А.
Приведенное строгое определение четвертой нормальной формы требует пояснения. Последнее условие, состоящее в том, что все атрибуты отношения R также функционально зависят от А, означает, что A является потенциальным ключом отношения. В этом случае многозначная зависимость А→→ В фактически являетсявырожденной, то есть представлена в этом отношении в виде функциональной зависимости. Другими словами, нетривиальные многозначные зависимости присутствуют в отношении R только в форме K → Х, то есть атрибут Х функционально зависит от первичного ключа K.
Еще проще это определение можно сформулировать следующим образом.
Отношение R находится в четвертой нормальной форме, если оно находится в нормальной форме Бойса – Кодда, и все многозначные зависимости отношения R являются функциональными зависимостями от потенциальных ключей.
Приведенное определение четвертой нормальной формы не следует истолковывать таким образом, что при декомпозиции отношения с многозначными зависимостями именно эти зависимости становятся функциональными. Выше уже говорилось, что многозначные зависимости могут существовать только парами и при декомпозиции отношения эти пары разрываются и сами многозначные зависимости исчезают.
И, наконец, на случай наличия в отношении многозначных зависимостей может быть обобщено приведенное ранее в разделе 10.5 определение Риссанена, касающееся декомпозиции отношения на независимыепроекции. Оно имело следующий смысл.
Отношение R{А, В, С}, удовлетворяющее функциональным зависимостям А→В, следует разбивать напроекции {А, В} и {А, С}.
То же самое можно утверждать и для многозначных зависимостей А →→ В, то есть
отношение R{А, В, С}, удовлетворяющее многозначным зависимостям
А →→ В|С, следует разбивать на проекции {А, В} и {А, С}.
В предыдущих разделах, посвященных вопросам нормализации отношений, рассматриваются случаи, когда единственно необходимой и
продолжение следует...
Часть 1 Проектирование базы данных, функциональная зависимость, нормализация, нормальные формы 1НФ, 2НФ, 3НФ, 4НФ, 5НФ
Часть 2 10.6 Нормальная форма Бойса–Кодда (BCNF) - Проектирование базы данных, функциональная
Часть 3 10.9 Итоговая схема процедуры нормализации - Проектирование базы данных, функциональная
В заключение, эта статья об проектирование базы данных подчеркивает важность того что вы тут, расширяете ваше сознание, знания, навыки и умения. Надеюсь, что теперь ты понял что такое проектирование базы данных, функциональная зависимость, нормализация, нормальные формы 1нф, 2нф, 3нф, 4нф, 5нф, bcnf, теорема фейгина, теорема хеза и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Базы данных, знаний и хранилища данных. Big data, СУБД и SQL и noSQL
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Базы данных, знаний и хранилища данных. Big data, СУБД и SQL и noSQL
Термины: Базы данных, знаний и хранилища данных. Big data, СУБД и SQL и noSQL