Лекция
Сразу хочу сказать, что здесь никакой воды про понятие, и только нужная информация. Для того чтобы лучше понимать что такое понятие, абстрактная мысль , настоятельно рекомендую прочитать все из категории Логика.
Как было отмечено еще при рассмотрении первой темы данного лекционного курса, логика непосредственно интересуется не любым мышлением, а только абстрактным. Основными формами последнего являются понятие , суждение и умозаключение. Пришло время познакомиться с ними подробней.
Понятие - в логике это абстрактная мысль , выделяющая предмет как систему всех его существенных (необходимых для существования) свойств. Последняя составляет содержание понятия, а кроме содержания у него есть объем - предмет, соответствующий содержанию.
Понятие в психологии— отображенное в мышлении единство существенных свойств и отношений предметов; мысль, выделяющая и обобщающая предметы некоторого класса по общим и в своей совокупности специфическим для них признакам. В уточненной формулировке: понятие есть мысль, которая посредством указания на некоторый признак выделяет из универсума и собирает (обобщает) предметы, обладающие этим признаком
Понятие в его отвлеченности противостоит конкретности восприятия. Также понятие противостоит слову, которое можно трактовать как знак понятия
Слова и словосочетания, обозначающие понятия, называются терминами
Роль объема может играть какой-то единичный предмет, и тогда понятие называется единичным (например, понятие Земли), или же произвольный элемент множества, и тогда понятие называется общим (например, понятие планеты). Для единичного понятия графическим изображением объема служит точка, для общего - круг, каждая точка которого означает элемент данного множества.
В формализованном представлении в самом общем виде любое понятие выражается следующей языковой конструкцией :
,
где - целое число,
- (упорядоченный) кортеж предметов длиной
из декартового произведения
такой, что для предметов
выполняется отношение
. Называется эта конструкция универсалией. В случае, когда
понятие выражается универсалией вида:
,
где предметы принадлежат универсуму
и обладают признаком
.
В русских философских словарях XVIII века (см. Антиох Кантемир и Григорий Теплов) термин «понятие» сближался с «идеей».
Под понятием Кант разумел любое общее представление, поскольку последнее фиксировано термином. Отсюда и его определение: «Понятие… есть общее представление или представление того, что обще многим объектам, следовательно — представление, имеющее возможность содержаться в различных объектах».
Понятие для Гегеля — «прежде всего синоним действительного понимания существа дела, а не просто выражение любого общего, любой одинаковости объектов созерцания. В понятии раскрывается подлинная природа вещи, а не ее сходство с другими вещами, и в нем должна поэтому находить свое выражение не только абстрактная общность (это лишь один момент понятия, роднящий его с представлением), а и особенность его объекта. Вот почему формой понятия оказывается диалектическое единство всеобщности и особенности, которое и раскрывается через разнообразные формы суждения и заключения, а в суждении выступает наружу. Об этом говорит сайт https://intellect.icu . Неудивительно, что любое суждение ломает форму абстрактного тождества, представляет собою ее самоочевиднейшее отрицание. Его форма — А есть В (то есть не‑A)» .
Всеобщее понятие выражает не простую абстрактную общность, одинаковость единичных представителей данного класса, но «действительный закон возникновения, развития и исчезновения единичных вещей» .
Понятия суть «сокращения, в которых мы охватываем, сообразно их общим свойствам, множество различных чувственно воспринимаемых вещей» (Ф. Энгельс) .
Содержание и объем понятия связаны законом обратного отношения: с увеличением содержания (объема) уменьшается объем (содержание). Покажем действие этого закона на примере. Возьмем понятие "лес". Его содержание можно передать так: "массив дикорастущих деревьев". Здесь в кавычках системно указаны все существенные свойства любого леса. Уменьшим это содержание, удалив свойство "дикорастущий". Получилось понятие "массив деревьев", объем которого помимо лесов составляют парки и сады. Следовательно, исходный объем увеличился. Теперь увеличим исходное содержание, добавив свойство "лиственный". Так вместо понятия "лес" мы получим понятие "лиственный лес". Сравнив объемы этих понятий, легко увидеть, что у второго объем меньше, чем у первого.
Демонстрируя действие закона обратного отношения между содержанием и объемом понятия, мы провели обобщение и ограничение понятия "лес". Обобщение (ограничение) понятия - это логическая операция по увеличению (уменьшению) объема исходного понятия.
Рассмотрим основные способы обобщения понятий. При этом символическая запись последних будет напоминать формулы из языка логики предикатов. Так, понятие А будет иметь вид х А (х) (читается: "х такой, что А от х"), где х в общем случае обозначает произвольный предмет, а А - какой-то признак.
Основные способы обобщения понятий
| Название способа | Схема | Пример |
| Традиционный (по закону обратного отношения между содержанием и объемом) | x(A(x)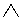 B (x)) B (x)) xА (х) xА (х) |
"студент-отличник"  "студент" |
| Дизъюнктивный | хА(х)  x (A (x) x (A (x)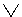 B (x)) B (x)) |
"студент"  "студент или школьник" "студент или школьник" |
| Введение существования | хА(х,a) x x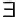 yA (x,y) yA (x,y) |
"студент, знающий астрономию"  "студент, знающий какую-то науку" "студент, знающий какую-то науку" |
| Удаление всеобщности | х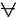 yА(х,y) yА(х,y) хА (х,a) хА (х,a) |
"студент, знающий любую науку"  "студент, знающий астрономию" "студент, знающий астрономию" |
От способов обобщения легко перейти к способам ограничения, если в приведенной таблице все стрелки повернуть в обратную сторону. При этом три последних способа будут называться "удаление дизъюнкции", "удаление существования" и "введение всеобщности".
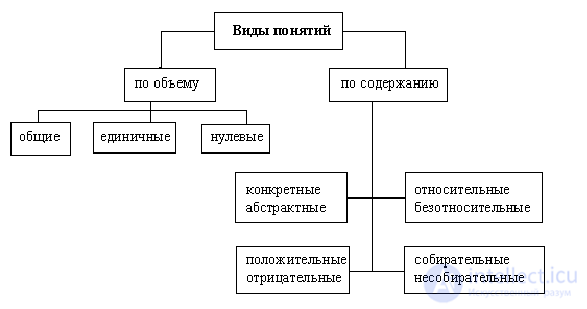
Классификацию понятий обычно проводят по отношениям между их объемами. Сначала выделяют совместимые и несовместимые понятия: в объемах первых есть хотя бы один общий элемент, в объемах вторых общие элементы отсутствуют. Затем два эти типа делят на виды - по характеру совместимости или несовместимости.
Виды совместимых понятий: равнозначные (разные содержания, но одинаковый объем), перекрещивающиеся (объемы частично совпадают) и субординационные (Объем одного из понятий полностью включается в объем другого, не исчерпывая последний. При этом первое понятие называют подчиненным второму, а второе - подчиняющим себе первое).
Виды несовместимых понятий: соподчиненные (несовместимые понятия, подчиненные одному и тому же понятию), контрарные, или противоположные (несовместимые понятия, объемы которых располагаются на полюсах объема подчиняющего понятия) и контрадикторные, или противоречащие друг другу (несовместимые понятия, объемы которых вместе составляют объем подчиняющего понятия). Представим эту информацию в виде таблицы, дополнив ее круговыми схемами и примерами:
Понятия
| Совместимые | Несовместимые |
Равнозначные (пример: "равносторонний прямоугольник" и "равноугольный ромб")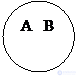 |
Соподчиненные (пример: "грач" и "галка")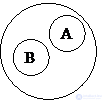 |
Перекрещивающиеся (пример: "студент" и "отличник")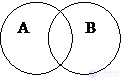 |
Контрарные, или противоположные ("молчун" и "болтун")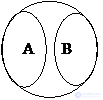 |
Субординационные (пример: "животное" и "птица")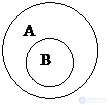 |
Контрадикторные, или противоречащие друг другу (пример: "молчун" и "немолчун")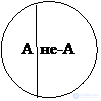 |
Помимо обобщения и ограничения понятия основными логическими операциями с ним являются определение и деление.
Определение понятия - это логическая операция, в ходе которой раскрывается содержание понятия. Таким образом, определить понятие значит раскрыть его содержание, т.е. системно сформулировать все основные свойства соответствующего понятию предмета.
От определения понятия следует отличать приемы, сходные с ним. Рассмотрим основные из этих приемов.
1. Остенсивное определение - это демонстрация (показ) предмета. Простой пример: остенсивно определить Луну можно, указав на нее пальцем. Остенсивным определением считается и использование для объяснения собственных имен. Например, если нужно остенсивно определить, что такое планета нашей солнечной системы, легче всего сделать это, назвав каждую из определяемых планет по имени.
2. Сравнение - это указание сходства или различия одного предмета по отношению к другому. Пример: закат похож на восход.
3. Разъяснение через пример - это приведение примера, иллюстрирующего данное понятие. Иллюстрацией понятия является его чувственный образ. Пример: гениальный полководец - это Суворов.
4. Описание, т.е. перечисление всех известных свойств предмета.
5. Характеристика - это указание существенных в некотором отношении свойств предмета. Характеристика ближе всего к определению понятия, но и она не может заменить последнее, так как, определяя понятие, указывают существенные вообще, а не в каком-то конкретном отношении свойства предмета.
Определения понятий делят на номинальные и реальные. Номинальным называют определение понятия на основе соглашения (конвенции). Конвенциональный характер такого определения находит свое отражение в соответствующих оговорках. Например: "Под новым русским мы будем понимать современного российского бизнесмена". Выражение "мы будем понимать" говорит о том, что уже есть или должна появиться группа лиц, принимающих данное определение. Как правило, понятие определяют номинально, когда нет уверенности, что в ходе этой операции его содержание действительно будет раскрыто. Таким образом, номинальное определение имеет субъективный характер. Другое дело - реальное определение. Оно дает объективное знание, так как действительно раскрывает содержание понятия. Поэтому здесь нет места для оговорок.
По завершенности определения делят на явные и неявные. Явное - это завершенное, не требующее доработки определение. Неявное определение, напротив, требует доработки. Одним из его видов является определение через отношение к противоположному. Возьмем пример: "Самец - это животное, противоположное по полу самке". Здесь нужны дополнительные разъяснения, так как понятие самца определено через противоположное ему понятие самки, а всякое понятие, противоположное данному, того же уровня сложности, что и данное.
Другой вид неявного определения - определение через контекст. Это тот случай, когда текст содержит все необходимые для определения понятия слова, но они разбросаны по разным предложениям, и нужно свести их в одну фразу, чтобы получилось явное определение.
Рассмотрим основные правила определения понятия.
1. Определяемое и определяющее понятия должны быть равнозначными. Пример: "Грузовик - это автомобиль для перевозки грузов". Здесь определяемое понятие "грузовик" равнозначно определяющему понятию "автомобиль для перевозки грузов". Следовательно, первое правило определения не нарушено. При его нарушении различают четыре ошибки:
1) Широкое определение (определяющее понятие подчиняет себе определяемое). Пример: "Дуб - это лиственное дерево".
2) Узкое определение (определяемое понятие подчиняет себе определяющее). Пример: "Студент - это учащийся университета".
3) Перекрещивание. Пример: "Нож - это холодное оружие". Здесь перекрещивание понятий, потому что, с одной стороны, нож не обязательно оружие, а с другой - холодное оружие не обязательно нож.
4) Определение как попало (определяющее понятие несовместимо с определяемым). Пример: "Человек - это биоробот, созданный инопланетным разумом".
2. Определение не должно содержать круга, т.е., определяя данное понятие, нельзя его же и использовать. Часто круг возникает, когда злоупотребляют однокорневыми словами. Пример: "Логика - это знание о логическом мышлении". Здесь прилагательное "логический", использованное при записи определяющего понятия, возвращает к однокорневому слову "логика", которым выражено определяемое понятие.
3. Определение должно быть ясным, т.е. не должно требовать дополнительных разъяснений. К нарушению этого правила приводит, во-первых, злоупотребление новыми словами (часто - иностранного происхождения, что характерно для современной научной литературы)), а во-вторых - применение обычных выражений в необычном смысле.
4. Номинальное определение нельзя выдавать за реальное.
Теперь от определения понятия перейдем к его делению. Деление понятия - это логическая операция, в ходе которой с помощью какого-то признака (основания деления) объем исходного понятия раскладывается на ряд элементов, соответствующих понятиям-членам деления.
Различают мереологический и таксономический типы деления. Мереологическим называется деление единичного понятия по принципу "единичное целое - части". Пример: "Рука делится на кисть, плечо и предплечье". Таксономическим является деление общего понятия по принципу "множество - подмножества". Пример: "Рука бывает умелой и неумелой". В этих примерах деления следует обратить внимание на то, что одним и тем же выражением языка могут обозначаться разные понятия: в одном случае - единичное, а в другом - общее.
1. Деление должно быть соразмерным, т.е. объединение членов деления должно составить делимое понятие. При нарушении соразмерности получаются ошибки двух видов:
1) Деление с лишними членами (лишним членом). Пример: "Угол бывает нулевым, острым, прямым и тупым". Здесь первый член деления лишний, так как нулевой угол в отличие от остальных является вырожденным.
2) Неполное деление. Пример: "Углы бывают острыми и тупыми".
2. Деление должно проводиться только по одному основанию. Ошибка: сбивчивое деление. Пример: "Углы бывают острыми, прямыми, тупыми и закругленными".
3. Члены деления должны исключать друг друга.
4. Деление должно быть непрерывным, т.е. его следует проводить только на одном уровне. Ошибка: скачок в делении. Пример: "Углы бывают острыми, прямыми, тупыми и развернутыми". Здесь смешаны два уровня деления: сначала нужно было делить углы на неразвернутые и развернутые, а уже потом неразвернутые - на три указанных вида.
Когда, проведя деление понятия, переходят к делению членов деления, получается классификация, т.е. система последовательно осуществляемых делений. Простейшая классификация - двухуровневая.
Основные черты правильной классификации:
1. Все основания деления подчинены решению единой задачи.
2. Члены классификации разбиты на группы так, что по месту в классификации легко судить о содержании членов классификации.
3. Содержание классификации представлено или может быть представлено в виде таблицы или схемы.

Вот что получается, когда понятие "автопилот" определяют через понятие "тот, кто сам себя пилотирует"
Пожалуйста, пиши комментарии, если ты обнаружил что-то неправильное или если ты желаешь поделиться дополнительной информацией про понятие Надеюсь, что теперь ты понял что такое понятие, абстрактная мысль и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Логика
Комментарии
Оставить комментарий
Логика
Термины: Логика