Округление чисел

Привет, мой друг, тебе интересно узнать все про округление чисел, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое округление чисел , настоятельно рекомендую прочитать все из категории Арифметика.

Числа округляют, когда полная точность не нужна или невозможна.

Натуральные числа округляют до десятков, сотен, тысяч и т.д. Названия цифр в разрядах натурального числа можно вспомнить в теменатуральные числа.

В зависимости от того, до какого разряда надо округлить число, мы заменяем нулями цифру в разрядах единиц, десятков и т.д.

Если число округляется до десятков, то нулями заменяем цифру в разряде единицы.

Если число округляется до сотен, то цифра ноль должна стоять и в разряде единиц, и в разряде десятков.

Записывают результат округления после специального знака «≈». Этот знак читается как «приближенно равно».

При округлении натурального числа до какого-либо разряда надо воспользоваться правилами округления.

1. Подчеркнуть цифру разряда, до которого надо округлить число.
2. Отделить все цифры, стоящие справа этого разряда вертикальной чертой.
3. • Если справа от подчеркнутой цифры стоит цифра 0, 1, 2, 3 или 4, то все цифры, которые отделены справа, заменяются нулями. Об этом говорит сайт https://intellect.icu . Цифру разряда, до которой округляли, оставляем без изменений.
   • Если справа от подчеркнутой цифры стоит цифра 5, 6, 7, 8 или 9, то все цифры, которые отделены справа, заменяются нулями, а к цифре разряда, до которой округляли, прибавляется 1.

Поясним на примере. Округлим 57 861 до тысяч. Выполним первые два пункта из правил округления.

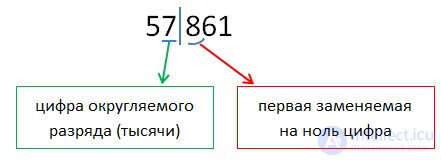
После подчеркнутой цифры стоит цифра 8, значит к цифре разряда тысяч (у нас это 7) прибавим 1, а все цифры, отделенные вертикальной чертой заменим нулями.

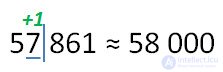
Теперь округлим 756 485 до сотен.

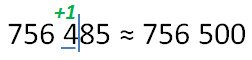
Округлим 364 до десятков.

36|4 ≈ 360 - в разряде единиц стоит 4, поэтому мы оставляем 6 в разряде десятков без изменений.

На числовой оси число 364 заключено между двумя «круглыми» числами 360 и 370. Эти два числа называют приближенными значениями числа 364 с точностью до десятков.

Число 360 - приближенное значение с недостатком, а число 370 - приближенное значение с избытком.

В нашем случае, округлив 364 до десятков, мы получили, 360 - приближенное значение с недостатком.

Округленные результаты часто записывают без нулей, добавляя сокращения «тыс.» (тысяча), «млн.» (миллион) и «млрд.» (миллиард).

Примеры:

• 8 659 000 = 8 659 тыс.
• 3 000 000 = 3 млн.

Округление также применяется для прикидочной проверки ответа в вычислениях.

Пусть нам нужно посчитать:

794 • 52 = 

До точного вычисления сделаем прикидку ответа, округлив множители до наивысшего разряда.

794 • 52 ≈ 800 • 50 ≈ 40 000

Делаем вывод, что ответ будет близок к 40 000.

794 • 52 = 41 228

Аналогично можно выполнять прикидку округлением и при делении чисел.

Если я не полностью рассказал про округление чисел? Напиши в комментариях Надеюсь, что теперь ты понял что такое округление чисел и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Арифметика

Из статьи мы узнали кратко, но содержательно про округление чисел