Алгоритм Крускала сущность,оценка сложности, области применения кратко

Привет, сегодня поговорим про алгоритм крускала, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое алгоритм крускала , настоятельно рекомендую прочитать все из категории Алгоритмы и теория алгоритмов.

алгоритм крускала — алгоритм построения минимального остовного дерева взвешенного связного неориентированного графа. Алгоритм впервые описан Джозефом Крускалом в 1956 году.

Алгоритм Крускала находит безопасное ребро для добавления в растущий лес путем поиска ребра (u, v) с минимальным весом среди всех ребер, соединяющих два дерева в лесу. Обозначим два дерева, соединяемые ребром (u, v), как С1 и С2. (u, v) — безопасное для С1 ребро. Алгоритм Крускала является жадным, поскольку на каждом шаге он добавляет к лесу ребро с минимальн возможным весом.

Реализация алгоритма Крускала напоминает алгоритм для вычисления связных компонентов. Она использует структуру для представления непересекающихся множеств. Каждое множество содержит вершины дерева в текущем лесу. Операция Find_Set(u) возвращает представительный элемент множества, содержащего u. Таким образом, мы можем определить, принадлежат ли две вершины u и v одному и тому же дереву, проверяя равенство FindJSet(u) и Find_Set(v). Объединение деревьев выполняется при помощи процедуры Union.

Алгоритм Крускала (или алгоритм Краскала) — эффективный алгоритм построенияминимального остовного дерева взвешенного связного неориентированного графа. Также алгоритм используется для нахождения некоторых приближений для задачи Штейнера . Алгоритм впервые описан Джозефом Крускалом (англ.) в 1956 году.

Формулировка

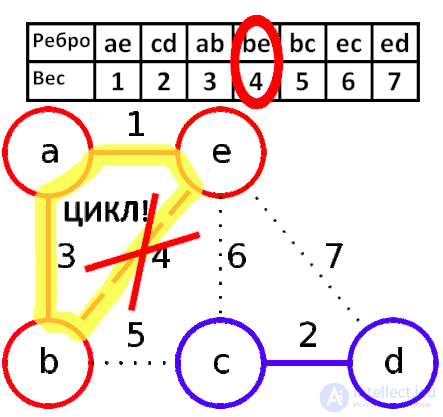
Вначале текущее множество ребер устанавливается пустым. Затем, пока это возможно, проводится следующая операция: из всех ребер, добавление которых к уже имеющемуся множеству не вызовет появление в нем цикла, выбирается ребро минимального веса и добавляется к уже имеющемуся множеству. Когда таких ребер больше нет, алгоритм завершен. Подграф данного графа, содержащий все его вершины и найденное множество ребер, является его остовным деревом минимального веса. Подробное описание алгоритма можно найти в литературе .

Формальное описание

MST_Kruskal(G,w)
1    A «- пустое множество
2    for (Для) каждой вершины v є V[G]
3            do Make_Set(v)
4    Сортируем ребра из Е в неубывающем порядке их весов w
5    for (Для) каждого (u, v) G Е (в порядке возрастания веса)
6            do if Find_Set(u) != Find_Set(v)
7                     then A «- A объеденить с {(u, v)}
8                             Union(u, v)
9    return A

В строках 1-3 выполняется инициализация множества А пустым множеством и создается |V| деревьев, каждое из которых содержит по одной вершине. Ребра в Е в строке 4 сортируются согласно их весу в неубывающем порядке. Цикл for в строках 5-8 проверяет для каждого ребра (u, v), принадлежат ли его концы одному и тому же дереву. Если это так, то данное ребро не может быть добавлено к лесу без того, чтобы создать при этом цикл, поэтому в таком случае ребро отбрасывается. В противном случае, когда концы ребра принадлежат разным деревьям, в строке 7 ребро (и, у) добавляется в множество А, и вершины двух деревьев объединяются в строке 8.

Оценка сложности

Время работы алгоритма Крускала для графа G = (V, Е) зависит от реализации структуры данных для непересекающихся множеств. Об этом говорит сайт https://intellect.icu . Будем считать, что лес непересекающихся множеств реализован с эвристиками объединения по рангу и сжатия пути, поскольку асимптотически это наиболее быстрая известная реализация. Инициализация множества А в строке 1 занимает время О (1), а время, необходимое для сортировки множества в строке 4, равно О (E*lgE) (стоимость |V| операций Make_Set в цикле for в строках 2-3 учитывается позже). Цикл for в строках 5-8 выполняет О (Е) операций Find_Set и Union над лесом непересекающихся множеств. Вместе с |V| операциями Make_Set эта работа требует времени О ((V + Е) * a(V)), где а — очень медленно растущая функция. Поскольку мы предполагаем, что G — связный граф, справедливо соотношение |E| >= |V| - 1, так что операции над непересекающимися множествами требуют О (Е *а(V)) времени. Кроме того, поскольку a(|V|) = О(lgV) = O(lgE), общее время работы алгоритма Крускала равно О (E*lgE). Заметим, что |Е| < |V|2, поэтому lg |E| = О (lg V) и время работы алгоритма Крускала можно записать как О (Е * lg V).

До начала работы алгоритма необходимо отсортировать ребра по весу, это требует O(E × log(E)) времени. После чего компоненты связности удобно хранить в видесистемы непересекающихся множеств. Все операции в таком случае займут O(E × α(E, V)), где α — функция, обратная к функции Аккермана. Поскольку для любых практических задач α(E, V) < 5, то можно принять ее за константу, таким образом, общее время работы алгоритма Крускала можно принять за O(E * log(E)).

Доказательство корректности алгоритма

Алгоритм Крускала действительно находит остовное дерево минимального веса, поскольку он является частным случаем алгоритма Радо — Эдмондса для графического матроида, где независимые множества — ациклические множества ребер.

Пример Выполнения алгоритма Крускала:

1. Начальная фаза. Минимальный покрывающий лес пуст.

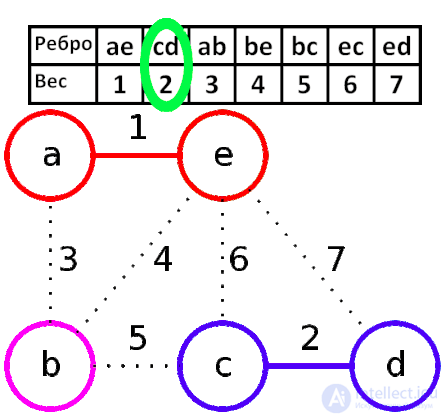
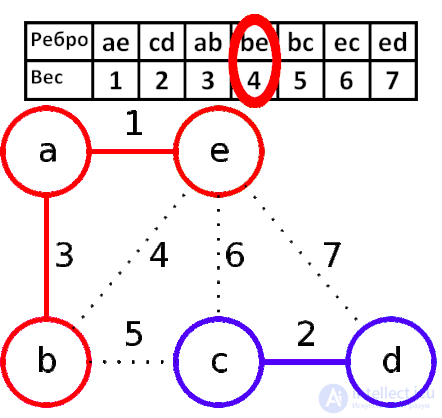
2. Перебираем ребра в порядке возрастания веса: первое ребро с весом 2. Добавляем его к А.

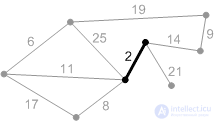
3. Следующее безопасное ребро с весом 6. Добавляем его.

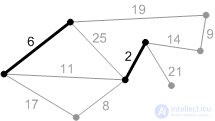
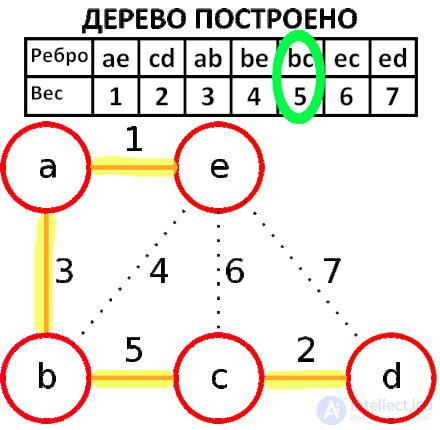
4-8. Добавляем остальные безопасные ребра.

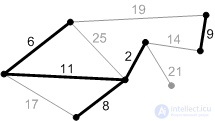
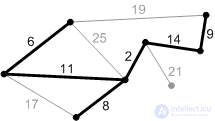
Ребра с весом 17, 19 и 25 – не безопасные. Их концы лежат в одной компоненте связности. Ребро с весом 21 – безопасное, поэтому добавляем его. Минимальное остовное дерево построено

Пример 2

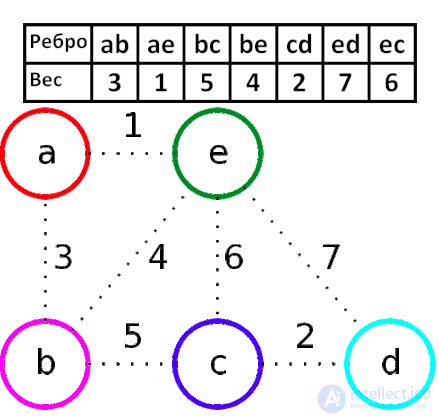
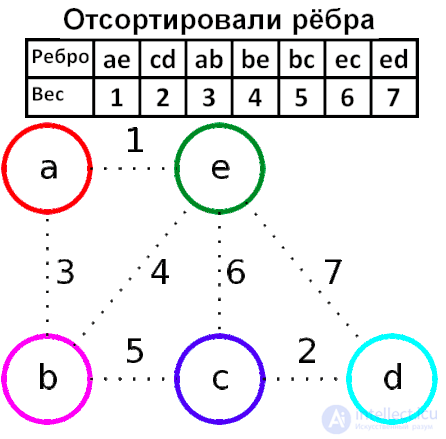
1. отсортировать весы ребер

2. выбираем минимально которое не образовывает циклов

Пример 3

Изображение	Описание
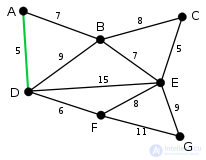	Ребра AD и CE имеют минимальный вес, равный 5. Произвольно выбирается ребро AD (выделено на рисунке).
	Теперь наименьший вес, равный 5, имеет ребро CE. Так как добавление CE не образует цикла, то выбираем его в качестве второго ребра.
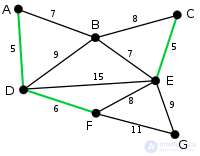	Аналогично выбираем ребро DF, вес которого равен 6.
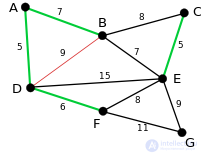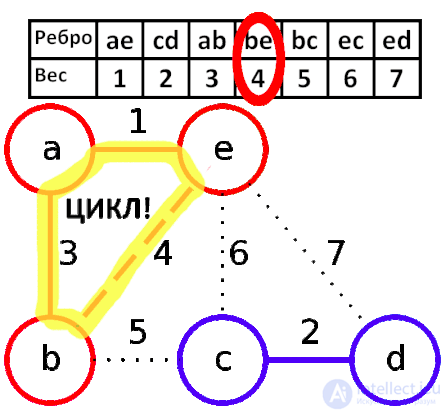
	Следующие ребра — AB и BE с весом 7. Произвольно выбирается ребро AB, выделенное на рисунке. Ребро BD выделено красным, так как уже существует путь (зеленый) между A и D, поэтому, если бы это ребро было выбрано, то образовался бы цикл ABD.
	Аналогичным образом выбирается ребро BE, вес которого равен 7. На этом этапе красным выделено гораздо больше ребер: BC, потому что оно создаст цикл BCE, DE, потому что оно создаст цикл DEBA, и FE, потому что оно сформирует цикл FEBAD.
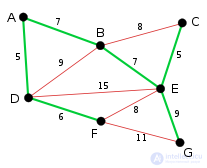	Алгоритм завершается добавлением ребра EG с весом 9. Минимальное остовное дерево построено.

Применение алгоритма, Области применения

• Разработка сетей. например соединении n городов в единую телефонную сеть с минимальной суммарной стоимостью соединений.
• Производство печатных плат. По аналогии с сетью: мы хотим соединить n контактов проводами с минимальной суммарной стоимостью. (Здесь стоит отметить, что задача о минимальном остовном дереве является упрощением реальности. В самом деле, если соединяемые контакты находятся в вершинах единичного квадрата, разрешается соединять любые его вершины, и вес соединения равен его длине, то минимальное покрывающее дерево будет состоять из трех сторон квадрата. Между тем все его четыре вершины можно электрически соединить двумя пересекающимися диагоналями, суммарная длина которых будет равна 2√2, что меньше 3 в первом случае).
• Минимальное остовное дерево может использоваться для визуализации многоаспектных, многомерных данных, например, для отображения их взаимосвязи (на картинке ниже продемонстрировано дерево схожести различных животных видов по размеру костей).
• Наука, и в частности биология, используют многомерные данные для группировки объектов, растений, животных. Минимальное остовное дерево позволяет разбивать их на взаимосвязанные классы, четко отслеживая близкие по строению и характеристикам группы.

Вопросы для самопроверки:

• 1. Что называется весом или длиной дуги?
• 2. Дайте определение остов графа.
• 3. Дайте определение минимальный остов графа.
• 4. В чем смысл алгоритма Краскала?
• 5. Перечислите области применения алгоритма Краскала.

Вау!! 😲 Ты еще не читал? Это зря!

• Остовное дерево
• Алгоритм Борувки
• Алгоритм Прима
• Алгоритм Дейкстры
• Алгоритм обратного удаления
• Односвязная кластеризация
• Жадный геометрический гаечный ключ

На этом все! Теперь вы знаете все про алгоритм крускала, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое алгоритм крускала и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Алгоритмы и теория алгоритмов

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.