Лекция
Теории систем с запаздыванием изучают системы, где отклик на входной сигнал не происходит мгновенно, а с некоторой задержкой (запаздыванием). Запаздывание – это временной промежуток, который возникает между воздействием на систему и ее реакцией на это воздействие. Такие системы важны в прикладных науках и технике, так как запаздывание часто присутствует в реальных процессах — от передачи данных в сети до химических реакций, биологических процессов и экономических моделей.
Теория систем с запаздыванием изучает поведение и управление системами, в которых реакция на воздействие происходит с временной задержкой. В таких системах отклик на входной сигнал (например, изменение температуры, подача напряжения или введение экономической меры) наступает не мгновенно, а спустя определенный промежуток времени. Это свойство широко распространено в реальных процессах и характерно для различных областей, таких как инженерия, экономика, биология и химия.Запаздывание в системах может иметь серьезные последствия: оно усложняет поведение системы, влияет на устойчивость и может вызывать нежелательные колебания и затяжные переходные процессы. Основные задачи теории систем с запаздыванием включают анализ устойчивости, моделирование переходных процессов и разработку методов управления, которые учитывают влияние временной задержки. Для математического описания таких систем используются дифференциальные уравнения с запаздыванием, методы частотного анализа, а также специализированные алгоритмы управления, такие как предсказатель Смита. Теория систем с запаздыванием помогает создать модели, максимально приближенные к реальности, и разрабатывать алгоритмы, которые позволяют компенсировать задержки, делая управление более точным и эффективным.
Типы запаздываний:
Математические модели:
Линейной системой с запаздыванием называется такая, которая содержит в своей структуре хотябы одно звено, в котором есть неизменное запаздывание во времени τ изменения выходной координаты после начала изменения входной.
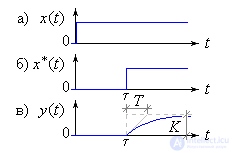
Рассмотрим апериодическое звено первого порядка, которое описывается уравнением:
T·dy/dt+y=K·x(t).(1)
Уравнение соответствующего звена с запаздыванием τ будет иметь вид:
T·dy/dt+y=K·x(t−τ). (2)
Оно называется дифференциально-разностным.
Обозначим x*(t)=x(t−τ), тогда уравнение (2) запишется в обыкновенном виде:
T·dy/dt+y=K·x*(t). (3)
Следовательно его переходная характеристика соответствует апериодическому звену (рис. 1в), но задержана на τ с, что определено задержкой воздействия x*(t) (рис. 1б).
Резюме:
Рабочие файлы: [e^(-st)_tc.vsm]

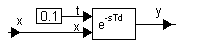
Свойства звена таковы, что y(t)=x(t−τ), где τ – запаздывание, а x(t−τ)=0 при 0
Разложим правую часть уравнения (т.е. выходной сигнал) в ряд Тейлора:
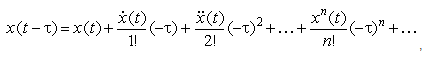 ,
,
или
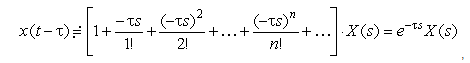 ,
,
т.е.:
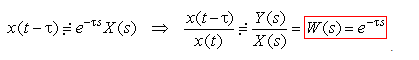 .
.
1 Сравним переходные функции апериодического звена с запаздывающим аргументом и апериодического звена 2-ого порядка:
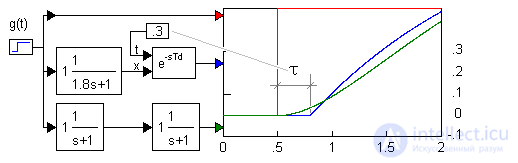
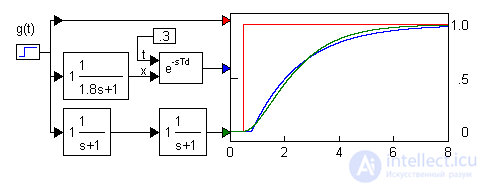
Поскольку они существенно похожи, в приближенных расчетах можно осуществлять подмены передаточных функций звеньев.
2 В некоторых случаях применяется прием учета большого числа N звеньев в системе с малыми постоянными времени ΔTi и единичным коэффициентом передачи, одним звеном с постоянным запаздыванием, равным сумме этих постоянных времени τ=∑ΔTi≈N·ΔT. Т.е.:
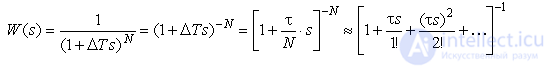
Если N→∞, то в пределе получим W(s)≈e−τs. Уже при N=8÷10 степень приближения высока. Ряд будет более точно соответствовать разложению в ряд функции e−τs, если его представлять не апериодическими, а фазосдвигающими звеньями.
Большинство методов исследования устойчивости или качества систем в качестве входной информации используют ПФ системы для разомкнутого состояния W(s). Звено чистого запаздывания является нелинейным элементом, и затрудняет как аналитический анализ систем, так и машинный (программы математического моделирования не могут выполнять функции анализа для систем с нелинейными элементами). Поэтому либо используют линеаризованные аппроксиматоры звена чистого запаздывания, либо размыкают систему в той ветви, которая содержит звено чистого запаздывания, дабы ПФ имела вид: W(s)=Wо(s)×e−τs, где Wо(s) – ПФ части системы без запаздывания.
Рассмотрим и разомкнем системы с основными вариантами включения звена чистого запаздывания – последовательным, параллельным и в цепи ОС:
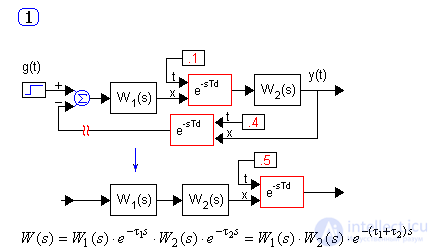
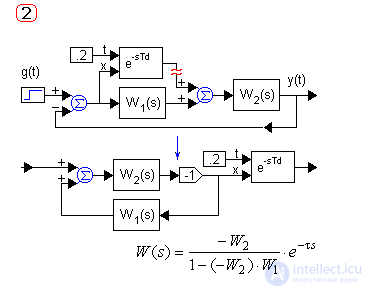
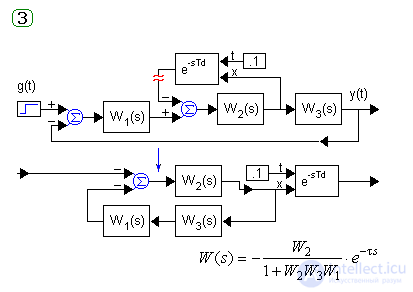
Если звенья чистого запаздывания имеются в разных ветвях структурной схемы, то для исследований используют их аппроксиматоры и машинные методы анализа.
Рабочие файлы: [ЧХ звена запаздывания]
Перейдем в частотный домен:
W(jω)=Wо(jω)×e−jωτ=Aо(ω)·ejφо(ω)×1e−jωτ,
следовательно:
L(ω)=|W(jω)|=Aо(ω)×1=Aо(ω),
φ(ω)=φо(ω)−ωτ.
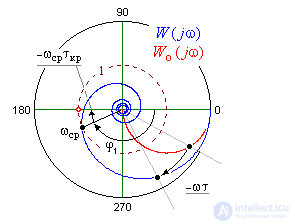
Резюме:
Запаздывания могут существенно повлиять на устойчивость системы. Даже в простых системах с постоянным запаздыванием могут возникнуть колебательные или хаотические режимы, которые невозможно описать при отсутствии запаздывания. Методы устойчивости, такие как критерий устойчивости Ляпунова–Красовского, используются для оценки влияния запаздывания на поведение системы.
Рассмотрим замкнутую систему:
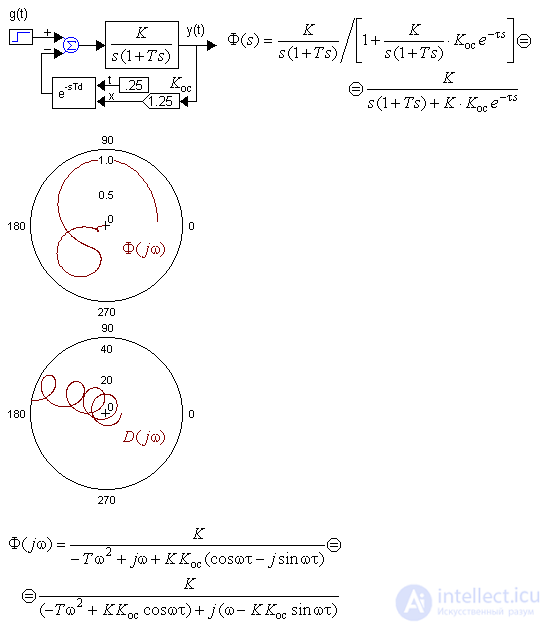
По знаменателю ПФ Φ(jω) видно, что в общем случае характеристическое уравнение будет иметь множитель e−τs, который определяет возможность наличия бесконечного количества корней (см. петли годографа Михайлова D(jω)).
Как и прежде, для устойчивости все они должны иметь отрицательные вещественные части.
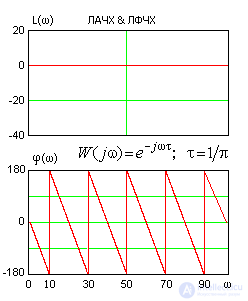
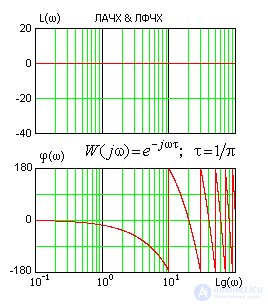
По ЧХ звена чистого запаздывания наглядно видно, что его коэффициент передачи во всем частотном диапазоне равен единице. Причем в области низких частот и задержка в звене пренебрежимо мала (т.е. сдвиг фазы стремится к нулю), поэтому при исследовании точности систем с запаздыванием допустимо просто исключить все звенья чистого запаздывания из структурной схемы. Эта операция допустима, поскольку точность любой системы определяет только НЧ часть ее ЧХ.
Типичным является, так называемое, транспортное запаздывание. Например, процесс обработки материала связан с транспортированием его от одного агрегата к другому, к примеру, от ванны окраски текстильной ткани к сушильным барабанам.
На транспортировку затрачивается время τ.
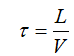 (1)
(1)
где: L - расстояние между агрегатами, V - скорость транспортировки.
При описании такого двухагрегатного объекта регулирования затрачиваемое на транспортировку время представляется в виде звена чистого запаздывания.
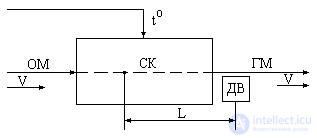
Другим типичным примером является запаздывание в канале обратной связи, вызванное невозможностью установки датчика непосредственно в зоне обработки материала.
Звено запаздывания применяется также для упрощенного описания объектов управления с распределенными параметрами, для уменьшения порядка передаточной функции и т.д.
Звено чистого запаздывания описывается уравнением
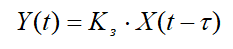 (2)
(2)
При 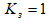 передаточная функция звена имеет вид:
передаточная функция звена имеет вид:
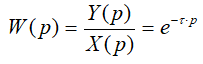 (3)
(3)
Исследование устойчивости САУ с чистым запаздыванием
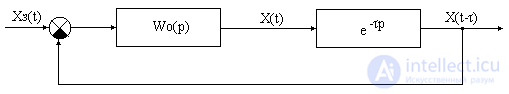
Наиболее удобным для исследования рассматриваемых систем является критерий устойчивости Найквиста. Структурная схема САУ будет иметь вид, представленный на рис.1, где Wo(p) – передаточная функция, включающая в себя объект, силовой преобразователь, датчик и регулятор.
Частотная передаточная функция разомкнутой системы будет иметь вид:
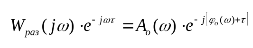 (4)
(4)
где: Ао(ω) и φo(ω) - амплитудно-частотная и фазо-частотная характеристики объекта управления без запаздывания.
При прохождении АФЧХ через эту точку справедлива следующая система уравнений
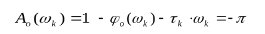
где:ωk- критическое значение частоты, τk- критическая величина запаздывания.
Или
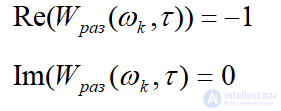
Величина τk определяется следующим образом. Из первого уравнения системы (5) определяется k, а из второго k.
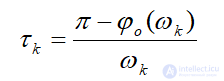 (7)
(7)
Очевидно, что для нормальной работы замкнутой САУ необходимо, чтобы величина запаздывания была
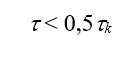 (8).
(8).
Приближенное описание звена с чистым запаздыванием
При исследовании аналитическими методами САУ с запаздыванием применение описания передаточной функцией (3) приводит к трансцендентным уравнениям. Поэтому наряду с точным описанием звена чистого запаздывания применяются приближенные рациональные передаточные функции.
Одно из таких приближений базируется на использовании ряда Тейлора
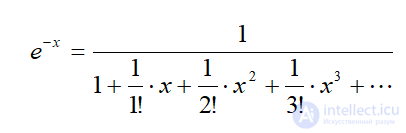
Следовательно, выражение (3) может быть приблизительно представлено звеном первого порядка
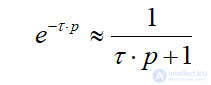 (9)
(9)
или звеном второго порядка
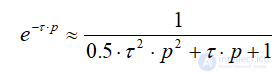 (10)
(10)
и т.д.
Более точное приближение дает разложение в ряд Паде. При использовании звена первого порядка
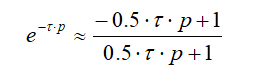 (11)
(11)
При использовании звена второго порядка
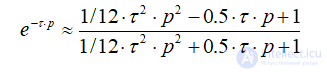 (12)
(12)
Компенсация влияния чистого запаздывания в замкнутых САУ
Для нейтрализации вредного влияния запаздывания используются регуляторы, которые компенсируют звено чистого запаздывания. Одним из таких способов компенсации является регулятор Смита. Структурная схема САУ с регулятором Смита представлена на рис.2.
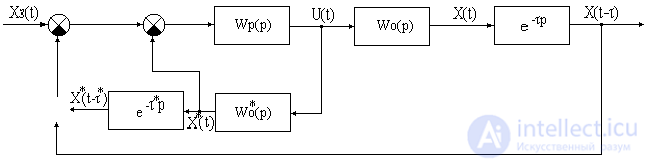
Рис.2.
Wp(p) - передаточная функция регулятора
Wo(p) - передаточная функция объекта
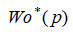 - передаточная функция модели объекта
- передаточная функция модели объекта
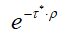 - передаточная функция модели запаздывания.
- передаточная функция модели запаздывания.
Применяя структурное преобразование схемы на рис.2, получим, что
передаточная функция замкнутой системы при
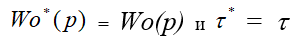
определяется следующим выражением:
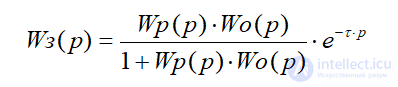 (13)
(13)
Из (13) видим, что, хотя запаздывание в системе сохраняется (физически это неизбежно), в характеристическом уравнении звено чистого запаздывания отсутствует. Следовательно, действие запаздывания на устойчивость и качество переходных процессов полностью скомпенсировано. Это является несомненным достоинством рассмотренного регулятора.
Недостатком регулятора является его чувствительность к изменениям параметров объекта, которое на практике всегда имеет место.
Телекоммуникации: при передаче данных по сетям задержки должны быть минимизированы, чтобы избежать потери качества связи.
Системы с запаздыванием тесно связаны с переходными процессами, так как наличие запаздывания существенно влияет на характер и динамику переходных процессов. Переходные процессы — это временные отклонения параметров системы от устойчивого состояния при воздействии на нее внешних факторов, таких как изменения входных сигналов или начальных условий. В системах с запаздыванием переходные процессы становятся более сложными и продолжительными, поскольку запаздывание создает дополнительную инерционность.
Увеличение времени переходного процесса: Запаздывание приводит к задержке в реакции системы на изменения внешних условий или сигналов, увеличивая время переходного процесса. Это замедляет достижение нового устойчивого состояния и делает систему более «инертной».
Колебательный характер переходного процесса: Запаздывания могут вызвать колебания в переходных процессах. Например, при больших задержках системы могут переходить в колебательный режим, даже если сами по себе они не являются осциллирующими. Это может привести к нестабильности, особенно если запаздывание переменное и случайное.
Устойчивость переходных процессов: В системах с запаздыванием устойчивость переходных процессов может значительно ухудшаться. Запаздывания добавляют «старые» значения в текущие расчеты, что может привести к накоплению ошибок и даже к расходимости, особенно если запаздывание существенно. Классические критерии устойчивости, такие как критерий Раута–Гурвица и критерий Найквиста, требуют корректировки при анализе систем с запаздыванием.
Эффект накопления ошибок: Из-за запаздывания отклонения от устойчивого состояния могут усиливаться по мере того, как система реагирует на «устаревшие» состояния. Этот эффект приводит к тому, что переходный процесс становится затяжным и сложным.
Для анализа переходных процессов в системах с запаздыванием используются специальные методы, учитывающие временные задержки:
Методы частотного анализа: Анализ систем с запаздыванием на частотной плоскости позволяет оценить влияние задержек на частотные характеристики системы и понять, как они влияют на устойчивость и колебания.
Численные методы: Для нелинейных систем или систем с переменным запаздыванием применяется численное моделирование, которое позволяет более точно описать переходный процесс с учетом всех параметров запаздывания.
Методы предсказания: В системах управления с запаздыванием используются алгоритмы предсказания, такие как предсказатель Смита. Этот метод компенсирует влияние запаздывания, прогнозируя поведение системы и позволяя осуществлять корректирующие воздействия с учетом будущих изменений.
Дифференциальные уравнения с запаздыванием (DDE): Уравнения с запаздыванием позволяют моделировать переходные процессы с учетом времени задержки. Эти уравнения учитывают зависимости текущего состояния от прошедших значений и более точно описывают переходный процесс.
Системы управления температурой: Переходный процесс нагрева объекта с запаздыванием отклика может длиться значительно дольше, чем без запаздывания. При этом запаздывание может вызвать перерегулирование температуры и нестабильные колебания.
Экономические модели: В экономике изменения, например, ставки налога, могут не сразу повлиять на состояние рынка. В таких случаях переходный процесс, связанный с адаптацией к новым условиям, может занять длительное время, вызывая осцилляции в рынке, которые усложняются запаздыванием.
Медицинские системы контроля: В системах мониторинга жизненных показателей организма запаздывание в реакции на корректирующие действия может привести к неустойчивым переходным процессам, если, например, система искусственной вентиляции легких реагирует на изменения дыхательных показателей с задержкой.
Теория систем с запаздыванием позволяет моделировать и анализировать широкий спектр реальных процессов, в которых отклик системы происходит не мгновенно. Она дает возможность разработчикам систем управления и ученым понять и компенсировать эффект запаздывания, повышая точность и стабильность таких систем. Запаздывание существенно влияет на переходные процессы, делая их более длительными, сложными и потенциально неустойчивыми. Теория систем с запаздыванием помогает анализировать и управлять такими переходными процессами, позволяя учитывать задержки для поддержания устойчивости и уменьшения колебаний.
Комментарии
Оставить комментарий
Моделирование и Моделирование систем
Термины: Моделирование и Моделирование систем