Примеры задач на графах кратко

Привет, сегодня поговорим про задачи на графах, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое задачи на графах , настоятельно рекомендую прочитать все из категории Алгоритмы и теория алгоритмов.

В данном разделе вы сможете ознакомится с прикладными задачами, которые решаются с помощью графов. Часть из задач имеет структуру, согласно которой достаточно просто правильно выбрать алгоритм и применить его для получения ответа. Другая часть требует некоторой модификации первоначального графа и комбинации нескольких алгоритмов для решения. В любом случае, все использованные алгоритмы описаны в теоретической части, что поможет Вам лучше понять методы решения задач.

Классические задачи на графах

Задача о кратчайшем пути (алгоритм Дейкстры, Беллмана, построение дерева путей). Задача на построение минимального остовного дерева (алгоритм Краскала). Задача о максимальном потоке в сети (алгоритм Форда-Фолкерсона). Задача о раскраске графа

Задачи

• Цепочка[поиск в глубину] алгоритм цепочка ,
• Путь [поиск в глубину] алгоритм поиска путей в графе ,
• Шестеренки [поиск в ширину] шестерёнки алгоритм графы ,
• Новогодняя вечеринка [максимальный поток] новогодняя вечеринка решение через графы ,
• Кубики [максимальный поток] кубики решение с использование графов ,
• Игра [максимальный поток] игра решение через графы ,
• Веревочный телеграф [минимальное остовое дерево (алгоритм Прима)] веревочный телеграф ,
• Secret Pipes [минимальное остовое дерево (алгоритм Крускаля)] secret pipes решение через графы ,
• Метро [минимальное остовое дерево (алгоритм Прима), поиск в глубину] метро решение через графы ,
• Network [минимальное остовое дерево (алгоритм Крускаля)] network решение через графы ,
• Олимпиада по алхимии [алгоритм Дейкстры] олимпиада по алхимии решение через графы ,
• Стены [алгоритм Флойда-Уоршелла] стены решение через графы ,
• Блокада [алгоритм Дейкстры] блокада решение через графы ,

Задача по теории графов с решением Характеристики графа

ЗАДАНИЕ.
Считая данный граф неориентированным, обозначить его вершины и ребра разными символами и определить.
3.1. Локальные степени и окружения каждой вершины в виде структуры смежности;
3.2. Об этом говорит сайт https://intellect.icu . Построить матрицы инцидентности и смежности;
3.3. Рассмотреть части графа. Привести примеры суграфа, накрывающего суграфа. Показать подграф, состоящий из трех вершин. Сколько таких подграфов можно найти в данном графе? Показать примеры пересечения и объединения частей графа;
3.4. Привести примеры циклического маршрута, цепи, простой цепи. Попытаться найти Эйлеров цикл;
3.5. Определить центр, диаметр и радиус графа. Считая граф ориентированным, определить
3.6. Степени вершин
3.7. Матрицы инцидентности и смежности.
3.8. Привести примеры пути, ориентированной цепи, простой цепи, контура, цикла и простого цикла.

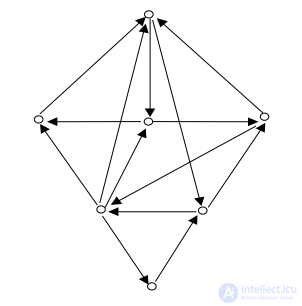
РЕШЕНИЕ.
Вводим обозначения:
=
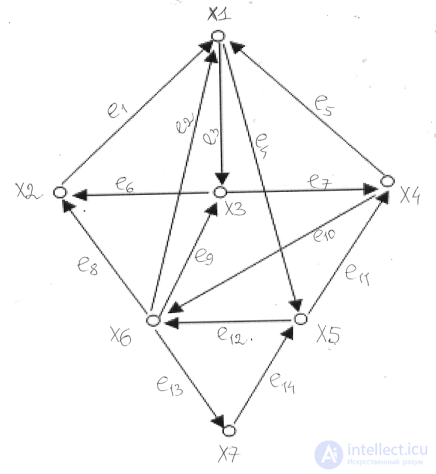Часть 1. Считаем граф неориентированным.
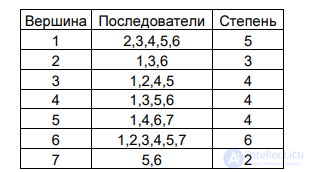
3.1. Найдем локальные степени и окружения каждой вершины в виде структуры смежности.

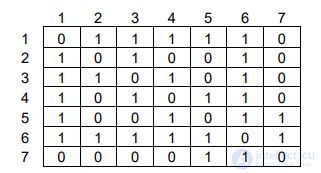
3.2. Построим матрицы инцидентности и смежности.

Строим матрицу инцидентности. Элемент матрицы b_ij = 1, если вершина xi инцидентна ребру ej , в противном случае равен 0. Получаем:

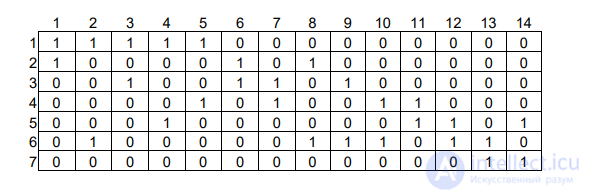
Строим матрицу смежности для этого графа. Элемент матрицы ij a равен 1, если вершиныx i и x j смежны, в противном случае равен 0. Получаем:

3.3. Рассмотрим части графа.
Суграф (граф с таким же множеством вершин):

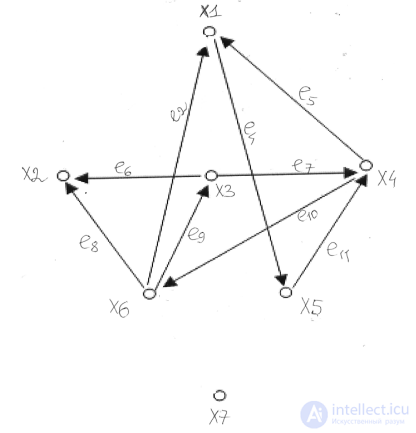
Накрывающий суграф (без изолированных вершин):

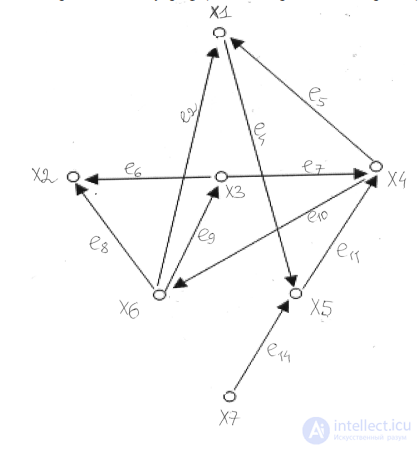
Подграф, состоящий из трех вершин.

Подграфов из трех вершин в графе, состоящем из 7 вершин, будет 3

подграфов.
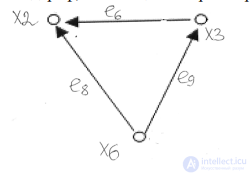
Покажем примеры пересечения и объединения частей графа.
Пусть даны две части графа:

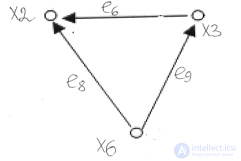
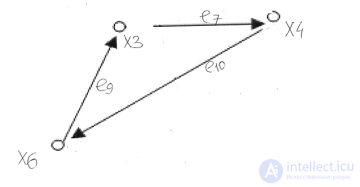
Тогда их объединение:

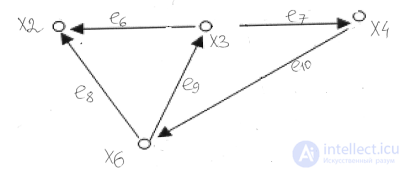
Их пересечение:

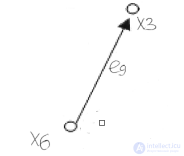
3.4. Приведем примеры

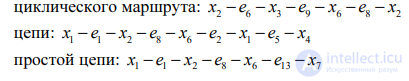
Найдем Эйлеров цикл (содержащий все ребра графа по одному разу). Известно, что граф является эйлеровым тогда и только тогда, когда степень каждой из его вершин – четное число. Степени вершин были найдены выше, они не все четные, поэтому эйлеров цикл не существует.

3.5. Определим центр, диаметр и радиус графа.
Построим матрицу расстояний для графа.



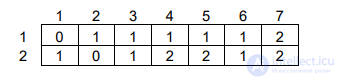
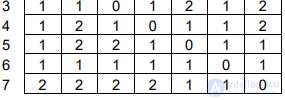
Построим вектор удаленностей (эксцентриситетов вершин) (максимальное число в каждой
строке) d = (2, 2, 2, 2, 2, 1, 2).
Диаметр графа равен 2.
Радиус графа равен 1.
Центральная вершина
x6 образует центр графа. Остальные вершины периферийные.

Часть 2. Считаем граф ориентированным.

3.6. Найдем степени вершин, результаты занесем в таблицу:

3.7. Построим матрицы инцидентности и смежности.
Строим матрицу инцидентности. Элемент матрицы b _ij =1 , если из вершиныx i исходит дуга ej , b ij = −1 , если в вершину x i входит дуга ej , в противном случае равен 0.

Получаем:


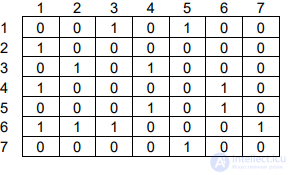
Строим матрицу смежности для этого графа. Элемент матрицы ij a равен 1, если из
вершины i
x в вершину j
x ведет дуга, в противном случае равен 0. Получаем:

3.8. Приведем примеры

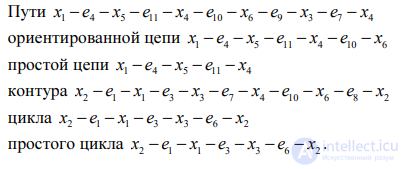
На этом все! Теперь вы знаете все про задачи на графах, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое задачи на графах и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Алгоритмы и теория алгоритмов