Игра (решение через графы)

Привет, сегодня поговорим про игра решение через графы , обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое игра решение через графы , настоятельно рекомендую прочитать все из категории Алгоритмы и теория алгоритмов.

Белорусская олимпиада по информатике, 2001

Задание

Известная на весь Могилев компания выпустила игру, для которой необходима конструкция, состоящая из маленьких платформ и труб. Платформы разделяются на стартовые (их N1 штук), финишные (N3 штук) и промежуточные (N2 штук). Все стартовые платформы находятся на одинаковой высоте. Финишные платформы также находятся на одинаковой высоте. Все высоты промежуточных платформ различны. Они меньше высоты стартовых, но больше высоты финишных.

Каждой платформе соответствует уникальный номер от 1 до Nl+N2+N3. Нумерация следующая: сначала перечислены все стартовые платформы, затем промежуточные и, наконец, финишные. Все промежуточные платформы пронумерованы по убыванию высоты. То есть если высота промежуточной платформы А больше высоты платформы В, то номер А меньше номера В.

На каждой из стартовых платформ находится шарик. Шарик может скатиться с платформы А на платформу В, если они соединены трубой и высота А больше высоты В. На каждой из финишных платформ может оказаться не более одного шарика. Если шарик находится на некоторой платформе, то игрок может выбрать направление дальнейшего пути шарика, то есть выбрать платформу, на которую шарик скатится. Также для каждой промежуточной платформы задано число С, равное максимальному количеству шариков, которые могут прокатиться по ней за время игры. Цель игры заключается в том, чтобы на финишных платформах оказалось как можно больше шариков.

Нужно узнать, какое максимальное количество шариков может оказаться на финишных платформах в результате игры.

Ввод

Во входном файле Game.in находится информация о конструкции в следующей форме:

N1 N2 N3 
CN1+1 
..
CNl+N2 
K1 A[1.1] : A[1.K1] 
K2 A[2.1] : A[2.K2] 
..
KNl+N2A[Nl+N2.1] : A[Nl+N2.KNl+N2] 

где числа N1, N2, N3 — соответственно количество стартовых, промежуточных и финишных платформ. Об этом говорит сайт https://intellect.icu . Cj — максимальное количество шариков, которые могут прокатиться по промежуточной платформе с номером j (N1+1 <= j <= N1 + N2) за все время игры. Ki — количество труб, выходящих из платформы с номером i (1 <= i <= N1 + N2).

Элементы массива A, перечисленные в строке, являются номерами платформ, на которые может скатиться шарик с соответствующей платформы.

Ограничения: 
Все числа на вводе целые.

0 < N1. N2. N3 < 51 
1 < Nl+N2+N3 < 201 
0 J Cj J 50 

Не существует труб между стартовыми платформами. Не существует труб между финишными платформами.

Вывод

В первой строке должно находиться единственное число, равное максимальному количеству шариков, которые могут оказаться на финишных платформах в результате игры.

Пример ввода          Пример вывода 
3 4 3                 2 
3 
2 
1 
2 
1 4 
1 4 
1 4 
2 5 6 
1 7 
1 7 
3 8 9 10 

Решение     [вверх]

Стартовые, промежуточные и финишные платформы естественно представлять вершинами графа, а трубы между ними — дугами. Однако данная задача слегка отличается по постановке от классической, поскольку здесь задан вес вершины:«...для каждой промежуточной платформы задано число С, равное максимально- му количеству шариков, которые могут прокатиться по ней за время игры». Для перехода к классической постановке достаточно заменить такие вершины на дуги. При этом введенным дугам присваивается вес замененных вершин. Понятно, что должны появиться дополнительные вершины.

 
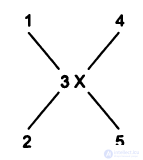
Например, пусть в вершину 3 с весом X входит две дуги (1 -> 3 и 2 -> 3) и выходит две дуги (3 -> 4 и 3 -> 5), как показано на рисунке. Мы добавляем вершину 6 и дугу 3 -> 6 с весом X.

Поскольку промежуточные платформы превращаются в дуги, то всего вершин становится на N2 больше, где N2 — количество промежуточных платформ.

Добавляем исток и связываем его с вершинами, соответствующими стартовым платформам. Пропускная способность дуг равна 1, поскольку по условию задачи на каждой из стартовых платформ находится шарик.

Для каждой промежуточной платформы с номером /добавляем две вершины с но- мерами N1 + i и all + i (где all = N1 + N2 + N3) соответственно. Добавляем также дугу между этим вершинами с пропускной способностью вершины.

Все входящие дуги от стартовых платформ будем строить в вершины M+i. По условиям задачи их пропускная способность не ограничена. Все дуги от промежуточных платформ будем строить от вершин all + i — их пропускная способность также не ограничена.

Добавляем вершину-сток с дугами к ней от всех финишных платформ. Веса этих дуг равны 1, поскольку на каждой из финишных платформ может оказаться не более одного шарика.

Для вывода ответа на поставленный в задаче вопрос «Какое максимальное коли- чество шариков может оказаться на финишных платформах в результате игры?» после построения максимального потока пометоду Форда-Фалкерсона достаточно просуммировать количество шариков, выкатившихся из истока на стартовые платформы.

 
Начальный граф для задачи из примера .

  Граф задачи после преобразования (над ребрами указана их пропускная способность)

Формальное описание     

Game()
1. Считать входные данные задачи из файла.
2. Создать граф, в котором вершины - платформы. Связать вершины, которые
   соединены трубами.
3. Создать для каждой промежуточной платформы создать вершину и связать ее
   с вершинами, с которыми была связана текущая вершина.
4. Связать текущую промежуточную вершину с созданной. Пропускную 
   способность задать равной ограничению для текущей вершины.
2. Создать вершину-исток и соединить ее с вершинами графа, которые
   отвечают стартовым платформам. Пропускная способность для этих ребер
   равна единице.
3. Создать вершину-сток и соединить ее с финишными платформами. 
   Пропускная способность ребер равна 1.
4. Найти максимальный поток по алгоритму Форда-Фалкерсона 
   между истоком и стоком.
5. Подсчитать поток между истоком и стартовыми платформами и вывести его. 

 

На этом все! Теперь вы знаете все про игра решение через графы , Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое игра решение через графы и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Алгоритмы и теория алгоритмов

Из статьи мы узнали кратко, но содержательно про игра решение через графы