2.2. Теорема деления по Вейерштрассу- как фундаментальный результат теории особенностей, сущность и назначение

Приведем один фундаментальный результат теории особенностей, использующий понятие кратности функции по одной переменной.

ТЕОРЕМА 2.1 (деления). Пусть F(x; y) : гладкая функция от m+ 1 переменных.

Если 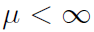кратность функции F по х в точке 0, то в окрестности 0 функция F(x; y) представима в виде

, (2.3)

где ai(y) и φ(x; y) - гладкие функции, ai(0)=0 и φ(x; y) 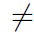0

ЗАМЕЧАНИЕ 2.2. Теорема 2.1 имеет локальный характер.

Разумеется, она справедлива не только для начала координат, но и для произвольной точки (общий случай получается с помощью сдвига начала, координат).

Эта теорема справедлива и для аналитических функций:

в ее формулировке нужно везде заменить слово «гладкий» словом «аналитический».

Впервые она была доказана Вейерштрассом для аналитических функций комплексных переменных ( голоморфных функций комплексных переменных). Голоморфная функция или однозначная комплексная аналитическая функция (от греч. ὅλος — «весь, целый» и μορφή — «форма»), иногда называемая регулярной функцией — функция комплексного переменного, определенная на открытом подмножестве комплексной плоскости и комплексно дифференцируемая в каждой точке.

В отличие от вещественного случая, это условие означает, что функция бесконечно дифференцируема и может быть представлена сходящимся к ней рядом Тейлора.

Голоморфные функции также называют иногда аналитическими, хотя второе понятие гораздо более широкое, так как аналитическая функция может быть многозначной, а также может рассматриваться и для вещественных чисел.

Аналитический ее вариант часто называется «подготовительной теоремой Вейерштрасса».
Гладкий вариант (приведенный выше) иногда называют «теоремой деления Мальгранжа» или «теоремой деления Мазера».
Мы приведем доказательство теоремы 2.1 для аналитических функций (см. раздел 12).

Доказательство в гладком случае получается из аналитического при помощи техники, подобной леммам из раздела 5.3. Его можно найти, например, в книгах |9, 15].

Суть теоремы деления

Суть теоремы деления (Weierstrass division theorem, Malgrange–Mather division theorem) в том, что она описывает, как устроена гладкая функция около особой критической точки конечной кратности по одной переменной.

Если сказать простыми словами:

• У нас есть функция f(x,y1,…,yn), зависящая от одной «особенной» переменной x и еще nnn параметров y.

• В точке 0 она имеет критическую точку по xxx, причем производные по x до порядка μ\muμ включительно обнуляются, а производная порядка μ+1 не равна нулю.
  То есть x=0 — это корень кратности μ+1 (по переменной x) для функции при фиксированных y=0.

Тогда теорема утверждает:
вблизи нуля f можно представить как произведение невырожденного множителя φ(x,y) (который не обнуляется) и многочлена по x степени μ+1, коэффициенты которого ai(y) зависят от параметров y и обращаются в ноль при y=0.

Формально:

Интуиция:

• Это аналог теоремы Вейерштрасса для многочленов: если многочлен имеет корень кратности μ+1, то его можно разложить в вид «невырожденная часть × (многочлен с данным корнем)».

• В случае гладких (или голоморфных) функций теорема говорит, что локально вокруг особой точки все сводится к такой «многочленной форме» по выделенной переменной.

Зачем нужно:

• Теорема деления — фундамент в сингулярностях функций (Тома, Мальгранжа, Мазера).

• Она позволяет свести анализ поведения функции около особой точки к анализу многочлена, что сильно упрощает классификацию критических точек и их инвариантов.