Лекция
Привет, Вы узнаете о том , что такое силлогизм, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое силлогизм, простой категорический силлогизм, категорический силлогизм, теория силлогизмов аристотеля, модусы силлогизма, фигуры силлогизма , настоятельно рекомендую прочитать все из категории Логика.
Силлогизм категорический – дедуктивное умозаключение, в котором
из двух суждений, имеющих субъектно-предикатную форму следует новое суждение (заключение), имеющее также субъектно-предикатную форму. Аристотель первый осознал формальную сторону силлогизмов, т.е. их независимость от конкретного содержания, а введя буквенные cимволы для обозначения переменных, Аристотель заложил основы формального построения логики.
Силлогизмы Аристотеля состоят из двух суждений, связанных общим средним термином, из которых следует третье суждение, также имеющее субъектно-предикативную форму. При этом средний термин в заключение не входит. Аристотель рассматривал четыре типа суждений:
A (S,P) – общеутвердительное: “все S суть P”;
E (S,P) - общеотрицательное: “ни одно S не есть P” ;
I (S,P) - частноутвердительное: “некоторые S суть P”;
O (S,P) – частноотрицательное: “некоторые S не суть P”.
Здесь S – класс предметов, а P - свойство.
Суждение, в котором содержится общее свойство, называется большой посылкой; суждение, содержащее частный случай, - малой посылкой; а третье суждение – заключение силлогизма. В зависимости от положения малой посылки различаются четыре фигуры силлогизма (где X прини мает значения A, E, I, O) :

Одной фигуре соответствует 64 модуса, а всего для четырех фигур имеется 256 модусов. Из всех модусов верны только 19 (отмеченные * верны для непустых множеств), имеющие следующие названия:

Гласные буквы в названиях силлогизмов есть значения X. Так что
модусы 1-й фигуры: AAA, EAE, AII, EIO; модусы 2-й фигуры: EAE, AEE, EIO, AOO; модусы 3-й фигуры: AAI, IAI, AII, EAO, OAO, EIO; модусы 4-й
фигуры: AAI, AEE, IAI, EAO, EIO.
Можно доказать истинность силлогизмов, используя теоретико-множественную интерпретацию, где P означает область истинности предиката Р(x); тогда суждения A, E, I, получают следующую интерпретацию:
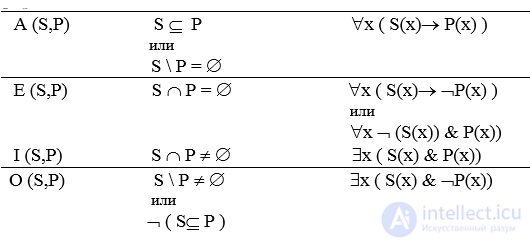
Каждое силлогическое умозаключение можно изобразить с помощью трех кругов (S,P и M) Эйлера, причем из взаимного положения кругов S и P к M можно наглядно заключить об отношении S к P.
Так силлогизм:
Все люди могут ошибаться (MAP);
Все ученые – люди (SAM);
Все ученые могут ошибаться (SAP);
может быть наглядно изображен следующим образом:

Другой пример:
Люди не могут изменить объективные законы природы (MEP);
Ученые – люди (SAM);
Ученые не могут отменить объективные законы природы (SEP);
имеет теоретико-множественное представление:
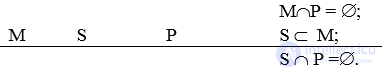
Пример доказательства модуса BARBARA:
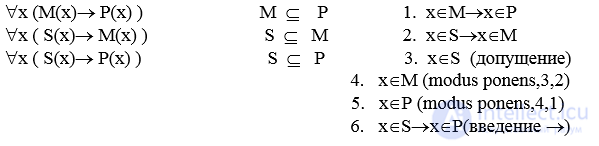
Аристотель разработал правила сведения одних силлогизмов к другим (перестановки посылок, приведение к невозможному, выделение части одного из терминов), что являлось предпосылкой к аксиоматичес кому построению силлогистики.
Пример сведения силлогизма AAI :
Все звезды светят собственным светом;
Все звезды – небесные тела;
Некоторые небесные тела светят собственным светом;
к силлогизму AII:
Все звезды светят собственным светом;
Некоторые небесные тела – звезды;
Некоторые небесные тела светят собственным светом.
Упражнение
1. Изобразить модусы с помощью кругов Эйлера и доказать теоретико–множественными средствами.
2. Доказать силлогизмы Аристотеля, используя правила вывода исчисления высказываний.
4. Сделайте выводы с помощью правил силлогизма:
4.1 Все врачи имеют общее образование. Некоторые врачи – терапевты.
4.2 Все сочинения А.П.Чехова нельзя прочитать за один день. Рассказ “Попрыгунья” - сочинение А.П.Чехова.
4.3. “Петр 1 … разорвал покров таинственности, окутывающий царскую особу, и с отвращением отбросил от себя византийские обноски, в которые рядились его предшественники. Петр 1 не мог удовольство ваться жалкой ролью христианского далай-ламы, разукрашенного парчей и драгоценными камнями, которого издали показывали народу, когда он торжественно следовал из своего дворца в Успенский собор и из Успенского собора во дворец. Петр 1 предстает перед своим народом, словно простой смертный. Все видят, как этот неутомимый труженик, одетый в скромный сюртук военного покроя, с утра до вечера дает приказания и учит, как надо их выполнять: он кузнец, столяр, инженер, архитектор и штурман. Его видят везде, без свиты, - разьве только с одним адъютантом, - возвышающегося над толпой благодаря своему росту… Петр Великий был первой свободной лично стью в России и, уже по одному этому, коронованным революционером” (Герцен А.И. О развитии революционных идей в России//Собр.соч.Т.3.С.388).
4.4. На вопрос доктора Уотсона, каким образом Холмс узнал, что он утром был на почте и отправил телеграмму, последний сказал следующее: “…мне известно, что утром вы не писали никаких писем, ведь я все утро сидел напротив вас. А в открытом ящике вашего бюро я заметил толстую пачку почтовых открыток и целый лист марок. Для чего же тогда идти на почту, как не за тем, чтобы послать телеграмму? Отбросьте все, что не могло иметь места, и останется один-единственный факт, который и есть истина”(Конан-Дойль А. Собр.соч.)
4.5. Внимательно осмотрев комнату, в которой совершено преступление, Шерлок Холмс сказал доктору Уотсону следующее:
«Мало иметь хороший ум, главное - хорошо его применять» Р. Декарт
Все люди от природы стремятся к знанию
Силлогизм (от. греч. sillogismos - со- считывание) - классическая тема логики. Учение о силлогизме было изложено Аристотелем (384 - 322 до н.э.) в «Аналитике». В своих исследованиях он опирался на Демокрита и Платона. Согласно Аристотелю, силлогизм есть демонстративное умозаключение, в котором вывод по законам логики следует с необходимостью. В нефилософской литературе термином «силлогизм» иногда обозначают любое демонстративное умозаключение.
Аристотель разделяет умозаключения на виды по способу и характеру получения логического вывода: «Умозаключение есть речь, в которой если нечто предположено, но через положенное из него с необходимостью вытекает нечто отличное от положенного. Доказательство имеется тогда, когда умозаключение строится из истинных и первых [положений] или из таких, знание о которых берет свое начало от тех или иных первых и истинных [положений]. Диалектическое же умозаключение - это то, которое строится из правдоподобных [положений]. Истинные и первые [положения] - те, которые достоверны не через другие [положения], а через самих себя... . Правдоподобно то, что кажется правильным всем или большинству... . Эристическое же умозаключение исходит из [положений], которые кажутся правдоподобными, но на деле не таковы... .
Кроме всех указанных видов умозаключений имеются и паралогизмы, которые строятся на основании того, что свойственно той или иной науке...: здесь не принимают того, что кажется правильным всем» .
Аристотель изобретает силлогизм как практическое орудие, или «органон», для приведения в связь друг с другом демонстративных умозаключений. Состоит аристотелевский силлогизм из 3 суждений, два из них посылки, а третье - заключение.
Силлогизм - дедуктивное умозаключение, в котором из двух суждений, имеющих субъектно-предикатную форму (S - Р), следует новое суждение (заключение), имеющее также субъектно-предикатную форму (S - Р). Следует добавить, что посылки должны быть распределены, во-первых, по логическому квадрату (А, Е, I, О), во-вторых, иметь средний термин (М).
В.А. Светлов в «Практической логике» добавляет к характеристике силлогизма следующее. Все шесть терминов должны входить в состав одного умозаключения. Одна из посылок содержит субъект (S) заключения и исключающий термин (М), другая - предикат (Р) заключения и исключающий термин (М). Средний термин (М) и есть тот самый исключающий термин - в посылках он есть, а в заключении отсутствует. Суждения в силлогизме связаны друг с другом логическим следованием и средним термином . Правда, у В.А. Светлова термины силлогизма, как и Я. Лукасе- вича, обозначаются буквами А, В, С, где В - средний термин. Нам ближе общепринятая классификация терминов силлогизма.
Наконец, силлогизм есть умозаключение, в силу которого, признав истинность посылок, нельзя не согласиться с истинностью заключения при условии соблюдения соответствующих правил логического следования. Об этом говорит сайт https://intellect.icu . Обратимся к самой простой характеристике силлогизма.
Вернемся к нашему примеру.

Посылки стоят над чертой, а заключение - под чертой. Три понятия (класса), о которых идет речь, именуются терминами силлогизма, при этом субъект заключения (в нашем примере - понятие «Сократ») называется меньшим термином, а предикат («смертен») - большим термином. Меньший и больший термины называются крайними и обозначаются соответствующими символами S и Р. Термин, входящий в посылки, но отсутствующий в заключении («человек») именуется средним термином и обозначается символом М.
Посылкам силлогизма также присваиваются специальные названия. Та из них, в состав которой входит больший термин (Р), называется большей посылкой; та, которая содержит меньший термин (S), называется меньшей посылкой. Большая посылка всегда содержит термины Р и М, меньшая - термины S и М, заключение - термины S и Р. В силлогизме названные элементы структуры умозаключения располагаются в следующем порядке: большая посылка, меньшая посылка, заключение. Конъюнкцию посылок можно рассматривать как логическое основание, а заключение - как логическое следствие: А л А —> А (см. логический квадрат). В силлогизме, т.е. в данном умозаключении, как и во всяком логическом выводе, есть свои правила. Их можно проиллюстрировать с помощью круговых схем Эйлера.

Рис. 1.1. Демонстративный силлогизм по модусу Barbara (AAA) Иными словами, если всякий человек смертен, а Сократ - человек, то и он тоже смертен. Но не наоборот: не всякий смертный - человек. Данное умозаключение (логический вывод) построено по первой фигуре. Именно такое расположение терминов есть в первой фигуре.
Однако совсем не обязательно такое расположение терминов и модусов можно встретить во всяком силлогизме (об этом в другом параграфе). Такие силлогизмы Аристотель называл диалектическими, где вывод правдоподобен, а недостоверен.

Рис. 1.2. Соотношение терминов в недемонстративном умозаключении
Данный логический вывод является правдоподобным, ибо в нем возможны ответы: либо Петров входит в класс «философов-шахматистов», либо в класс «философов - нешахматистов»1. Иными словами, логический вывод о том, что Петров является «хорошим шахматистом» с необходимостью не следует.
Аристотель в «Аналитике» описывает строение силлогизма: «Посылка есть речь, утверждающая или отрицающая что-то относительно чего-то. Она бывает или общей, или частной, или неопределенной. Общей я называю [посылку] о присущем всем или не присущем ни одному, частной - о присущем не всем, неопределенной - о присущем или неприсущем без указания того, общая ли она или частная...
Термином я называю то, на что распадается посылка, т.е. то, что сказывается, и то, о чем оно сказывается, с присоединением [глагола] «быть» или «не быть»; силлогизм же есть речь, в которой, если нечто предполо-
Круговые схемы Эйлера - самый простейший способ проверки истинности вывода в силлогизме.
жено, то с необходимостью вытекает нечто отличное от положенного в силу того, что положенное есть. Совершенным я называю силлогизм, который для выявления необходимости не нуждается ни в чем другом, кроме того, что принято; несовершенным же - силлогизм, который нуждается [для этого] в чем-то одном или многом, что хотя и необходимо через данные термины, но через [данные] посылки не получено» .
По Аристотелю, силлогизм представлен в иной форме, незнакомой современному читателю. Во-первых, Аристотель не пользовался практически примерами; вместо терминов-слов у него буквенные символы. Во-вторых, аристотелевский силлогизм записывается в форме условнокатегорического умозаключения. В-третьих, ни один силлогизм Аристотелем не формируется как вывод со словом «следовательно». В- четвертых, четвертая фигура Аристотелем не используется. Иногда Аристотель использует примеры (живое существо - человек - лошадь) для наглядности, но крайне редко. Умозаключения в «Аналитике» описываются чаще всего с помощью символов. В-пятых, совершенный силлогизм построен по первой фигуре (см. пример 13.1.1). Это умозаключение Аристотель описывает так: «Если три термина так относятся между собой, что последний термин целиком содержится в среднем, а средний целиком содержится в первом или вовсе не содержится в нем, то для этих крайних терминов необходимо имеется совершенны силлогизм» .
Силлогизм 13.1.1 практически во всех учебниках по логике рассматривается как пример аристотелевского совершенного силлогизма. Но Аристотель не вводил в «Аналитику» единичные термины («Сократ - человек»). По Аристотелю, он выглядел бы иначе:

Именно в импликации записывается аристотелевский силлогизм. Аристотель редко использует термины-слова, в «Аналитике» он чаще включает символы в силлогизм:

Наконец, Аристотель в первой посылке предикат ставит на место среднего, а во второй субъект на место среднего:

В такой форме представляет аристотелевский силлогизм польский логик Я. Лукасевич .
простой категорический силлогизм - дедуктивное демонстративное умозаключение, в котором из двух суждений, имеющих субъектнопредикатную форму, следует новое суждение (заключение), имеющее также субъектно-предикатную форму. В простом категорическом силлогизме различают: 1) посылки, 2) термины, 3) заключение.
Термины S - М - Р, где S (субъект) - меньший термин (понятие, находящееся во второй посылке), М - средний термин (понятие, встречающееся в обеих посылках), Р (предикат) - больший термин (понятие, находящееся в первой посылке). В любом силлогизме можно встретить субъект, предикат, средний термин.
Посылки - это суждения, выраженные в форме предложений. Одна из них выражает отношение меньшего термина (S) к среднему (М). Она называется «меньшей посылкой» и находится всегда на втором месте. Другая выражает отношение большего термина (Р) к среднему (М). Она называется «большей посылкой» и всегда находится на первом месте. Заключение в силлогизме всегда имеет логическую форму S - Р.

Хариты. Ill в. до н.э.
Материю видит перед собою всякий; содержание находит лишь тот, кто имеет с ним дело; форма же остается тайной для большинства» (И. Гете).
Форма - это общее и наиболее существенное, что есть во всякой реальности (природе, обществе, мышлении). В сфере мышления форма олицетворяет собой наиболее общие правила построения мыслей - дедуктивных и индуктивных. Форма мышления - есть и языковое строение мышления («понятие - имя», «суждение - высказывание», «умозаключение - логический вывод»).
Для правильного понимания смысла понятия «форма» приведем пример из теории государства и права. Всякий цивилист хорошо знает, что государства различаются по национальным, территориальным и иным признакам (организацией политической власти, государственным устройством, социальным управлением делами общества, правовым статусом, типами политического режима, наличием в государстве конституционных прав и свобод человека и гражданина и др.). Иными словами, нет и не может быть двух одинаковых государств.
Тем не менее чисто теоретически во всем многообразии национальных и территориальных государственных устройств можно выделить только две формы правления - монархию и республику. Монархия и республика - формы государственного правления. В свою очередь монархия может быть двух видов - абсолютная и парламентарная; республика - президентская, парламентарная, смешанная. К логической характеристике государства добавим определение формы государства - это есть организация политической власти, включающая в себя форму правления, форму государственного устройства и форму политического режима.
Итак, форма - это внутреннее устройство всякой реальности (в том числе - правовой), а в теоретическом плане - это еще и абстрактно-логическая модель реальности.
Скульптурная модель древних Харит олицетворяет собой античное понимание внутренней идеи красоты женского тела - сияющей, благомыслящей, цветущей доброты вечно юной женской природы.
Здесь же представлена идея единой формы красоты женского тела. В скульптурной композиции - 3 фигуры. Согласно древней легенде, Харит (дочерей великого Зевса) звали: Аглая («сияющая»), Евфросина («благомыслящая»), Талия («цветущая»). Они не случайно представлены античным скульптором обнаженными. Древний Мастер хотел тем самым подчеркнуть, что форма - это не внешнее одеяние.
Несмотря на то, что в композиции - три фигуры, на самом деле, если внимательно присмотреться, мы обнаружим одну фигуру - «фигуру - форму - идею» женской красоты. Согласно более древней легенде, Гомеру была известна только одна дочь Зевса - Харита. X а р и т а - есть идея о вечной (универсальной) юности и красоте. Она может иметь бесконечное множество обличий, но как формальная идея вечной юности и красоты - она одна, представленная неизвестным скульптором в обнаженном виде. Еще раз напомним слова великого И. Гете: «Материю видит перед собою всякий...; форма же остается тайной для большинства».
Как это не парадоксально звучит, но фигуры и модусы силлогизма - универсальные и общие формальные структуры дедуктивных умозаключений, состоящих из двух суждений, имеющих субъективно-предикатную форму, логический вывод которых основан на отношении двух крайних терминов (S и Р) к среднему (М): S - М - Р.
Фигуры силлогизма - своеобразная форма духа и сущности простого категорического силлогизма. Фигуры и модусы силлогизма - «обнаженная» форма дедуктивных демонстративных умозаключений:
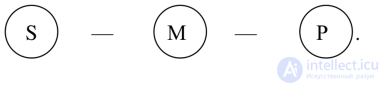
В зависимости от положения в посылках среднего термина (М) различают четыре фигуры силлогизма (3 - аристотелевские, 1 - галеновская). Вместе они представляют один тип демонстративных умозаключений - простой категорический силлогизм. Предикат находится в большей посылке, субъект - в меньшей посылке. Средний термин (М) - обеих посылках. Схемы показывают расположение субъекта, предиката, среднего термины в силлогистических выводах:
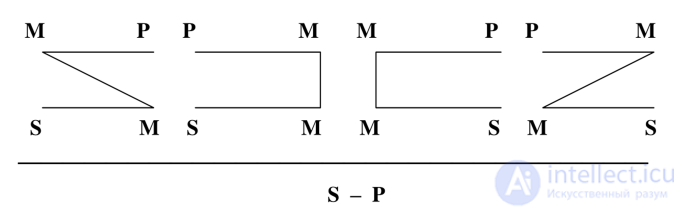
Рис. 2.1. Фигуры и термины силлогизма
Под чертой находится заключение (S - Р). Заключение в силлогизме всегда имеет форму S - Р .
Пример 1-й фигуры
Пример 2-й фигуры
Пример 3-й фигуры
Пример 4-й фигуры
ния или S относительно М, а М относительно Р, или М относительно их обоих, или же их обоих относительно М. Это и есть способ построения фигур силлогизма.
Первую фигуру Аристотель называет классической и часто сводит умозаключения по остальным двум к первой. Аристотель считает, что только по первой фигуре вывод следует с необходимостью: «Если А сказывается обо всех Б, а Б - обо всех В, то А необходимо сказывается обо всех В» . Силлогизмы второй и третьей фигур несовершенны, так как необходимы дополнительные операции сведения их к первой, чтобы достичь логической необходимости следования.
В первой фигуре (при утвердительных посылках) средний термин выражает причину. В других фигурах силлогизма такой ясности нет. Очень редко встречаются логические выводы по четвертой фигуре. По крайней мере, подобрать примеры очень трудно. В учебных пособиях она, как правило, не упоминается. Видимо еще потому, что процедура логического вывода четвертой фигуры сводится обычно к первой.
Умение различать фигуры силлогизма имеет чисто практическое значение. Дело в том, что каждая фигура отображает различные приемы оперирования посылками. Так, если требуется доказать истинность единичного и частного суждения, используется первая фигура, когда единичный или частный случай подводится под общее правило. Если требуется опровергнуть единичное утвердительное суждение, можно использовать вторую фигуру силлогизма. Для опровержения общих суждений используется третья фигура (Н.И. Кондаков).
В связи с тем, что все умозаключения по фигурам силлогизма можно свести к первой, рассмотрим в полном объеме действие первой фигуры в мышлении. В 1-й фигуре два крайних термина (S и Р) могут взаимно включать или исключать друг друга через посредство третьего. Заключение принимает все возможные (четыре) высказывания по логическому квадрату: А, Е, I. О. Эти операции проходят следующим образом. Далее будут показаны в круговых схемах расположение терминов и посылок в первой фигуре.
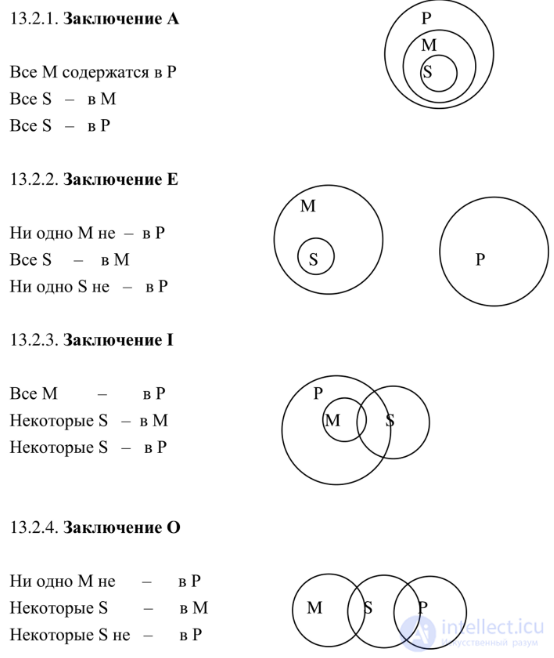
Эти четыре формы составляют модусы первой фигуры. Если какое-либо доказательство можно привести к этим формам и если вы принимаете его посылки, то вы должны, раз вы хотите быть последовательны, допустить и заключение. В противном случае вам придется отрицать очевидное и достоверное[10]. Мы видим, что если М всецело лежит в Р или вне Р, a S всецело или отчасти в М, то S всецело или отчасти лежит в Р или вне его.
Но если мы попробуем поставить термины посылок первой фигуры в какие-нибудь другие взаимные отношения, то найдем, что тут уже ничего нельзя сказать о положении S относительно Р. Если большая посылка не общая, т.е. если М не лежит всецело в Р или вне его, то никакого заключения вывести нельзя, какова бы ни была меньшая посылка. Предположим при этом, что в меньшей посылке дано: «Все S содержатся в М»; очевидно, что в этом случае может быть истинным как «Все S содержатся в Р» (А), так и «Ни одно S не содержится в Р» (Е), и «Некоторые S содержатся в Р» (I), и «Некоторые S не содержатся в Р» (О)[11]:

Иными словами, положение S неопределенно. В результате логический вывод с необходимостью не следует. И наконец, если меньшая посылка в первой фигуре не утвердительная, то вероятность заключения увеличивается в несколько раз.
Модусы простого категорического силлогизма - это разновидности силлогизма, отличающиеся друг от друга качественной и количественной характеристикой входящих в них посылок и заключения.
Каждая фигура имеет свои модусы (или формы), применение которых дает истинное заключение[12].
Общее количество сочетаний суждений, различаемых по количеству и качеству (А - Е - I - О), в посылках и заключении силлогизма для каждой фигуры равно 64. Если же принять во внимание особенности расположения терминов в фигурах, то теоретически можно говорить о 256 модусах силлогизма. Однако лишь незначительная их часть является основой правильных демонстративных умозаключений. Некоторые сочетания вообще не имеют места (например, две отрицательные посылки, когда вывод в принципе невозможен). Другие же сочетания невозможны из-за особых правил фигур и т.д. В результате остается 19 модусов, которые принято называть правильными. Остальные модусы - неправильные (они не могут быть основой демонстративных выводов). Но в «Словаре по логике» все- таки приводится другая цифра - 24[13]. Разница в так называемых «ослабленных» модусах, в которых мы получаем заключение типа I и О, хотя можем получить соответственно суждения А и Е. Итак, правильных модусов в силлогизме 19:
модусы 1-й фигуры: AAA, ЕАЕ, АП, ЕЮ;
модусы 2-й фигуры: ЕАЕ, АЕЕ, ЕЮ, АОО;
модусы 3-й фигуры: AAI, IAI, All, ЕАО, ОАО, ЕЮ;
модусы 4-й фигуры: AAI, АЕЕ, IAI, ЕАО, ЕЮ.
В средневековых университетах были составлены графические схемы модусов силлогизма. Иногда, для лучшего запоминания форм силлогизма, сочинялись поэмы (логические высказывания в стихах легче запоминались). В XIII в. в университетах был распространен «логический квадрат Боэция» специально для запоминания модусов силлогизма. Один из вариантов записей модусов представлял собой следующую форму:
Barbara, Celarent, Darii, Ferio;
Cesare, Camestres, Festino, Baroco;
Darapti, Disamis, Datisi, Felapton, Bocardo, Ferison;
Bramantip, Camenes, Dimaris, Fesapo, Fresison.
Первая гласная указывает на количество и качество большей посылки. Вторая - на количество и качество меньшей посылки. Третья - количество и качество заключения.
Начальные согласные В, С, D, F указывают на тот модус первой фигуры, к которому его можно редуцировать. Так силлогизм «Вагосо» второй фигуры можно привести к силлогизму «Barbara», «Disamis» третьей фигуры - «Darii» первой и т.д.
Согласные буквы S, Р, М, С указывают на возможность логических операций: a) S означает, что предложение, обозначаемое той гласной, после которой оно стоит, подлежит простому обращению («conversio simplex»).
2
Так, «Festino» конверсирует, т.е. субъект заменяет предикат без изменения количества, в модус «Ferio» первой фигуры; б) Р означает, что предложение, обозначаемое гласной, после которой эта буква стоит, должно быть обращено через ограничение («per т accidens»); в) М означает, что посылки взаимно обратимы, большая становится меньшей и наоборот; г) С означает редукцию к невозможному, демонстрируя, что если отрицается вывод, то возникает противоречие самому себе в том смысле, что отрицаются также и посылки, либо одна из них.
1)Скажи, дружище Хью, - сказал старый рыцарь, обращаясь к хозяину таверны, - тебе знаком силлогизм, где первая посылка звучит так: «Каждый орел умеет летать», а вторая так: «Некоторые свиньи не умеют летать»? - Ха-ха-ха! Вы меня, очевидно, принимаете за круглого дурака. Каждый сопливый мальчишка в нашей деревне знает вывод этого силлогизма, который звучит так:
2.Все кошки любят рыбу. Ни один слон не любит рыбу.
3.Ни одна птица – не собака. Все таксы – собаки.
4. Некоторые кошки – полосатые. Некоторые собаки – кусучие.
5. Все бабочки умеют летать. Некоторые животные – бабочки.
6. Ни один жираф не питается рыбой. Ни один жираф не синий.
7. Некоторые мыши – белые. Все мыши имеют усы.
8. Все ежики колючие. Некоторые ежики не живут в лесу.
9.Все тигры – хищники. Все тигры пушистые.
10. Ни один пингвин не живет в Африке. Некоторые птицы – пингвины.
11. Некоторые коты рыжие. Некоторые коты полосатые.
Исследование, описанное в статье про силлогизм, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое силлогизм, простой категорический силлогизм, категорический силлогизм, теория силлогизмов аристотеля, модусы силлогизма, фигуры силлогизма и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Логика
Комментарии
Оставить комментарий
Логика
Термины: Логика