Лекция
Сразу хочу сказать, что здесь никакой воды про математическая модель, и только нужная информация. Для того чтобы лучше понимать что такое математическая модель , настоятельно рекомендую прочитать все из категории Моделирование и Моделирование систем.
математическая модель — математическое представление реальности , один из вариантов модели, как системы, исследование которой позволяет получатьинформацию о некоторой другой системе. Математическая модель — это абстрактное представление реальной системы, процесса или явления с использованием математических понятий, уравнений, функций и других математических объектов. Она позволяет описывать, анализировать и предсказывать поведение и свойства интересующей системы. Математические модели используются в различных областях науки, инженерии, экономике, биологии и других дисциплинах для более глубокого понимания сложных процессов и принятия обоснованных решений.
Процесс построения и изучения математических моделей называется математическим моделированием.
Все естественные и общественные науки, использующие математический аппарат, по сути занимаются математическим моделированием: заменяют объект исследования его математической моделью и затем изучают последнюю. Связь математической модели с реальностью осуществляется с помощью цепочки гипотез,идеализаций и упрощений. С помощью математических методов описывается, как правило, идеальный объект, построенный на этапе содержательного моделирования.
Математическая модель есть приближенное описание объекта (явления, процесса), выраженное с помощью математической символики. Общую схему математического моделирования можно представить в виде, представленном на рис.1.3.
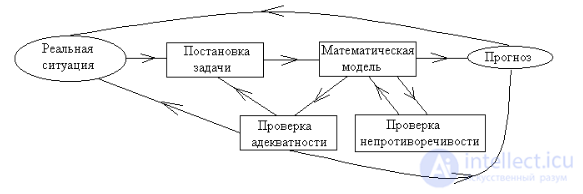
Рис.1.3. Общая схема математического моделирования
Никакое определение не может в полном объеме охватить реально существующую деятельность по математическому моделированию. Несмотря на это, определения полезны тем, что в них делается попытка выделить наиболее существенные черты.
По Ляпунову, математическое моделирование — это опосредованное практическое или теоретическое исследование объекта, при котором непосредственно изучается не сам интересующий нас объект, а некоторая вспомогательная искусственная или естественная система (модель), находящаяся в некотором объективном соответствии с познаваемым объектом, способная замещать его в определенных отношениях и дающая при ее исследовании, в конечном счете, информацию о самом моделируемом объекте .
В других вариантах, математическая модель определяется как объект-заместитель объекта-оригинала, обеспечивающий изучение некоторых свойств оригинала , как «„эквивалент“ объекта, отражающий в математической форме важнейшие его свойства — законы, которым он подчиняется, связи, присущие составляющим его частям» , как систему уравнений, или арифметических соотношений, или геометрических фигур, или комбинацию того и другого, исследование которых средствами математики должно ответить на поставленные вопросы о свойствах некоторой совокупности свойств объекта реального мира , как совокупность математических соотношений, уравнений, неравенств, описывающих основные закономерности, присущие изучаемому процессу, объекту или системе .

В общем случае математическая модель реальной системы представляется в виде системы функционалов:
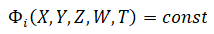 (5.1)
(5.1)
где X(Х1, …, Хk) – группа управляемых (входных переменных) факторов, которыми исследователь может управлять в процессе подготовки и проведения эксперимента;
W(W1, …, Wq) – неконтролируемые факторы (внешних воздействий), которые объективно существуют и влияют на процесс, но не известны исследователю;
Ŷ(Ŷ1, …, Ŷp) – множество выходных функций (выходных переменных), представляет собой совокупность критериальных функций;
T – координата времени.
Схема обобщенной математической модели представлена на рисунке 5.1.
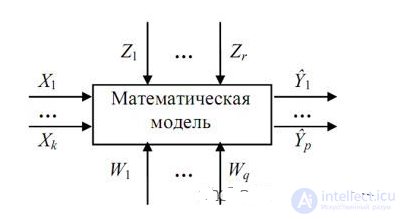
Рисунок 5.1 – Схема обобщенной математической модели
Моделирование на основе эксперимента происходит при попытке выявления зависимостей результатов экспериментальных исследований от наиболее существенных факторов исследуемой проблемы. Это позволяет обобщить результат исследований в виде некоторых математических зависимостей.
Математическое описание составляется следующим образом:
Достоинства: простота описания, доступность получения моделей, возможность построения математической модели при отсутствии теоретических данных о исследуемых процессах системы.
Недостатки: невозможность применения модели для режимов, в которых не проводились измерения, сложность или невозможность экстраполяции результатов.
Формальная классификация моделей основывается на классификации используемых математических средств. Часто строится в форме дихотомий. Например, один из популярных наборов дихотомий :
и так далее. Каждая построенная модель является линейной или нелинейной, детерминированной или стохастической, … Естественно, что возможны и смешанные типы: в одном отношении сосредоточенные (по части параметров), в другом — распределенные модели и т. д.
Наряду с формальной классификацией, модели различаются по способу представления объекта:
Структурные модели представляют объект как систему со своим устройством и механизмом функционирования. Функциональные модели не используют таких представлений и отражают только внешне воспринимаемое поведение (функционирование) объекта. В их предельном выражении они называются также моделями«черного ящика». Возможны также комбинированные типы моделей, которые иногда называют моделями «серого ящика».
Практически все авторы, описывающие процесс математического моделирования, указывают, что сначала строится особая идеальная конструкция, содержательная модель . Устоявшейся терминологии здесь нет, и другие авторы называют этот идеальный объект концептуальная модель, умозрительная модель илипредмодель. При этом финальная математическая конструкция называется формальной моделью или просто математической моделью, полученной в результате формализации данной содержательной модели (предмодели). Построение содержательной модели может производиться с помощью набора готовых идеализаций, как в механике, где идеальные пружины, твердые тела, идеальные маятники, упругие среды и т. п. дают готовые структурные элементы для содержательного моделирования. Однако в областях знания, где не существует полностью завершенных формализованных теорий (передний край физики, биологии, экономики,социологии, психологии, и большинства других областей), создание содержательных моделей резко усложняется.
В работе Пайерлса дана классификация математических моделей, используемых в физике и, шире, в естественных науках. В книге А. Н. Горбаня и Р. Г. Хлебопроса эта классификация проанализирована и расширена. Эта классификация сфокусирована, в первую очередь, на этапе построения содержательной модели.
Модели первого типа — гипотезы («такое могло бы быть»), «представляют собой пробное описание явления, причем автор либо верит в его возможность, либо считает даже его истинным». По Пайерлсу это, например, модель Солнечной системы по Птолемею и модель Коперника (усовершенствованная Кеплером), модель атома Резерфорда и модель Большого Взрыва.
Модели-гипотезы в науке не могут быть доказаны раз и навсегда, можно лишь говорить об их опровержении или неопровержении в результате эксперимента.
Если модель первого типа построена, то это означает, что она временно признается за истину и можно сконцентрироваться на других проблемах. Однако это не может быть точкой в исследованиях, но только вре́менной паузой: статус модели первого типа может быть только вре́менным.
Второй тип — феноменологическая модель («ведем себя так, как если бы…»), содержит механизм для описания явления, хотя этот механизм недостаточно убедителен, не может быть достаточно подтвержден имеющимися данными или плохо согласуется с имеющимися теориями и накопленным знанием об объекте. Поэтому феноменологические модели имеют статус вре́менных решений. Считается, что ответ все еще неизвестен, и необходимо продолжить поиск «истинных механизмов». Ко второму типу Пайерлс относит, например, модели теплорода и кварковую модель элементарных частиц.
Роль модели в исследовании может меняться со временем, может случиться так, что новые данные и теории подтвердят феноменологические модели и те будут повышены до статуса гипотезы. Аналогично новое знание может постепенно прийти в противоречие с моделями-гипотезами первого типа, и те могут быть переведены во второй. Так, кварковая модель постепенно переходит в разряд гипотез; атомизм в физике возник как временное решение, но с ходом истории перешел в первый тип. А вот модели эфира проделали путь от типа 1 к типу 2, а сейчас находятся вне науки.
Идея упрощения очень популярна при построении моделей. Но упрощение бывает разным. Пайерлс выделяет три типа упрощений в моделировании.
Третий тип моделей — приближения («что-то считаем очень большим или очень малым»). Если можно построить уравнения, описывающие исследуемую систему, то это не значит, что их можно решить даже с помощью компьютера. Общепринятый прием в этом случае — использование приближений (моделей типа 3). Среди нихмодели линейного отклика. Уравнения заменяются линейными. Стандартный пример — закон Ома.
Если мы используем модель идеального газа для описания достаточно разреженных газов, то это — модель типа 3 (приближение). При более высоких плотностях газа тоже полезно представлять себе более простую ситуацию с идеальным газом для качественного понимания и оценок, но тогда это уже тип 4.
Четвертый тип — упрощение («опустим для ясности некоторые детали»), в такой отбрасываются детали, которые могут заметно и не всегда контролируемо повлиять на результат. Одни и те же уравнения могут служить моделью типа 3 (приближение) или 4 (опустим для ясности некоторые детали) — это зависит от явления, для изучения которого используется модель. Так, если модели линейного отклика применяются при отсутствии более сложных моделей (то есть не производится линеаризация нелинейных уравнений, а просто ищутся линейные уравнения, описывающие объект), то это уже феноменологические линейные модели, и относятся они к следующему типу 4 (все нелинейные детали «для ясности» опускаем).
Примеры: применение модели идеального газа к неидеальному, уравнение состояния Ван-дер-Ваальса, большинство моделей физики твердого тела, жидкостей иядерной физики. Путь от микроописания к свойствам тел (или сред), состоящих из большого числа частиц, очень длинен. Приходится отбрасывать многие детали. Это приводит к моделям четвертого типа.
Пятый тип — эвристическая модель («количественного подтверждения нет, но модель способствует более глубокому проникновению в суть дела»), такая модель сохраняет лишь качественное подобие реальности и дает предсказания только «по порядку величины». Типичный пример — приближение средней длины свободного пробега в кинетической теории. Оно дает простые формулы для коэффициентов вязкости, диффузии, теплопроводности, согласующиеся с реальностью по порядку величины.
Но при построении новой физики далеко не сразу получается модель, дающая хотя бы качественное описание объекта — модель пятого типа. В этом случае часто используют модель по аналогии, отражающую действительность хоть в какой-нибудь черте.
Тип шестой — модель-аналогия («учтем только некоторые особенности»). Об этом говорит сайт https://intellect.icu . Пайерлс приводит историю использования аналогий в первой статье Гейзенберга о природе ядерных сил.
Седьмой тип моделей — мысленный эксперимент («главное состоит в опровержении возможности»). Такой тип моделирования часто использовался Эйнштейном, в частности, один из таких экспериментов привел к построению специальной специальной теории относительности. Предположим, что в классической физике мы движемся за световой волной со скоростью света. Мы будем наблюдать периодически меняющееся в пространстве и постоянное во времени электромагнитное поле. Согласно уравнениям Максвелла, этого быть не может. Отсюда Эйнштейн заключил: либо законы природы меняются при смене системы отсчета, либо скорость светане зависит от системы отсчета, и выбрал второй вариант.
Восьмой тип — демонстрация возможности («главное — показать внутреннюю непротиворечивость возможности»), такого рода модели тоже мысленные эксперименты с воображаемыми сущностями, демонстрирующие, что предполагаемое явление согласуется с базовыми принципами и внутренне непротиворечиво. В этом основное отличие от моделей типа 7, которые вскрывают скрытые противоречия.
Один из самых знаменитых таких экспериментов — геометрия Лобачевского. (Лобачевский называл ее «воображаемой геометрией».) Другой пример — массовое производство формально—кинетических моделей химических и биологических колебаний, автоволн. Парадокс Эйнштейна — Подольского — Розена был задуман как мысленный эксперимент для демонстрации противоречивости квантовой механики, но незапланированным образом со временем превратился в модель 8 типа — демонстрацию возможности квантовой телепортации информации.
В основе содержательной классификации — этапы, предшествующие математическому анализу и вычислениям. Восемь типов моделей по Пайерлсу суть восемь типов исследовательских позиций при моделировании.
В зависимости от характера изучаемых процессов в системе математические модели бывают:
Физические модели: описывают реальные физические процессы и системы, например, движение тела под действием сил.
Основными требованиями, предъявляемыми к математическим моделям, являются требования адекватности, непротиворечивости, универсальности и экономичности.
Модель считается адекватной, если она отражает заданные свойства объекта с приемлемой точностью.
Непротиворечивость модели заключается в том, что она не должна содержать зависимостей, которые бы противоречили друг другу.
Универсальность модели состоит в том, что она служит математическим описанием для целого класса (близких или далеких по характеру) задач. Например, дифференциальные уравнения являются математическими моделями для колебаний математического маятника, описывают колебательные процессы в механической и электрической системах, описывают колебания арки моста, процессы, протекающие в струнах музыкальных инструментов, и т.д. Универсальность определяется также числом и составом учитываемых в модели входных и выходных параметров.
Экономичность модели характеризуется затратами вычислительных ресурсов для ее реализации, а именно, затратами машинного времени и памяти. Эти затраты зависят как от особенностей выбранной модели, так и от методов решения соответствующих математических задач.
Требования адекватности и универсальности, с одной стороны, и высокой экономичности, с другой, очевидно, являются противоречивыми. Поэтому для удовлетворения всем указанным требованиям разработчик модели должен идти на компромисс.
Вот некоторые дополнительные требования, предъявляемых к математическим моделям:
Модель должна быть достаточно простой, чтобы ее можно было анализировать и интерпретировать. Слишком сложные модели могут быть трудными в понимании и использовании.
Предсказательная способность: Модель должна обладать способностью делать предсказания о поведении системы в будущем. Это важно для использования модели в прогнозировании и планировании.
Устойчивость: Модель должна сохранять свои характеристики и результаты при небольших изменениях входных данных или параметров.
Проверяемость: Модель должна быть поддающейся проверке на основе экспериментов, наблюдений или других методов. Это помогает убедиться в соответствии модели реальным данным.
Объяснимость: Модель должна быть понятной и интерпретируемой. Способность объяснить, какие факторы и взаимодействия приводят к определенным результатам, делает модель более полезной.
Общность: Желательно, чтобы модель имела способность применяться не только к конкретной ситуации, но и к широкому классу подобных проблем.
Соответствие целям: Модель должна быть разработана с учетом конкретных целей и задач, которые необходимо решить.
Подтверждение экспериментальными данными: Модель должна быть проверена и подтверждена реальными экспериментальными данными или наблюдениями, чтобы убедиться в ее точности.
Ресурсоэффективность: Модель должна быть вычислительно эффективной и способной работать с доступными ресурсами (временем, вычислительной мощностью и т.д.).
Адаптируемость: Модель должна быть гибкой и способной быть адаптированной к изменениям в системе или новым данным.
Реалистичность предположений: Модель должна основываться на реалистичных и обоснованных предположениях о системе.
Требования к моделям могут меняться в зависимости от конкретной области применения и целей моделирования.
Рассмотрим механическую систему, состоящую из пружины, закрепленной с одного конца, и груза массой  , прикрепленного к свободному концу пружины. Будем считать, что груз может двигаться только в направлении оси пружины (например, движение происходит вдоль стержня). Построим математическую модель этой системы. Будем описывать состояние системы расстоянием
, прикрепленного к свободному концу пружины. Будем считать, что груз может двигаться только в направлении оси пружины (например, движение происходит вдоль стержня). Построим математическую модель этой системы. Будем описывать состояние системы расстоянием 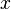 от центра груза до его положения равновесия. Опишем взаимодействие пружины и груза с помощью закона Гука (
от центра груза до его положения равновесия. Опишем взаимодействие пружины и груза с помощью закона Гука (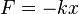 ), после чего воспользуемся вторым законом Ньютона, чтобы выразить его в форме дифференциального уравнения:
), после чего воспользуемся вторым законом Ньютона, чтобы выразить его в форме дифференциального уравнения:
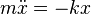 ,
,
где 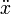 означает вторую производную от
означает вторую производную от 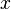 по времени:
по времени: 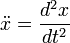 .
.
Полученное уравнение описывает математическую модель рассмотренной физической системы. Эта модель называется «гармоническим осциллятором».
По формальной классификации эта модель линейная, детерминистская, динамическая, сосредоточенная, непрерывная. В процессе ее построения мы сделали множество допущений (об отсутствии внешних сил, отсутствии трения, малости отклонений и т. д.), которые в реальности могут не выполняться.
По отношению к реальности это, чаще всего, модель типа 4 упрощение («опустим для ясности некоторые детали»), поскольку опущены некоторые существенные универсальные особенности (например, диссипация). В некотором приближении (скажем, пока отклонение груза от равновесия невелико, при малом трении, в течение не слишком большого времени и при соблюдении некоторых других условий), такая модель достаточно хорошо описывает реальную механическую систему, поскольку отброшенные факторы оказывают пренебрежимо малое влияние на ее поведение. Однако модель можно уточнить, приняв во внимание какие-то из этих факторов. Это приведет к новой модели, с более широкой (хотя и снова ограниченной) областью применимости.
Впрочем, при уточнении модели сложность ее математического исследования может существенно возрасти и сделать модель фактически бесполезной. Зачастую более простая модель позволяет лучше и глубже исследовать реальную систему, чем более сложная (и, формально, «более правильная»).
Если применять модель гармонического осциллятора к объектам, далеким от физики, ее содержательный статус может быть другим. Например, при приложении этой модели к биологическим популяциям ее следует отнести, скорее всего, к типу 6 аналогия («учтем только некоторые особенности»).
Гармонический осциллятор — пример так называемой «жесткой» модели. Она получена в результате сильной идеализации реальной физической системы. Свойства гармонического осциллятора качественно изменяются малыми возмущениями. Например, если добавить в правую часть малое слагаемое 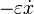 (трение) (
(трение) (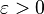 — некоторый малый параметр), то получим экспоненциально затухающие колебания, если изменить знак добавочного слагаемого
— некоторый малый параметр), то получим экспоненциально затухающие колебания, если изменить знак добавочного слагаемого 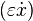 то трение превратится в накачку и амплитуда колебаний будет экспоненциально возрастать.
то трение превратится в накачку и амплитуда колебаний будет экспоненциально возрастать.
Для решения вопроса о применимости жесткой модели необходимо понять, насколько существенными являются факторы, которыми мы пренебрегли. Нужно исследовать мягкие модели, получающиеся малым возмущением жесткой. Для гармонического осциллятора они могут задаваться, например, следующим уравнением:
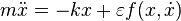 .
.
Здесь 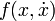 — некоторая функция, в которой может учитываться сила трения или зависимость коэффициента жесткости пружины от степени ее растяжения. Явный вид функции
— некоторая функция, в которой может учитываться сила трения или зависимость коэффициента жесткости пружины от степени ее растяжения. Явный вид функции 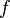 нас в данный момент не интересует.
нас в данный момент не интересует.
Если мы докажем, что поведение мягкой модели принципиально не отличается от поведения жесткой (вне зависимости от явного вида возмущающих факторов, если они достаточно малы), задача сведется к исследованию жесткой модели. В противном случае применение результатов, полученных при изучении жесткой модели, потребует дополнительных исследований.
Если система сохраняет свое качественное поведение при малом возмущении, говорят, что она структурно устойчива. Гармонический осциллятор — пример структурно-неустойчивой (негрубой) системы. Тем не менее, эту модель можно применять для изучения процессов на ограниченных промежутках времени.
Важнейшие математические модели обычно обладают важным свойством универсальности: принципиально разные реальные явления могут описываться одной и той же математической моделью. Скажем, гармонический осциллятор описывает не только поведение груза на пружине, но и другие колебательные процессы, зачастую имеющие совершенно иную природу: малые колебания маятника, колебания уровня жидкости в 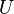 -образном сосуде или изменение силы тока в колебательном контуре. Таким образом, изучая одну математическую модель, мы изучаем сразу целый класс описываемых ею явлений. Именно этот изоморфизм законов, выражаемых математическими моделями в различных сегментах научного знания, подвиг Людвига фон Берталанфи на создание «общей теории систем».
-образном сосуде или изменение силы тока в колебательном контуре. Таким образом, изучая одну математическую модель, мы изучаем сразу целый класс описываемых ею явлений. Именно этот изоморфизм законов, выражаемых математическими моделями в различных сегментах научного знания, подвиг Людвига фон Берталанфи на создание «общей теории систем».
Существует множество задач, связанных с математическим моделированием. Во-первых, надо придумать основную схему моделируемого объекта, воспроизвести его в рамках идеализаций данной науки. Так, вагон поезда превращается в систему пластин и более сложных тел из разных материалов, каждый материал задается как его стандартная механическая идеализация (плотность, модули упругости, стандартные прочностные характеристики), после чего составляются уравнения, по дороге какие-то детали отбрасываются как несущественные, производятся расчеты, сравниваются с измерениями, модель уточняется, и так далее. Однако для разработки технологий математического моделирования полезно разобрать этот процесс на основные составные элементы.
Традиционно выделяют два основных класса задач, связанных с математическими моделями: прямые и обратные.
Прямая задача: структура модели и все ее параметры считаются известными, главная задача — провести исследование модели для извлечения полезного знания об объекте. Какую статическую нагрузку выдержит мост? Как он будет реагировать на динамическую нагрузку (например, на марш роты солдат, или на прохождение поезда на различной скорости), как самолет преодолеет звуковой барьер, не развалится ли он от флаттера, — вот типичные примеры прямой задачи. Постановка правильной прямой задачи (задание правильного вопроса) требует специального мастерства. Если не заданы правильные вопросы, то мост может обрушиться, даже если была построена хорошая модель для его поведения. Так, в 1879 г. в Великобритании обрушился металлический железнодорожный мост через реку Тей, конструкторы которого построили модель моста, рассчитали его на 20-кратный запас прочности на действие полезной нагрузки, но забыли о постоянно дующих в тех местах ветрах. И через полтора года он рухнул.
В простейшем случае (одно уравнение осциллятора, например) прямая задача очень проста и сводится к явному решению этого уравнения.
Обратная задача: известно множество возможных моделей, надо выбрать конкретную модель на основании дополнительных данных об объекте. Чаще всего структура модели известна, и необходимо определить некоторые неизвестные параметры. Дополнительная информация может состоять в дополнительных эмпирических данных, или в требованиях к объекту (задача проектирования). Дополнительные данные могут поступать независимо от процесса решения обратной задачи (пассивное наблюдение) или быть результатом специально планируемого в ходе решения эксперимента (активное наблюдение).
Одним из первых примеров виртуозного решения обратной задачи с максимально полным использованием доступных данных был построенный Ньютоном метод восстановления сил трения по наблюдаемым затухающим колебаниям.
В качестве другого примера можно привести математическую статистику. Задача этой науки — разработка методов регистрации, описания и анализа данных наблюдений и экспериментов с целью построения вероятностных моделей массовых случайных явлений. То есть множество возможных моделей ограничено вероятностными моделями. В конкретных задачах множество моделей ограничено сильнее.
Для поддержки математического моделирования разработаны системы компьютерной математики, например, Maple, Mathematica, Mathcad, MATLAB, VisSim и др.Они позволяют создавать формальные и блочные модели как простых, так и сложных процессов и устройств и легко менять параметры моделей в ходе моделирования. Блочные модели представлены блоками (чаще всего графическими), набор и соединение которых задаются диаграммой модели.
Согласно модели, предложенной Мальтусом, скорость роста пропорциональна текущему размеру популяции, то есть описывается дифференциальным уравнением:
 ,
,
где 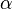 — некоторый параметр, определяемый разностью между рождаемостью и смертностью. Решением этого уравнения является экспоненциальная функция
— некоторый параметр, определяемый разностью между рождаемостью и смертностью. Решением этого уравнения является экспоненциальная функция 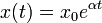 . Если рождаемость превосходит смертность (
. Если рождаемость превосходит смертность (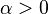 ), размер популяции неограниченно и очень быстро возрастает. В действительности этого не может происходить из-за ограниченности ресурсов. При достижении некоторого критического объема популяции модель перестает быть адекватной, поскольку не учитывает ограниченность ресурсов. Уточнением модели Мальтуса может служить логистическая модель, которая описывается дифференциальным уравнениемФерхюльста:
), размер популяции неограниченно и очень быстро возрастает. В действительности этого не может происходить из-за ограниченности ресурсов. При достижении некоторого критического объема популяции модель перестает быть адекватной, поскольку не учитывает ограниченность ресурсов. Уточнением модели Мальтуса может служить логистическая модель, которая описывается дифференциальным уравнениемФерхюльста:
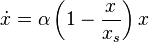 ,
,
где 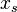 — «равновесный» размер популяции, при котором рождаемость в точности компенсируется смертностью. Размер популяции в такой модели стремится к равновесному значению
— «равновесный» размер популяции, при котором рождаемость в точности компенсируется смертностью. Размер популяции в такой модели стремится к равновесному значению 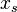 , причем такое поведение структурно устойчиво.
, причем такое поведение структурно устойчиво.
Допустим, что на некоторой территории обитают два вида животных: кролики (питающиеся растениями) и лисы (питающиеся кроликами). Пусть число кроликов 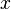 , число лис
, число лис 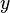 . Используя модель Мальтуса с необходимыми поправками, учитывающими поедание кроликов лисами, приходим к следующей системе, носящей имямодели Лотки — Вольтерры:
. Используя модель Мальтуса с необходимыми поправками, учитывающими поедание кроликов лисами, приходим к следующей системе, носящей имямодели Лотки — Вольтерры:
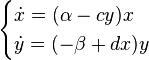
Эта система имеет равновесное состояние, когда число кроликов и лис постоянно. Отклонение от этого состояния приводит к колебаниям численности кроликов и лис, аналогичным колебаниям гармонического осциллятора. Как и в случае гармонического осциллятора, это поведение не является структурно устойчивым: малое изменение модели (например, учитывающее ограниченность ресурсов, необходимых кроликам) может привести к качественному изменению поведения. Например, равновесное состояние может стать устойчивым, и колебания численности будут затухать. Возможна и противоположная ситуация, когда любое малое отклонение от положения равновесия приведет к катастрофическим последствиям, вплоть до полного вымирания одного из видов. На вопрос о том, какой из этих сценариев реализуется, модель Вольтерры — Лотки ответа не дает: здесь требуются дополнительные исследования.
Эффективность экспериментальных исследований сложных систем оказывается крайне низкой, поскольку проведение натурных экспериментов с реальной системой либо требует больших материальных затрат и значительного времени, либо вообще практически невозможно, например, на этапе проектирования, когда реальная система отсутствует.
Появление современных ЭВМ явилось решающим условием широкого внедрения методов математического моделирования в исследование сложных систем вообще, и информационных систем, в частности. Математические модели и аналитические методы их исследования могут решить многие проблемы, определяющие качество функционирования сложных систем. Однако, одновременно с этим появились причины, препятствующие применению в инженерной практике аналитических методов исследования систем:
Это приводит к необходимости разработки более адекватных математических моделей. С этой целью шире стали применяться методы имитационного моделирования.
Современные ЭВМ можно разделить на две группы: универсальные, предназначенные для выполнения расчетных работ и управляющие, предназначенные, прежде всего, для управления объектами в реальном масштабе времени. Управляющие ЭВМ могут быть использованы как для управления технологическими процессами, так и для реализации имитационных моделей. Эксперимент с имитационной моделью требует серьезной подготовки [25], поэтому имитационная модель характеризуется наличием математического, программного, информационного, технического и других видов обеспечения.
Математическое обеспечение имитационных моделей включает в себя совокупность математических соотношений, описывающих поведение реального объекта, совокупность алгоритмов, обеспечивающих работу с моделью: алгоритмы ввода исходных данных, имитации, вывода, обработки.
Программное обеспечение включает в себя совокупность программ: планирования эксперимента, имитационной модели, проведения эксперимента, обработки и интерпретации результатов.
Информационное обеспечение включает в себя средства и технологию организации и реорганизации базы данных моделирования, формы документов, описывающих процесс моделирования и его результаты.
Техническое обеспечение имитационной модели включает в себя средства вычислительной техники, связи и диалоговую систему обмена между оператором и ЭВМ, ввода и вывода информации, управления проведением эксперимента.
Таким, образом, имитационная система может рассматриваться как машинный аналог сложного реального процесса. Он позволяет заменить эксперимент с реальным процессом функционирования системы экспериментом с математической моделью этого процесса в компьютере.
Имитационное моделирование на компьютере имеет достоинства и недостатки, проявляющиеся в конкретных приложениях. Основные достоинства:
Основным недостатком имитационного моделирования на компьютере является то, что решение, полученное при анализе имитационной модели, всегда носит частный характер. Поэтому для полного анализа характеристик процесса функционирования системы приходится многократно воспроизводить имитационный эксперимент, варьируя исходные данные задачи. При этом, как следствие, возникает увеличение затрат машинного времени на проведение эксперимента с имитационной моделью. Эффективность имитационного моделирования может оцениваться рядом критериев, в том числе точностью и достоверностью результатов моделирования, временем построения и работы с моделью, затратами машинных ресурсов (времени и памяти), стоимостью разработки и эксплуатации модели.
Специалисты в области проектирования, исследования и эксплуатации больших систем должны в совершенстве знать методологию машинного моделирования, сложившуюся к настоящему времени, чтобы быть готовыми к появлению компьютера следующих поколений, которые позволят сделать следующие шаги в направлении автоматизации построения моделей и использования имитационного моделирования систем.
Информационные системы представляют собой сложные территориально распределенные системы, в состав которых входят тысячи комплектующих элементов. Однако эти системы характеризуются не только большим числом элементов - чисто количественная сторона естественным образом перерастает в новое качество: таким системам присущи
Кроме того, эти системы, как правило, являются развивающимися, то есть в процессе своего существования они постоянно модернизируются, меняются условия их работы и выполняемые задачи.
Разработка математических моделей, адекватно описывающих процесс функционирования таких систем, оказывается весьма сложной и трудоемкой.
К построению математических моделей необходимо относиться как к искусству: нужно уметь строить достаточно простую модель, которая при этом могла бы все же приводить к конструктивным выводам об исследуемой системе. Приведем основные требования к построению математических моделей информационных систем.
1. Математическая модель должна отражать основные свойства исследуемого объекта с точки зрения интересующего параметра или группы параметров. Например, если рассматривается время доставки сообщений в системе с пакетной коммутацией, то подходящей математической моделью может быть сеть массового обслуживания с ненадежными обслуживающими устройствами (узлами коммутации, каналами связи). Если же изучается вопрос о живучести сети по отношению к различного рода внешним воздействиям, то при выборе в качестве основного показателя вероятности связности подходящей математической моделью может оказаться граф с сетевой структурой.
2. Математическая модель должна быть достаточно простой в содержательном смысле, то есть результаты ее анализа должны быть легко интерпретируемы. Это означает, что слишком подробная модель, обеспечивающая одновременное получение большого числа взаимосвязанных параметров, может и не быть наилучшим вариантом. Например, получение совместного распределения числа обслуживаемых заявок в сети связи в различных узлах коммутации может оказаться той информацией, которую исследователь не умеет принципиально использовать.
3. Математическая модель должна быть адаптированной под имеющиеся исходные данные. Например, бессмысленно строить полумарковскую модель для описания процесса функционирования системы с восстановлением, если о распределениях известны лишь значения математических ожиданий. Если при таких же исходных данных требуется оценить значения структурных параметров сети, то нужно иметь в виду, что могут быть получены лишь двусторонние оценки, а не точные значения соответствующих параметров.
4. Математическая модель должна быть легко модифицируемой при появлении новых исходных данных или новых сведений о внутренней природе системы. Например, статистическая модель системы передачи данных в режиме пакетной коммутации должна предусматривать возможность использования ее при различных протоколах верхнего уровня. Математическая модель для статистического моделирования системы связи с коммутацией сообщений должна иметь общее программное ядро с математической моделью системы связи с коммутацией каналов.
5. Математическая модель информационной системы - объекта весьма сложного и содержащего огромное число входящих в ее состав подсистем и устройств - должна быть сформулирована так, чтобы размерность этой модели позволяла бы проводить расчеты на доступной вычислительной технике в разумные сроки.
Для системы связи и передачи данных могут возникать чрезмерные задержки в передачи информации, потери сообщений, случайный рост загрузки каналов связи, отказы из-за несовершенства протоколов сетевого уровня в системах передачи данных.
Большинство сетей связи и систем передачи данных, обеспечивающих информационный обмен между большим числом территориально разнесенных абонентов, имеют очень сложную сетевую структуру. Связь между отдельными пунктами информационной сети может осуществляться по многим возможным путям, включая транзит по целому ряду пунктов. В то же время для реальных сетей имеются и различные сложные ограничения, например, допускается не более заданного числа транзитов. Однако самым важным является то, что передача сообщения в сети занимает на определенное время те или иные канальные мощности, а также процессоры в узлах связи. Поэтому более или менее адекватная модель сети связи - это сеть массового обслуживания. Более грубо сеть может быть описана при помощи потоковой модели. Чаще всего для получения различных характеристик эффективности функционирования сетей связи используются статистические модели, реализуемые на современных быстродействующих компьютеров.
А как ты думаешь, при улучшении математическая модель, будет лучше нам? Надеюсь, что теперь ты понял что такое математическая модель и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Моделирование и Моделирование систем
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Моделирование и Моделирование систем
Термины: Моделирование и Моделирование систем