ГЛАВА 11. МЕТОДЫ ТЕОРЕТИЧЕСКОГО И ЭМПИРИЧЕСКОГО ИССЛЕДОВАНИЯ 11.1. Методы теоретического исследования кратко

Привет, Вы узнаете о том , что такое методы теоретического, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое методы теоретического, эмпирического исследования методы теоретического исследования , настоятельно рекомендую прочитать все из категории ОСНОВЫ НАУЧНЫХ ИССЛЕДОВАНИЙ и организация научно-исследовательской деятельности.

 ВВЕДЕНИЕ В ГЛАВУ
202
202
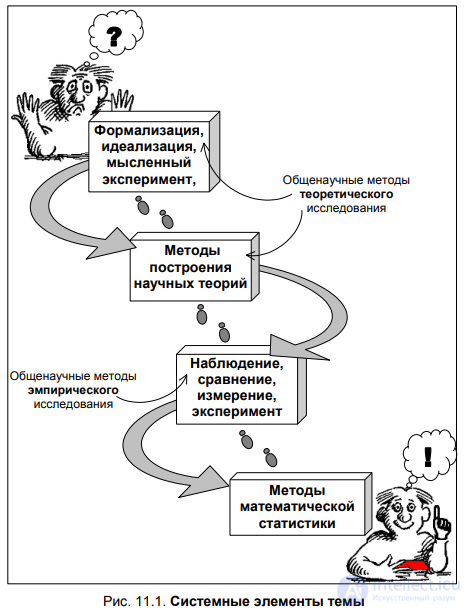
Цель данной главы – описать две группы общенаучных методов –
методы теоретического и методы эмпирического исследования.
В этой главе мы ответим на следующие вопросы: Использование
каких методов характерно для теоретического исследования? С помощью каких методов строятся научные теории? Какие методы типичны
для эмпирических исследований? Чем эксперимент отличается от
наблюдения, а измерение от сравнения?
Кроме этого в практической компоненте главы мы рассмотрим методы одной из наук (математической статистики), предназначенные для
обработки больших массивов эмпирических данных.
Ключевые понятия данной главы: формализация, идеализация,
мысленный эксперимент, метод восхождения от абстрактного к конкретному, аксиоматический метод, гипотетико-дедуктивный метод, наблюдение, сравнение, измерение, эксперимент, методы математической статистики, коэффициент парной корреляции.
.
 ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ
§ 11.1. Методы теоретического исследования
Напомним, что теоретическое исследование – это исследование,
направленное на объяснение сущности связей в исследуемых объектах,
на вскрытие внутреннего механизма явлений (см. главу 3).
К общенаучным методам теоретического исследования относят
методы построения научных теорий (аксиоматический и гипотетикодедуктивный методы), а также формализацию, идеализацию, мысленный эксперимент и метод восхождения от абстрактного к конкретному
[15]. Рассмотрим кратко эти методы.
 Формализация – это отображение объектов предметной области в формализованном языке в виде стойких точных понятий и
утверждений, символов и формул. При этом дальнейшее исследование
ведется «формально», то есть путем преобразования одних формул
(утверждений, символов) в другие.
Формальное описание объектов предметной области позволяет исключить неопределенность и неоднозначность естественных язы-
203
203
ков. Особенно широко формализация применяется в математике.
 Идеализация – это мысленное конструирование идеализированных объектов, не существующих в действительности или практически неосуществимых.
Примерами идеальных объектов являются: в физике - абсолютно
черное тело, идеальный газ; в механике – абсолютно жесткое тело, идеально пластичное тело; в математике – линия, плоскость, точка, окружность; в экономике – экономический человек, полная рациональность в
принятии решений.
Идеализация может быть осуществлена с помощью метода абстрагирования (например, абстрагирование от толщины приводит к понятию плоскости), а также мысленным переходом к предельному случаю
в развитии какого-либо свойства (так, например, было сформировано
понятие абсолютно твердого тела).
 Мысленный эксперимент – это один из важнейших познавательных приемов теоретического мышления, суть которого заключается в том, что с помощью одного лишь воображения объект исследования рассматривается в «чистом виде», независимо от конкретной формы его взаимодействия с окружающей средой.
Мысленный эксперимент осуществляется на основе абстракции и
идеализации. Об этом говорит сайт https://intellect.icu . Мысленный эксперимент с идеализированными объектами как бы замещает реальный эксперимент с реальными объектами.
 Метод восхождения от абстрактного к конкретному –
это метод теоретического исследования, заключающийся в том, что
после перехода от конкретного объекта к его абстрактному описанию и исследования полученной абстракции, осуществляется обратный переход от абстрактного к конкретному, когда объект воспроизводится в своей целостности и многогранности – но уже в мышлении.
Метод восхождения от абстрактного к конкретному применяется
при построении научных теорий. Например, при построении теории организации исследователь формулирует основные принципы создания
организационных структур, а затем переходит к изучению того, как
204
204
сформулированные принципы проявляются в различных экономических
системах.
К методам построения научных теорий также относятся гипотетикодедуктивный и аксиоматический методы [54].
 Гипотетико-дедуктивный метод состоит в выдвижении
некоторых гипотез и дальнейшей проверке этих гипотез путем вывода из них следствий и сопоставления этих следствий с фактами. В
гипотетико-дедуктивном методе в качестве посылки выступают гипотезы, а следствия из гипотез выводятся методом дедукции.
Гипотетико-дедуктивный метод является специфическим методом
построения научной теории в эмпирических науках, то есть в тех науках,
где в отличие от математики и логики теория должна быть не только
внутренне непротиворечивой, но и соответствовать фактам природного
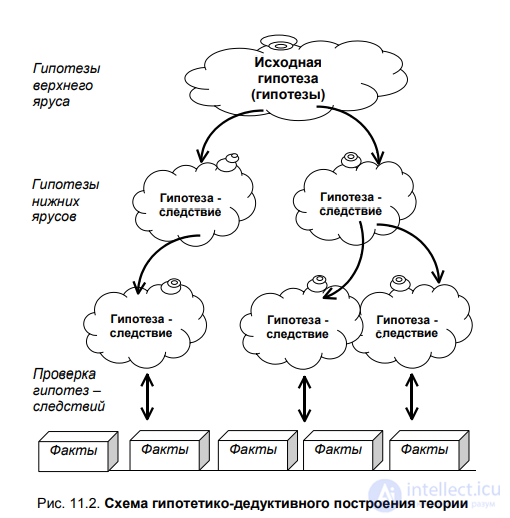
мира. Сущность гипотетико-дедуктивного построения теории состоит в
том, что сначала формулируется исходная гипотеза, а затем посредством дедуктивных умозаключений из этой гипотезы выводятся следствия, которые далее подвергаются опытной проверке (рис. 11.2). Как
видим, при гипотетико-дедуктивном методе теория строится не «снизувверх» – от научных фактов к индуктивным обобщениям и теоретическим выводам, а «сверху-вниз» – от исходных гипотез к их следствиям и
далее к эмпирическим данным. Причиной широкого распространения гипотетико-дедуктивного метода является тот факт, что возможность
непосредственной проверки гипотетического предположения в науке
встречается достаточно редко. Например, для того, чтобы проверить гипотезу о том, что во времена первобытнообщинного строя уже существовал прообраз современных денег, нужно было бы перенестись во
времени на многие тысячелетия назад, что пока невозможно.
П
Пример 11.1
Проверка следствий из теории относительности

Одним из следствий, выведенных на основе общей теории относительности Эйнштейна, являлось положение о том, что эллипсы, по которым планеты обращаются вокруг Солнца, также медленно поворачиваются относительно светила. Частный случай этого положения –
утверждение о вращении Меркурия было подтверждено астрономами.
Кстати, это явление было открыто задолго до Эйнштейна, но объяснения ему долго не находилось. Доказательство истинности одного из
следствий теории относительности было расценено как свидетельство в
пользу истинности самой теории.

Аксиоматический метод — это метод теоретического исследования, основанный на том, что ряд очевидных положений (аксиом) принимается без доказательства. При этом аксиомы выступают
посылками умозаключений, а следствия из них формируются чисто
логическим путем на основе принципа дедукции. Широкое распространение аксиоматический метод получил в математике.
 Аксиома – это положение, не требующие доказательства
истинности.
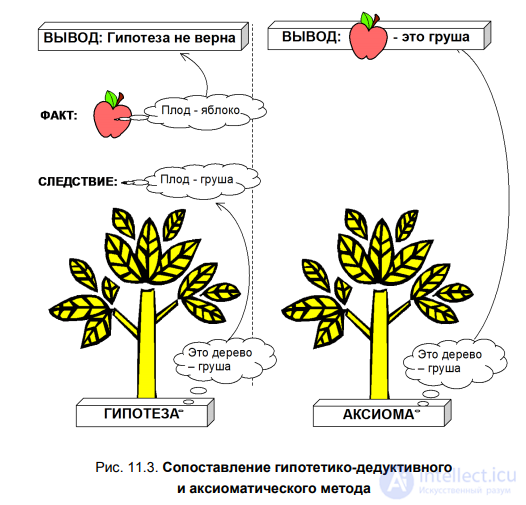
Аксиоматическое построение теории осуществляется следующим
образом (рис. 11.3):
1. Сначала задается набор исходных положений, не требующих
доказательства (в рамках данной системы знания). Эти положения
называются аксиомами или постулатами.
2. Затем задаются правила формирования следствий из аксиом.
3. Наконец, из аксиом в соответствии с заданными правилами строится система выводов. Совокупность исходных аксиом и выведенных на их
основе положений образует аксиоматически построенную теорию.
Выделяют три разновидности аксиоматического подхода: содержательно-аксиоматический, формальный и формализованный.
При содержательно-аксиоматическом построении теории в качестве аксиом выступают интуитивно очевидные положения. Широко известным примером содержательно-аксиоматической теории является
геометрия Евклида. Аналогичный подход применен и при построении
экономической теории ожидаемой полезности – данная теория базируется на аксиоме о том, что человек принимает экономические решения,
исходя из стремления максимизировать предполагаемую выгоду.
При формальном построении аксиоматической системы аксиомы
вводятся формально, к ним не предъявляется требование интуитивной
очевидности, они рассматриваются как своеобразные определения исходных понятий (терминов) создаваемой системы (Пример 11.2).
Особенностью формализованного построения аксиоматической
системы является использование математической логики как средства,

обеспечивающего строгие правила вывода следствий из доказанных
утверждений. При построении формализованной аксиоматической системы вводятся исходные знаки - термины, определяются правила их
соединения в формулы, задается перечень исходных формул (принимаемых без доказательства) и правила вывода формул-следствий.
Обычная алгебра, которую учат в школе, не единственно
возможная... Можно определить понятия сложения и умножения
объектов и при этом отказаться от аксиом обычной алгебры,
например от предположения, что результат умножения не зависит от порядка сомножителей. Получится другая алгебра
(А. Мигдал [26]).

Пример 11.2
Геометрия Лобачевского
Примером формальной аксиоматической системы является геометрия Н. И. Лобачевского. Данная геометрическая теория основывается на тех же аксиомах, что и геометрия Евклида, за исключением аксиомы о параллельных прямых. Евклидова аксиома о параллельных прямых (в плоскости через точку, не лежащую на данной прямой, можно
провести одну, и только одну, прямую, параллельную данной) заменена

в геометрии Лобачевского следующей формальной аксиомой: в плоскости через точку, не лежащую на данной прямой, можно провести более
одной прямой, не пересекающей данную. Следствием этого изменения
стало то, что в геометрии Лобачевского многие теоремы отличаются от
соответствующих теорем евклидовой геометрии: например, сумма углов
треугольника меньше 180 градусов. Однако при этом геометрия Лобачевского является внутренне непротиворечивой системой и логически
равноправна с евклидовой геометрией.

Исследование, описанное в статье про методы теоретического, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое методы теоретического, эмпирического исследования методы теоретического исследования и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории ОСНОВЫ НАУЧНЫХ ИССЛЕДОВАНИЙ и организация научно-исследовательской деятельности

Из статьи мы узнали кратко, но содержательно про методы теоретического

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.