8.1 Двоичные циклические коды.

Привет, сегодня поговорим про двоичные циклические коды , обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое двоичные циклические коды , настоятельно рекомендую прочитать все из категории Теория информации и кодирования.

Лекция 8.

8.1 двоичные циклические коды .

Вышеприведенная процедура построения линейного кода матричным методом имеет ряд недостатков. Она неоднозначна (МДР можно задать различным образом) и неудобна в реализации в виде технических устройств. Этих недостатков лишены линейные корректирующие коды, принадлежащие к классу циклических.

Циклическиминазывают линейные (n,k)-коды, обладающие следующим свойством: для любого кодового слова:

 

_{<![if !vml]>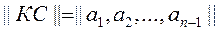<![endif]>}

 

существует другое кодовое слово:

_{<![if !vml]><![endif]>}

полученное циклическим сдвигом элементов исходного кодового слова ||КС|| вправо или влево, которое также принадлежит этому коду.

Для описания циклических кодов используют полиномы с фиктивной переменной X.

Например, пусть кодовое слово ||КС|| = ||011010||.

Его можно описать полиномом

_{<![if !vml]>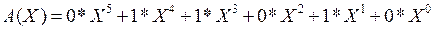<![endif]>}

Таким образом, разряды кодового слова в описывающем его полиноме используются в качестве коэффициентов при степенях фиктивной переменной X.

Наибольшая степень фиктивной переменной Xв слагаемом с ненулевым коэффициентом называется степенью полинома. В вышеприведенном примере получился полином 4-й степени.

Теперь действия над кодовыми словами сводятся к действиям над полиномами. Вместо алгебры матриц здесь используется алгебра полиномов.

Рассмотрим алгебраические действия над полиномами, используемые в теории циклических кодов. Суммирование полиномов разберем на примере С(Х)=А(Х)+В(Х).

 

Пусть

||A|| = ||011010||, ||В|| = ||110111|.

Тогда

_{<![if !vml]>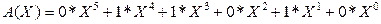<![endif]>}

_{<![if !vml]><![endif]>}

_{<![if !vml]>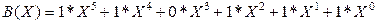<![endif]>}

---------------------------------------------------------------

_{<![if !vml]>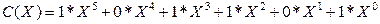<![endif]>}

 

Таким образом, при суммировании коэффициентов при X в одинаковой степени результат берется по модулю 2. При таком правиле вычитание эквивалентно суммированию.

Умножение выполняется как обычно, но с использованием суммирования по модулю 2.

Рассмотрим умножение на примере умножения полинома (X³+X¹+X⁰)

на полином X¹+X⁰

 

X³ + 0*X²+X¹+X⁰

*

X¹+X⁰

^{---------------------------------------------------}

X³+ 0*X²+X¹+Х⁰

X⁴+0*Х³+X²+Х¹

^{____________________________________}

Х⁴+X³+X²+0*X¹+X⁰

 

Операция - обратная умножению -деление. Деление полиномов выполняется как обычно, за исключением того, что вычитание выполняется по модулю 2. Вспомним, что вычитание по модулю 2 эквивалентно сложению по модулю 2

Пример деления полиномаX⁶+X⁴+X³на полином X³+X²+1

X⁶+0*X⁵+X⁴ + X³+0*X²+0*X¹+0 | X³+X²+1

X⁶+X⁵+0*X⁴ + X³результат==| X³ +X²

-----------------------------------

X⁵ +X⁴ + 0*X³+0*X²

X⁵ +X⁴ + 0*X³+X²

----------------------------------------

остаток==X² = 100

Циклический сдвиг влево на одну позицию коэффициентов полинома степени n-1получается путем его умножения на X с последующим вычитанием из результата полинома Xⁿ+1, если его порядок > п.

Проверим это на примере.

Пусть требуется выполнить циклический сдвиг влево на одну позицию

коэффициентов полинома

C(X)=X⁵+Х³+X²+1 → (101101)

В результате должен получиться полином

C₁(X)=X⁴+Х³+X¹+1 → (011011)

Это легко доказывается:

C₁(X)=C(X)*X-(X⁶+1)=(X⁶+Х⁴+X³+X)+( X⁶+1)=X⁴+Х³+X¹+1

В основе циклического кода лежит образующий полином r-гопорядка (напомним, что r- число дополнительных разрядов). Будем обозначать его g_r(X).

Образование кодовых слов (кодирование) КС выполняется путем умножения информационного полинома с коэффициентами, являющимися информационной последовательностью И(Х)порядка i<kна образующий полином g_r(X)

КС_r+k(Х)=g_r(X)+ИС_k(Х).

Принятое кодовое слово может отличаться от переданного искаженными разрядами в результате воздействия помех.

ПКС(Х)=КС(Х)+ВО(Х).

где ВО(Х) - полином вектора ошибки, а суммирование, как обычно, ведется по модулю 2.

Декодирование, как и раньше начинается с нахождения опознавателя, в данном случае в виде полинома ОП(Х). Этот полином вычисляется как остаток от деления полинома принятого кодового слова ПКС(Х) на образующий полином g(Х):

<![if !vml]>

<![endif]>

Первое слагаемое остатка не имеет, т.к. кодовое слово было образовано путем умножения полинома информационной последовательности на образующий полином. Следовательно, и в данном случае опознаватель полностью зависит от вектора ошибки.

<![if !vml]><![endif]>

Образующий полином выбирается таким, чтобы при данном rкак можно большее число отношений ВО(Х)/g(Х) давало различные остатки.

Такому требованию отвечают так называемые неприводимые полиномы, которые не делятся без остатка ни на один полином степени r и ниже, а делятся только сами на себя и на 1.

Приведенная здесь процедура образования кодового слова неудобна тем, что такой код получается несистематическим, т.е. Об этом говорит сайт https://intellect.icu . таким, в кодовых словах которого нельзя выделить информационные и дополнительные разряды.

Этот недостаток был устранен следующим образом.

Способ кодирования, приводящий к получению систематического линейного циклического кода, состоит в приписывании к информационной последовательности И дополнительных разрядов ДР.

Эти дополнительные разряды предлагается находить по следующей формуле:

<![if !vml]><![endif]>

Порядок полинома ДР(Х) гарантировано меньше r (поскольку это остаток).

Приписывание дополнительных разрядов к информационной последовательности, используя алгебру полиномов, можно описать формулой:

<![if !vml]>

<![endif]>

Одним из свойств циклических линейных кодов является то, что результат деления любого разрешенного кодового слова КС на образующий полином также, является разрешенным кодовым словом.

Покажем, что получаемые по вышеприведенному алгоритму кодовые слова являются кодовыми словами циклического линейного кода. Для этого нужно убедиться в том, что произвольное разрешенное кодовое слово делится на образующий полином g(X) без остатка:

<![if !vml]>

<![endif]>

 

Рассмотрим первое слагаемое:

<![if !vml]>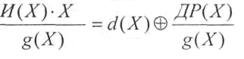<![endif]>

где d(Х) - целая часть результата деления.

Подставим полученную сумму на место первого слагаемого:

 

<![if !vml]>

<![endif]>
Суммирование последних двух слагаемых дает нулевой результат (напомним, что суммирование выполняется по модулю 2).

Значит

<![if !vml]>

<![endif]>
- целая часть деления. Остатка нет. Это означает, что описанный выше способ кодирования соответствует циклическому коду.

 

8.2 Некоторые свойства циклических кодов.

Все свойства циклических кодов определяются образующим полиномом.

1. Циклический код, образующий полином которого содержит более одного слагаемого, обнаруживает все одиночные ошибки.

Строго доказывать это не будем. Покажем это на примере простейшего образующего полинома g(X) =Х+1. Вектор однократной ошибки в i-м разряде описывается полиномом ВО(Х)=Хⁱ.

<![if !vml]>

<![endif]>
Найдем опознаватель

 

<![if !vml]><![endif]>

Таким образом, поскольку ВО имеет вес 1 (не равен нулю), ошибка обнаруживается.

2. Можно показать, что циклический код, образованный при помощи простейшего первообразного полинома g(Х)=Х+1, позволяет обнаруживать не только одиночные но и любые ошибки нечетной кратности. Доказательство базируется на том факте, что при использовании образующего полинома X+1получаемые в результате кодовые слова обязательно имеют четное число единичных разрядов.

Любое искажение с нечетным числом ошибок преобразует разрешенное кодовое слово с четным числом единиц в запрещенное слово с нечетным числом единиц. Такое кодовое слово, поскольку оно является запрещенным, сразу же будет обнаружено по наличию остатка от его деления на образующий полином.

 

Найдем теперь для случая образующего полинома Х+1упрощенный вариант процедуры кодирования.

Ранее была приведена следующая формула получения кодового слова (случай систематического кода):

<![if !vml]>

<![endif]>

Остатком от деления любого полинома на Х+1 может быть либо 0 (остатка нет) либо 1. Следовательно, r=1, то есть образующий полином Х+1 дает нам один дополнительный корректирующий разряд.

Учитывая вывод о том, что при использовании образующего полинома Х+1 получаемые в результате кодовые слова обязательно имеют четное число единичных разрядов, делаем вывод, что этот один разряд должен дополнять число единиц в информационной части кода до четного числа. В этом и заключается упрощенный способ кодирования при использовании разделимого циклического кода с образующим полиномом X+1.

 

8.3 Методы построения циклических кодов

Циклические коды можно, как и любые линейные коды, описывать с помощью матриц.

Вспомним, что

<![if !vml]>

<![endif]>

Вспомним также на примере порядок умножения полиномов:

<![if !vml]><![endif]>

 

Это соответствует описанному выше упрощенному способу умножения матриц:

 

<![if !vml]>

<![endif]>

Видно, что, если в качестве строк образующей матрицы взять наборы сдвинутых вправо коэффициентов образующего полинома, вычисление кодовых слов при помощи матриц полностью эквивалентно вычислению кодовых слов при помощи полиномов.

Согласно второму способу кодирования, позволяющего получить систематический код, кодовое слово находится по формуле:

 

<![if !vml]><![endif]>

 

Образующая матрица ||ОМ|| в этом случае должна состоять из 2 частей - единичной матрицы ||I|| и матрицы дополнительных разрядов ||МДР||, то есть:

 

||ОМ ||= || I, МДР || .

 

Результат кодирования при помощи матриц будет совпадать с результатом кодирования при помощи полиномов в том случае, если строки матрицы дополнительных разрядов образовать по следующей формуле:

 

i- аястрокаМДР= ост(( Xⁱ)/g_r(X)).

 

Далее по МДР легко построить ТПМ найти опознаватели и воспользоваться описанными выше для линейных кодов процедурами кодирования-декодирования.

 

8.4 Выбор образующего полинома.

Ясно, что полиномы кодовых слов КС(Х) должны делиться на образующий полином степени r без остатка. Циклические коды относятся к классу линейных. Это означает, что для этих кодов существует r линейно-независимых кодовых слов и с их помощью путем суммирования в разных комбинациях можно получить все остальные разрешенные кодовые слова данного кода. Для того, чтобы все они делились на образующий полином без остатка, достаточно чтобы без остатка на него делились только rлинейно независимых кодовых слов. Эти линейно-независимые кодовые слова можно получить путем r-кратного циклического сдвига вправо или влево любого из разрешенных кодовых слов.

<![if !vml]>

<![endif]>
Напомним, что сдвигу влево соответствует умножение кодового слова на X с последующим вычитанием, если в результате умножения получается полином порядка >n из результата полинома Xⁿ+1. В формульном виде вышесказанное может быть отображено следующим образом'

 

 

где В=1 если степень g(X)*Xⁱ>=n

и где В=0 если степень g(X)*Xⁱ<n

 

Частное g_i(X)/ g(X) не имеет остатка, если полином (Хⁿ+1) без остатка делится на образующий полином g(X) (очевидно, первое слагаемое делится на g(X) без остатка).

Таким образом, образующий полином g_r (X) циклического линейного кода должен делить полином Хⁿ+1 без остатка.

Это свойство обеспечивает отсутствие остатка при делении разрешенных кодовых слов на образующий полином. Таких слов 2^k. Всего же различных кодовых слов, которые могут быть получены на выходе канала связи 2ⁿ. Среди них 2^r-1 запрещенных, т.е. полученных в результате искажения разрешенных кодовых слов помехой. Ошибка обнаруживается, если остаток от их деления на образующий полином не равен нулю. Образующий полином имеет порядок r. Максимально возможное количество ненулевых остатков равно 2^r-1. Такое количество остатков могут дать только так называемые неприводимые полиномы, т.е. полиномы, которые не делятся без остатка ни на какие другие полиномы, кроме 1 и себя самого. Таблица неприводимых полиномов от 1 до 9 порядков приводятся в литературе.

Пример таблицы неприводимых полиномов.

Табл.8.1

Степень полинома	Полином	Двоичное слово
1	X+1	11
2	X2+X+1	111
3	X3+X+1	1011
3	X3+X2+1	1101
4	X4+X+1	10011
4	X4+X3+1	11001
4	X4+X3+X2+X+1	11111
9	X9+X+1	10000000001
	И еще 40 штук полиномов

 

8.5 Декодирование циклических кодов

 

Обнаружение и исправление ошибок происходит по остаткам от деления принятой комбинации F(X) на образующий полином G(X). Если принятая комбинация делится на образующий полином без остатка, то код принят безошибочно. Остаток от деления свидетельствует об ошибке, но не указывает, какой именно. Чтобы найти ошибочный разряд и исправить его в циклических кодах, принято осуществлять следующие процедуры:

 

1) принятая комбинация делится на образующий полином;

 

2) подсчитывается количество единиц в остатке (вес остатка).Если W<=S, где S-допустимое число исправляемых данным кодом ошибок, то принятая комбинация складывается по модулю 2 с полученным остатком. Сумма даст исправленную комбинацию. Если W>S, то

 

3) производим циклический сдвиг влево принятой комбинации, делим полученную в результате циклического сдвига комбинацию на образующий полином К(Х). Если в остатке W<=S, то складываем делимое с остатком. Затем производим циклический сдвиг вправо полученной комбинации. Полученная комбинация уже не содержит ошибок. Если после первого циклического сдвига и последующего деления остаток получается таким, что его вес W>S, то

 

4) повторяется процедура п.3) до тех пор, пока не будет W<=S. В этом случае

 

5) производиться циклический сдвиг вправо на столько разрядов, на сколько была сдвинута суммируемая с последним остатком комбинация относительно принятой комбинации. В результате получим исправленную комбинацию.

 

ПримерПоказать процесс исправления одиночной ошибки в принятой кодовой комбинации.

Пусть имеется кодовое слово циклического кода 1001110, в котором произошла ошибка в четвертом разряде и получен код 100011.

1. Делим принятую комбинацию на образующий полином g(X)=X³+X+1

<![if !vml]><![endif]>

2. Сравниваем вес полученного остатка W с возможным для данного кода числом исправляемых ошибок S. Вес остатка W=2. Число исправляемых ошибок S=1, т.е. W>S.

3. Производим циклический сдвиг принятой комбинации F(X) на один разряд влево с последующим делением полученной в результате циклического сдвига комбинации на g(Х):

 

4.Повторяем процедуру до тех пор, пока не будет W<S

 

<![if !vml]>

<![endif]>
5. Складываем по модулю 2 последнее делимое с последним остатком

<![if !vml]>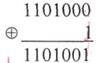<![endif]>

6. Производим циклический сдвиг комбинации, полученной в результате суммирования последнего делимого с последним остатком, вправо на 4 разряда (так как перед этим мы четырежды сдвигали принятую комбинацию влево)1110100, 0111010, 0011101, 1001110 как видим, последняя комбинация соответствует переданной, т. е. уже не содержит ошибки.

 

8.6 Контрольные вопросы.

1. Какой раздел математики используется при построении циклических кодов.

2. Основной медоед построения циклического кода.

3. Какова основная особенность работы с полиномиальным представлением двоичных кодов?

4. Назовите основные требования к образующим полиномам.

5. В чем неудобства исправления ошибок в циклических кодах?

Надеюсь, эта статья про двоичные циклические коды , была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое двоичные циклические коды и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория информации и кодирования

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.