Лекция
Привет, сегодня поговорим про метод эйлера, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое метод эйлера, метод усовершенствованного эйлера, метод модифицированного эйлера, численные методы интегрирования дифференциальных уравнений, шаг дискретизации, явная схема эйлера , настоятельно рекомендую прочитать все из категории Моделирование и Моделирование систем.
Пусть нам известна входная динамическая последовательность X (входной сигнал) и модель (способ преобразования входного сигнала в выходной сигнал). Рассматривается задача определения выходного сигнала y(t) (см. рис. 10.1).
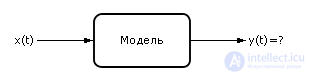
Рис. 10.1. Структурная модель динамической системы с одним входом и одним выходом
Модель динамической системы может быть представлена дифференциальным уравнением. Основное уравнение динамики:
y' = f(x(t), y(t), t).
Известны начальные условия в нулевой момент времени t0: y(t0), x(t0). Чтобы определить выходной сигнал, заметим, что по определению производной:
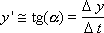
Нам известно положение системы в точке «1», требуется определить положение системы в точке «2». Точки отделены друг от друга расстоянием Δt (рис. 10.2). То есть расчет поведения системы производится по шагам. Из точки «1» мы скачком (дискретно) переходим в точку «2», расстояние между точками по оси t называется шагом расчета Δt.
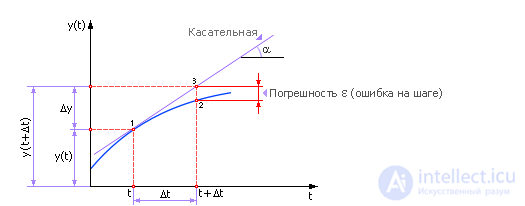
Рис. 10.2. Иллюстрация расчета будущего состояния системы методом Эйлера на одном шаге
Тогда:
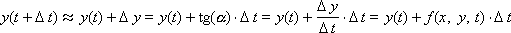
или
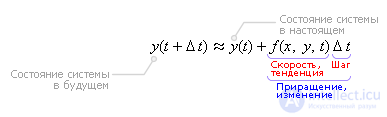
Последняя формула называется формулой Эйлера.
Очевидно, чтобы узнать состояние системы в будущем y(t + Δt), надо к настоящему состоянию системы y(t) прибавить изменение Δy, прошедшее за время Δt.
будущее = настоящее + изменение
будущее = настоящее + скорость · шаг
Рассмотрим еще раз это важное соотношение, выведя его из геометрических соображений (рис. 10.3).
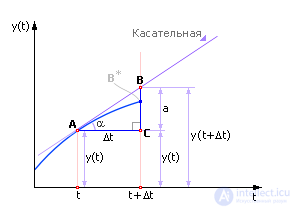

Рис. 10.3. Геометрическая иллюстрация метода Эйлера
Пусть A — точка, в которой состояние системы известно. Это «настоящее» состояние системы.
В точке A к траектории движения системы проведем касательную. Касательная — это производная функции f(x(t), y(t), t) по переменной t. Производную в точке всегда легко вычислить, достаточно подставить известные переменные (в момент «Настоящее» они известны) в формулуy' = f(x(t), y(t), t).
Заметим, что, по определению, производная связана с углом наклона касательной: y' = tg(α), значит, угол α легко вычислить (α = arctg(y' )) и провести касательную.
Проведем касательную до пересечения с линией t + Δt. Момент t + Δt соответствует «будущему» состоянию системы. Проведем линию параллельно оси t от точки A до пересечения с линией t + Δt. Линии образуют прямоугольный треугольник ABC, один катет которого равен Δt (известен). Известен также угол α. Тогда второй катет в прямоугольном треугольнике ABC равен: a = Δt · tg(α). Теперь легко вычислить ординату точки B. Она состоит из двух отрезков — y(t) и a. Ордината символизирует положение системы в точке y(t + Δt). То есть y(t + Δt) = y(t) + a или далее y(t + Δt) = y(t) + Δt · tg(α) или, подставляя дальше, имеем: y(t + Δt) = y(t) + Δt · y' и, наконец, y(t + Δt) = y(t) + Δt · f(x(t), y(t), t). Снова мы получили формулу Эйлера (из геометрических соображений).
Эта формула может дать точные результаты только при очень малых Δt (говорят при Δt –> 0). При Δt≠0 формула дает расхождение между истинным значением y и расчетным, равное ε, поэтому в ней должен стоять знак приближенного равенства, либо она должна быть записана так:
y(t + Δt) = y(t) + Δt · f(x(t), y(t), t) + ε.
И в самом деле. Взгляните еще раз на рис. 10.3. Будем мысленно сдвигать линию t + Δt влево (фактически, будем приближать значение Δt к нулю). Как нетрудно видеть, расстояние BB* = ε, — то есть ошибка! — будет сокращаться. В пределе (при Δt –> 0) значение ошибки ε будет равно нулю.
Итак, заменяя реальную кривую прямой (касательной) на отрезке Δt, мы вносим в решение ошибку, попадая в результате не в точку «2» (см. рис. 10.2), а рядом, в точку «3». Очевидно, что этот численный метод на каждом шаге имеет погрешность расчета ε.
Из рисунка видно, что чем меньше взять величину Δt, тем меньше будет ошибка расчета ε. То есть для расчета поведения системы на сколько-нибудь продолжительном отрезке времени (например, от t0 до tk), чтобы уменьшить ошибку на каждом шаге, шаги Δt делают по возможности малыми. Для достижения точки tk отрезок (tk – t0) делится на отрезки длиной Δt; таким образом, всего получитсяN = (tk – t0)/Δt шагов. В результате расчета придется формулу Эйлера применить для каждого шага, то есть N раз. Но следует иметь в виду, что ошибки εi на каждом i-ом шаге (в простейшем случае) складываются, а общая ошибка быстро накапливается (см. рис. 10.4). И в этом состоит существенный недостаток данного метода. Хотя с помощью этого метода можно получить (в численном виде) решение любого дифференциального уравнения (в том числе и неразрешимого аналитически). Уменьшая шаг, мы получаем более точные решения, но при этом не следует забывать, что увеличение числа шагов ведет к вычислительным затратам и снижению быстродействия. Кроме того, при большом числе итераций в расчет вносится другая существенная погрешность из-за ограниченной точности вычислительных машин и ошибок округления.
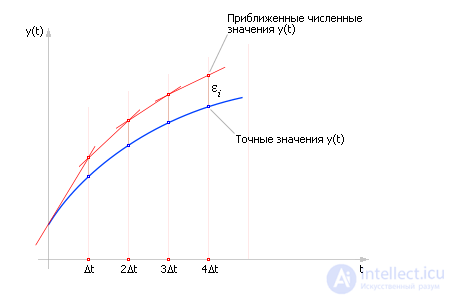
Рис. 10.4. Нарастание суммарной ошибки в методе Эйлера на ряде шагов
Задача 1. Дано дифференциальное уравнение y' = 2ty. Задано начальное положение системы:y(0) = 1. Требуется найти y(t), то есть поведение системы на интервале времени t от 0 до 1.
y' = 2ty.
Методом разделения переменных найдем:
y'/y = 2t
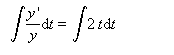
Будем интегрировать от 0 до ti, тогда согласно правилам интегрирования имеем:
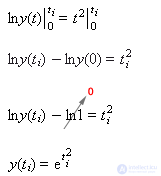
Полученное аналитическое решение характеризуется тем, что оно является абсолютно точным, но если уравнение окажется сколько-нибудь сложным, то решение не будет найдено вовсе. Аналитический путь решения не универсален.
Численный способ решения предполагает, что расчет будет вестись по формуле Эйлера на ряде последовательных шагов. На каждом шаге решение имеет свою ошибку (см. рис. 10.2), поскольку на каждом шаге кривая заменяется прямым отрезком.
При алгоритмической реализации расчет реализуется циклом, в котором изменяется t (счетчик t) и y:
t := t + Δt
y := y + 2 · t · y · Δt
Блок-схема при реализации метода на компьютере показана на рис. 10.5.
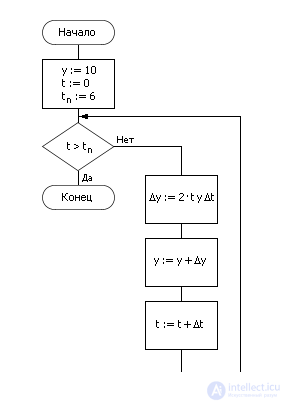
Рис. 10.5. Блок-схема реализации метода Эйлера
В реализации Стратум запись будет выглядеть так (наличие символа «~» при t):
t := t + Δt
y := y + 2 · ~t · y · Δt
Будем искать значение y рассмотренного ранее примера в численном виде на промежутке отT = 0 до T = 1. Об этом говорит сайт https://intellect.icu . Возьмем число шагов n = 10, тогда шаг приращения Δt составит: Δt = (1 – 0)/n = (1 – 0)/10 = 0.1.
Таблица 10.1. Численный расчет уравнения методом Эйлера и сравнение результата с точным решением на каждом шаге
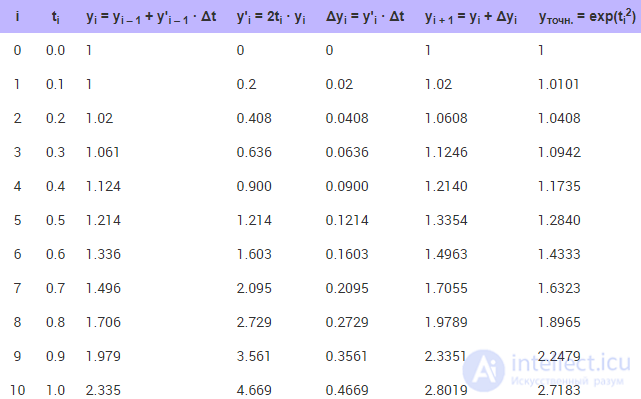
Обратите внимание на то, что рассчитанное численно значение (yi + 1) отличается от точного (yточн.), и погрешность (разница столбцов yi + 1 и yточн.) в процессе расчета нарастает подобно тому, как было показано на рис. 10.4.
Теперь подсчитаем относительную погрешность σ для расчетного значения y(1), полученного численно, в сравнении с теоретическим точным yтеор. по следующей формуле:
σ = (1 – yрасч./yтеор.) · 100%
и сравним σ при различных значениях Δt.
Если будем менять значение шага Δt, например, уменьшать шаг, то относительная погрешность расчета тоже будет уменьшаться. Вот что получится при вычислении значения y(1) с разными значениями шага (см. табл. 10.2).
Таблица 10.2. Зависимость погрешности расчета от размера шага Δt
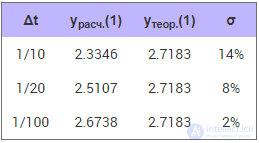
Как видим, с уменьшением шага приращения Δt уменьшается величина относительной погрешности, а значит, повышается точность расчета.
Обратите внимание, что изменение шага в 10 раз (с 1/10 до 1/100) ведет к изменению величины ошибки примерно тоже в 10 раз (с 14% до 2%). При изменении шага в 100 раз ошибка примерно уменьшится тоже в 100 раз. Иными словами размер шага и ошибка для метода Эйлера связаны линейно. Хотите уменьшить в 10 раз ошибку — уменьшайте в 10 раз шаг и увеличивайте соответственно в 10 раз количество вычислений. Этот факт в математике принято обозначать символом ε = O(Δt), а метод эйлера называют методом первого порядка точности.
Поскольку в методе Эйлера ошибка достаточно велика и от шага к шагу накапливается, а точность пропорциональна количеству вычислений, то метод Эйлера обычно применяют для грубых расчетов, для оценки поведения системы в принципе. Для точных количественных расчетов применяют более точные методы.
Примечания
Изложенное в пп. 1-4 поясним на примере.
Пример. Пусть
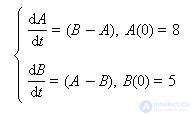
Качественно это уравнения описывают процесс теплообмена между двумя телами, температуры которых в некоторый момент времени обозначим как A и B. Вообще A и B — переменные, меняющиеся во времени t. Найти поведение системы означает, что надо найти, как будут меняться температуры A(t) и B(t).
Интуитивно ясно, что при начальной разнице температур A = 8 и B = 5 температуры тел постепенно со временем должны выровняться, так как более горячее тело будет отдавать энергию более холодному, и его температура будет уменьшаться, а более холодное тело будет принимать энергию от более горячего, и его температура будет увеличиваться. Процесс теплообмена закончится (то есть изменения прекратятся) тогда, когда температуры двух тел станут одинаковыми.
Проведем несколько расчетов поведения A(t) и B(t) с разной величиной шага Δt.
Будем брать различную величину шага Δt и находить соответствующие значения A и B во времени по следующим формулам Эйлера:
Aнов. = Aпред. + (Bпред. – Aпред.) · Δt,
Bнов. = Bпред. + (Aпред. – Bпред.) · Δt.
Расчет при Δt = 2 (табл. 10.3).
Таблица 10.3. Изменение температур тел при численном расчете с шагом 2
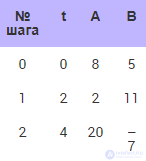
Наблюдается явление «разболтки» (см. рис. 10.6). Неустойчивое решение. Из физических соображений очевидно, что так вести себя два тела в процессе теплообмена не могут.
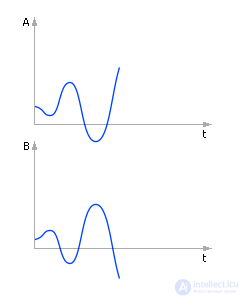
Рис. 10.6. Система ведет себя качественно неверно. Решение неустойчиво
Расчет при Δt = 1 (табл. 10.4).
Таблица 10.4. Изменение температур тел при численном расчете с шагом 1
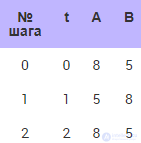
Наблюдается поведение решения системы на границе устойчивости (см. рис. 10.7).
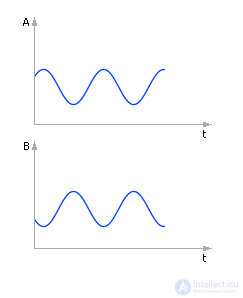
Рис. 10.7. Система ведет себя качественно неверно. Решение находится на грани устойчивости
Расчет при Δt = 0.5 (табл. 10.5).
Таблица 10.5. Изменение температур тел при численном расчете с шагом 0.5
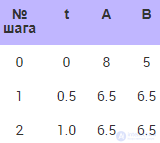
Решение устойчиво, соответствует правильной качественной картине (см. рис. 10.8). Температуры тел постепенно сближаются, становятся со временем одинаковыми. Но решение пока имеет большую погрешность.
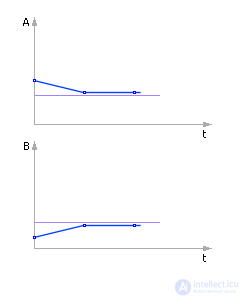
Рис. 10.8. Система ведет себя качественно правильно. Решение (поведение системы) имеет большую погрешность
Расчет при Δt = 0.1 (табл. 10.6).
Таблица 10.6. Изменение температур тел при численном расчете с шагом 0.1

Решение устойчиво. Решение более точно (см. рис. 10.9).
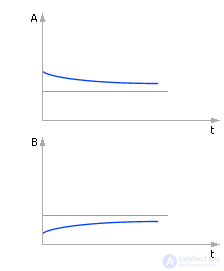
Рис. 10.9. Система ведет себя качественно верно. Количественно решение более точно
Роль изменения величины шага иллюстрирует рис. 10.10.
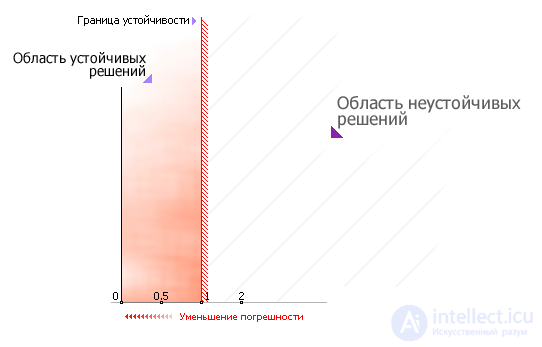
Рис. 10.10. Связь величины шага расчета с устойчивостью метода и его точностью (на примере)
С целью эффективного использования при интегрировании систем дифференциальных уравнений первого порядка, представленных в нормальной форме, средств вычислительной техники разработан целый ряд численных методов.
Пусть для системы дифференциальных уравнений первого порядка, записанных в нормальной форме 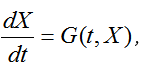 ,с начальными условиями Х(0) =X0 требуется решить задачу Коши во временном интервал 0 ≤ t ≤Т.Для применения численных методов необходимо перейти от непрерывной, или континуальной, формы записи системы дифференциальных уравнений к дискретной. С этой целью вся область интегрирования [0,T] разбивается на отрезки
,с начальными условиями Х(0) =X0 требуется решить задачу Коши во временном интервал 0 ≤ t ≤Т.Для применения численных методов необходимо перейти от непрерывной, или континуальной, формы записи системы дифференциальных уравнений к дискретной. С этой целью вся область интегрирования [0,T] разбивается на отрезки
0 = t01<…k<…M = T.
Тем самым непрерывной области изменения аргумента tставится в соответствие дискретная область изменения этого аргумента
(0 ≤ t ≤ Т) → (t0, t1, …, tM).
Величину 
 называют шагом дискретизации (шагом интегрирования), а саму дискретную область -сеточной областью. Будем далее полагать, чтоhk=h=const. Сеточную область при этом называют равномерной. Моментыtkносят название узлов сеточной области. Значения искомых функций в узлах сеточной области будем обозначатьX(tk) =Хk.Вk-ом узле сеточной области систему можно записать:
называют шагом дискретизации (шагом интегрирования), а саму дискретную область -сеточной областью. Будем далее полагать, чтоhk=h=const. Сеточную область при этом называют равномерной. Моментыtkносят название узлов сеточной области. Значения искомых функций в узлах сеточной области будем обозначатьX(tk) =Хk.Вk-ом узле сеточной области систему можно записать:
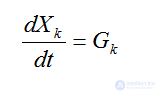 (2.29)
(2.29)
Предположим, что решение задачи Коши известно в узлах, предшествующих tk+1.При достаточной гладкости вектор-функцииG(t, X)(то есть существовании производных нужного порядка по всем переменным) используем разложениеX(t) в ряд Тейлора в окрестности точкиtk:
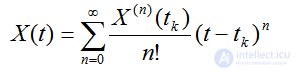 (2.30)
(2.30)
Полагая t=tk+1=tk+h, получим
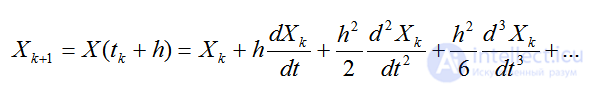 (2.31)
(2.31)
Из (4.31) находим:
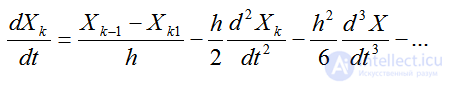 (2.32)
(2.32)
Подставляя это значение производной в (4.33),будем иметь
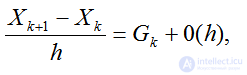 (2.33)
(2.33)
где 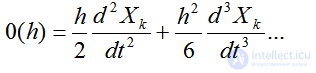
Выражение 0(h) называют обычно слагаемым порядка hи при h →0 представляет собой бесконечно малую величину. Отбрасывая в (4.36)слагаемое порядкаh, получаем
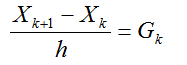 (2.34)
(2.34)
Система (4.37) является системой алгебраических, или, как обычно говорят, разностных уравнений и представляет собой дискретную форму записи системы дифференциальных уравнений 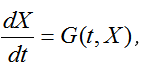 . Так как системы (4.36) и (4.37) отличаются на слагаемое0(h),то говорят, что система разностных уравнений аппроксимирует исходную систему дифференциальных уравнений с порядком0(h)или с первым порядком (первая степень h).
. Так как системы (4.36) и (4.37) отличаются на слагаемое0(h),то говорят, что система разностных уравнений аппроксимирует исходную систему дифференциальных уравнений с порядком0(h)или с первым порядком (первая степень h).
Следует отметать, что Xkв (4.36)и (4.37)различны: в (4.36) -это решение системы дифференциальных уравнений вk-ом узле, а в (4.37) -решение системы разностных уравнений.
В случае h →0 система (4.36)стремится принять вид (4.37).Естественно предположить, что при этом решения дифференциальных и разностных уравнений сближаются, и если hбудет достаточно мало, то и решения этих уравнений будут мало различаться.
Разрешая уравнение (4.37)относительноXk+1получим
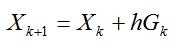 (2.35)
(2.35)
Эта реккурентная зависимость позволяет считать Xk+1по известномуXk.Система разностных уравнений (4.38)представляет собой пример простейшей численной схемы, которая носит название явной схемы Эйлера. Название явная следует из того, что схема (4.38)разрешима явным образом относительноXk+1.
Для математических моделей линейных электрических цепей с постоянными параметрами и постоянными задающими источниками явная схема эйлера принимает вид:
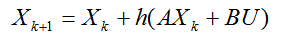 (2.36)
(2.36)
Явная схема Эйлера получена с помощью аппроксимации производной 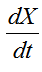 разностью вперед, то есть приращение вектор - функции X(t) в k-ом узле получалось с использованием ее значения в последующем узле k+1. Если аппроксимировать производную разностью назад, получим неявную схему Эйлера:
разностью вперед, то есть приращение вектор - функции X(t) в k-ом узле получалось с использованием ее значения в последующем узле k+1. Если аппроксимировать производную разностью назад, получим неявную схему Эйлера:
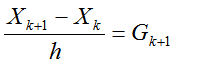 (2.37)
(2.37)
которая тоже имеет первый порядок аппроксимации. Название неявная следует изтого, что схема неразрешима явным образом относительноXk+1:
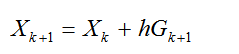 (2.38)
(2.38)
Для линейных электрических схем с постоянными параметрами и постоянными задающими источниками неявная схема Эйлера имеет вид:
Xk+1 = Xk + h(AXk+1 + BU). (2.39)
После преобразований будем иметь:
Xk+1 = (E – hA)-1(Xk + hBU). (2.40)
Явная и неявная схемы Эйлера обладают наименьшей точностью из всех численных схем интегрирования дифференциальных уравнений. Можно построить более точные численные схемы, имеющие более высокий порядок аппроксимации. Для этого при дискретизации системы 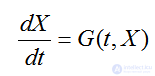 необходимо учесть большее количество членов разложения Xk+1 в ряд Тейлора(4.35).Так, использование двух членов этого разложения позволило получить явную схему Эйлера. Использование третьего члена позволит получить численную схему с порядком аппроксимации 0(h2),но для этого надо получить аппроксимацию производной
необходимо учесть большее количество членов разложения Xk+1 в ряд Тейлора(4.35).Так, использование двух членов этого разложения позволило получить явную схему Эйлера. Использование третьего члена позволит получить численную схему с порядком аппроксимации 0(h2),но для этого надо получить аппроксимацию производной 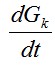 с порядком 0(h).При этом возможны различные варианты.
с порядком 0(h).При этом возможны различные варианты.
Представим производную в виде
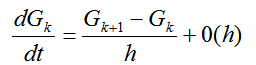 (2.41)
(2.41)
Учитывая, что 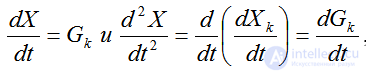 , представим (4.35)
, представим (4.35)
в виде
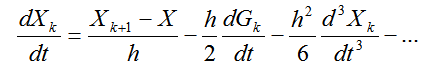 (2.42)
(2.42)
Подставляя (4.44) в (4.45), получим:
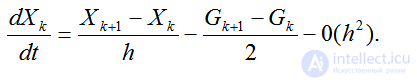 (2.43)
(2.43)
Тогда
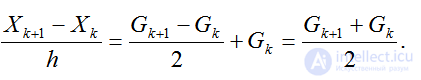 (2.44)
(2.44)
Данная численная схема носит название схемы трапеций.
Для моделей электрических цепей с постоянными параметрами и постоянными задающими источниками численная схема трапеций после преобразований имеет следующий вид:
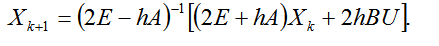 (2.45)
(2.45)
Как видно из (4.49), схема трапеций является неявной. С целью получения явных зависимостей ее можно модифицировать. Для этого надо найти аппроксимацию 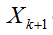 с порядком
с порядком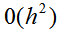 и подставить ее в правую часть (4.49). При этом порядок аппроксимации численной схемы останется
и подставить ее в правую часть (4.49). При этом порядок аппроксимации численной схемы останется 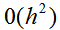 .Такому условию соответствует пара формул:
.Такому условию соответствует пара формул:
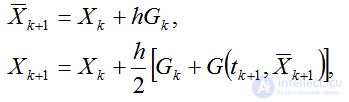 (2.46)
(2.46)
где для аппроксимации Xk+1используется численная схема Эйлера (первая формула). полученную численную схему можно переписать в виде:
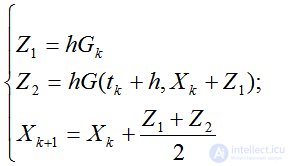 (2.47)
(2.47)
Численная схема (4.51) называется модифицированной схемой трапеций.
Представим теперь производную в виде
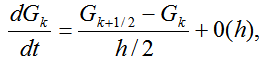 (2.48)
(2.48)
где 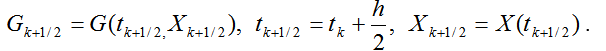 .
.
Для аппроксимации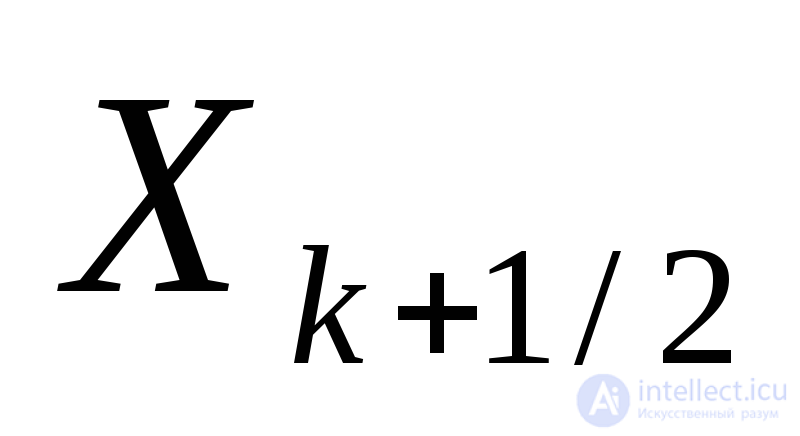 порядком 0(h2)снова выберем явную схему Эйлера. Действуя аналогично предыдущему, находим:
порядком 0(h2)снова выберем явную схему Эйлера. Действуя аналогично предыдущему, находим:
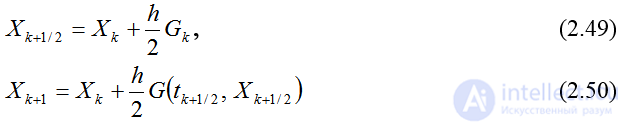
или
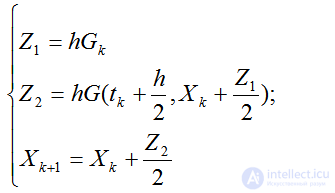 (2.51)
(2.51)
Численные схемы (4.51) и (4.53) относятся к семейству схем Рунге-Кутта. В обобщенном виде численные схемы Рунге-Кутта представляются как:
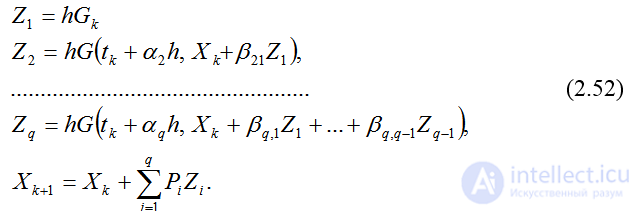
Здесь q-порядок аппроксимации, а параметры
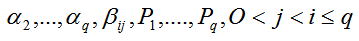 подбираются таким образом, чтобы
подбираются таким образом, чтобы
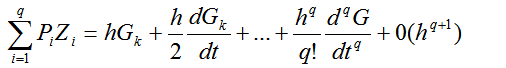 (2.53)
(2.53)
При q=1легко находитсяР1= 1,и схема Рунге-Кутта совпадает с явной схемой Эйлера. Приq>1система уравнений относительно параметров имеет неединственное решение, что означает неединственность схем Рунге-Кутта с одним и тем же порядком аппроксимации. С ростомqрезко возрастает трудоемкость проведения аналитических выкладок для определения параметров схемы. Численные схемы (4.51) и (4.53) соответствуют случаюq=2.
Одна из наиболее употребительных численных схем Рунге-Кутта с порядком аппроксимации 0(h4)(схема Рунге-Кутта четвертого порядка )имеет вид:
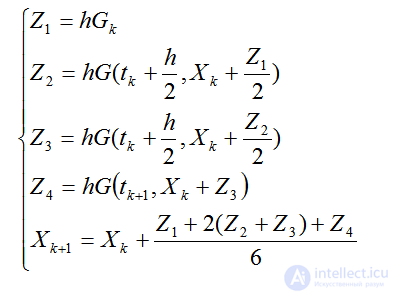 (2.54)
(2.54)




Эйлер
Усовершенствованный (модифицированный)Эйлер (усовершенственный эйлер)


Надеюсь, эта статья об увлекательном мире метод эйлера, была вам интересна и не так сложна для восприятия как могло показаться. Желаю вам бесконечной удачи в ваших начинаниях, будьте свободными от ограничений восприятия и позвольте себе делать больше активности в изученном направлени . Надеюсь, что теперь ты понял что такое метод эйлера, метод усовершенствованного эйлера, метод модифицированного эйлера, численные методы интегрирования дифференциальных уравнений, шаг дискретизации, явная схема эйлера и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Моделирование и Моделирование систем
Комментарии
Оставить комментарий
Моделирование и Моделирование систем
Термины: Моделирование и Моделирование систем