Лекция
Привет, Вы узнаете о том , что такое электрическое поле в вакууме, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое электрическое поле в вакууме , настоятельно рекомендую прочитать все из категории Переменный электрический ток. Электромагнитное поле.
История утверждает, что греческий философ Фалес (рис. 1.1) более двадцати пяти столетий назад наблюдал действие электрических сил: он обнаружил, что янтарь, будучи натертым шерстяной фланелью, способен притягивать легкие предметы. Янтарь — на греческом «электрон» — дал нам термин «электричество».

Рис. 1.1. Фалес (625–547 до нашей эры) — древнегреческий философ и ученый
Древние греки были знакомы и с особыми свойствами железной руды (магнетит или магнитный железняк), являющейся природным магнитом. Слово «магнит» происходит от греческого «камень из Магнесии» — по имени города в Малой Азии, вблизи которого имелось месторождение этой руды.
Систематическое изучение электричества и магнетизма началось в эпоху Возрождения, однако только к концу прошлого столетия физики достигли ясного понимания основ классической теории этих явлений.
Все тела в природе образованы из атомов или молекул, которые, в свою очередь, состоят из ядер и электронов, обладающих электрическим зарядом.
Электрический заряд является феноменологической характеристикой свойств элементарных частиц и их взаимодействий.
Между заряженными элементарными частицами существуют особые силы взаимодействия, называемые электрическими силами. Экспериментально установлено, что эти силы могут быть как силами притяжения, так и силами отталкивания, поэтому для описания электрического взаимодействия вводятся два типа электрических зарядов, условно называемых отрицательными и положительными: одноименные заряды отталкиваются, а разноименные — притягиваются (рис. 1.2).

Рис. 1.2. Два отрицательных заряда отталкиваются, отрицательный и положительный заряды притягиваются, два положительных заряда отталкиваются
Заряд электронов считается отрицательным, заряд протонов — положительным. Входящие в состав ядер нейтроны электрического заряда не имеют. Силы электрического взаимодействия связывают ядро и электроны в единую устойчивую систему — атом.
Наименьший по величине электрический заряд, экспериментально обнаруженный в природе, — заряд электрона. Заряд протона точно равен ему по величине и противоположен по знаку:

|
Электрический заряд протона |
Отметим, что приведенное выше значение элементарного заряда обычно используется для приближенных расчетов и при решении учебных школьных и ВУЗовских задач. На самом деле физики-экспериментаторы определили его с гораздо большей точностью. В настоящее время в таблицах (Journal of Physics G. Nuclear and Particle Physics. Vol. 37, № 7А, July 2010, Article 075021) приводится следующее значение элементарного заряда

Ввиду точного равенства величин зарядов протона и электрона в каждом атоме суммарный положительный и отрицательный заряды одинаковы по величине, и поэтому обычно тела оказываются электронейтральными. Однако, прилагая некоторые усилия, можно оторвать электроны от одних тел, которые становятся при этом положительно заряженными, и передать их другим телам, которые заряжаются отрицательно. Такие тела являются макроскопически заряженными. Электрический заряд любого тела кратен элементарному заряду e, то есть изменяется дискретно:
|
|
(1.1) |
где N — целое число. О дискретности возможных значений электрического заряда принято говорить как о квантовании электрического заряда.
Многочисленные эксперименты доказали, что имеет место закон сохранения электрического заряда:
|
В любой электроизолированной системе заряженных тел суммарный электрический заряд сохраняется:
|
Электроизолированной принято называть такую физическую систему, граничную поверхность которой заряженные частицы пересекать не могут. Поэтому во многих случаях, в частности, при выводе уравнений, являющихся интегральной или дифференциальной формой записи закона сохранения заряда весьма полезна такая его формулировка:
|
Единственным способом изменения заряда любой физической системы является внесение в систему заряженных частиц через ее граничную поверхность. |
Очевидно, что «вносить» в систему или «выносить» из системы заряженные частицы — в алгебраическом смысле одно и то же. Отметим также, что подобный подход оказывается продуктивным и при записи других законов сохранения: энергии, импульса, момента импульса и т. п.
На микроскопическом уровне закон сохранения заряда следует из анализа реакций между элементарными частицами и, конечно, ядерных реакций. Возьмем, например, альфа-распад изотопа урана (рис. 1.3):


Рис. 1.3. Альфа-распад изотопа урана-238
Атомный номер Z ядра урана равен 92, что означает, что в ядре находится 92 протона, то есть его заряд равен qU = 92e. У тория Z = 90, то есть заряд его ядра qTh=90e, а для гелия Z = 2 и qHe = 2e. Выполнение равенства
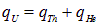
и означает сохранение электрического заряда в данной реакции. Никогда не наблюдались реакции с участием ядер или элементарных частиц, в которых бы нарушался закон сохранения электрического заряда. Это не означает, что частицы с электрическим зарядом не могут исчезать или рождаться, но при этом также должны исчезнуть или родиться частицы с таким же, но противоположным по знаку зарядом. Главное, чтобы суммарный заряд до и после реакции оставался неизменным. Приведем в качестве примера так называемую реакцию аннигиляции: электрон e– с зарядом –e сталкивается со своей античастицей — позитроном e+, заряд которого положителен и равен +e. В результате рождаются два фотона g (рис. 1.4).

Рис. 1.4. Реакция аннигиляции электрона и позитрона
Легко убедиться, что реакция

удовлетворяет закону сохранения электрического заряда: полный заряд до и после реакции равен нулю. В то же время никогда не наблюдалась такая, например, реакция
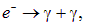
в которой заряд не сохраняется.
Электрон — самая легкая из заряженных частиц, и благодаря закону сохранения заряда (и закону сохранения энергии) ему просто не на что распадаться. Поэтому электрон стабилен, и это есть необходимая предпосылка стабильности атомов, молекул, вещества и нас с вами.
Пусть имеются два заряженных макроскопических тела, размеры которых пренебрежимо малы по сравнению с расстоянием между ними. В этом случае каждое тело можно считать материальной точкой или «точечным зарядом».
Французский физик Ш. Кулон (1736–1806) экспериментально установил закон, носящий его имя (закон Кулона) (рис. 1.5):

Рис. 1.5. Ш. Куло́н (1736–1806) — французский инженер и физик
|
В вакууме сила взаимодействия двух неподвижных точечных зарядов пропорциональна величине каждого из зарядов, обратно пропорциональна квадрату расстояния между ними и направлена по прямой, соединяющей эти заряды:
|
На рис. 1.6 показаны электрические силы отталкивания, возникающие между двумя одноименными точечными зарядами.

Рис. 1.6. Электрические силы отталкивания между двумя одноименными точечными зарядами
Напомним, что  , где
, где  и
и  — радиус-векторы первого и второго зарядов, поэтому силу, действующую на второй заряд в результате его электростатического — «кулоновского» взаимодействия с первым зарядом можно переписать в следующем «развернутом» виде
— радиус-векторы первого и второго зарядов, поэтому силу, действующую на второй заряд в результате его электростатического — «кулоновского» взаимодействия с первым зарядом можно переписать в следующем «развернутом» виде
|
|
(1.3) |
Отметим следующее, удобное при решении задач, правило: если первым индексом у силы ставить номер того заряда, на который действует эта сила, а вторым – номер того заряда, который создает эту силу, то соблюдение того же порядка индексов в правой части формулы автоматически обеспечивает правильное направление силы — соответствующее знаку произведения зарядов:  — отталкивание и
— отталкивание и  — притяжение, при этом коэффициент
— притяжение, при этом коэффициент  всегда.
всегда.
Для измерения сил, действующих между точечными зарядами, был использован созданный Кулоном прибор, называемый крутильными весами (рис. 1.7, 1.8).
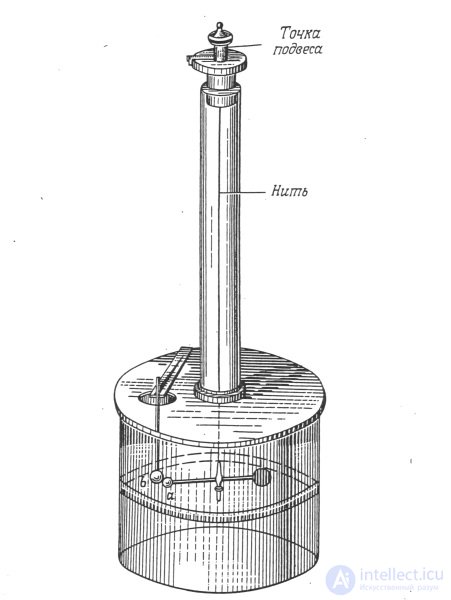
Рис. 1.7. Крутильные весы Ш. Кулона (рисунок из работы 1785 г.). Измерялась сила, действующая между заряженными шарами a и b

Рис. 1.8. Крутильные весы Ш. Кулона (точка подвеса)
На тонкой упругой нити подвешено легкое коромысло, на одном конце которого укреплен металлический шарик, а на другом — противовес. Рядом с первым шариком можно расположить другой такой же неподвижный шарик. Стеклянный цилиндр защищает чувствительные части прибора от движения воздуха.
Чтобы установить зависимость силы электростатического взаимодействия от расстояния между зарядами, шарикам сообщают произвольные заряды, прикасаясь к ним третьим заряженным шариком, укрепленным на ручке из диэлектрика. По углу закручивания упругой нити можно измерить силу отталкивания одноименно заряженных шариков, а по шкале прибора — расстояние между ними.
Надо сказать, что Кулон не был первым ученым, установившим закон взаимодействия зарядов, носящий теперь его имя: за 30 лет до него к такому же выводу пришел Б. Франклин. Более того, точность измерений Кулона уступала точности ранее проведенных экспериментов (Г. Кавендиш).
Чтобы ввести количественную меру для определения точности измерений, предположим, что на самом деле сила взаимодействия зарядов обратна не квадрату расстояния между ними, а какой-то другой степени:
 .
.
Никто из ученых не возьмется утверждать, что d = 0 точно. Правильное заключение должно звучать так: эксперименты показали, что d не превышает...
Результаты некоторых из этих экспериментов приведены в таблице 1.
Таблица 1.
Результаты прямых экспериментов по проверке закона Кулона
|
Эксперимент |
Год |
d |
|
Робинсон |
1769 |
<0,06 |
|
Кавендиш |
1773 |
<0,02 |
|
Кулон |
1785 |
0,02 |
|
Максвелл |
1873 |
<5·10–5 |
|
Плимтон, Лоутон |
1936 |
<2·10–9 |
|
Барлетт и др. |
1970 |
<1,3·10–13 |
|
Уильямс и др. |
1971 |
<3,0·10–16 |
Сам Шарль Кулон проверил закон обратных квадратов с точностью до нескольких процентов. В таблице приведены результаты прямых лабораторных экспериментов. Косвенные данные, основанные на наблюдениях магнитных полей в космическом пространстве, приводят к еще более сильным ограничениям на величину d. Таким образом, закон Кулона можно считать надежно установленным фактом.
В СИ единица силы тока (ампер) является основной, следовательно, единица заряда q оказывается производной. Как мы увидим в дальнейшем, сила тока I определяется как отношение заряда  , протекающего через поперечное сечение проводника за время
, протекающего через поперечное сечение проводника за время  , к этому времени:
, к этому времени:

Отсюда видно, что сила постоянного тока численно равна заряду, протекающему через поперечное сечение проводника за единицу времени, соответственно этому:
|
В СИ единицей измерения электрического заряда является кулон (Кл) — электрический заряд, протекающий за 1 секунду через поперечное сечение проводника при постоянной силе тока в 1 A:
|
Коэффициент пропорциональности в законе Кулона записывается в виде:
|
|
(1.4) |
При такой форме записи из эксперимента следует значение величины 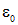 , которую принято называть электрической постоянной. Приближенное численное значение электрической постоянной следующее:
, которую принято называть электрической постоянной. Приближенное численное значение электрической постоянной следующее:

Поскольку 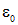 чаще всего входит в уравнения в виде комбинации
чаще всего входит в уравнения в виде комбинации

приведем численное значение самого коэффициента 

Как и в случае элементарного заряда, численное значение электрической постоянной определено экспериментально с высокой точностью:

Кулон — слишком большая единица для использования на практике. Например, два заряда в 1 Кл каждый, расположенные в вакууме на расстоянии 100 м друг от друга, отталкиваются с силой

Для сравнения: с такой силой давит на землю тело массой

Это примерно масса грузового железнодорожного вагона, например, с углем.
Принцип суперпозиции представляет собой утверждение, согласно которому результирующий эффект сложного процесса воздействия представляет собой сумму эффектов, вызываемых каждым воздействием в отдельности, при условии, что последние взаимно не влияют друг на друга (Физический энциклопедический словарь, Москва, «Советская энциклопедия», 1983, стр. 731). Экспериментально установлено, что принцип суперпозиции справедлив для рассматриваемого здесь электромагнитного взаимодействия.
В случае взаимодействия заряженных тел принцип суперпозиции проявляет себя следующим образом: сила, с которой данная система зарядов действует на некоторый точечный заряд, равна векторной сумме сил, с которыми действует на него каждый из зарядов системы.
Поясним это на простом примере. Пусть имеются два заряженных тела, действующие на третье с силами 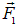 и
и  соответственно. Тогда система из этих двух тел — первого и второго — действует на третье тело с силой
соответственно. Тогда система из этих двух тел — первого и второго — действует на третье тело с силой

Это правило справедливо для любых заряженных тел, не только для точечных зарядов. Силы взаимодействия двух произвольных систем точечных зарядов вычисляются в Дополнении 1 в конце этой главы.
Отсюда следует, что электрическое поле системы зарядов определяется векторной суммой напряженностей полей, создаваемых отдельными зарядами системы, т. е.

Сложение напряженностей электрических полей по правилу сложения векторов выражает так называемый принцип суперпозиции (независимого наложения) электрических полей. Физический смысл этого свойства заключается в том, что электростатическое поле создается только покоящимися зарядами. Значит, поля различных зарядов «не мешают» друг другу, и поэтому суммарное поле системы зарядов можно подсчитать как векторную сумму полей от каждого из них в отдельности.
Так как элементарный заряд весьма мал, а макроскопические тела содержат очень большое количество элементарных зарядов, то распределение зарядов по таким телам в большинстве случаев можно считать непрерывным. Для того чтобы описать как именно распределен (однородно, неоднородно, где зарядов больше, где их меньше и т. п.) заряд по телу введем плотности заряда следующих трех видов:
· объемная плотность заряда 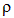 :
:
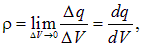
где dV — физически бесконечно малый элемент объема;
· поверхностная плотность заряда  :
:

где dS — физически бесконечно малый элемент поверхности;
· линейная плотность заряда  :
:

где  — физически бесконечно малый элемент длины линии.
— физически бесконечно малый элемент длины линии.
Здесь всюду 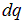 — заряд рассматриваемого физически бесконечно малого элемента (объема, участка поверхности, отрезка линии). Под физически бесконечно малым участком тела здесь и ниже понимается такой его участок, который, с одной стороны, настолько мал, что в условиях данной задачи, его можно считать материальной точкой, а, с другой стороны, он настолько велик, что дискретностью заряда (см. соотношение ) этого участка можно пренебречь.
— заряд рассматриваемого физически бесконечно малого элемента (объема, участка поверхности, отрезка линии). Под физически бесконечно малым участком тела здесь и ниже понимается такой его участок, который, с одной стороны, настолько мал, что в условиях данной задачи, его можно считать материальной точкой, а, с другой стороны, он настолько велик, что дискретностью заряда (см. соотношение ) этого участка можно пренебречь.
Общие выражения для сил взаимодействия систем непрерывно распределенных зарядов приведены в Дополнении 2 в конце главы.
Пример 1. Электрический заряд 50 нКл равномерно распределен по тонкому стержню длиной 15 см. На продолжении оси стержня на расстоянии 10 см от ближайшего его конца находится точечный заряд 100 нКл (рис. 1.9). Определить силу взаимодействия заряженного стержня и точечного заряда.
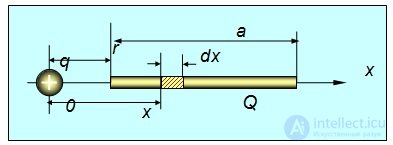
Рис. 1.9. Взаимодействие заряженного стержня с точечным зарядом
Решение. В этой задаче силу F нельзя определить, написав закон Кулона в форме или (1.3). В самом деле, чему равно расстояние между стержнем и зарядом: r, r + a/2, r + a? Поскольку по условиям задачи мы не имеем права считать, что a << r, применение закона Кулона в его исходной формулировке, справедливой только для точечных зарядов невозможно, необходимо использовать стандартный для таких ситуаций прием, который состоит в следующем.
|
Если известна сила взаимодействия точечных тел (например, закон Кулона) и необходимо найти силу взаимодействия протяженных тел (например, вычислить силу взаимодействия двух заряженных тел конечных размеров), то необходимо разбить эти тела на физически бесконечно малые участки, написать для каждой пары таких «точечных» участков известное для них соотношение и, воспользовавшись принципом суперпозиции, просуммировать (проинтегрировать) по всем парам этих участком. |
Всегда полезно, если не сказать — необходимо, прежде чем приступать к конкретизации и выполнению расчета, проанализировать симметрию задачи. С практической точки зрения такой анализ полезен тем, что, как правило, при достаточно высокой симметрии задачи, резко сокращает число величин, которые надо вычислять, поскольку выясняется, что многие из них равны нулю.
Разобьем стержень на бесконечно малые отрезки длиной  , расстояние от левого конца такого отрезка до точечного заряда равно
, расстояние от левого конца такого отрезка до точечного заряда равно  .
.
Равномерность распределения заряда 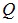 по стержню означает, что линейная плотность заряда
по стержню означает, что линейная плотность заряда  постоянна и равна
постоянна и равна
 ,
,
Следовательно, заряд  отрезка
отрезка  равен
равен  , откуда, в соответствии с законом Кулона, сила, действующая на точечный заряд q в результате его взаимодействия с точечным зарядом
, откуда, в соответствии с законом Кулона, сила, действующая на точечный заряд q в результате его взаимодействия с точечным зарядом  , равна
, равна

В результате взаимодействия точечного заряда q со всем стержнем, на него будет действовать сила
|
|
(1.5) |
Подставляя сюда численные значения, для модуля силы получаем:
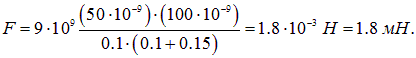
Из (1.5) видно, что при  , когда стержень можно считать материальной точкой, выражение для силы взаимодействия заряда и стержня, как и должно быть, принимает обычную форму закона Кулона для силы взаимодействия двух точечных зарядов:
, когда стержень можно считать материальной точкой, выражение для силы взаимодействия заряда и стержня, как и должно быть, принимает обычную форму закона Кулона для силы взаимодействия двух точечных зарядов:

Пример 2. Кольцо радиусом  несет равномерно распределенный заряд
несет равномерно распределенный заряд 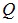 . Какова сила взаимодействия кольца с точечным зарядом q, расположенным на оси кольца на расстоянии
. Какова сила взаимодействия кольца с точечным зарядом q, расположенным на оси кольца на расстоянии 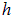 от его центра (рис. 1.10).
от его центра (рис. 1.10).
Решение. По условию, заряд 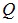 равномерно распределен на кольце радиусом
равномерно распределен на кольце радиусом  . Разделив
. Разделив 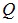 на длину окружности, получим линейную плотность заряда на кольце
на длину окружности, получим линейную плотность заряда на кольце  Выделим на кольце элемент длиной
Выделим на кольце элемент длиной  . Его заряд равен
. Его заряд равен  .
.

Рис. 1.10. Взаимодействия кольца с точечным зарядом
В точке q этот элемент создает электрическое поле

Нас интересует лишь продольная компонента поля, ибо при суммировании вклада от всех элементов кольца только она отлична от нуля:
|
|
продолжение следует...
Часть 1 1. Электрическое поле в вакууме
Часть 2 1.3. Электрическое поле. Напряженность и потенциал поля - 1. Электрическое
Часть 3 - 1. Электрическое поле в вакууме
Часть 4 1.4. Поток вектора. Теорема Остроградского-Гаусса для вектора - 1. Электрическое
Часть 5 1.5. Применение теоремы Гаусса для расчетов напряженности электрического поля -
Часть 6 Дополнения - 1. Электрическое поле в вакууме
Часть 7 Дополнение 2. Сила взаимодействия систем непрерывно распределенных зарядов - 1.
Комментарии
Оставить комментарий
Базовая физика
Термины: Базовая физика