Лекция
Это продолжение увлекательной статьи про электрическое поле в вакууме.
...
поверхность равен полному заряду внутри этой поверхности деленному на 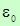
|
|
(1.34) |
Подчеркнем еще раз тривиальное, но важное обстоятельство: если внутри поверхности нет зарядов, то поток вектора 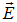 через эту поверхность равен нулю (рис. 1.40). Источниками электростатического поля являются электрические заряды и суммарная мощность источников электростатического поля внутри поверхности равна
через эту поверхность равен нулю (рис. 1.40). Источниками электростатического поля являются электрические заряды и суммарная мощность источников электростатического поля внутри поверхности равна 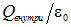 . Присутствие в последней формуле электрической постоянной
. Присутствие в последней формуле электрической постоянной 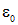 есть результат выбора системы единиц (СИ) и физического смысла не имеет.
есть результат выбора системы единиц (СИ) и физического смысла не имеет.
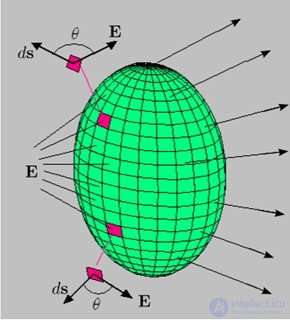
Рис. 1.40. Если внутри поверхности нет зарядов, то поток вектора 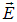 через эту поверхность равен нулю
через эту поверхность равен нулю
При непрерывном распределении заряда по объему теорему Гаусса естественно записать в следующем виде
|
|
(1.35) |
В правой части этого соотношения интеграл берется по объему 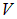 ограниченному поверхностью
ограниченному поверхностью 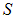 , поток
, поток 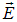 через которую вычисляется в левой его части. При непрерывном распределении заряда по некоторой поверхности справа будет стоять интеграл вида
через которую вычисляется в левой его части. При непрерывном распределении заряда по некоторой поверхности справа будет стоять интеграл вида 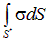 только по той части
только по той части 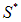 несущей заряд поверхности, которая оказалась внутри поверхности
несущей заряд поверхности, которая оказалась внутри поверхности 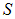 , стоящей слева. При непрерывном распределении заряда вдоль некоторой линии
, стоящей слева. При непрерывном распределении заряда вдоль некоторой линии 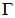 справа будет стоять интеграл вида
справа будет стоять интеграл вида  также только по той части
также только по той части 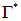 несущей заряд линии, которая оказалась внутри поверхности
несущей заряд линии, которая оказалась внутри поверхности 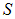 . Короче, необходимо любым приемлемым способом вычислить заряд внутри той замкнутой поверхности, по которой вычисляется поток вектора напряженности электрического поля.
. Короче, необходимо любым приемлемым способом вычислить заряд внутри той замкнутой поверхности, по которой вычисляется поток вектора напряженности электрического поля.
Примеры расчета полей, в которых главным инструментом является теорема Гаусса, даны в следующем разделе 1.5.
Теорема Гаусса для вектора 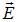
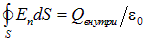
может быть успешно использована как эффективный инструмент расчета напряженности и потенциала электрического поля некоторого распределения заряда, когда стоящий слева интеграл может быть превращен в произведение площади поверхности, по которой производится интегрирование, на величину нормальной к поверхности составляющей 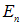 вектора
вектора 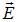 , то есть когда
, то есть когда
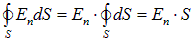 .
.
Вполне очевидно, что для расчета вектора 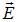 этого будет достаточно, во-первых, когда вектор
этого будет достаточно, во-первых, когда вектор 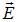 перпендикулярен поверхности. Следовательно, поверхность интегрирования должна быть эквипотенциальной поверхностью рассчитываемого поля. Ее форму надо знать заранее. Наконец, во-вторых, во всех точках этой — эквипотенциальной — поверхности нормальная к ней составляющая
перпендикулярен поверхности. Следовательно, поверхность интегрирования должна быть эквипотенциальной поверхностью рассчитываемого поля. Ее форму надо знать заранее. Наконец, во-вторых, во всех точках этой — эквипотенциальной — поверхности нормальная к ней составляющая 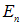 должна иметь одну и ту же величину, в противном случае, ее нельзя будет вынести из-под знака интеграла и будет возможно найти лишь среднее на эквипотенциальной поверхности значение
должна иметь одну и ту же величину, в противном случае, ее нельзя будет вынести из-под знака интеграла и будет возможно найти лишь среднее на эквипотенциальной поверхности значение 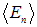 . Подчеркнем, что из факта эквипотенциальности поверхности, а именно, из того, что
. Подчеркнем, что из факта эквипотенциальности поверхности, а именно, из того, что
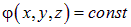
вовсе не вытекает, что и
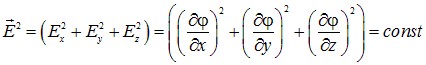
в точках этой поверхности. Забегая вперед, укажем, что, например, поверхность заряженного проводника при условии равновесного распределения заряда на нем всегда эквипотенциальна, но, если это не шар, а тело сложной формы, то в окрестности выступов (острий) напряженность поля может быть на порядки больше, чем в окрестности впадин на поверхности. Требование постоянства  — отдельное требование.
— отдельное требование.
Из сказанного выше вытекает, что теорема Гаусса в состоянии быстро и просто привести к результату (вектору 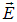 ) лишь в том случае, когда создающее поле распределение заряда обладает высокой степенью симметрии, соответственно, заранее известна форма эквипотенциальных поверхностей поля и есть уверенность в том, что
) лишь в том случае, когда создающее поле распределение заряда обладает высокой степенью симметрии, соответственно, заранее известна форма эквипотенциальных поверхностей поля и есть уверенность в том, что 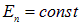 на этих поверхностях. Если все это имеет место, то решение выглядит следующим простым образом:
на этих поверхностях. Если все это имеет место, то решение выглядит следующим простым образом:
|
|
(1.36) |
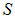 согласно симметрии распределения заряда и вычислить заряд внутри
согласно симметрии распределения заряда и вычислить заряд внутри 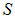 .
.
Сферическая симметрия
При сферически симметричном распределении заряда поле, создаваемое им, также сферически симметрично. Векторные (и скалярные) поля с такой симметрией принято также называть центральными полями. Центрально симметричное поле в общем случае можно записать в виде
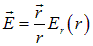 .
.
Здесь  — радиус-вектор, начинающийся в центре симметрии поля r — его модуль,
— радиус-вектор, начинающийся в центре симметрии поля r — его модуль, 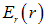 — радиальная составляющая напряженности поля, зависящая только от расстояния
— радиальная составляющая напряженности поля, зависящая только от расстояния 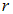 до его центра симметрии. Потенциал такого поля зависит только от
до его центра симметрии. Потенциал такого поля зависит только от 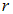 и
и
|
|
(1.37) |
И, кроме того, как следует из , при произвольной нормировке потенциал поля имеет вид
|
|
(1.38) |
Таким образом, условия применимости выполнены и мы можем воспользоваться этим соотношением.
Возьмем в качестве 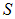 эквипотенциальную сферическую поверхность некоторого текущего радиуса r, ее площадь
эквипотенциальную сферическую поверхность некоторого текущего радиуса r, ее площадь 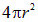 . Виду предполагаемой непрерывности распределения заряда, для
. Виду предполагаемой непрерывности распределения заряда, для 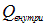 используем выражение:
используем выражение:
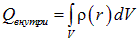 .
.
где 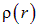 — объемная плотность заряда. Опять-таки, учитывая сферическую симметрию распределения заряда —
— объемная плотность заряда. Опять-таки, учитывая сферическую симметрию распределения заряда — 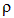 зависит только от
зависит только от 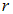 , в качестве элемента объема
, в качестве элемента объема 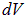 естественно взять бесконечно тонкий сферический слой с внутренним радиусом
естественно взять бесконечно тонкий сферический слой с внутренним радиусом 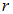 и внешним радиусом
и внешним радиусом 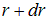 . Объем такого слоя
. Объем такого слоя 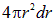 , в результате получаем
, в результате получаем
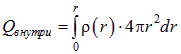 .
.
Окончательно, для любого сферически симметричного распределения заряда, когда 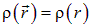 , получаем
, получаем
|
|
(1.39) |
Продолжение вычислений требует конкретизации вида зависимости плотности заряда 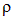 от модуля радиус-вектора
от модуля радиус-вектора 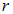 .
.
Поле однородно по объему заряженного шара
Равномерное по объему шара радиуса 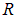 распределение заряда
распределение заряда 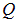 (рис. 1.41) означает, что его плотность заряда
(рис. 1.41) означает, что его плотность заряда 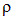 имеет вид
имеет вид
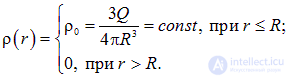
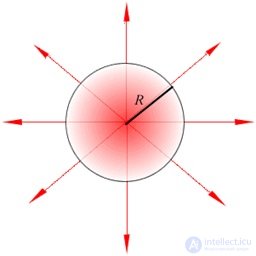
Рис. 1.41. Силовые линии электрического поля однородно заряженного шара
Не следует забывать, что по условию вне шара зарядов нет.
Поскольку в точке 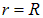 плотность заряда меняется скачком: предел «слева» отличен от нуля
плотность заряда меняется скачком: предел «слева» отличен от нуля 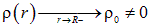 , а предел «справа» равен нулю
, а предел «справа» равен нулю 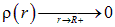 , вычисление придется проводить в два этапа: сначала для сферической поверхности радиуса
, вычисление придется проводить в два этапа: сначала для сферической поверхности радиуса 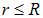 (она лежит внутри шара), а потом для сферической поверхности радиуса
(она лежит внутри шара), а потом для сферической поверхности радиуса 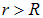 (она охватывает шар). В первом случае
(она охватывает шар). В первом случае
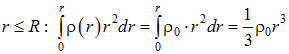 .
.
Соответственно, поле
|
|
(1.40) |
растет линейно с ростом расстояния до центра шара, что объясняется просто: площадь поверхности 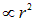 , а заряд внутри нее
, а заряд внутри нее 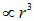
Во втором случае интеграл «обрезается сверху» при 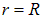 :
:
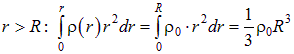
и поле
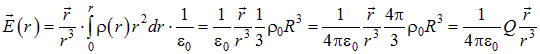 .
.
В последнем выражении учтено, что 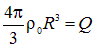 , где
, где 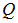 — полный заряд шара. Таким образом, вне шара его поле есть поле точечного заряда равного полному заряду шара и помещенного в центр этого шара:
— полный заряд шара. Таким образом, вне шара его поле есть поле точечного заряда равного полному заряду шара и помещенного в центр этого шара:
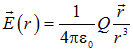 .
.
Оба выражения можно объединить в одну формулу. Если использовать полный заряд шара 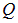 , получим:
, получим:
|
|
(1.41) |
Если вместо полного заряда шара 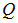 использовать в качестве параметр плотность заряда
использовать в качестве параметр плотность заряда 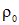 , эти формулы приобретут следующий вид (рис. 1.42):
, эти формулы приобретут следующий вид (рис. 1.42):
|
|
(1.42) |
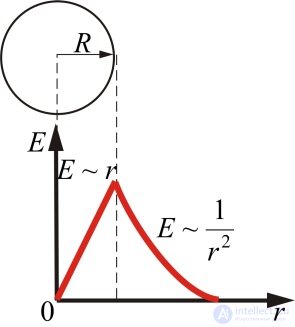
Рис. 1.42. Распределение напряженности электрического поля однородно заряженного шара
Формулы и выражают одну и ту же зависимость, их удобство определяется тем, какие параметры заданы: 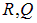 или
или  . Из этих формул наглядно видно, что на поверхности шара
. Из этих формул наглядно видно, что на поверхности шара 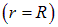 напряженность поля непрерывна, то есть не имеет разрыва. Это обусловлено тем, что в данном случае разрыв плотности заряда на поверхности шара первого рода — конечной величины: с
напряженность поля непрерывна, то есть не имеет разрыва. Это обусловлено тем, что в данном случае разрыв плотности заряда на поверхности шара первого рода — конечной величины: с 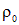 на нуль. Поэтому, как в , так и в в верхней и в нижней формулах поставлены знаки нестрогих неравенств. В каких случаях напряженность поля может терпеть разрыв, будет ясно из следующего примера.
на нуль. Поэтому, как в , так и в в верхней и в нижней формулах поставлены знаки нестрогих неравенств. В каких случаях напряженность поля может терпеть разрыв, будет ясно из следующего примера.
Потенциал поля легко найти, подставив, например, 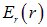 из в и выполнив интегрирование. Получаем:
из в и выполнив интегрирование. Получаем:
|
|
(1.43) |
где 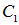 и
и 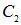 — постоянные интегрирования, которые находятся из следующих соображений. Константа
— постоянные интегрирования, которые находятся из следующих соображений. Константа 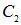 определяется из условия нормировки, например, на нуль на бесконечности
определяется из условия нормировки, например, на нуль на бесконечности
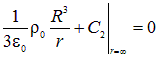
Откуда 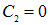 . Константа
. Константа 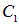 определяется из условия непрерывности потенциала на поверхности шара, то есть при
определяется из условия непрерывности потенциала на поверхности шара, то есть при 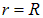 :
:
|
|
(1.44) |
или
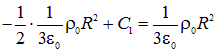
откуда
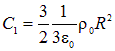
Отметим, что требование непрерывности потенциала нередко называют «сшивкой» двух решений на границе раздела. В данном случае это граница раздела двух областей: областью, где есть заряд (внутри шара), и областью, где его нет (вне шара). Уже сейчас можно отметить, что потенциал непрерывен во всех случаях, кроме одного: так называемого «двойного слоя». Представьте поверхность, по одной стороне которой с плотностью 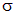 распределен положительный заряд, а по другой стороне которой с плотностью
распределен положительный заряд, а по другой стороне которой с плотностью 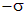 распределен отрицательный заряд. Такая поверхность и называется двойным слоем, на этой поверхности потенциал терпит разрыв. Такую (плоскую) поверхность можно получить, неограниченно сближая две обкладки плоского конденсатора. То же самое можно проделать для конденсатора любой формы, например, сферического или цилиндрического. Во всех остальных случаях потенциал непрерывен.
распределен отрицательный заряд. Такая поверхность и называется двойным слоем, на этой поверхности потенциал терпит разрыв. Такую (плоскую) поверхность можно получить, неограниченно сближая две обкладки плоского конденсатора. То же самое можно проделать для конденсатора любой формы, например, сферического или цилиндрического. Во всех остальных случаях потенциал непрерывен.
Подставляя полученные значения констант интегрирования в , запишем окончательный результат в виде
|
|
(1.45) |
При такой нормировке потенциал в центре шара отличен от нуля и равен
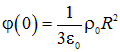 .
.
Полученные результаты иллюстрирует приведенный ниже рисунок 1.43.
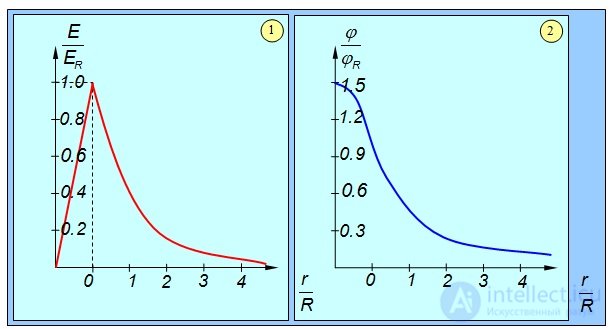
Рис. 1.43. Напряженность (1) и потенциал (2) электрического поля равномерно заряженного шара радиусом R в единицах напряженности и потенциала на его поверхности (r = R)
Поле равномерно заряженной сферической поверхности
В данном случае равномерного распределения заряда по сферической поверхности, как и в предыдущем, имеет место сферическая симметрия, поэтому общие формулы, полученные выше, применимы и здесь. Однако относиться к ним необходимо с известной осторожностью по следующей причине. Входящая в правую часть объемная плотность заряда ведет себя в данном случае следующим интересным образом:

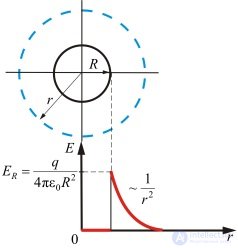
Рис. 1.44. Напряженность электрического поля равномерно заряженной сферы
Действительно, заряд имеется только на поверхности, то есть при 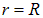 , всюду внутри, то есть при
, всюду внутри, то есть при 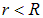 и всюду снаружи, то есть при
и всюду снаружи, то есть при 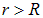 зарядов нет. То, что объемная плотность заряда
зарядов нет. То, что объемная плотность заряда 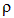 в точках поверхности
в точках поверхности 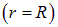 обращается в бесконечность (+∞ в случае положительного заряда и –∞ в случае отрицательного) можно показать следующим образом. На рисунке рядом изображен участок некоторой поверхности, по которой с поверхностной плотностью
обращается в бесконечность (+∞ в случае положительного заряда и –∞ в случае отрицательного) можно показать следующим образом. На рисунке рядом изображен участок некоторой поверхности, по которой с поверхностной плотностью 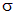 распределен заряд. Для определения величины объемной плотности заряда в некоторой точке поверхности рассмотрим цилиндр (рис. 1.45), верхнее основание которого находится над поверхностью, а нижнее — под поверхностью. Площадь оснований цилиндра равна
распределен заряд. Для определения величины объемной плотности заряда в некоторой точке поверхности рассмотрим цилиндр (рис. 1.45), верхнее основание которого находится над поверхностью, а нижнее — под поверхностью. Площадь оснований цилиндра равна 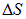 , высота —
, высота — 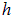 , объем
, объем 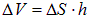 . Заряд внутри цилиндра
. Заряд внутри цилиндра 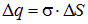 , объемная плотность заряда по определению равна пределу отношения заряда, находящегося внутри некоторого объема, к величине этого объема при стремлении последнего к нулю (со всеми оговорками относительно объема «физически бесконечно малого»). Получаем
, объемная плотность заряда по определению равна пределу отношения заряда, находящегося внутри некоторого объема, к величине этого объема при стремлении последнего к нулю (со всеми оговорками относительно объема «физически бесконечно малого»). Получаем
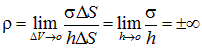
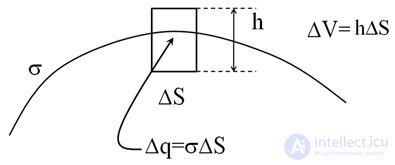
Рис. 1.45. Плотность заряда на поверхности
Важно, что плотность на поверхности равна бесконечности. Функции такого рода (везде, кроме одной точки — нуль, а в этой единственной точке — бесконечность) относятся к классу так называемых обобщенных функций, называются функциями Дирака в честь физика Дирака, впервые введшего в обиход физики такую функцию для удовлетворения нужд квантовой механики. Мы не будем здесь подробно исследовать и использовать в расчетах такого рода функции. Наша цель показать, что рассмотрение формально бесконечно тонких заряженных поверхностей приводит к появлению у объемной плотности заряда разрывов (бесконечных), что, в свою очередь, порождает бесконечные разрывы на такой заряженной поверхности у напряженности электрического поля. Подчеркнем, что потенциал поля при этом остается непрерывным.
Выход из положения прост. При всех 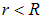 используем первую из формул с
используем первую из формул с 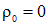 , получаем, что всюду внутри однородно заряженной сферической оболочки поле отсутствует:
, получаем, что всюду внутри однородно заряженной сферической оболочки поле отсутствует: 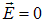 . При всех
. При всех 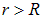 справедлива вторая формула из . Как и в случае однородно по объему заряженного шара, вне однородно заряженной сферической оболочки, ее поле есть поле точечного заряда, помещенного в центр этой оболочки и равного ее полному заряду. В данном случае, разумеется
справедлива вторая формула из . Как и в случае однородно по объему заряженного шара, вне однородно заряженной сферической оболочки, ее поле есть поле точечного заряда, помещенного в центр этой оболочки и равного ее полному заряду. В данном случае, разумеется 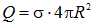 .
.
Окончательный результат такой:
|
|
(1.46) |
На самой сферической поверхности напряженность поля в этом случае терпит разрыв. Зависимость радиальной компоненты поля от расстояния до центра сферической поверхности показана на рис. 1.46.
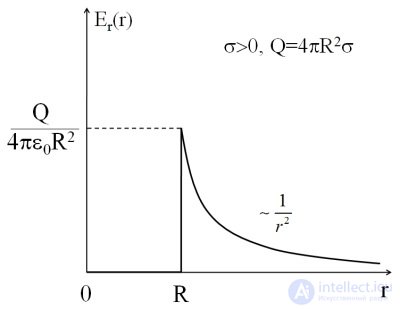
Рис. 1.46. Зависимость поля от расстояния до центра сферической оболочки
Зависимость потенциала от расстояния до центра сферической оболочки можно получить, интегрируя . При нормировке на нуль на бесконечности результат выглядит следующим образом:
|
|
(1.47) |
Зависимость показана на рис. 1.47.
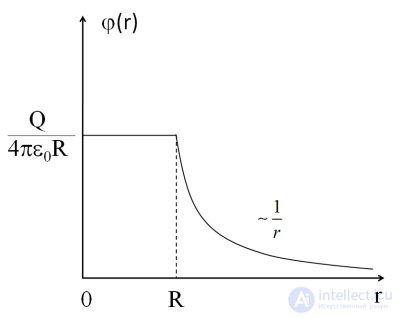
Рис. 1.47. Потенциал равномерно заряженной сферы
Однородное (равномерное) распределение заряда по бесконечно длинной цилиндрической поверхности (рис. 1.48) обладает цилиндрической, трансляционной и зеркальной симметрией. Это означает следующее. При повороте такого распределения заряда вокруг оси цилиндрической поверхности на любой угол оно совпадает само с собой. При сдвиге (переносе, трансляции) такого распределения заряда на любое расстояние вдоль оси симметрии оно также совпадает само с собой. И, наконец, если через любую точку на оси симметрии провести плоскость перпендикулярную к оси, и отразить в этой плоскости как в зеркале «верхнюю» часть распределения заряда, то отражение «верхней» части совпадет с «нижней» и наоборот, отражение «нижней» совпадет с «верхней». Другими словами, это распределение заряда инвариантно относительно указанных преобразований. Следовательно, и создаваемое этим распределением заряда электрическое поле должно быть инвариантно (совпадать само с собой) при указанных преобразованиях.
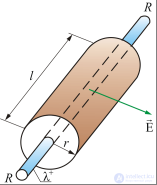
Рис. 1.48. Бесконечно длинная цилиндрическая поверхность
Введем цилиндрическую систему координат: ось 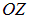 направим по оси симметрии,
направим по оси симметрии, 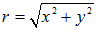 — расстояние до оси симметрии,
— расстояние до оси симметрии, 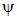 — азимутальный угол, угол поворота вокруг оси симметрии,
— азимутальный угол, угол поворота вокруг оси симметрии, 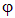 — по-прежнему потенциал поля.
— по-прежнему потенциал поля.
Из свойств симметрии вытекает, что потенциал поля не может зависеть ни от координаты 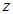 — нарушится трансляционная симметрия, ни от координаты
— нарушится трансляционная симметрия, ни от координаты 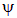 — нарушится осевая (цилиндрическая) симметрия. Остается только зависимость от
— нарушится осевая (цилиндрическая) симметрия. Остается только зависимость от 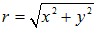 — расстояния до оси цилиндра. Таким образом:
— расстояния до оси цилиндра. Таким образом:
|
|
продолжение следует...
Часть 1 1. Электрическое поле в вакууме
Часть 2 1.3. Электрическое поле. Напряженность и потенциал поля - 1. Электрическое
Часть 3 - 1. Электрическое поле в вакууме
Часть 4 1.4. Поток вектора. Теорема Остроградского-Гаусса для вектора - 1. Электрическое
Часть 5 1.5. Применение теоремы Гаусса для расчетов напряженности электрического поля -
Часть 6 Дополнения - 1. Электрическое поле в вакууме
Часть 7 Дополнение 2. Сила взаимодействия систем непрерывно распределенных зарядов - 1.
Комментарии
Оставить комментарий
Базовая физика
Термины: Базовая физика