- 1. Электрическое поле в вакууме

Отсюда находим заряд капельки

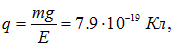
то есть капелька несла пять электронных зарядов. Именно в таких экспериментах было обнаружено квантование электрического заряда и определена его минимальная величина e.

Движением заряженных частиц можно управлять, с помощью электрического поля нужной величины и направления. Так происходит, например, в электроннолучевой трубке осциллографа.

На рис. 1.24 показывается движение электронного луча, рисующего на экране электроннолучевой трубки с электрическим отклонением синусоиду. В осциллографе на вертикальные отклоняющие пластины подан усиленный исследуемый сигнал, а на горизонтальные — пилообразное напряжение развертки. В результате электронный луч «рисует» зависимость исследуемого сигнала от времени на экране осциллографа.

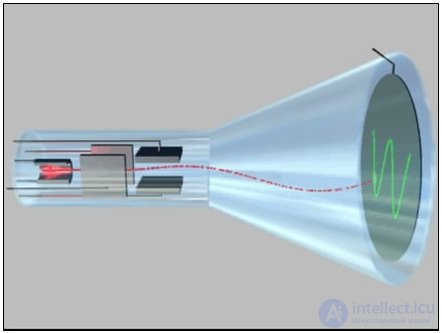
Рис. 1.24. Принцип действия электроннолучевой трубки

Определение напряженности поля очень часто используется в виде

В силу определения (или, очевидным образом, это одно и то же) напряженность электрического поля называют его силовой характеристикой — оно определяет силу, действующую на заряд, помещенный в поле.

Пример 5. В пространство между пластинами плоского конденсатора влетает частица, движущаяся параллельно пластинам вдоль оси конденсатора (рис. Об этом говорит сайт https://intellect.icu . 1.25). Начальную кинетическую энергию частица получила, пройдя ускоряющую разность потенциалов Под действием поля конденсатора частица отклоняется к одной из пластин (в зависимости от знака заряда) и в конечном итоге попадает на нее. Это расстояние 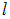можно измерить. Известно также расстояние между пластинами и напряжение 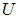на конденсаторе. Можно ли по этим данным установить тип частицы (найдя ее удельный заряд, т. е. отношение заряда к массе )?

Решение. Решим задачу сначала методом размерностей. Пройденное расстояние должно быть функцией параметров задачи:

Вспоминая, что произведение потенциала на заряд дает энергию, размерность которой 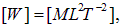получаем

Рис. 1.25. движение заряженной частицы между пластинами плоского конденсатора

Подставляя эту размерность, получаем уравнение:

Сравнивая размерности в обеих частях равенства, приходим к уравнениям:

Последнее уравнение, следующее из отсутствия в левой части величины размерности времени, сразу дает нам или После этого немедленно находим: Подставляя найденные значения, получаем:

Произвольная степень (показатель степени b определить не удалось) означает, что результат зависит от произвольной функции безразмерного отношения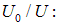

Вид этой функции мы пока не знаем: если в задачу входят величины одинаковой размерности, то функцию их отношения с помощью анализа размерности найти, естественно, не удастся. Но мы уже можем ответить на вопрос задачи: в ответ не вошли параметры, характеризующие частицу — ни ее масса, ни ее заряд. Все частицы при заданных условиях будут отклоняться одинаково, и использовать такой прибор для их идентификации нельзя.

Приведем теперь точное решение задачи. Начальную скорость частицы находим из соотношения

В конденсаторе частица находится под действием электрического поля 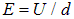и приобретает поперечное ускорение Расстояние 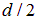до попадания на пластину она пройдет за время t:

откуда находим время полета:

В продольном же направлении за это время частица пролетит расстояние

Мы приходим к тому же выводу о независимости от характеристик частицы. К тому же, теперь найдена функция 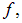оставшаяся не определенной в нашем предварительном результате.

В Главе 4 раздела «Механика» было показано, что консервативная сила связана с потенциальной энергией 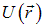соотношением

Здесь знак — общепринятое обозначение векторного оператора «набла», результат действия которого на скалярную функцию координат есть градиент этой функции. Явный вид оператора набла в декартовых координатах следующий:

Подставив в 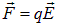и разделив на , получаем

Скалярная функция называется потенциалом электрического поля.

Как видно из (1.13), потенциальная энергия точечного заряда 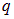в поле с потенциалом равна

а действующая на него сила

В Дополнении 3 разобран пример использования этих соотношений.

Напряженность поля определяет силу, действующую в поле на точечный заряд, а потенциал — его потенциальную энергию в этом поле. Поэтому, следуя смыслу соотношений и, напряженность электрического поля 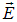называют силовой характеристикой поля, а потенциал 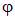— его энергетической характеристикой.

Как и потенциальная энергия, потенциал поля всегда определен с точностью до аддитивной постоянной. Это видно из : поскольку набла есть дифференциальный оператор, потенциалы 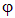и 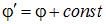физически тождественны, так как им соответствует поле одной и той же напряженности

.

Это позволяет нормировать потенциал, произвольно выбирая некоторую точку 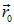и полагая потенциал в этой точке равным нулю

Учитывая, что и напряженность поля, и потенциал поля убывают с ростом расстояния до системы зарядов, создающей поле, во всех тех случаях, когда конечный заряд распределен по конечной области пространства, нормировать потенциал естественно и удобно на «нуль на бесконечности», то есть полагать его равным нулю на бесконечном удалении от системы зарядов

О тех идеализированных случаях, когда нормировка на нуль на бесконечности, именно в силу идеализированности задачи, лишена смысла, будет сказано далее.

Соотношение (1.13) позволяет вычислить напряженность поля по известному потенциалу;

Получим «обратную» связь: выразим потенциал поля через его напряженность. Для этого сравним три выражения: выражение для из (1.18), выражение для вектора бесконечно малого перемещения 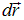и выражение для полного дифференциала функции :

Нетрудно видеть, что скалярное произведение двух первых векторов равно полному дифференциалу потенциала

или, с учетом

На самом деле это соотношение не новое. Если умножить (1.20) на заряд 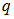и учесть связи (1.14) и (1.15), мы получим знакомое по главе 4 раздела «Механика» соотношение, связывающее работу консервативной силы и убыль потенциальной энергии

.

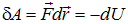Там же, в разделе «Механика» было показано, что стационарное потенциальное поле консервативно. Из соотношения (1.18) вытекает, что электростатическое поле консервативно во всех тех случаях, когда потенциал поля не зависит от времени.

Интегрируя соотношение (1.20) от точки 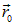, потенциал в которой принят равным нулю, до некоторой точки 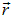, потенциал в которой нас интересует, вдоль произвольной, удобной для вычислений кривой (поле консервативно и от формы кривой результат не зависти), получаем

Вычислим с помощью (1.21) потенциал поля точечного заряда 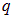, находящегося в начале координат, нормировав его на нуль на бесконечном удалении от этого заряда. Воспользуемся для этого законом Кулона в форме (1.9):

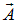При вычислении использовано тождество , справедливое для любого вектора : и являющееся результатом простого дифференцирования определения модуля любого вектора: .

Таким образом, потенциал поля точечного заряда находящегося в начале координат имеет вид

и поле это, как уже отмечалось ранее, центральное: фактически потенциал поля зависит только от .

Учитывая, что стоящей в знаменателе модуль радиус-вектора есть ни что иное как расстояние от заряда, создающего поле до точки наблюдения поля, формулу легко обобщить на случай, когда заряд находится не в начале координат, а в точке с радиус-вектором . В этом случае расстояние от заряда до точки наблюдения поля равно и потенциал поля в точке (при прежней нормировке на нуль на бесконечности) равен

Связь между напряженностью поля и его потенциалом линейная, поэтому принцип суперпозиции для напряженности поля справедлив и для потенциала поля. Другими словами: потенциал поля системы зарядов равен алгебраической сумме потенциалов поля от каждого из зарядов системы. Используя принцип суперпозиции, потенциал поля системы зарядов можно написать сразу :

Здесь — полное число зарядов в системе.

В случае непрерывного распределения заряда по некоторому объему , получим

При непрерывном распределении заряда по некоторой поверхности или кривой , получим соответственно

где и 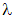— соответствующие поверхностная и линейная плотности.

В Дополнении 4 разобран пример использования только что полученных соотношений.

Мы не будем рассматривать здесь отдельно вопрос о работе электростатических сил при перемещении в электростатическом поле точечных зарядов и заряженных тел. Электростатическое поле консервативно (рис. 1.26), потенциальная энергия заряда в поле равна 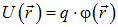, поэтому работа электростатических сил всегда может быть вычислена с помощью соотношений вида

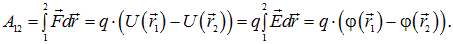
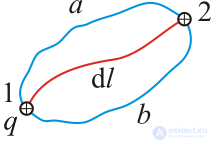
Рис. 1.26. Работа электростатических сил зависит только от положения начальной и конечной точек

Вычислим энергию взаимодействия зарядов, входящих с состав некоторой системы.

Для нумерации этих зарядов удобно использовать два индекса, например, и . Одни и те же заряды системы, один раз это , другой раз это . Подчеркнем, что заряд 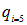и заряд 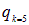это один и тот же 5-ый заряд системы. Такие «сложности» необходимы для компактной записи выражения для их энергии взаимодействия и вот почему. Заряды взаимодействуют попарно, энергия взаимодействия и зарядов согласно равна

Здесь — потенциал 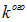заряда в той точке, где находится заряд.

В — взаимодействие заряда самого с собой или его потенциальную энергию в собственном поле мы не рассматриваем.

Поэтому при суммировании энергий попарного взаимодействия зарядов мы обязательно должны учесть, что , во-первых, и, во вторых, каждая пара зарядов должна присутствовать в сумме только один раз. Это можно сделать