Лекция
Это продолжение увлекательной статьи про электрическое поле в вакууме.
...
двумя способами. Первый состоит в том, что при записи двойной суммы, явно оговаривается, например, что 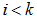 :
:
|
|
(1.29) |
При втором способе, при соблюдении неравенства 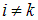 , суммирование ведется по всем возможным значениям
, суммирование ведется по всем возможным значениям 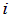 и
и 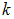 , соответственно, слагаемое, отвечающее взаимодействию одной и той же пары зарядов присутствует в сумме дважды, поэтому сумму необходимо разделить на 2. Получается:
, соответственно, слагаемое, отвечающее взаимодействию одной и той же пары зарядов присутствует в сумме дважды, поэтому сумму необходимо разделить на 2. Получается:
|
|
(1.30) |
В случае непрерывного распределения заряда по некоторому объему 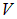 с плотностью
с плотностью  , соотношение, к примеру, принимает вид:
, соотношение, к примеру, принимает вид:
|
|
(1.31) |
В первой из формул в (1.31) 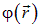 — потенциал всех зарядов кроме
— потенциал всех зарядов кроме 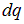 в той точке
в той точке  , в которой находится
, в которой находится 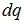 , во втором соотношении этот потенциал выписан явно, в третьей выполнена следующая операция: два интеграла, для краткости объединены в один и заряды
, во втором соотношении этот потенциал выписан явно, в третьей выполнена следующая операция: два интеграла, для краткости объединены в один и заряды 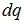 и
и 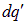 выражены через плотность заряда
выражены через плотность заряда 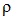 .
.
Мы не выписываем здесь формулы для случаев распределения заряда по поверхности или вдоль некоторой кривой, они лишь требуют замены в 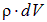 на
на 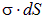 и
и  .
.
Для наглядного представления распределения потенциала в пространстве используются эквипотенциальные поверхности.
|
Эквипотенциальная поверхность (поверхность равного потенциала) — это совокупность точек, имеющих равный потенциал. |
Рассмотрим картину эквипотенциальных поверхностей некоторых полей.
Напомним, что как из физических соображений, так и непосредственно из соотношения 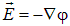 вытекает взаимная ортогональность силовых линий и эквипотенциальных поверхностей. Действительно, согласно определению, уравнение эквипотенциальной поверхности имеет вид
вытекает взаимная ортогональность силовых линий и эквипотенциальных поверхностей. Действительно, согласно определению, уравнение эквипотенциальной поверхности имеет вид
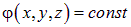
Дифференцируя это соотношение, получаем
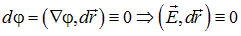
для всех перемещений 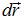 , касательных к эквипотенциальной поверхности. Значит вектор
, касательных к эквипотенциальной поверхности. Значит вектор 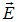 перпендикулярен эквипотенциальной поверхности. Осталось вспомнить, что вектор
перпендикулярен эквипотенциальной поверхности. Осталось вспомнить, что вектор 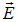 направлен по касательной к силовой линии по определению. Утверждение об ортогональности силовых линий и эквипотенциальных поверхностей доказано.
направлен по касательной к силовой линии по определению. Утверждение об ортогональности силовых линий и эквипотенциальных поверхностей доказано.
Эквипотенциальные поверхности поля точечного заряда представляют собой концентрические сферы с центром в точке нахождения заряда (см. рис. 1.27). Эквипотенциальные поверхности обозначены сплошными синими линиями, силовые линии — красными пунктирными линиями.
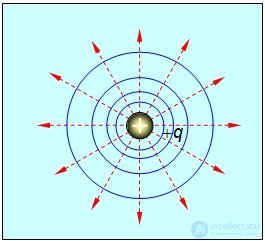
Рис. 1.27. Эквипотенциальные поверхности (сферы) (сплошные линии синего цвета) и силовые линии (пунктирные линии красного цвета) поля точечного заряда
Эквипотенциальные поверхности однородного электрического поля представляют собой плоскости, перпендикулярные силовым линиям и расположенные на одинаковом расстоянии друг от друга (см. рис. 1.28).
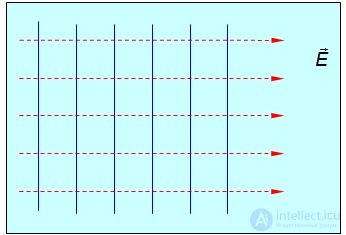
Рис. 1.28. Эквипотенциальные поверхности однородного электрического поля
Эквипотенциальные поверхности поля двух одноименных одинаковых точечных зарядов представлены на рис. 1.29.
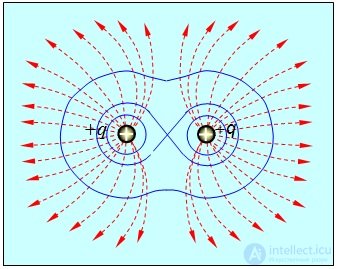
Рис. 1.29. Эквипотенциальные поверхности двух одноименных одинаковых точечных зарядов
Эквипотенциальные поверхности поля двух разноименных одинаковых по модулю точечных зарядов представлены на рис. 1.30.
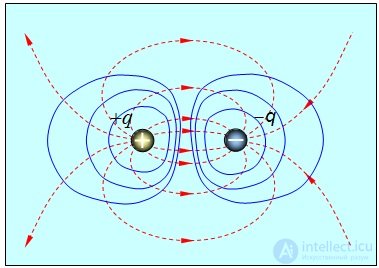
Рис. 1.30. Эквипотенциальные поверхности двух разноименных одинаковых по модулю точечных зарядов
Графический вид двумерного (в плоскости z = 0) потенциала электрического поля, создаваемого точечным зарядом, расположенным в начале координат, показан на рис. 1.31.

Рис. 1.31. Вид двумерного (в плоскости z = 0) кулоновского потенциала 1/r вблизи положительного (1) и отрицательного (2) точечного зарядов. В случае (1) положительный пробный заряд натыкается на бесконечно высокий потенциальный барьер, препятствующий проникновению к центру. В случае (2) на пробный заряд действует сила притяжения, и он стремится скатиться в образовавшуюся потенциальную яму
Экспериментальное исследование потенциала поля вокруг заряженного металлического шара с помощью «пламенного» зонда показано на рис. 1.32. Используемый зонд присоединен к электрометру. Для выравнивания потенциала зонда с потенциалом той точки, где он находится, измерительный зонд помещается в пламя небольшой газовой горелки, обеспечивающей ионизацию воздуха и возможность стекания и натекания зарядов на зонд. Демонстрируется уменьшение потенциала при перемещении зонда по радиусу от центра шара и постоянство потенциала при движении зонда по окружности вокруг центра заряженного шара.

Рис. 1.32. Экспериментальное исследование потенциала поля вокруг заряженного металлического шара с помощью «пламенного» зонда
В Дополнении 7 получено полезное соотношение для градиента скалярной функции, зависящей только от модуля радиус-вектора.
Теорема установлена М.В. Остроградским (рис. 1.33) в виде общей математической теоремы для любого векторного поля и К. Гауссом — применительно к электростатическому полю.

Рис. 1.33. М. Острогра́дский (1801–1861) — российский математик и механик
Закон Кулона и принцип суперпозиции позволяют вычислить потенциал поля любого распределения заряда
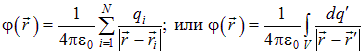 .
.
Используя связь 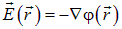 или непосредственно с помощью закона Кулона и принципа суперпозиции, можно вычислить и напряженность поля
или непосредственно с помощью закона Кулона и принципа суперпозиции, можно вычислить и напряженность поля
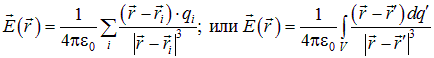
Однако, практическое вычисление написанных выше сумм и интегралов далеко не всегда так просто, как просто выглядят сами суммы и интегралы. Они вычисляются достаточно непринужденно, когда зарядов два, три, может быть, десяток. Если же речь идет о макроскопических заряженных телах, когда число точечных зарядов (протонов, электронов и т. п.) макроскопически велико, прямое вычисление подобных выражений становится очень сложной задачей. В первую очередь это касается написанных выше сумм, а не интегралов.
Мы хотим подчеркнуть, что при решении макроскопических задач, в подавляющем большинстве случаев, можно считать, что заряд распределен непрерывно, соответственно, вычислять надо не суммы, а интегралы. Поэтому встает задача: на базе закона Кулона и принципа суперпозиции, написать интегральные и/или дифференциальные уравнения, которым удовлетворяет напряженность поля произвольного распределения зарядов. Эту задачу в ряде случаев успешно решает обсуждаемая в этом параграфе теорема Гаусса для вектора 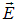 .
.
Рассмотрим некоторую поверхность  и на ней бесконечно малый участок (бесконечно малую площадку) площадью
и на ней бесконечно малый участок (бесконечно малую площадку) площадью 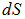 (рис. 1.34).
(рис. 1.34).
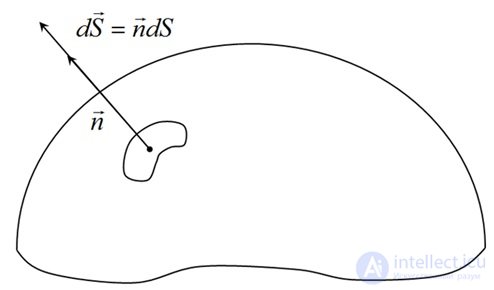
Рис. 1.34. Бесконечно малый участок поверхности
Показанный на рисунке «вектор площадки» 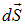 имеет следующий смысл: 1) он направлен по нормали
имеет следующий смысл: 1) он направлен по нормали 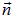 к поверхности
к поверхности 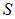 в той ее точке, в окрестности которой находится площадка; 2) его модуль равен площади площадки
в той ее точке, в окрестности которой находится площадка; 2) его модуль равен площади площадки 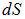 . Вектор
. Вектор 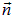 , а вместе с ним и вектор
, а вместе с ним и вектор 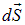 всегда направлены по перпендикуляру к поверхности в данном ее месте, а вот в какую сторону: налево вверх, как на рисунке выше, или в противоположную сторону (направо вниз, «под» поверхность), — в общем случае это дело произвольного выбора. Однако в ряде случаев, по умолчанию, действуют определенные правила. Например, если поверхность замкнутая, то есть представляет собой некоторую замкнутую «оболочку», то по умолчанию берется «внешняя» нормаль, направленная наружу. Выбор «внутренней» нормали ничему не противоречит, но должен быть специально оговорен. Если поверхность не замкнутая и опирается на некоторый контур, а, кроме того, задано направление обхода этого контура, то направление нормали общепринято связывать с направлением обхода правилом правого винта. С той же оговоркой, что и выше: направление обхода контура и направление нормали к поверхности, которая на него опирается, можно связать, используя левый, а не правый винт, такой выбор ничему не противоречит, но должен быть специально оговорен. Здесь и ниже, если иное специально не оговорено, будут использоваться указанные выше общепринятые правила: внешняя нормаль и правый винт.
всегда направлены по перпендикуляру к поверхности в данном ее месте, а вот в какую сторону: налево вверх, как на рисунке выше, или в противоположную сторону (направо вниз, «под» поверхность), — в общем случае это дело произвольного выбора. Однако в ряде случаев, по умолчанию, действуют определенные правила. Например, если поверхность замкнутая, то есть представляет собой некоторую замкнутую «оболочку», то по умолчанию берется «внешняя» нормаль, направленная наружу. Выбор «внутренней» нормали ничему не противоречит, но должен быть специально оговорен. Если поверхность не замкнутая и опирается на некоторый контур, а, кроме того, задано направление обхода этого контура, то направление нормали общепринято связывать с направлением обхода правилом правого винта. С той же оговоркой, что и выше: направление обхода контура и направление нормали к поверхности, которая на него опирается, можно связать, используя левый, а не правый винт, такой выбор ничему не противоречит, но должен быть специально оговорен. Здесь и ниже, если иное специально не оговорено, будут использоваться указанные выше общепринятые правила: внешняя нормаль и правый винт.
Введем в рассмотрение поток  произвольного вектора
произвольного вектора 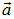 через выбранную площадку. По определению:
через выбранную площадку. По определению:
|
Поток
|
Формально рассматривается бесконечно малая площадка, фактически (например, при численном суммировании) она должна быть настолько мала, чтобы в ее пределах вектор 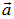 можно было считать неизменным (однородным), а саму площадку плоской, тогда не возникает проблемы, в какой точке внутри площадки проводить нормаль к ней.
можно было считать неизменным (однородным), а саму площадку плоской, тогда не возникает проблемы, в какой точке внутри площадки проводить нормаль к ней.
Для общности определения (в физике рассматриваются потоки и других векторов) выше был рассмотрен произвольный вектор 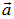 , применительно к вектору напряженности электрического поля
, применительно к вектору напряженности электрического поля 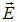 , с учетом замечания о размерах площадки, определение потока иллюстрирует рис. 1.35.
, с учетом замечания о размерах площадки, определение потока иллюстрирует рис. 1.35.
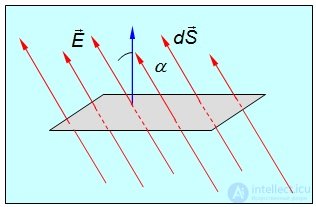
Рис. 1.35. Поток вектора напряженности электрического поля через бесконечно малую площадку
Согласно определению, поток вектора напряженности через площадку равен (здесь и в дальнейшем, для краткости, когда это будет удобным, будем писать: «площадка» и указывать при этом вектор этой площадки, которым полностью определены и ее площадь и ориентация):
|
|
(1.43) |
где α — угол между векторами 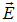 и
и  ,
, 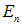 — нормальная к поверхности составляющая вектора
— нормальная к поверхности составляющая вектора 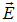 . Подчеркнем, что изменение направления нормали
. Подчеркнем, что изменение направления нормали  как и изменение направления вектора напряженности на обратное меняет знак потока на противоположный, таким образом, поток вектора - величина алгебраическая.
как и изменение направления вектора напряженности на обратное меняет знак потока на противоположный, таким образом, поток вектора - величина алгебраическая.
Поток вектора 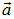 через произвольную поверхность S равен сумме потоков через все площадки, на которые разбита поверхность S, то есть интегралу по этой поверхности вида:
через произвольную поверхность S равен сумме потоков через все площадки, на которые разбита поверхность S, то есть интегралу по этой поверхности вида:
|
|
(1.32) |
Если векторное поле 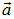 однородно, то есть
однородно, то есть 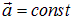 , а поверхность плоская, то
, а поверхность плоская, то
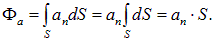
Здесь S — площадь этой поверхности. Для обозначения интеграла по замкнутой поверхности используется специальный значок интеграла, а именно: с кружком в середине (S — замкнутая поверхность) (рис. 1.36):
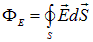
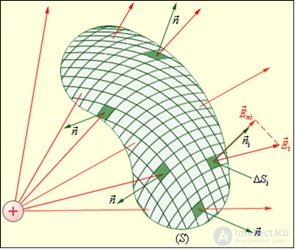
Рис. 1.36. Поток вектора напряженности электрического поля через замкнутую поверхность
Для уяснения смысла такой величины как поток вектора весьма полезно, в силу наглядности, рассмотрение потока жидкости, например, в реке или в трубе.
Пусть, для простоты несжимаемая жидкость, с плотностью 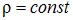 течет со скоростью
течет со скоростью 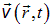 . Указание зависимости вектора скорости от координат точки и времени означает задание векторного поля, в данном случае: поля вектора скорости
. Указание зависимости вектора скорости от координат точки и времени означает задание векторного поля, в данном случае: поля вектора скорости  . Как и всякое векторное поле, поле скоростей удобно изобразить с помощью линий поля, которые в данном случае принято называть «линиями тока». По определению, в любой точке вектор скорости жидкости направлен по касательной к линии тока. Выделим внутри жидкости площадку
. Как и всякое векторное поле, поле скоростей удобно изобразить с помощью линий поля, которые в данном случае принято называть «линиями тока». По определению, в любой точке вектор скорости жидкости направлен по касательной к линии тока. Выделим внутри жидкости площадку 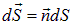 (см. рис. 1.37) настолько малую, что скорость
(см. рис. 1.37) настолько малую, что скорость 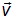 во всех точках этой площадки можно считать одной и той же. Возьмем временной интервал
во всех точках этой площадки можно считать одной и той же. Возьмем временной интервал 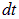 настолько малый, что скорость
настолько малый, что скорость 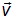 за это время сколько-нибудь заметно измениться не успевает и поставим такой вопрос: «Какая масса
за это время сколько-нибудь заметно измениться не успевает и поставим такой вопрос: «Какая масса 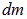 жидкости протекает сквозь площадку
жидкости протекает сквозь площадку 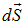 за время
за время 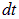 ?». Очевидно, что за указанное время сквозь площадку пройдут те частицы жидкости, которые были от нее не дальше (вдоль потока), чем на расстоянии
?». Очевидно, что за указанное время сквозь площадку пройдут те частицы жидкости, которые были от нее не дальше (вдоль потока), чем на расстоянии  . Более дальние, имея скорость
. Более дальние, имея скорость 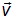 , просто не успеют «добраться» до площадки за интересующее нас время
, просто не успеют «добраться» до площадки за интересующее нас время 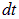 .
.
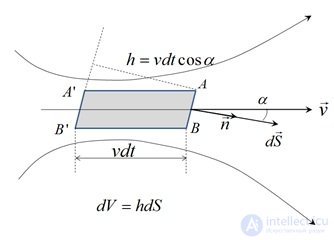
Рис. 1.37. К выводу соотношения для потока вектора
На рисунке выше жидкость, которая успеет за время 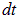 пересечь площадку
пересечь площадку 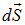 , занимает заштрихованный объем
, занимает заштрихованный объем 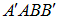 , величина которого, как видно из рисунка равна
, величина которого, как видно из рисунка равна 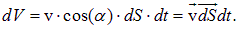 . Соответственно, масса жидкости проходящей сквозь площадку
. Соответственно, масса жидкости проходящей сквозь площадку 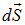 за время
за время 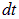 равна
равна
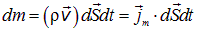 , где
, где 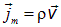
В написанной выше формуле вектор 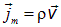 есть характеристика именно потока жидкости, определяемая ее плотностью и скоростью течения. Величины
есть характеристика именно потока жидкости, определяемая ее плотностью и скоростью течения. Величины 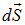 и
и 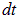 являются параметрами "постановки эксперимента". При том же потоке жидкости можно рассмотреть другую площадку и выбрать другое время регистрации массы. Вектор
являются параметрами "постановки эксперимента". При том же потоке жидкости можно рассмотреть другую площадку и выбрать другое время регистрации массы. Вектор 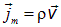 называется вектором плотности потока массы. Единица его измерения
называется вектором плотности потока массы. Единица его измерения 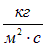 наглядно демонстрирует его физический смысл: величина вектора показывает, сколько килограмм жидкости протекает за секунду через квадратный метр площадки перпендикулярной потоку. Такой же смысл имеют его проекции на оси, с тем отличием, что
наглядно демонстрирует его физический смысл: величина вектора показывает, сколько килограмм жидкости протекает за секунду через квадратный метр площадки перпендикулярной потоку. Такой же смысл имеют его проекции на оси, с тем отличием, что 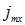 численно равно массе жидкости протекающей за секунду сквозь квадратный метр площадки перпендикулярной оси ОХ,
численно равно массе жидкости протекающей за секунду сквозь квадратный метр площадки перпендикулярной оси ОХ, 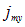 – … оси ОУ и так далее.
– … оси ОУ и так далее.
Если разделить 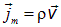 на плотность
на плотность 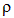 получится
получится 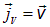 — вектор плотности потока объема, измеряемый в
— вектор плотности потока объема, измеряемый в 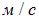 . Модуль этого вектора численно равен числу кубометров жидкости проходящих за секунду сквозь квадратный метр площадки перпендикулярной потоку жидкости. Знание этого вектора требуется, например, при расчете пропускной способности газо- или нефтепровода, как впрочем, и водопровода.
. Модуль этого вектора численно равен числу кубометров жидкости проходящих за секунду сквозь квадратный метр площадки перпендикулярной потоку жидкости. Знание этого вектора требуется, например, при расчете пропускной способности газо- или нефтепровода, как впрочем, и водопровода.
Доказанная ниже теорема Гаусса для вектора 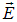 (см. соотношение ) показывает, что источниками электростатического поля являются электрические заряды.
(см. соотношение ) показывает, что источниками электростатического поля являются электрические заряды.
Рассмотрим для начала частный, но очень простой, пример прямого вычисления потока вектора через поверхность.
Пример 6. Полусфера радиусом R с плоским основанием помещена в постоянное однородное электрическое поле E, перпендикулярное основанию полусферы (рис. 1.38). Найти поток вектора напряженности через основание полусферы, саму полусферу и через всю замкнутую поверхность этого тела.
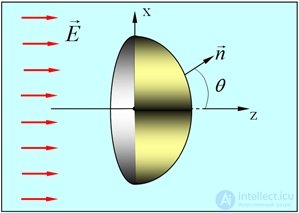
Рис. 1.38. Пример расчета потока вектора напряженности электрического поля
Решение. Проще всего рассчитать поток 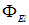 через основание полусферы. Направим ось z вдоль поля. Направление вектора внешней нормали к основанию обратно направлению вектора E. При этом вектор E одинаков во всех точках основания. Поток через основание получается равным взятому с обратным знаком произведению E на площадь основания
через основание полусферы. Направим ось z вдоль поля. Направление вектора внешней нормали к основанию обратно направлению вектора E. При этом вектор E одинаков во всех точках основания. Поток через основание получается равным взятому с обратным знаком произведению E на площадь основания
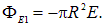
Найдем теперь поток напряженности через поверхность полусферы. Используя сферические координаты — углы  и
и 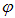 — для определения положения точки на полусфере, мы видим, что
— для определения положения точки на полусфере, мы видим, что
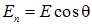
и
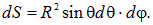
Поэтому поток через элементарную площадку на полусфере равен
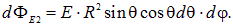
Учитывая, что
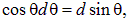
а
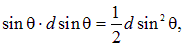
записываем поток в виде
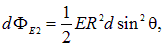
откуда находим полный поток через поверхность полусферы
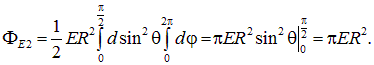
Мы получили, что поток через поверхность полусферы равен по абсолютной величине потоку через ее основание, так что с учетом знаков полный поток через замкнутую поверхность равен нулю
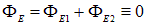 .
.
Теорема Гаусса для вектора 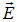 позволяет связать поток вектора напряженности через некоторую замкнутую поверхность с величиной зарядов, находящихся внутри этой поверхности. Рассмотрим для начала частный случай, а именно: определим поток вектора напряженности через произвольную воображаемую сферическую поверхность, в центре которой расположен точечный заряд.
позволяет связать поток вектора напряженности через некоторую замкнутую поверхность с величиной зарядов, находящихся внутри этой поверхности. Рассмотрим для начала частный случай, а именно: определим поток вектора напряженности через произвольную воображаемую сферическую поверхность, в центре которой расположен точечный заряд.
Линии напряженности векторного поля  точечного заряда представляют собой радиальные прямые, направленные от заряда, если он положителен, и к заряду, если он отрицателен (см. рис. 1.12). Поток вектора напряженности поля точечного заряда через сферическую поверхность радиусом r, центр которой совпадает с положением заряда и началом координат, равен
точечного заряда представляют собой радиальные прямые, направленные от заряда, если он положителен, и к заряду, если он отрицателен (см. рис. 1.12). Поток вектора напряженности поля точечного заряда через сферическую поверхность радиусом r, центр которой совпадает с положением заряда и началом координат, равен
|
|
(1.33) |
Здесь 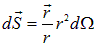 , где
, где 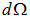 — элемент телесного угла, мы воспользовались значением полного телесного угла
— элемент телесного угла, мы воспользовались значением полного телесного угла
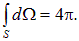
Можно показать, что поток вектора напряженности через любую замкнутую поверхность, охватывающую заряд q, не зависит от формы поверхности и равен 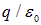 так же, как и для сферы. Физический смысл этого утверждения опять-таки заключается в том, что силовые линии начинаются и кончаются на зарядах. Поэтому непрерывная (без разрывов) деформация поверхности (показана на рис. 1.39-1 пунктиром) не изменит полного числа линий напряженности, выходящих наружу. Как следствие, поток через произвольную поверхность, охватывающую заряд, будет таким же, как и для сферы (см. рис. 1.39-1).
так же, как и для сферы. Физический смысл этого утверждения опять-таки заключается в том, что силовые линии начинаются и кончаются на зарядах. Поэтому непрерывная (без разрывов) деформация поверхности (показана на рис. 1.39-1 пунктиром) не изменит полного числа линий напряженности, выходящих наружу. Как следствие, поток через произвольную поверхность, охватывающую заряд, будет таким же, как и для сферы (см. рис. 1.39-1).
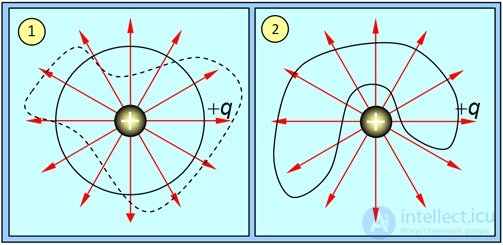
Рис. 1.39. Поток вектора Е через замкнутую поверхность:
1 — заряд находится внутри поверхности; 2 — заряд находится вне поверхности
Если же заряд находится вне ограниченного замкнутой поверхностью пространства, то линии напряженности пронизывают поверхность четное число раз (снаружи внутрь и изнутри наружу), в результате полный поток через поверхность, не охватывающую заряд, равен нулю (рис. 1.39-2).
Вывод теоремы Гаусса для точечного заряда, расположенного в произвольной точке, приведен в Дополнении 5.
Пусть теперь внутри и вне данной замкнутой поверхности имеется произвольное число точечных зарядов любого знака. В силу принципа суперпозиции суммарная напряженность поля будет представлять собой векторную сумму напряженностей полей каждого из зарядов
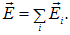
Полный поток напряженности поля через эту поверхность есть
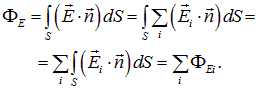
Используя , получаем соотношение, известное как теорема Гаусса для вектора 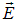 :
:
|
Поток вектора напряженности электрического поля через замкнутую |
продолжение следует...
Часть 1 1. Электрическое поле в вакууме
Часть 2 1.3. Электрическое поле. Напряженность и потенциал поля - 1. Электрическое
Часть 3 - 1. Электрическое поле в вакууме
Часть 4 1.4. Поток вектора. Теорема Остроградского-Гаусса для вектора - 1. Электрическое
Часть 5 1.5. Применение теоремы Гаусса для расчетов напряженности электрического поля -
Часть 6 Дополнения - 1. Электрическое поле в вакууме
Часть 7 Дополнение 2. Сила взаимодействия систем непрерывно распределенных зарядов - 1.
Комментарии
Оставить комментарий
Базовая физика
Термины: Базовая физика