Лекция
Это продолжение увлекательной статьи про электрическое поле в вакууме.
...
Интегрируя по 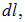 находим электрическое поле на оси кольца на расстоянии
находим электрическое поле на оси кольца на расстоянии 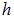 от его центра:
от его центра:
|
|
|
Отсюда находим искомую силу взаимодействия кольца с зарядом q:
|
|
|
Обсудим полученный результат. При больших расстояниях до кольца 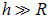 величиной радиуса кольца под знаком радикала можно пренебречь, и мы получаем приближенное выражение
величиной радиуса кольца под знаком радикала можно пренебречь, и мы получаем приближенное выражение
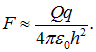
Это не удивительно, так как на больших расстояниях кольцо выглядит точечным зарядом 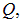 и сила взаимодействия дается обычным законом Кулона. На малых расстояниях ситуация резко меняется. Так, при помещении пробного заряда q в центр кольца
и сила взаимодействия дается обычным законом Кулона. На малых расстояниях ситуация резко меняется. Так, при помещении пробного заряда q в центр кольца 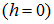 сила взаимодействия равна нулю. Это тоже не удивительно: в этом случае заряд q притягивается с равной силой всеми элементами кольца, и действие всех этих сил взаимно компенсируется.
сила взаимодействия равна нулю. Это тоже не удивительно: в этом случае заряд q притягивается с равной силой всеми элементами кольца, и действие всех этих сил взаимно компенсируется.
Поскольку при 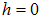 и при
и при 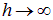 электрическое поле равно нулю, где-то при промежуточном значении
электрическое поле равно нулю, где-то при промежуточном значении 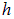 электрическое поле кольца максимально. Найдем эту точку, дифференцируя выражение для напряженности Е по расстоянию
электрическое поле кольца максимально. Найдем эту точку, дифференцируя выражение для напряженности Е по расстоянию 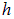
|
|
|
Приравнивая производную нулю, находим точку 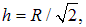 где поле максимально. Оно равно в этой точке
где поле максимально. Оно равно в этой точке
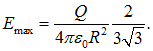
Пример 3. Две взаимно перпендикулярные бесконечно длинные нити, несущие равномерно распределенные заряды с линейными плотностями 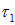 и
и 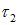 находятся на расстоянии а друг от друга (рис. 1.11). Как зависит сила взаимодействия между нитями от расстояния а?
находятся на расстоянии а друг от друга (рис. 1.11). Как зависит сила взаимодействия между нитями от расстояния а?
Решение. Сначала обсудим решение этой задачи методом анализа размерностей. Сила взаимодействия между нитями может зависеть от плотностей заряда на них, расстояния между нитями и электрической постоянной, то есть искомая формула имеет вид:
|
|
|
где 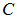 — безразмерная постоянная (число). Заметим, что вследствие симметричного расположения нитей плотности заряда на них могут входить только симметричным же образом, в одинаковых степенях. Размерности входящих сюда величин в СИ известны:
— безразмерная постоянная (число). Заметим, что вследствие симметричного расположения нитей плотности заряда на них могут входить только симметричным же образом, в одинаковых степенях. Размерности входящих сюда величин в СИ известны:
|
|
|
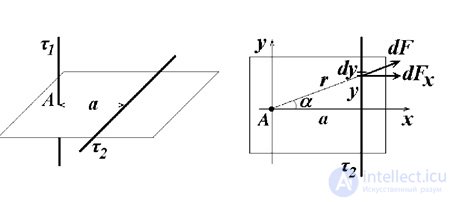
Рис. 1.11. Взаимодействие двух взаимно перпендикулярных бесконечно длинных нитей
По сравнению с механикой здесь появилась новая величина — размерность 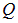 электрического заряда. Объединяя две предыдущие формулы, получаем уравнение для размерностей:
электрического заряда. Объединяя две предыдущие формулы, получаем уравнение для размерностей:
|
|
|
Приравнивая степени при М и Т в обеих частях этого уравнения, немедленно получаем 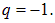 В левой части нет величины размерности заряда, откуда следует, что
В левой части нет величины размерности заряда, откуда следует, что 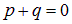 или
или 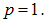 Наконец, приравнивая степени при размерности длины, получаем уравнение
Наконец, приравнивая степени при размерности длины, получаем уравнение 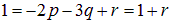 откуда следует, что
откуда следует, что 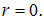 Окончательно имеем:
Окончательно имеем:
|
|
|
Таким образом, оказывается, что сила взаимодействия нитей не зависит от расстояния между ними. Напомним, что безразмерную постоянную С методом анализа размерностей определить невозможно. В сущности мы уже получили ответ на вопрос задачи, но приведем также и точное ее решение, которое позволит найти С. На рис. 1.11 справа показан вид сверху на плоскость, содержащую нить  точкой А отмечено сечение плоскостью чертежа нити
точкой А отмечено сечение плоскостью чертежа нити  . Напряженность электрического поля, создаваемого нитью
. Напряженность электрического поля, создаваемого нитью 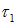 в точке, где находится элемент
в точке, где находится элемент 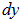 второй нити, равна
второй нити, равна
|
|
|
На элемент нити 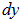 действует сила
действует сила
|
|
|
Нас, однако, интересует лишь компонента 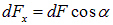 этой силы вдоль оси
этой силы вдоль оси 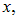 ибо продольная составляющая компенсируется точно такой же силой, действующей на симметричный элемент нити внизу. Выразим все расстояния через угол
ибо продольная составляющая компенсируется точно такой же силой, действующей на симметричный элемент нити внизу. Выразим все расстояния через угол 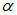 :
:
|
|
|
Получаем в итоге выражение для составляющей силы, действующей на элемент 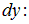
|
|
|
Интегрируя это выражение по углу 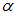 в пределах от
в пределах от 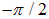 до
до 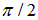 находим полную силу, действующую на нить:
находим полную силу, действующую на нить:
|
|
|
Мы снова убедились, что сила между нитями в данной задаче не зависит от расстояния 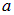 между ними. Кроме того, мы определили на сей раз безразмерную постоянную:
между ними. Кроме того, мы определили на сей раз безразмерную постоянную: 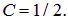
Вокруг всякого электрического заряда всегда существует электрическое поле.
|
Электрическое поле, созданное неподвижным зарядом (или системой неподвижных зарядов), называется электростатическим. |
Посредством электростатического поля осуществляется взаимодействие между зарядами. Само понятие поля оказалось весьма плодотворным и широко используется в современной физике. Появление поля означает, что что-то изменилось в окружающем нас пространстве. Математически поле описывается величиной, меняющейся от точки к точке. Например, можно рассмотреть поле скоростей в текущей жидкости. В каждой точке объема жидкости задан вектор скорости, который может меняться со временем (нестационарное течение), а может и быть постоянным (стационарное течение). Это пример векторного поля. К этому же типу полей относится и поле неподвижных электрических зарядов.
Напишем выражение для силы, действующей на точечный заряд  в результате его взаимодействия с системой точечных зарядов
в результате его взаимодействия с системой точечных зарядов 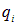 (соотношение Дополнения 1)
(соотношение Дополнения 1)
|
|
(1.6) |
Здесь 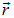 — радиус-вектор точки, в которой находится заряд
— радиус-вектор точки, в которой находится заряд  . Заряд
. Заряд  , на который, действует сила, в подобных ситуациях иногда называют «пробным» зарядом, выписан отдельным множителем. Выражение, стоящее в круглых скобках, определяется исключительно свойствами той системы зарядов, которая воздействует на заряд
, на который, действует сила, в подобных ситуациях иногда называют «пробным» зарядом, выписан отдельным множителем. Выражение, стоящее в круглых скобках, определяется исключительно свойствами той системы зарядов, которая воздействует на заряд  . Естественно, что это воздействие (сила) зависит от того, где он находится, соответственно, выражение в круглых скобках зависит от радиус-вектора
. Естественно, что это воздействие (сила) зависит от того, где он находится, соответственно, выражение в круглых скобках зависит от радиус-вектора 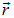 , определяющего местоположение заряда
, определяющего местоположение заряда  . Следуя изложенной выше идее об электростатическом поле существующем вокруг каждого заряда и, разумеется, системы зарядов, введем силовую характеристику этого поля, называемую напряженностью электрического поля.
. Следуя изложенной выше идее об электростатическом поле существующем вокруг каждого заряда и, разумеется, системы зарядов, введем силовую характеристику этого поля, называемую напряженностью электрического поля.
|
Напряженностью электрического поля называется вектор
|
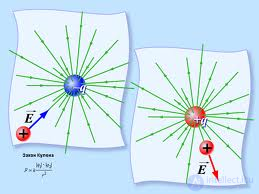
Рис. 1.12. Вектор напряженности электрического поля отрицательного и положительного точечного заряда
Из и определения напряженности вытекает, что напряженность поля произвольной системы покоящихся зарядов можно записать в виде
|
|
(1.8) |
Действительно, сила, с которой данная система зарядов действует на точечный заряд, равна векторной сумме сил, с которыми действует на него каждый из зарядов системы. Отсюда следует, что напряженность электрического поля системы зарядов определяется векторной суммой напряженностей полей, создаваемых отдельными зарядами системы. Имеет место так называемый принцип суперпозиции (независимого наложения) электрических полей
|
Напряженность поля, созданного системой неподвижных заряженных тел, равна векторной сумме напряженностей полей, создаваемых каждым телом в отдельности:
|
Принцип суперпозиции является одним из наиболее общих принципов современной физики. Подчеркнем, что напряженности поля складываются векторно.
На рис. 1.13 иллюстрируется принцип суперпозиции полей на примере поля, создаваемого двумя точечными зарядами.
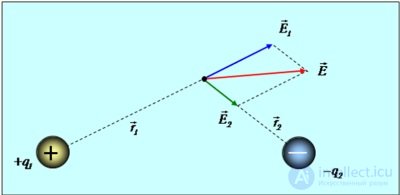
Рис. 1.13. Принцип суперпозиции электрических полей
Для одного заряда 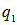 , находящегося в начале координат
, находящегося в начале координат 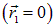 , для напряженности создаваемого им поля в точке с радиус-вектором
, для напряженности создаваемого им поля в точке с радиус-вектором 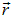 получаем (индекс 1 опущен):
получаем (индекс 1 опущен):
|
|
(1.9) |
Напряженность поля точечного заряда в различных точках пространства, в общем случае различна и по величине и по направлению (рис. 1.14). Поле точечного заряда — центральное поле, центр симметрии поля совпадает с точкой, в которой находится заряд.

Рис. 1.14. Векторы напряженности электрического поля заряда q в разных точках пространства
|
В СИ единицей измерения напряженности электрического поля является ньютон на кулон (Н/Кл), — то есть за единицу напряженности поля принята напряженность такого поля, в котором на заряд равный 1 Кл действует сила, равная 1 Н:
|
На практике чаще употребляют другое название этой единицы — «вольт на метр» (В/м) (про единицу «вольт» речь пойдет несколько позже).
Характерные значения напряженностей электрических полей, встречающихся в нашем мире, приведены на рис. 1.15.

Рис. 1.15. Характерные значения напряженностей электрических полей, встречающихся в природе
Обратим внимание на сходство закона Кулона с законом всемирного тяготения
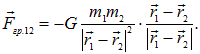
Роль зарядов играют массы, а гравитационная постоянная G аналогична коэффициенту 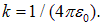 Знак минус соответствует тому, что гравитационное взаимодействие всегда является притяжением. Можно ввести и вектор напряженности гравитационного поля как отношение силы
Знак минус соответствует тому, что гравитационное взаимодействие всегда является притяжением. Можно ввести и вектор напряженности гравитационного поля как отношение силы 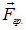 , например, к пробной массе
, например, к пробной массе 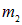 :
:
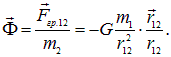
Если при этом 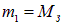 — масса Земли, а
— масса Земли, а 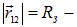 ее радиус, то
ее радиус, то 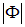 есть ни что иное, как хорошо знакомое ускорение свободного падения
есть ни что иное, как хорошо знакомое ускорение свободного падения 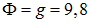 м/с2 (с точностью до весьма малой центробежной силы инерции, входящей в силу тяжести
м/с2 (с точностью до весьма малой центробежной силы инерции, входящей в силу тяжести 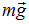 )
)
Пример 4. Среднее расстояние между электроном и протоном в атоме водорода равно r = 5,3·10–11 м (рис. 1.16). Найти силы электростатического 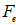 и гравитационного
и гравитационного 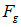 притяжения между ними и определить отношение этих сил.
притяжения между ними и определить отношение этих сил.

Рис. 1.16. Электрон и протон в атоме водорода
Решение. Из закона Кулона имеем
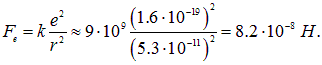
В свою очередь из закона всемирного тяготения следует
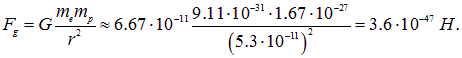
Отношение сил 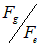 не зависит от расстояния между электроном и протоном и равно
не зависит от расстояния между электроном и протоном и равно
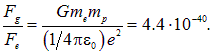
Этот расчет показывает, что в масштабах атомов и молекул силы гравитации столь меньше электростатических, что их можно не принимать во внимание.
Почему же в макромире, где мы обитаем, с законом гравитации мы знакомимся после первой же шишки на первых же шагах в детстве, а закон Кулона остается неизвестным многим из наших сограждан даже после окончания средней школы? Дело в том, что в макромире, как мы видели, положительные и отрицательные электрические заряды в телах скомпенсированы, так что в обычной жизни мы имеем дело с относительно небольшими избыточными зарядами. В то же время все тяготеющие массы имеют один и тот же знак, так что никакой компенсации масс не происходит, и силы гравитации проявляют себя в масштабах макромира в большей степени.
Электрическое поле можно задать, указав для каждой точки величину и направление вектора напряженности электрического поля  . Для наглядного изображения электрического поля используют силовые линии (или линии векторного поля
. Для наглядного изображения электрического поля используют силовые линии (или линии векторного поля  ).
).
|
Линией напряженности электрического поля (силовой линией) называется такая линия, касательная к которой в каждой ее точке совпадает по направлению с вектором напряженности электрического поля. |
На рис. 1.17 показана силовая линия электрического поля. Векторы напряженности электрического поля направлены по касательной к силовой линии.
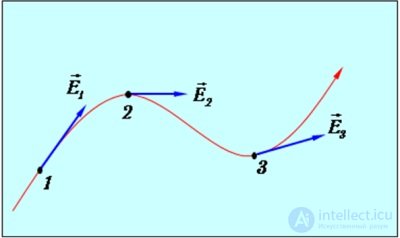
Рис. 1.17. Векторы напряженности электрического поля направлены по касательной к силовым линиям
Число линий, пронизывающих перпендикулярную к ним площадку единичной площади, пропорционально величине (модулю) напряженности электрического поля в данном месте. Другими словами силовые линии проводятся гуще там, где модуль напряженности поля больше. Таким образом, конфигурация силовых линий позволяет судить об изменении направления и величины вектора 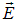 в пространстве. Картина линий векторного поля (не обязательно электрического или магнитного) весьма наглядный графический способ отображения его основных свойств.
в пространстве. Картина линий векторного поля (не обязательно электрического или магнитного) весьма наглядный графический способ отображения его основных свойств.
Отметим некоторые важные свойства силовых линий электростатического поля:
 была бы неоднозначной функцией координат точки);
была бы неоднозначной функцией координат точки);
Рис. 1.18. Силовые линии точечного заряда: 1 — q > 0; 2 — q < 0
В первом случае силовые линии начинаются на положительном точечном заряде и уходят в бесконечность, во втором случае силовые линии приходят из бесконечности и заканчиваются на отрицательном точечном заряде.
Силовые линии электрического поля, созданного двумя равными по модулю точечными одноименными зарядами, представлены на рис. 1.19.
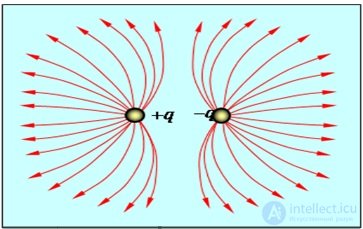
Рис. 1.19. Силовые линии электрического поля, образованного двумя равными положительными точечными зарядами
Картина силовых линий электрического поля, созданного двумя равными по модулю точечными разноименными зарядами, приведена на рис. 1.20.
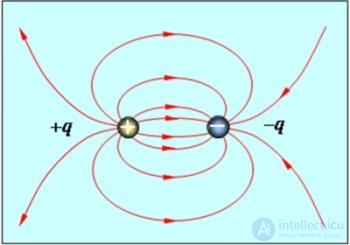
Рис. 1.20. Силовые линии электрического поля, образованного двумя разноименными равными по модулю точечными зарядами
Отметим, что, показанная (вместе со своим полем) на рис. 1.20 система двух равных по величине и противоположных по знаку зарядов, называется электрическим диполем.
Видео 1.5. Картина силовых линий поля точечного заряда, двух одинаковых точечных зарядов и диполя — двух разноименных точечных зарядов одной величины (бумажные «султаны»).
Видео 1.6. Картина силовых линий поля точечного заряда, диполя и цилиндрического конденсатора (манная крупа в касторовом масле).
|
Электрическое поле, напряженность которого одинакова по модулю и направлению во всех точках пространства, называется однородным электрическим полем. |
Густота и направление силовых линий по всему объему однородного электрического поля сохраняются неизменными. Такое поле графически изображается равноотстоящими друг от друга параллельными прямыми линиями.
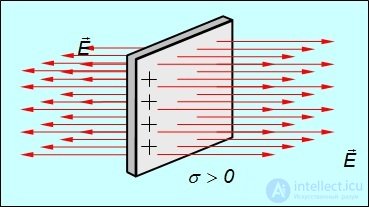
В дальнейшем будет показано, что бесконечная равномерно заряженная плоскость создает вокруг себя однородное электрическое поле. Линии напряженности поля направлены перпендикулярно заряженной плоскости и направлены от нее, если плоскость заряжена положительно, и к ней, если плоскость заряжена отрицательно (см. рис. 1.21).
|
Рис. 1.21. Электрическое поле равномерно положительно заряженной плоскости Силовые линии электрического поля можно исследовать экспериментально с помощью установки, изображенной на рис. 1.22. Электроды, присоединенные к источнику высокого напряжения, погружены в касторовое масло со взвесью мелких диэлектрических частиц. При подаче напряжения на электроды частицы выстраиваются цепочками вдоль силовых линий и показывают распределение поля в пространстве между электродами. Используя электроды различной формы, можно исследовать поле точечных зарядов одного и разных знаков, поле плоского и цилиндрического конденсаторов и др.
Рис. 1.22. Экспериментальное исследование силовых линий электростатического поля Поведение заряда в заданном электрическом поле описывается вторым законом Ньютона
|
продолжение следует...
Часть 1 1. Электрическое поле в вакууме
Часть 2 1.3. Электрическое поле. Напряженность и потенциал поля - 1. Электрическое
Часть 3 - 1. Электрическое поле в вакууме
Часть 4 1.4. Поток вектора. Теорема Остроградского-Гаусса для вектора - 1. Электрическое
Часть 5 1.5. Применение теоремы Гаусса для расчетов напряженности электрического поля -
Часть 6 Дополнения - 1. Электрическое поле в вакууме
Часть 7 Дополнение 2. Сила взаимодействия систем непрерывно распределенных зарядов - 1.
Комментарии
Оставить комментарий
Базовая физика
Термины: Базовая физика