Лекция
Это окончание невероятной информации про электрическое поле в вакууме.
...
src="/th/25/blogs/id8826/9236abe8b7a565be51d69fbf190dad50.png" data-auto-open loading="lazy" alt="1. Электрическое поле в вакууме" > и вторая: 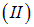
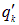 ,
, 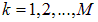 взаимодействуют между собой, то силу этого взаимодействия можно записать в виде следующей двойной суммы
взаимодействуют между собой, то силу этого взаимодействия можно записать в виде следующей двойной суммы
|
|
(1.62) |
Здесь, как и ранее, 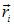 и
и 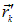 — радиус-векторы точек, в которых находятся соответствующие заряды.
— радиус-векторы точек, в которых находятся соответствующие заряды.
Формула , по крайней мере, в принципе, решает задачу вычисления сил кулоновского (электростатического) взаимодействия произвольных систем покоящихся точечных зарядов.
Под физически бесконечно малым участком понимается такой его участок, который, с одной стороны, настолько мал, что в условиях данной задачи, его можно считать материальной точкой, а, с другой стороны, он настолько велик, что дискретностью заряда (см. соотношение ) этого участка можно пренебречь.
Сделаем необходимое, на наш взгляд, дополнительное разъяснение по поводу слов «физически бесконечно малый» объем. Не следует рассматривать такой объем как результат формального, чисто математического предельного перехода к нулю. Физически бесконечно малый объем это объем, размер которого 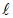 , с одной стороны, мал по сравнению с любой характерной длиной в рассматриваемой задаче
, с одной стороны, мал по сравнению с любой характерной длиной в рассматриваемой задаче 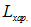 (напомним, что в разных задачах это весьма разные по величине длины) и его можно считать материальной точкой. С другой стороны, он макроскопически велик, то есть его размер
(напомним, что в разных задачах это весьма разные по величине длины) и его можно считать материальной точкой. С другой стороны, он макроскопически велик, то есть его размер 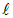 велик по сравнению со средним расстоянием между частицами
велик по сравнению со средним расстоянием между частицами 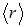 (атомами, молекулами, ионами, электронами и т. п.), составляющими вещество, так что этих частиц внутри физически бесконечно малого объема макроскопически много. Соответственно, тем, что это число меняется дискретно, можно пренебречь. Таким образом, линейный размер физически бесконечно малого объема должен удовлетворять следующему неравенству
(атомами, молекулами, ионами, электронами и т. п.), составляющими вещество, так что этих частиц внутри физически бесконечно малого объема макроскопически много. Соответственно, тем, что это число меняется дискретно, можно пренебречь. Таким образом, линейный размер физически бесконечно малого объема должен удовлетворять следующему неравенству
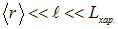
Отметим также, что величины вида 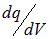 можно конечно рассматривать как производные, но наиболее просто, удобно и продуктивно рассматривать их как дроби: это отношение заряда
можно конечно рассматривать как производные, но наиболее просто, удобно и продуктивно рассматривать их как дроби: это отношение заряда 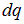 в объеме
в объеме 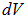 к величине этого объема.
к величине этого объема.
Два тела 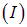 и
и 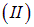 с объемами
с объемами 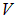 и
и  заряжены с плотностями
заряжены с плотностями 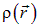 и
и 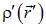 . В первом теле в окрестности точки с радиус-вектором
. В первом теле в окрестности точки с радиус-вектором 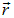 выделим физически бесконечно малый объем
выделим физически бесконечно малый объем 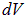 , внутри которого находится заряд
, внутри которого находится заряд  . Совершенно аналогично, во втором теле в окрестности точки с радиус-вектором
. Совершенно аналогично, во втором теле в окрестности точки с радиус-вектором 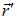 выделим физически бесконечно малый объем
выделим физически бесконечно малый объем 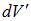 , внутри которого находится заряд
, внутри которого находится заряд 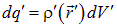 . Оба объема можно считать точечными зарядами, в соответствии с законом Кулона , напишем выражение для силы их взаимодействия:
. Оба объема можно считать точечными зарядами, в соответствии с законом Кулона , напишем выражение для силы их взаимодействия:
|
|
(1.63) |
Обратите внимание на то, что первое соотношение в отличается от соответствующего в только обозначениями. В последнем выражении в просто подставлены величины зарядов  и
и 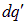 . Теперь, согласно принципу суперпозиции, необходимо просуммировать по всем парам точечных зарядов
. Теперь, согласно принципу суперпозиции, необходимо просуммировать по всем парам точечных зарядов 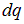 и
и 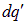 , из которых состоят первое и второе тела. Отличие от состоит в только том, что суммируются бесконечно малые силы взаимодействия пар бесконечно малых зарядов и их бесконечно много. Сумма бесконечно большого числа бесконечно малых величин есть интеграл. Поэтому в выражении, являющемся результатом такого суммирования, вместо сумм
, из которых состоят первое и второе тела. Отличие от состоит в только том, что суммируются бесконечно малые силы взаимодействия пар бесконечно малых зарядов и их бесконечно много. Сумма бесконечно большого числа бесконечно малых величин есть интеграл. Поэтому в выражении, являющемся результатом такого суммирования, вместо сумм
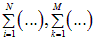
мы должны написать интегралы по объемам обоих тел 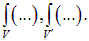 В результате получаем
В результате получаем
|
|
(1.64) |
Следовало бы успокоить читателя: нам не придется вычислять здесь шестикратные интегралы так же как и трехкратные, описывающие силу взаимодействия одного точечного заряда и протяженного тела
|
|
(1.65) |
с равномерно распределенным по нему зарядом с плотностью 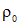 .
.
Рассмотрим примеры применения этих формул.
Пример 7. Проводящий диск радиусом 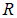 вращается с угловой скоростью
вращается с угловой скоростью 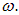 Учитывая, что ток в проводнике переносится электронами, определить разность потенциалов между осью диска и его периферией.
Учитывая, что ток в проводнике переносится электронами, определить разность потенциалов между осью диска и его периферией.
Решение. Получим сначала оценку результата с помощью анализа размерностей. В нашем распоряжении — заряд электрона 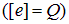 и его масса
и его масса 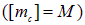 , угловая скорость
, угловая скорость 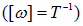 и радиус диска
и радиус диска 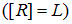 .
.
Искомая формула должна иметь вид:
|
|
|
Подставляя размерности, получаем:
|
|
|
откуда следуют уравнения (они же в данном случае — решение задачи):
|
|
|
|
|
|
Решим теперь задачу точно. Для того, чтобы электрон, находящийся внутри диска на расстоянии 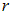 от оси, двигался по окружности, на него должна действовать центростремительная сила:
от оси, двигался по окружности, на него должна действовать центростремительная сила:
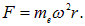
Эта сила обеспечивается перераспределением концентрации электронов в диске, создающей радиальное электрическое поле Е. Условие равновесия электрона:
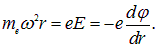
Проинтегрируем обе части этого уравнения:

где 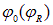 — потенциал в центре (на периферии) диска.
— потенциал в центре (на периферии) диска.
В результате получаем для разности потенциалов:
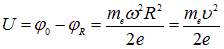
Где 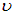 — линейная скорость точек на периферии диска. В принципе полученная формула может быть использована для определения отношения заряда электрона к его массе. Однако практически это крайне затруднительно. Приведем оценку. Заряд электрона
— линейная скорость точек на периферии диска. В принципе полученная формула может быть использована для определения отношения заряда электрона к его массе. Однако практически это крайне затруднительно. Приведем оценку. Заряд электрона 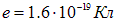 , его масса
, его масса 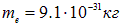 . Скорость на периферии диска примем равной 300 м/с. Разность потенциалов, возникающая между осью и периферией диска окажется при этом равной
. Скорость на периферии диска примем равной 300 м/с. Разность потенциалов, возникающая между осью и периферией диска окажется при этом равной 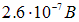 . Такое напряжение в движущейся системе измерить весьма сложно.
. Такое напряжение в движущейся системе измерить весьма сложно.
Пример 8. Сферическая капля воды, несущая электрический заряд 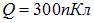 имеет на поверхности потенциал
имеет на поверхности потенциал 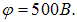 Каков радиус
Каков радиус 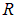 капли? Каким будет значение потенциала
капли? Каким будет значение потенциала 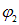 на поверхности новой сферической капли, образовавшейся при слиянии двух прежних? Какова зависимость потенциала на поверхности новой капли, образовавшейся при слиянии нескольких старых, от их числа n?
на поверхности новой сферической капли, образовавшейся при слиянии двух прежних? Какова зависимость потенциала на поверхности новой капли, образовавшейся при слиянии нескольких старых, от их числа n?
Решение. Потенциал на поверхности заряженной сферы (или шара — в данном случае это дает одинаковый результат) равен
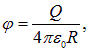
откуда находим радиус капли:
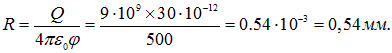
При слиянии n капель объемами 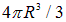 образуется новая капля радиусом
образуется новая капля радиусом 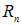 и увеличенным в
и увеличенным в 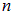 раз объемом:
раз объемом:
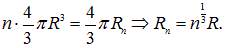
Новая капля будет нести также и увеличенный заряд: 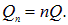 Отсюда находим для потенциала на ее поверхности:
Отсюда находим для потенциала на ее поверхности:
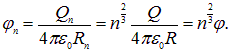
При слиянии двух капель получаем для потенциала
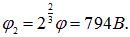
Рассмотрим общий вывод теоремы Гаусса. Он основан на прямом вычислении потока вектора напряженности поля точечного заряда через замкнутую поверхность 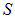 произвольной формы. Начало координат, как и ранее, поместим в ту точку пространства, в которой находится пока единственный заряд
произвольной формы. Начало координат, как и ранее, поместим в ту точку пространства, в которой находится пока единственный заряд 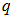 (см. рис. 1.59).
(см. рис. 1.59).
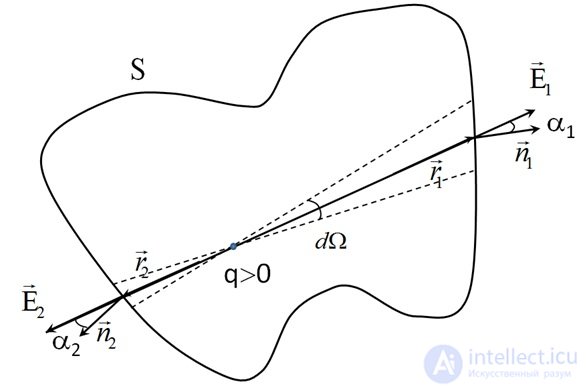
Рис. 1.59. Заряд внутри поверхности
Телесным углом 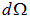 «вырежем» на противоположных сторонах поверхности
«вырежем» на противоположных сторонах поверхности 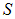 две площадки
две площадки 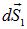 и
и 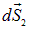 , внешние нормали к площадкам
, внешние нормали к площадкам 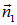 и
и 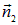 , напряженности поля
, напряженности поля 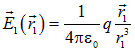 и
и 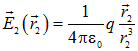 , соответственно. Вклады в поток от этих двух площадок
, соответственно. Вклады в поток от этих двух площадок
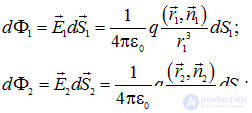
Скалярные произведения, входящие в выражения для потоков равны, очевидно: 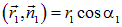 и
и  . Обе рассматриваемые площадки не лежат на сферических поверхностях, поэтому их площади в «|cos(α)|» раз больше тех, которые имели бы площадки, вырезанные тем же телесным углом, но на сферических поверхностях соответствующих радиусов (
. Обе рассматриваемые площадки не лежат на сферических поверхностях, поэтому их площади в «|cos(α)|» раз больше тех, которые имели бы площадки, вырезанные тем же телесным углом, но на сферических поверхностях соответствующих радиусов ( 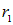 и
и 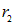 ), поэтому площади рассматриваемых нами площадок равны
), поэтому площади рассматриваемых нами площадок равны 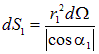 и
и 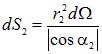 . В данном случае необходимо написать именно модуль косинуса, так как площадь не может быть отрицательной, а углы могут быть и тупыми, соответственно косинусы — отрицательными. Подставляя скалярные произведения и площади площадок в выражения для
. В данном случае необходимо написать именно модуль косинуса, так как площадь не может быть отрицательной, а углы могут быть и тупыми, соответственно косинусы — отрицательными. Подставляя скалярные произведения и площади площадок в выражения для 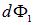 и
и 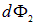 , получаем
, получаем
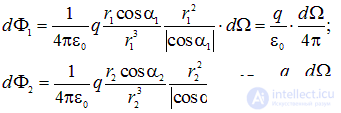
В написанных выше формулах учтено, что, в том случае, когда заряд 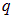 находится внутри поверхности
находится внутри поверхности 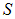 оба угла (
оба угла ( 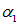 и
и 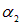 ) острые, оба косинуса положительны и в обоих случаях
) острые, оба косинуса положительны и в обоих случаях
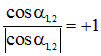
Выражения для 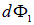 и
и 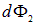 одинаковы, поэтому для любой площадки
одинаковы, поэтому для любой площадки 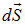 можно написать
можно написать 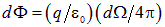 , интегрируя по всей поверхности, как и ранее, получаем
, интегрируя по всей поверхности, как и ранее, получаем
|
|
(1.66) |
Отметим, что равенство потоков 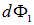 и
и 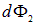 объясняется весьма просто: 1) площади площадок растут с ростом расстояния до той точки, в которой находится заряд, пропорционально квадрату этого расстояния, величина же напряженности поля убывает обратно пропорционально квадрату того же расстояния; 2) в силу центральности поля точечного заряда, в скалярное произведение
объясняется весьма просто: 1) площади площадок растут с ростом расстояния до той точки, в которой находится заряд, пропорционально квадрату этого расстояния, величина же напряженности поля убывает обратно пропорционально квадрату того же расстояния; 2) в силу центральности поля точечного заряда, в скалярное произведение 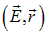 (в числителе) и в отношение площадей (в знаменателе) входит косинус (в первом случае) и модуль косинуса (во втором случае) одного и того же угла. Таким образом, равенство потоков
(в числителе) и в отношение площадей (в знаменателе) входит косинус (в первом случае) и модуль косинуса (во втором случае) одного и того же угла. Таким образом, равенство потоков 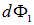 и
и 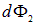 есть следствие свойств поля точечного заряда: его центральности и закона убывания
есть следствие свойств поля точечного заряда: его центральности и закона убывания 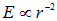 , то есть, в конечном счете, — закона Кулона.
, то есть, в конечном счете, — закона Кулона.
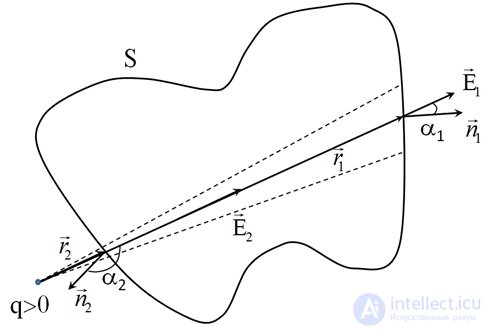
Рис. 1.60. Заряд вне поверхности
Если заряд 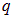 находится вне поверхности
находится вне поверхности 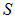 , то один из двух углов (см. рис. 1.60) тупой и, к примеру, как на рис. 1.59:
, то один из двух углов (см. рис. 1.60) тупой и, к примеру, как на рис. 1.59:
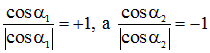 ,
,
тогда сумма
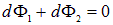 .
.
В этом случае, интегрируя по всей поверхности, имеем
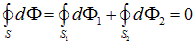
В последнем выражении 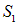 — «дальняя» от заряда
— «дальняя» от заряда 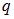 часть поверхности, на которой
часть поверхности, на которой 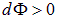 , а
, а 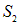 — «ближняя» к заряду
— «ближняя» к заряду 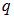 часть, на которой
часть, на которой 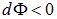 . Объединяя оба результата, и для поверхности произвольной формы получаем:
. Объединяя оба результата, и для поверхности произвольной формы получаем:
|
|
(1.67) |
Вывод теоремы Гаусса в общем виде можно найти также, например, в учебнике И.Е. Тамм, «Основы теории электричества», Москва, Наука, 1989, стр. 18.
Получим весьма полезную на практике формулу вычисления градиента скалярной функции обладающей сферической
|
|
(1.68) |
или цилиндрической
|
|
(1.69) |
симметрией. Такого рода функции появляются всякий раз, когда мы имеем дело с полями сферической или осевой симметрии с тем отличием, что в первом случае 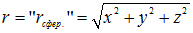 — расстояние до центра симметрии поля, с которым совмещено начало координат, а во втором
— расстояние до центра симметрии поля, с которым совмещено начало координат, а во втором 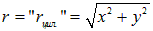 — расстояние до оси симметрии поля, вдоль которой направлена ось
— расстояние до оси симметрии поля, вдоль которой направлена ось 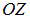 системы координат. Оба эти случая можно рассмотреть единообразно.
системы координат. Оба эти случая можно рассмотреть единообразно.
Для начала вычислим 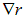 .
.
Выполняя дифференцирование, получаем
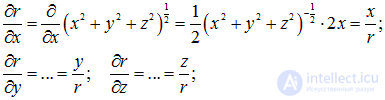
Теперь умножим каждую частную производную на орт соответствующей оси и сложим результаты
|
|
(1.70) |
Вычислим теперь градиент произвольной скалярной функции, зависящей только от модуля радиус-вектора 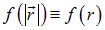 . В обоих случаях
. В обоих случаях 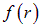 есть сложная функция координат
есть сложная функция координат 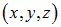 точки: функция
точки: функция 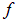 зависит от них не непосредственно и независимо, а через посредство внутренней функции
зависит от них не непосредственно и независимо, а через посредство внутренней функции 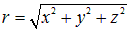 . Согласно правилу дифференцирования сложных функций
. Согласно правилу дифференцирования сложных функций
|
|
(1.71) |
Сравнение с показывает, что есть просто частный случай для 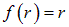 , когда
, когда 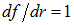 .
.
Таким образом, общая формула для градиента скалярной функции, зависящей только от модуля радиус-вектора, имеет вид:
|
|
(1.72) |
В частном случае потенциала поля 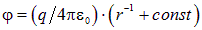 точечного заряда, находящегося в начале координат, как и должно быть, получаем
точечного заряда, находящегося в начале координат, как и должно быть, получаем
|
|
(1.73) |
Предлагаем самостоятельно вывести следующие полезные соотношения:
|
|
(1.74) |
В в операторе 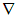 в первом соотношении дифференцирование производится по координатам
в первом соотношении дифференцирование производится по координатам 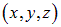 точки с радиус-вектором
точки с радиус-вектором 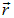 , а в операторе
, а в операторе 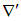 во втором соотношении — по координатам точки
во втором соотношении — по координатам точки 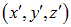 с радиус-вектором
с радиус-вектором 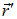 . Для упрощения вывода рекомендуется сделать замену
. Для упрощения вывода рекомендуется сделать замену 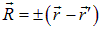 .
.
Исследование, описанное в статье про электрическое поле в вакууме, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое электрическое поле в вакууме и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Переменный электрический ток. Электромагнитное поле
Часть 1 1. Электрическое поле в вакууме
Часть 2 1.3. Электрическое поле. Напряженность и потенциал поля - 1. Электрическое
Часть 3 - 1. Электрическое поле в вакууме
Часть 4 1.4. Поток вектора. Теорема Остроградского-Гаусса для вектора - 1. Электрическое
Часть 5 1.5. Применение теоремы Гаусса для расчетов напряженности электрического поля -
Часть 6 Дополнения - 1. Электрическое поле в вакууме
Часть 7 Дополнение 2. Сила взаимодействия систем непрерывно распределенных зарядов - 1.
Комментарии
Оставить комментарий
Базовая физика
Термины: Базовая физика