Лекция
Привет, сегодня поговорим про дискретное преобразование фурье, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое дискретное преобразование фурье, дпф , настоятельно рекомендую прочитать все из категории Цифровая обработка сигналов.
дискретное преобразование фурье (в англоязычной литературе DFT, Discrete Fourier Transform) — это одно из преобразований Фурье, широко применяемых в алгоритмах цифровой обработки сигналов (его модификации применяются в сжатии звука в MP3, сжатии изображений в JPEG и др.), а также в других областях, связанных с анализом частот в дискретном (к примеру, оцифрованном аналоговом) сигнале. Дискретное преобразование Фурье требует в качестве входа дискретную функцию. Такие функции часто создаются путем дискретизации (выборки значений из непрерывных функций). Дискретные преобразования Фурье помогают решать дифференциальные уравнения в частных производных и выполнять такие операции, как свертки. Дискретные преобразования Фурье также активно используются в статистике, при анализе временных рядов. Существуют многомерные дискретные преобразования Фурье.
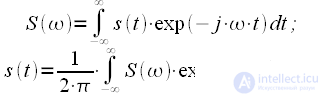 |
(1) |
 – спектр сигнала
– спектр сигнала 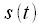 (в общем случае и сигнал и спектр — комплексные).
(в общем случае и сигнал и спектр — комплексные).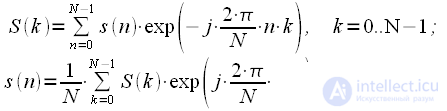 |
(2) |
 отсчетам сигнала
отсчетам сигнала 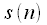 ,
, 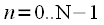 , в общем случае комплексного,
, в общем случае комплексного,  отсчетов спектра
отсчетов спектра 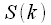 ,
, 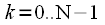 .
.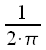 , в случае ОДПФ –
, в случае ОДПФ – 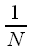 . Можно отметить, что в случае непрерывного преобразования нормировочный коэффициент
. Можно отметить, что в случае непрерывного преобразования нормировочный коэффициент 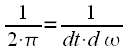 призван корректно отображать масштабирование сигнала во времени в частотную область и наоборот. Другими словами, если последовательно рассчитать спектр некоторого сигнала, а после взять обратное преобразование Фурье, то результат обратного преобразования должен полностью совпадать с исходным сигналом. Нормировочный коэффициент
призван корректно отображать масштабирование сигнала во времени в частотную область и наоборот. Другими словами, если последовательно рассчитать спектр некоторого сигнала, а после взять обратное преобразование Фурье, то результат обратного преобразования должен полностью совпадать с исходным сигналом. Нормировочный коэффициент 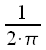 уменьшает амплитуду сигнала на выходе обратного преобразования для того чтобы она совпадала с амплитудой исходного сигнала.
уменьшает амплитуду сигнала на выходе обратного преобразования для того чтобы она совпадала с амплитудой исходного сигнала.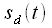 , как результат умножения непрерывного сигнала
, как результат умножения непрерывного сигнала 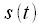 на решетчатую функцию
на решетчатую функцию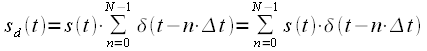 , , |
(3) |
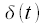 – дельта-функция,
– дельта-функция,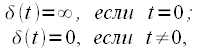 |
(4) |
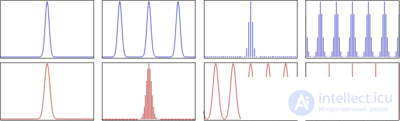
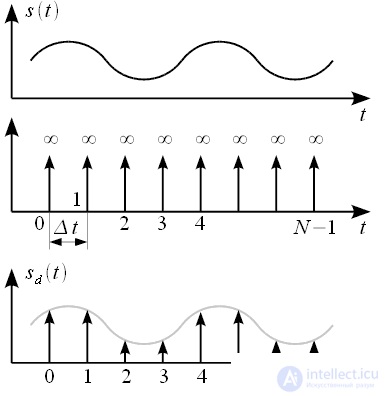
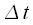 – интервал дискретизации. Графически процесс дискретизации можно представить как это показано на рисунке 1.
– интервал дискретизации. Графически процесс дискретизации можно представить как это показано на рисунке 1.
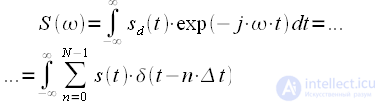 |
(5) |
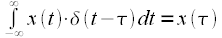 . . |
(6) |
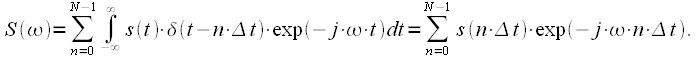 |
(7) |
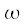 меняется на всей числовой оси. Однако можно заметить что комплексные экспоненты под знаком суммы в выражении (7) являются периодическими функциями с периодом:
меняется на всей числовой оси. Однако можно заметить что комплексные экспоненты под знаком суммы в выражении (7) являются периодическими функциями с периодом: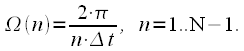 |
(8) |
 исключено из выражения (8), так как при
исключено из выражения (8), так как при  комплексная экспонента равна единице для всех частот. Таким образом максимальный период повторения спектра
комплексная экспонента равна единице для всех частот. Таким образом максимальный период повторения спектра  будет при
будет при 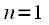 и равен
и равен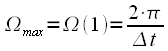 . . |
(9) |
 при
при 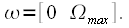
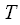 , тогда его спектр будет содержать дискретные гармоники кратные
, тогда его спектр будет содержать дискретные гармоники кратные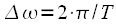 . Графически процесс повторения сигнала во времени представлен на рисунке 2.
. Графически процесс повторения сигнала во времени представлен на рисунке 2.

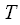 .
.
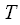 , однако необходимо чтобы период повторения был более или равен длительности сигнала, т.е.
, однако необходимо чтобы период повторения был более или равен длительности сигнала, т.е. 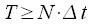 . При этом минимальный период повторения сигнала
. При этом минимальный период повторения сигнала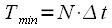 . . |
(10) |
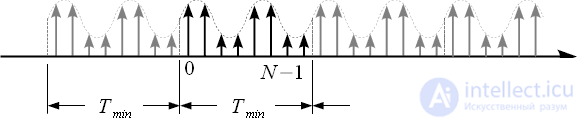
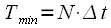 представлен на рисунке 3.
представлен на рисунке 3.
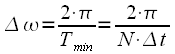 |
(11) |
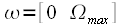 получим
получим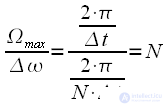 |
(12) |
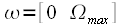 с шагом
с шагом 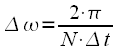 и получим тем самым
и получим тем самым  отсчетов спектра. Учтем вышесказанное в выражении (7), получим:
отсчетов спектра. Учтем вышесказанное в выражении (7), получим: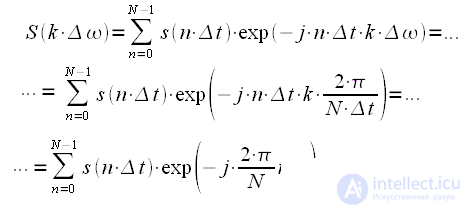 |
(13) |
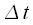 и по частоте
и по частоте  , то получим окончательное выражение для ДПФ:
, то получим окончательное выражение для ДПФ: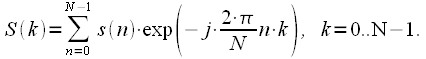 |
(14) |
 отсчетам дискретного сигнала
отсчетам дискретного сигнала  отсчетов дискретного спектра, при этом предполагается, что и сигнал и спектр являются периодическими и анализируются на одном периоде.
отсчетов дискретного спектра, при этом предполагается, что и сигнал и спектр являются периодическими и анализируются на одном периоде.
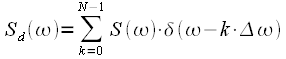 , , |
(15) |
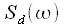 - дискретные отсчеты спектра на одном периоде повторения
- дискретные отсчеты спектра на одном периоде повторения 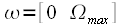 . Подставим в выражение для обратного преобразования Фурье (1):
. Подставим в выражение для обратного преобразования Фурье (1):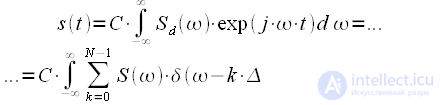 |
(16) |
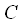 – коэффициент пропорциональности, задача которого обеспечить равенство по амплитуде исходного дискретного сигнала и результата ОДПФ коэффициент пропорциональности учитывает коэффициент
– коэффициент пропорциональности, задача которого обеспечить равенство по амплитуде исходного дискретного сигнала и результата ОДПФ коэффициент пропорциональности учитывает коэффициент 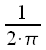 . Поменяем местами операции суммирования и интегрирования и учтем фильтрующее свойство дельта-функции получим:
. Поменяем местами операции суммирования и интегрирования и учтем фильтрующее свойство дельта-функции получим: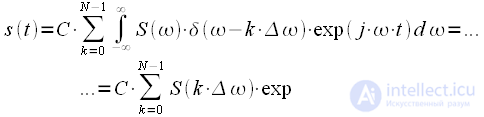 |
(17) |
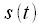 через интервал
через интервал 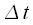 , тогда (17) можно записать:
, тогда (17) можно записать: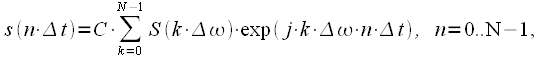 |
(18) |
 |
(19) |
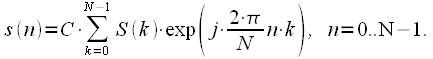 |
(20) |
 , необходимо в выражение для ОДПФ (20) подставить выражение для расчета спектра при помощи ДПФ (14), получим:
, необходимо в выражение для ОДПФ (20) подставить выражение для расчета спектра при помощи ДПФ (14), получим: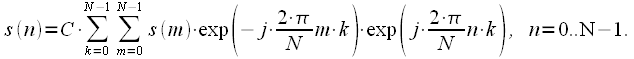 |
(21) |
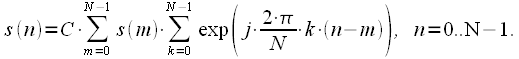 |
(22) |
 получаем:
получаем: |
(23) |
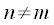 . Пусть
. Пусть 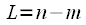 , тогда получаем:
, тогда получаем: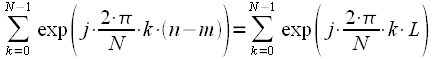 . . |
(24) |
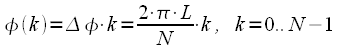 , , |
(25) |
 и они повернуты относительно друг друга на одинаковые углы. Поскольку все векторы выходят из одной точки (из 0 комплексной плоскости) и повернуты относительно друг друга на одинаковые углы, то их сумма равна нулю. Это иллюстрируется наглядно для
и они повернуты относительно друг друга на одинаковые углы. Поскольку все векторы выходят из одной точки (из 0 комплексной плоскости) и повернуты относительно друг друга на одинаковые углы, то их сумма равна нулю. Это иллюстрируется наглядно для 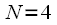 на рисунке 4.
на рисунке 4.

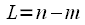 ,
, 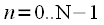 ,
, 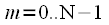 ,
, 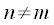 , суммы комплексных экспонент (24) действительно равны нулю. Тогда в выражении (22) от суммы по
, суммы комплексных экспонент (24) действительно равны нулю. Тогда в выражении (22) от суммы по 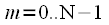 , останется только слагаемое при
, останется только слагаемое при  . Тогда можно записать (22):
. Тогда можно записать (22):
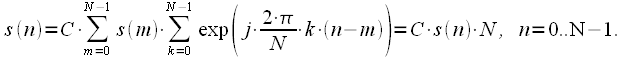 |
(26) |
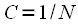 . Таким образом выражение для ОДПФ можно окончательно записать:
. Таким образом выражение для ОДПФ можно окончательно записать: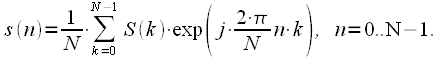 |
(27) |
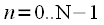 и спектральных
и спектральных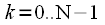 отсчетов без учета частоты дискретизации. Это позволяет использовать выражения для ДПФ и ОДПФ при любой частоте дискретизации не меняя вычислительную программу. Это несомненный плюс ДПФ, при этом если необходимо привязать индексы к частоте дискретизации (к реальной оси частот), то нужно вспомнить, что частотный спектр дискретизировался с шагом
отсчетов без учета частоты дискретизации. Это позволяет использовать выражения для ДПФ и ОДПФ при любой частоте дискретизации не меняя вычислительную программу. Это несомненный плюс ДПФ, при этом если необходимо привязать индексы к частоте дискретизации (к реальной оси частот), то нужно вспомнить, что частотный спектр дискретизировался с шагом 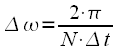 рад/c, или
рад/c, или 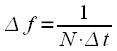 Гц, где
Гц, где 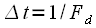 ,
, 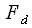 – частота дискретизации в Гц. Таким образом, если известна частота дискретизации, то
– частота дискретизации в Гц. Таким образом, если известна частота дискретизации, то  - ый спектральный отсчет соответствует частоте
- ый спектральный отсчет соответствует частоте  рад/c или
рад/c или 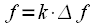 Гц. Например при частоте дискретизации
Гц. Например при частоте дискретизации  кГц, при
кГц, при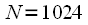 ,
, 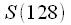 спектральный отсчет соответствует частоте
спектральный отсчет соответствует частоте 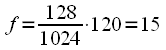 кГц.
кГц.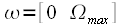 . При этом в силу периодичности спектра дискретного сигнала отсчеты
. При этом в силу периодичности спектра дискретного сигнала отсчеты 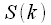 при
при  соответствуют как частотам
соответствуют как частотам 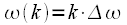 , так и частотам
, так и частотам 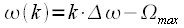 , где
, где 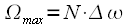 , то есть
, то есть 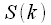 при
при соответствуют отрицательным частотам
соответствуют отрицательным частотам 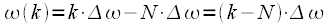 , т.е. физически при
, т.е. физически при вторая половина спектра это частоты от -
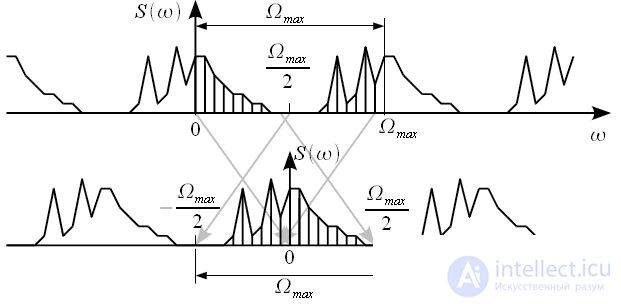
вторая половина спектра это частоты от -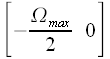 . Это наглядно иллюстрируется рисунком 5. Для того, чтобы из спектра в интервале частот
. Это наглядно иллюстрируется рисунком 5. Для того, чтобы из спектра в интервале частот 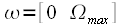 , рассчитанного при помощи дискретного преобразования Фурье, получить спектр сигнала в интервале
, рассчитанного при помощи дискретного преобразования Фурье, получить спектр сигнала в интервале  необходимо поменять местами две половины спектральных отсчетов (смотри рисунок 5).
необходимо поменять местами две половины спектральных отсчетов (смотри рисунок 5).
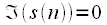 для
для 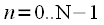 , тогда
, тогда
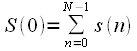 |
(28) |
 - четное, тогда
- четное, тогда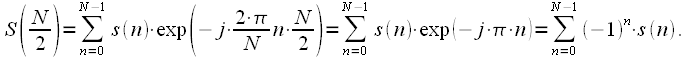 |
(29) |
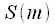 ,
, 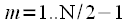 и
и 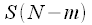 :
: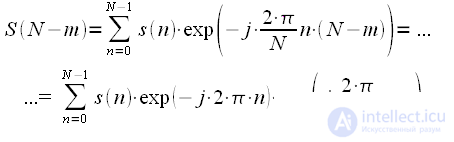 |
(30) |
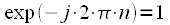 , тогда можно сделать вывод:
, тогда можно сделать вывод: 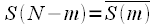 ,
, 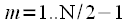 , то есть вторая половина спектральных отсчетов комплексно сопряжена с первой. На рисунке 6 представлен вид действительной и мнимой части комплексного спектра действительного сигнала при четном
, то есть вторая половина спектральных отсчетов комплексно сопряжена с первой. На рисунке 6 представлен вид действительной и мнимой части комплексного спектра действительного сигнала при четном  . Красным отмечены чисто вещественные
. Красным отмечены чисто вещественные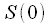 и
и  .
.
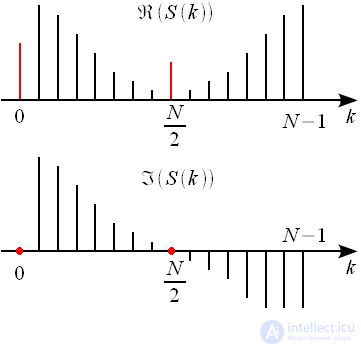
Дискретное преобразование Фурье вектора может быть интерпретировано как вычисление значений многочлена
в корнях из единицы
,
,
, …,
.
Значения многочлена -й степени в
точках однозначно определяют сам многочлен. В то же время, если
и
, то
, потому по значениям многочленов
и
можно также определить значения в тех же точках многочлена
и восстановить его обратным дискретным преобразованием Фурье.
Так как любое число представимо в виде многочлена от основания системы счисления , умножение двух чисел может быть в свою очередь сведено к умножению двух многочленов и нормализации результата.
ДПФ широко используется в большом количестве полей; мы только набросаем несколько примеров ниже (см. также ссылки в конце). Все приложения ДПФ в решающей степени зависят от наличия быстрого алгоритма для вычисления дискретных преобразований Фурье и их обратных, быстрого преобразования Фурье .
Когда ДПФ используется для спектрального анализа сигнала , Последовательность обычно представляет собой конечный набор равномерно распределенных временных отсчетов некоторого сигнала.
, где
представляет время . Переход от непрерывного времени к образцам ( с дискретным временем) меняет лежащий в основе преобразования Фурье из
в дискретное преобразование Фурье (DTFT), которое обычно влечет за собой тип искажения, называемый наложением спектров . Выбор подходящей частоты дискретизации (см. Частота Найквиста ) является ключом к минимизации этого искажения. Точно так же преобразование очень длинной (или бесконечной) последовательности в управляемый размер влечет за собой тип искажения, называемый утечкой , который проявляется в виде потери деталей (или разрешения) в DTFT. Выбор подходящей длины подпоследовательности является основным ключом к минимизации этого эффекта. Когда доступных данных (и времени на их обработку) больше, чем количество, необходимое для достижения желаемого частотного разрешения, стандартным методом является выполнение нескольких ДПФ, например, для создания спектрограммы.. Если желаемый результат представляет собой спектр мощности, а в данных присутствует шум или случайность, усреднение составляющих амплитуды нескольких ДПФ является полезной процедурой для уменьшения дисперсии спектра (также называемой периодограммой в этом контексте); два примера таких методов являются метод Велч и метод Бартлетта ; Общий предмет оценки спектра мощности зашумленного сигнала называется спектральной оценкой .
Последним источником искажения (или, возможно, иллюзии ) является само ДПФ, потому что это всего лишь дискретная выборка ДВПФ, которая является функцией непрерывной частотной области. Это можно смягчить, увеличив разрешение ДПФ. Эта процедура проиллюстрирована в § Выборка ДВПФ .
Банки фильтров БПФ и Выборка ДВПФ .
При обработке сигналов набор фильтров (или набор фильтров ) представляет собой массив полосовых фильтров, которые разделяют входной сигнал на несколько компонентов, каждый из которых несет одну частотную поддиапазону исходного сигнала. Одним из применений банка фильтров является графический эквалайзер , который может по-разному ослаблять компоненты и рекомбинировать их в модифицированную версию исходного сигнала. Процесс декомпозиции, выполняемый банком фильтров, называется анализом.(имеется в виду анализ сигнала с точки зрения его компонентов в каждом поддиапазоне); результат анализа упоминается как сигнал поддиапазона с таким количеством поддиапазонов, сколько имеется фильтров в банке фильтров. Процесс восстановления называется синтезом , что означает восстановление полного сигнала, полученного в результате процесса фильтрации.
В цифровой обработке сигналов термин « банк фильтров» также обычно применяется к группе приемников. Разница в том, что приемники также преобразуют поддиапазоны с понижением частоты до низкой центральной частоты, которая может быть повторно дискретизирована с пониженной скоростью. Тот же результат иногда может быть достигнут за счет недостаточной дискретизации поддиапазонов полосы пропускания.
Еще одно применение банков фильтров - это сжатие сигналов, когда одни частоты важнее других. После разложения важные частоты могут быть закодированы с высоким разрешением. Небольшие различия на этих частотах значительны, и необходимо использовать схему кодирования , которая сохраняет эти различия. С другой стороны, менее важные частоты не обязательно должны быть точными. Можно использовать более грубую схему кодирования, даже если некоторые из более мелких (но менее важных) деталей будут потеряны при кодировании.
Вокодера использует банк фильтров для определения информации об амплитуде из поддиапазонов сигнала модулятора (например, голос) и использует их , чтобы управлять амплитудой поддиапазонов сигнала несущей (например, выход гитары или синтезатора), таким образом накладывая динамические характеристики модулятора на несущую.
Область цифровой обработки сигналов в значительной степени зависит от операций в частотной области (т. Е. От преобразования Фурье). Например, несколько методов сжатия изображений и звука с потерями используют дискретное преобразование Фурье: сигнал разрезается на короткие сегменты, каждый преобразуется, а затем коэффициенты Фурье высоких частот, которые считаются незаметными, отбрасываются. Декомпрессор вычисляет обратное преобразование на основе этого уменьшенного числа коэффициентов Фурье. (Приложения сжатия часто используют специализированную форму ДПФ, дискретное косинусное преобразование или иногда модифицированное дискретное косинусное преобразование .) Однако некоторые относительно недавние алгоритмы сжатия используют вейвлет-преобразования., которые дают более равномерный компромисс между временной и частотной областями, чем полученный путем разделения данных на сегменты и преобразования каждого сегмента. В случае JPEG2000 это позволяет избежать ложных характеристик изображения, которые появляются, когда изображения сильно сжаты с исходным JPEG .
Дискретные преобразования Фурье часто используются для решения уравнений в частных производных , где снова ДПФ используется в качестве приближения для ряда Фурье (который восстанавливается в пределе бесконечного N ). Преимущество этого подхода в том, что он расширяет сигнал в комплексные экспоненты., которые являются собственными функциями дифференцирования:
. Таким образом, в представлении Фурье дифференцирование выполняется просто - мы просто умножаем на
. (Однако выбор
не уникален из-за алиасинга; чтобы метод был сходимым, следует использовать выбор, аналогичный тому, что был в предыдущем разделе тригонометрической интерполяции .) Линейное дифференциальное уравнение с постоянными коэффициентами преобразуется в легко решаемое алгебраическое уравнение . Затем используется обратное ДПФ, чтобы преобразовать результат обратно в обычное пространственное представление. Такой подход называется спектральным методом .
Предположим, мы хотим вычислить полиномиальное произведение c ( x ) = a ( x ) · b ( x ). Обычное выражение произведения для коэффициентов c включает линейную (ациклическую) свертку, при которой индексы не «зацикливаются». Это можно переписать как циклическую свертку, взяв сначала векторы коэффициентов для a ( x ) и b ( x ) с постоянным членом, а затем добавив нули так, чтобы результирующие векторы коэффициентов a и b имели размерность d > deg ( a ( x)) + deg ( b ( x )) . Потом,
Где c - вектор коэффициентов для c ( x ), а оператор свертки определяется так
Но свертка становится умножением под ДПФ:
Здесь векторное произведение берется поэлементно. Таким образом, коэффициенты полинома произведения c ( x ) - это просто члены 0, ..., deg ( a ( x )) + deg ( b ( x )) вектора коэффициентов
С быстрым преобразованием Фурье результирующий алгоритм требует O ( N log N ) арифметических операций. Из-за своей простоты и скорости алгоритм БПФ Кули-Тьюки , который ограничен составными размерами, часто выбирается для операции преобразования. В этом случае d следует выбирать как наименьшее целое число , большее суммы степеней входного полинома, которое может быть разложено на малые простые множители (например, 2, 3 и 5, в зависимости от реализации БПФ).
Самые быстрые известные алгоритмы умножения очень больших целых чисел используют метод полиномиального умножения, описанный выше. Целые числа можно трактовать как значение многочлена, вычисляемого специально по числовой базе, с коэффициентами многочлена, соответствующими цифрам в этой базе (например,). После полиномиального умножения, относительно несложный этап распространения переноса завершает умножение .
Когда данные свертываются с помощью функции с широкой поддержкой, такой как понижающая дискретизация с большим коэффициентом дискретизации, из-за теоремы свертки и алгоритма БПФ может быть быстрее преобразовать их, умножить поточечно на преобразование фильтра и затем отменить преобразовать его. В качестве альтернативы хороший фильтр получается путем простого усечения преобразованных данных и повторного преобразования сокращенного набора данных.
Существуют различные альтернативы ДПФ для различных приложений, среди которых выделяются вейвлеты . Аналогом ДПФ является дискретное вейвлет-преобразование (ДВП). С точки зрения частотно-временного анализа , ключевым ограничением преобразования Фурье является то, что оно не включает информацию о местоположении , а только частотную информацию, и, таким образом, затрудняет представление переходных процессов. Поскольку вейвлеты имеют местоположение, а также частоту, они лучше могут представлять местоположение за счет большей сложности с представлением частоты. Подробнее см. Сравнение дискретного вейвлет -преобразования с дискретным преобразованием Фурье .
Надеюсь, эта статья про дискретное преобразование фурье, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое дискретное преобразование фурье, дпф и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровая обработка сигналов
Комментарии
Оставить комментарий
Цифровая обработка сигналов
Термины: Цифровая обработка сигналов