Лекция
Привет, сегодня поговорим про спектральный анализ на ограниченном интервале времени оконные функции, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое спектральный анализ на ограниченном интервале времени оконные функции , настоятельно рекомендую прочитать все из категории Цифровая обработка сигналов.
Пусть имеется сигнал 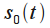 который бесконечен во времени. В простейшем случае мы можем задать этот сигнал как гармоническое колебание с частотой
который бесконечен во времени. В простейшем случае мы можем задать этот сигнал как гармоническое колебание с частотой 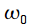 . Преобразование Фурье этого сигнала будет представлять собой дельта-импульс на частоте сигнала, т.е.
. Преобразование Фурье этого сигнала будет представлять собой дельта-импульс на частоте сигнала, т.е.  . Исходный сигнал и его спектр показаны на рисунке синим цветом. На практике мы не можем произвести расчет спектра путем численного интегрирования по всей оси времени (разумеется за исключением когда мы можем получить аналитическое выражение для спектра сигнала, как в приведенном примере), поэтому мы зафиксируем интервал времени
. Исходный сигнал и его спектр показаны на рисунке синим цветом. На практике мы не можем произвести расчет спектра путем численного интегрирования по всей оси времени (разумеется за исключением когда мы можем получить аналитическое выражение для спектра сигнала, как в приведенном примере), поэтому мы зафиксируем интервал времени  на котором будем рассчитывать спектр сигнала. Таким образом мы получим сигнал
на котором будем рассчитывать спектр сигнала. Таким образом мы получим сигнал 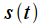 , который совпадает с исходным на интервале времени
, который совпадает с исходным на интервале времени  , но вне интервала наблюдения считаем
, но вне интервала наблюдения считаем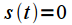 . Математически,
. Математически, 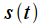 можно представить как произведение исходного бесконечного сигнала
можно представить как произведение исходного бесконечного сигнала 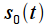 и прямоугольного импульса
и прямоугольного импульса 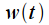 длительностью
длительностью ,
, 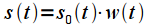 . Спектр же сигнала
. Спектр же сигнала 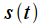 , согласно свойствам преобразования Фурье будет равен свертке спектров исходного сигнала и спектра
, согласно свойствам преобразования Фурье будет равен свертке спектров исходного сигнала и спектра 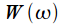 прямоугольного импульса
прямоугольного импульса 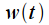 :
:
 |
(1) |
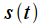 и его спектр
и его спектр 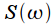 показаны на рисунке 1 красным цветом.
показаны на рисунке 1 красным цветом.
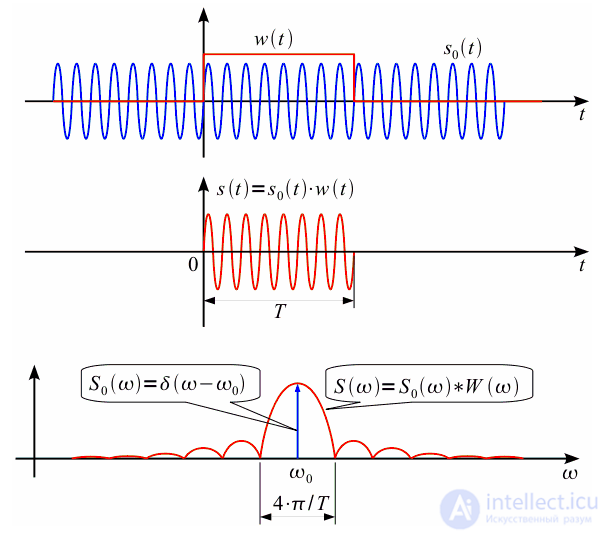
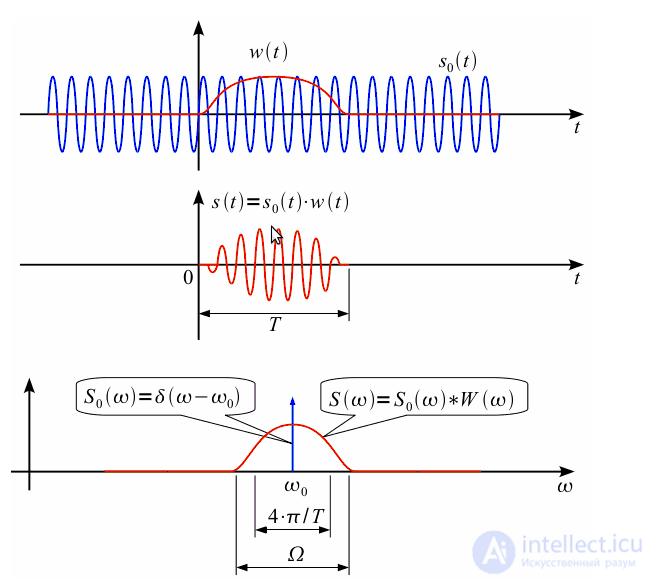
 превратился в функцию типа
превратился в функцию типа  , (спектр прямоугольного импульса функции
, (спектр прямоугольного импульса функции 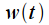 ) причем ширина лепестка зависит от длительности интервала анализа, как это наглядно показано на рисунке 2.
) причем ширина лепестка зависит от длительности интервала анализа, как это наглядно показано на рисунке 2.
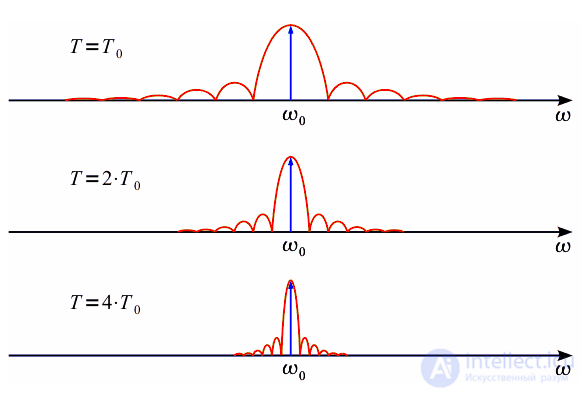
 до бесконечности, то спектр будет сужаться и стремиться к дельта-импульсу. Прямоугольный импульс
до бесконечности, то спектр будет сужаться и стремиться к дельта-импульсу. Прямоугольный импульс  назовем оконной функцией.
назовем оконной функцией.
 отсчетам сигнала
отсчетам сигнала 
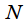 отсчетов спектра, взятых на одном периоде повторения спектра:
отсчетов спектра, взятых на одном периоде повторения спектра: 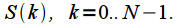 Отсчеты сигнала, взятые через равные промежутки времени
Отсчеты сигнала, взятые через равные промежутки времени 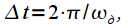 где
где 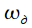 - частота дискретизации (рад/с). Таким образом интервал анализа
- частота дискретизации (рад/с). Таким образом интервал анализа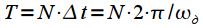 , тогда спектральные отсчеты берутся через интервал
, тогда спектральные отсчеты берутся через интервал 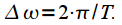 Ширина главного лепестка спектра
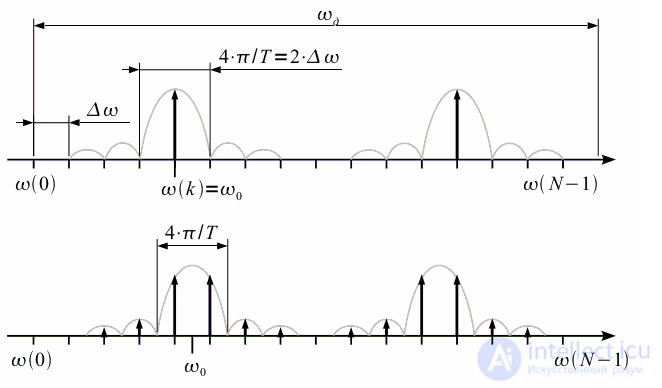
Ширина главного лепестка спектра 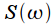 (смотри рисунок 1) равна
(смотри рисунок 1) равна 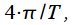 тогда можно рассмотреть два случая. Первый случай частота сигнала совпадает с
тогда можно рассмотреть два случая. Первый случай частота сигнала совпадает с 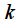 -ой частотой спектра
-ой частотой спектра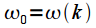 (верхний график рисунка 3). При дискретизации получим только отсчет на частоте
(верхний график рисунка 3). При дискретизации получим только отсчет на частоте 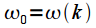 по амплитуде соответствующий амплитуде сигнала, остальные спектральные отсчеты будут равны нулю, так как моменты дискретизации спектра совпадут с нулями спектра оконной функции. Второй случай когда частота
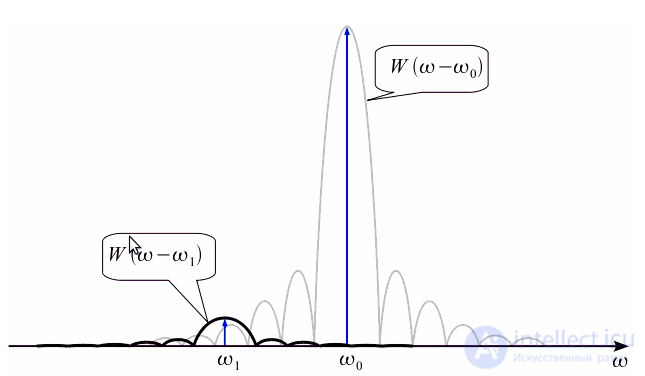
по амплитуде соответствующий амплитуде сигнала, остальные спектральные отсчеты будут равны нулю, так как моменты дискретизации спектра совпадут с нулями спектра оконной функции. Второй случай когда частота 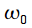 не совпадает ни с одной частотой из сетки спектральных отсчетов (нижний график рисунка 3). В этом случае спектр сигнала «размывается». Вместо одного спектрального отсчета получаем множество отсчетов, так как дискретизация производится уже не в нулях спектра функции окна, и все боковые лепестки проявляются в спектре. Кроме того амплитуда спектральных отсчетов также уменьшается.
не совпадает ни с одной частотой из сетки спектральных отсчетов (нижний график рисунка 3). В этом случае спектр сигнала «размывается». Вместо одного спектрального отсчета получаем множество отсчетов, так как дискретизация производится уже не в нулях спектра функции окна, и все боковые лепестки проявляются в спектре. Кроме того амплитуда спектральных отсчетов также уменьшается.
 и
и  , причем амплитуда сигнала на частоте
, причем амплитуда сигнала на частоте  много меньше амплитуды сигнала на частоте
много меньше амплитуды сигнала на частоте 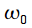 . Ограничение интервала анализа приведет к тому, что спектры «размажутся», и сигнал на частоте
. Ограничение интервала анализа приведет к тому, что спектры «размажутся», и сигнал на частоте 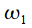 будет не заметен под боковым лепестком сигнала с частотой
будет не заметен под боковым лепестком сигнала с частотой 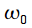 , как это показано на рисунке 4.
, как это показано на рисунке 4.
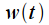 , то есть надо изменить оконную функцию, а именно сделать ее более гладкой, как это показано на рисунке 5.
, то есть надо изменить оконную функцию, а именно сделать ее более гладкой, как это показано на рисунке 5.
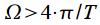 . Таким образом мы вроде бы побороли боковые лепестки, и смогли обнаружить слабые сигналы (смотри рисунок 6), которые раньше терялись в боковых лепестках, но заплатили за это расширением основного лепестка.
. Таким образом мы вроде бы побороли боковые лепестки, и смогли обнаружить слабые сигналы (смотри рисунок 6), которые раньше терялись в боковых лепестках, но заплатили за это расширением основного лепестка.
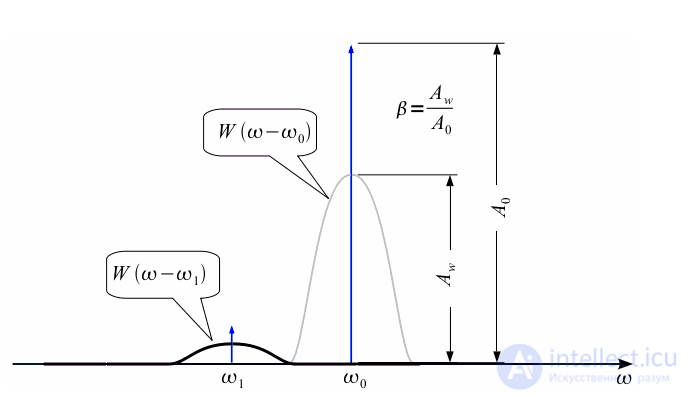
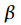 . Для пояснения коэффициента ослабления
. Для пояснения коэффициента ослабления 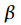 рассмотрим постоянную составляющую
рассмотрим постоянную составляющую 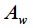 оконной функции на интервале
оконной функции на интервале  :
: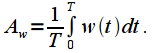 |
(2) |
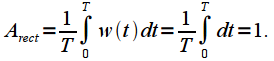 |
(3) |
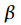 называют отношение постоянной составляющей
называют отношение постоянной составляющей 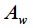 заданной функции окна, к постоянной составляющей прямоугольного окна
заданной функции окна, к постоянной составляющей прямоугольного окна  :
: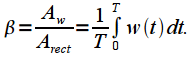 |
(4) |
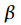 раз по сравнению с прямоугольным окном. Коэффициент ослабления выражают в логарифмической шкале:
раз по сравнению с прямоугольным окном. Коэффициент ослабления выражают в логарифмической шкале: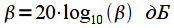 |
(5) |
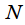 отсчетов оконной функции
отсчетов оконной функции 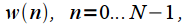 взятых через промежуток
взятых через промежуток 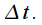 Тогда
Тогда 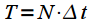 интеграл в выражении (4) заменяется на сумму:
интеграл в выражении (4) заменяется на сумму: |
(6) |
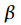 .
.
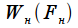 оконной функции, представленную на рисунке 7.
оконной функции, представленную на рисунке 7.
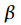 :
: 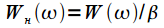 . Таким образом все АЧХ будут иметь максимум равный единице (0 дБ) на нулевой частоте. Поскольку ширина главного лепестка зависит от длительности окна во времени (смотри рисунок 2), то введена нормировка частоты:
. Таким образом все АЧХ будут иметь максимум равный единице (0 дБ) на нулевой частоте. Поскольку ширина главного лепестка зависит от длительности окна во времени (смотри рисунок 2), то введена нормировка частоты:
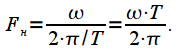 |
(7) |
 определяется как нормированная полоса при которой
определяется как нормированная полоса при которой 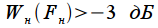 .
. . Согласно рисунку 5
. Согласно рисунку 5 .
. .
.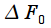 прямоугольного окна равна 2. Тогда можно ввести параметр, показывающий во сколько раз нормированная ширина главного лепестка АЧХ по нулевому уровню
прямоугольного окна равна 2. Тогда можно ввести параметр, показывающий во сколько раз нормированная ширина главного лепестка АЧХ по нулевому уровню 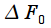 заданного окна шире чем
заданного окна шире чем 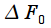 прямоугольного окна. Обозначим этот параметр как
прямоугольного окна. Обозначим этот параметр как 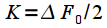 . В зависимости от параметра
. В зависимости от параметра 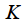 окна делят на окна высокого разрешения
окна делят на окна высокого разрешения  и окна низкого разрешения
и окна низкого разрешения 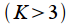 .
.
| Наименование окна | Выражение в дискретном виде: 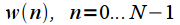 |
Примечание |
| Прямоугольное окно (rectangle window) | 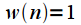 |
Окно высокого разрешения минимальная ширина главного лепестка, но максимальный уровень боковых лепестков |
| Синус-окно | 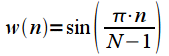 |
Окно высокого разрешения |
| Окно Ланцоша (Lanczos window), или sinc - окно | 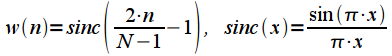 |
Окно высокого разрешения |
| Окно Барлетта (Bartlett window), или треугольное окно | 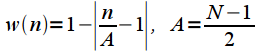 |
Окно высокого разрешения |
| Окно Ханна (Hann window) | 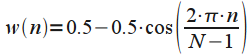 |
Окно высокого разрешения |
| Окно Барлетта — Ханна (Bartlett–Hann window) |  |
Окно высокого разрешения |
| Окно Хемминга (Hamming window) | 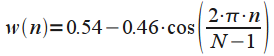 |
Окно высокого разрешения. Наилучшее окно при 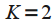 |
| Окно Блэкмана (Blackman window) | 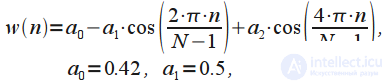 |
Окно высокого разрешения. |
| Окно Блэкмана — Харриса (Blackman–Harris window) | 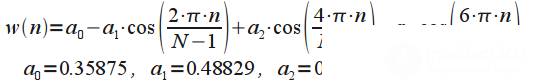 |
Окно низкого разрешения |
| Окно Наталла (Nuttall window) | 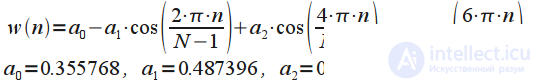 |
Окно низкого разрешения |
| Окно Блэкмана — Наталла (Blackman–Nuttall window) | 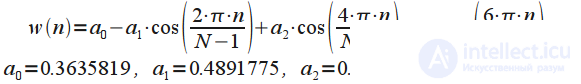 |
Окно низкого разрешения |
| Окно с плоской вершиной (Flat top window) | 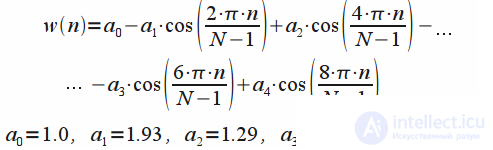 |
Окно низкого разрешения |
| Окно Гаусса (Gaussian window) | 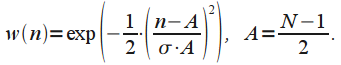 |
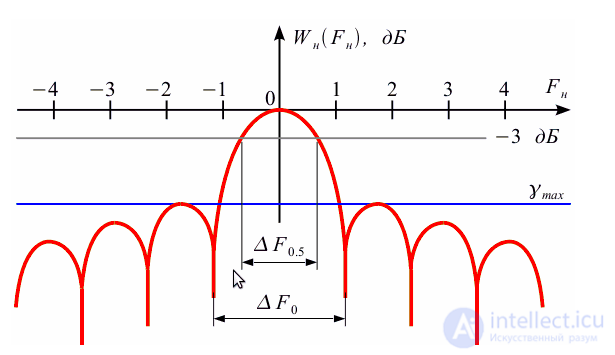
Свойства окна зависят от параметра  |
| Наименование окна | 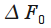 |
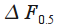 |
 |
 , дБ , дБ |
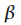 , дБ , дБ |
| Прямоугольное окно (rectangle window) | 2 | 0,89 | 1 | -13 | 0 |
| Синус-окно | 3 | 1,23 | 1,5 | -23 | -3,93 |
| Окно Ланцоша (Lanczos window), или sinc - окно | 3,24 | 1,3 | 1,62 | -26,4 | -4,6 |
| Окно Барлетта (Bartlett window), или треугольное окно | 4 | 1,33 | 2 | -26,5 | -6 |
| Окно Ханна (Hann window) | 4 | 1,5 | 2 | -31,5 | -6 |
| Окно Барлетта — Ханна (Bartlett–Hann window) | 4 | 1,45 | 2 | -35,9 | -6 |
| Окно Хемминга (Hamming window) | 4 | 1,33 | 2 | -42 | -5,37 |
| Окно Блэкмана (Blackman window) | 6 | 1,7 | 3 | -58 | -7,54 |
| Окно Блэкмана — Харриса (Blackman–Harris window) | 8 | 1,97 | 4 | -92 | -8,91 |
| Окно Наталла (Nuttall window) | 8 | 1,98 | 4 | -93 | -9 |
| Окно Блэкмана — Наталла (Blackman–Nuttall window) | 8 | 1,94 | 4 | -98 | -8,8 |
| Окно с плоской вершиной (Flat top window) | 10 | 3,86 | 5 | -69 | 0 |
Окно Гаусса (Gaussian window)  |
8 | 1,82 | 4 | -65 | -8,52 |
Окно Гаусса (Gaussian window) 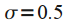 |
3,4 | 1,2 | 1,7 | -31,5 | -4,48 |
Окно Гаусса (Gaussian window)  |
2,2 | 0,94 | 1,1 | -15,5 | -0,96 |
Надеюсь, эта статья про спектральный анализ на ограниченном интервале времени оконные функции, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое спектральный анализ на ограниченном интервале времени оконные функции и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровая обработка сигналов
Комментарии
Оставить комментарий
Цифровая обработка сигналов
Термины: Цифровая обработка сигналов