Лекция
Привет, сегодня поговорим про динамический пересчет спектральных отсчетов на каждом такте дискретизации, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое динамический пересчет спектральных отсчетов на каждом такте дискретизации, модифицированный алгоритм герцеля , настоятельно рекомендую прочитать все из категории Цифровая обработка сигналов.
В данной статье мы рассмотрим довольно специфическую задачу анализа изменения заданного спектрального отсчета во времени. Такая задача актуальна при декодировании DTMF сигнала или при контроле во времени заданного набора кратных гармоник, когда использование алгоритмов БПФ нецелесообразно ввиду малого количества спектральный отсчетов.
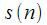 ,
, 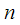 – номер отсчета. Спектральные отсчеты сигнала
– номер отсчета. Спектральные отсчеты сигнала 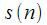 мы будем обозначать заглавной буквой
мы будем обозначать заглавной буквой 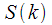 ,
, 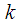 – номер спектрального отсчета соответствующий частоте
– номер спектрального отсчета соответствующий частоте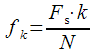 ,
, 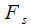 – частота дискретизации,
– частота дискретизации, 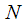 – количество точек ДПФ.
– количество точек ДПФ.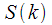
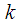 – номер спектрального отсчета . С течением времени мы получаем все новые и новые отсчеты и спектр
– номер спектрального отсчета . С течением времени мы получаем все новые и новые отсчеты и спектр 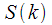 меняется. Так на рисунке 1 синим показано изменение спектра
меняется. Так на рисунке 1 синим показано изменение спектра 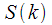 для трех временных срезов соответствующих номерам отсчетов сигнала
для трех временных срезов соответствующих номерам отсчетов сигнала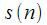 .
.

 мы можем получить частотный срез
мы можем получить частотный срез 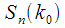 (показан красным) из которого можем проанализировать амплитуду и фазу спектрального отсчета
(показан красным) из которого можем проанализировать амплитуду и фазу спектрального отсчета 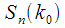 во времени. В данной статье мы будем заниматься анализом изменения заданного спектрального отсчета во времени при поступлении новых отсчетов сигнала.
во времени. В данной статье мы будем заниматься анализом изменения заданного спектрального отсчета во времени при поступлении новых отсчетов сигнала.
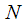 отсчетов. Мы же будем рассматривать алгоритм, который позволяет вести пересчет спектра «на лету», т. е. при поступлении каждого очередного отсчета. Мы увидим, что полученный алгоритм будет представлять собой модификацию алгоритма Герцеля для пересчета спектрального отсчета на каждом такте дискретизации
отсчетов. Мы же будем рассматривать алгоритм, который позволяет вести пересчет спектра «на лету», т. е. при поступлении каждого очередного отсчета. Мы увидим, что полученный алгоритм будет представлять собой модификацию алгоритма Герцеля для пересчета спектрального отсчета на каждом такте дискретизации
 выражение ДПФ принимает вид
выражение ДПФ принимает вид
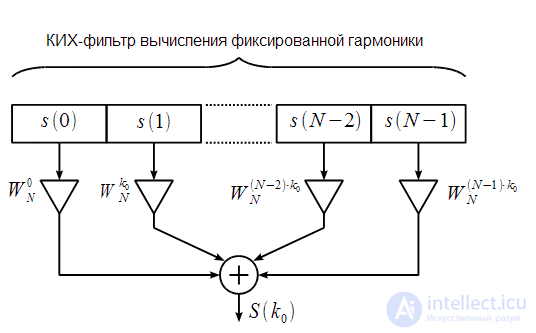
 можно осуществить при помощи структуры показанной на рисунке 2. По сути (2) это выход КИХ фильтра.
можно осуществить при помощи структуры показанной на рисунке 2. По сути (2) это выход КИХ фильтра.
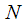 комплексных умножений и сложений.
комплексных умножений и сложений.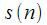 поступают в буфер длиной
поступают в буфер длиной 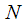 и при поступлении каждого нового отсчета
и при поступлении каждого нового отсчета 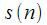 необходимо пересчитать значение фиксированной гармоники как это показано на рисунке 3. Другими словами при поступлении очередного отсчета буфер сдвигается и выход КИХ фильтра изменяется.
необходимо пересчитать значение фиксированной гармоники как это показано на рисунке 3. Другими словами при поступлении очередного отсчета буфер сдвигается и выход КИХ фильтра изменяется.

 на предыдущем такте, т. е. при поступлении отсчета исходного сигнала
на предыдущем такте, т. е. при поступлении отсчета исходного сигнала 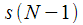 :
:
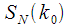 на текущем такте при поступлении отсчета исходного сигнала
на текущем такте при поступлении отсчета исходного сигнала 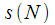 .
.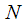 комплексных умножений и сложений, что невозможно в реальном времени при высоких частотах дискретизации. Однако из рисунка 3 можно заметить, что пересчет всего спектрального отсчета крайне неэффективен, поскольку используются те же самые отсчеты что и на предыдущем такте, за исключением
комплексных умножений и сложений, что невозможно в реальном времени при высоких частотах дискретизации. Однако из рисунка 3 можно заметить, что пересчет всего спектрального отсчета крайне неэффективен, поскольку используются те же самые отсчеты что и на предыдущем такте, за исключением 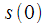 , который не участвует в расчете
, который не участвует в расчете 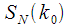 и
и 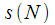 который не участвует в расчете
который не участвует в расчете  . Об этом говорит сайт https://intellect.icu . Таким образом, можно предположить, что существует способ рекуррентного пересчета спектрального отсчета на текущем и предыдущих тактах.
. Об этом говорит сайт https://intellect.icu . Таким образом, можно предположить, что существует способ рекуррентного пересчета спектрального отсчета на текущем и предыдущих тактах.
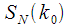 . На рисунке 4 показано, что при поступлении очередного отсчета
. На рисунке 4 показано, что при поступлении очередного отсчета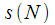 (показан зеленым), буфер сдвигается и отсчет
(показан зеленым), буфер сдвигается и отсчет 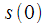 (отмечен желтым) выходит из буфера, или можно сказать, что выходит за пределы импульсной характеристики КИХ фильтра.
(отмечен желтым) выходит из буфера, или можно сказать, что выходит за пределы импульсной характеристики КИХ фильтра.


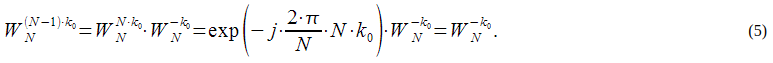

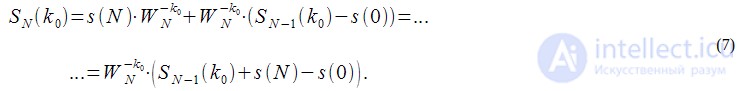
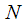 – всегда одно комплексное умножение и два сложения.
– всегда одно комплексное умножение и два сложения.
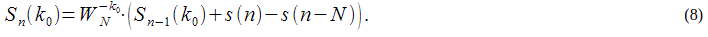
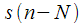 – задержанный на
– задержанный на 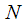 отсчетов входной сигнал
отсчетов входной сигнал 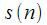 (комплексный или вещественный), в выражении (7)
(комплексный или вещественный), в выражении (7)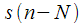 соответствует
соответствует 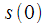 . Соотношение (7) получается из (8) при
. Соотношение (7) получается из (8) при 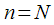 .
.


 являются комплексными.
являются комплексными.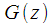 БИХ — фильтра соответствующего алгоритму Герцеля:
БИХ — фильтра соответствующего алгоритму Герцеля:
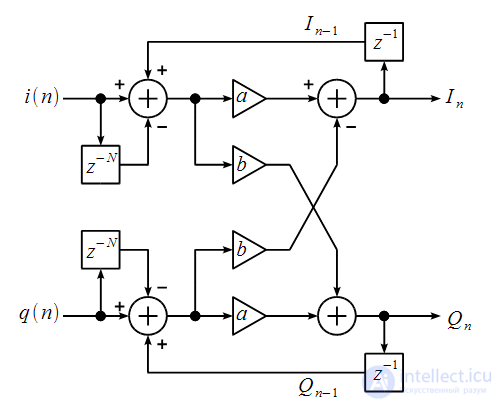
 БИХ — фильтра, который «умеет пересчитывать» предыдущее значение спектрального отсчета в текущее при поступлении очередного отсчета дискретного сигнала можно представить через передаточную характеристику БИХ — фильтра алгоритма Герцеля:
БИХ — фильтра, который «умеет пересчитывать» предыдущее значение спектрального отсчета в текущее при поступлении очередного отсчета дискретного сигнала можно представить через передаточную характеристику БИХ — фильтра алгоритма Герцеля:
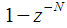 , которая позволяет вести динамический пересчет спектрального отсчета при поступлении отсчетов сигнала в реальном времени.
, которая позволяет вести динамический пересчет спектрального отсчета при поступлении отсчетов сигнала в реальном времени.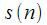 равен:
равен:

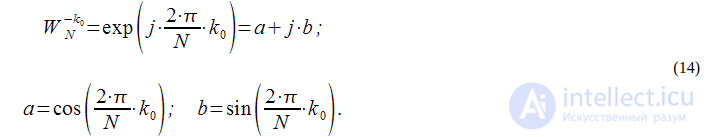

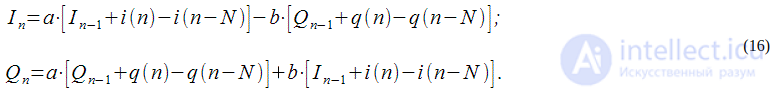
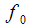 и
и  при частоте дискретизации
при частоте дискретизации 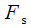 . Рассмотрим как правильно выбрать количество точек ДПФ
. Рассмотрим как правильно выбрать количество точек ДПФ 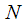 , а также номера спектральных отсчетов
, а также номера спектральных отсчетов 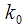 и
и 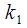 соответствующих частотам
соответствующих частотам 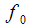 и
и  .
.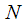 должно быть таким, чтобы частоты
должно быть таким, чтобы частоты 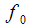 и
и  «не сливались» в одну гармонику, т.е.
«не сливались» в одну гармонику, т.е.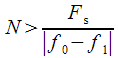 (17)
(17)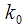 спектрального отсчета для частоты
спектрального отсчета для частоты 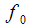 будет равен:
будет равен: (18)
(18)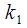 спектрального отсчета для частоты
спектрального отсчета для частоты  будет равен:
будет равен: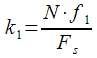 (19)
(19)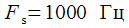 ,
,  и
и  . Тогда количество точек ДПФ должно быть:
. Тогда количество точек ДПФ должно быть: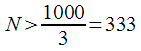 (20)
(20)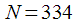 , тогда
, тогда 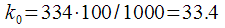 , а
, а 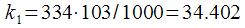 . Расположение гармоник показано на рисунке 7.
. Расположение гармоник показано на рисунке 7.
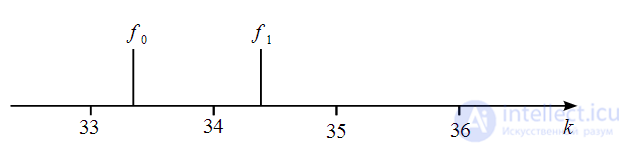
 округлить в большую сторону, тогда
округлить в большую сторону, тогда  и согласно (18)
и согласно (18) 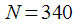 . Тогда при
. Тогда при 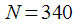
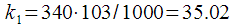 практически совпадает с 35-м номером спектрального отсчета, как это показано на рисунке 8.
практически совпадает с 35-м номером спектрального отсчета, как это показано на рисунке 8.
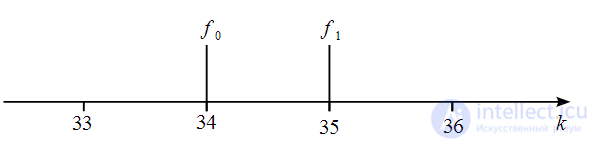
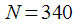 попадает целое количество периодов повторения сигнала, что уменьшит эффект растекания при расчете спектрального отсчета.
попадает целое количество периодов повторения сигнала, что уменьшит эффект растекания при расчете спектрального отсчета.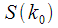 и
и 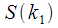 при чередовании сигналов с частотами
при чередовании сигналов с частотами и
и  , частотой дискретизации
, частотой дискретизации 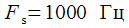 и
и 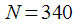 . Частоты
. Частоты  и
и сменяют друг друга каждую секунду.
сменяют друг друга каждую секунду.

 . Это необходимо учитывать при обработке.
. Это необходимо учитывать при обработке.
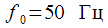 .
.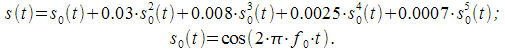 (21)
(21) на выходе нелинейного элемента. Частота дискретизации равна
на выходе нелинейного элемента. Частота дискретизации равна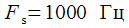 .
.
 .
.
 (22)
(22) точек. Тогда номера спектральных отсчетов соответствующих первым четырем гармоникам
точек. Тогда номера спектральных отсчетов соответствующих первым четырем гармоникам  равны:
равны:
 , а на рисунке 12 – оценка амплитуд первых четырех гармоник при помощи модифицированного алгоритма Герцеля.
, а на рисунке 12 – оценка амплитуд первых четырех гармоник при помощи модифицированного алгоритма Герцеля.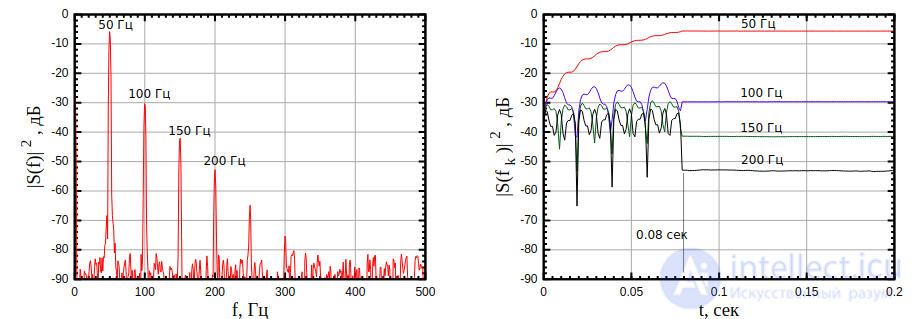
Рисунок 11: Спектр сигнала на выходе нелинейного элемента
Рисунок 12: Динамическое сопровождение амплитуд кратных гармоник сигнала
 точек модифицированный алгоритм полностью повторяет алгоритм Герцеля, но после того как буфер полностью заполнен, и нерекурсивная ветвь БИХ — фильтра начинает работать мы получаем динамический пересчет амплитуд гармоник на каждом такте дискретизации. Это позволяет нам вести непрерывное сопровождение амплитуд кратных гармоник на выходе нелинейного элемента. Измеренные амплитуды точно равны амплитудам гармоник показанным на рисунке 11, но мы можем наблюдать их изменение во времени как это показано на трехмерной проекции (рисунок 1).
точек модифицированный алгоритм полностью повторяет алгоритм Герцеля, но после того как буфер полностью заполнен, и нерекурсивная ветвь БИХ — фильтра начинает работать мы получаем динамический пересчет амплитуд гармоник на каждом такте дискретизации. Это позволяет нам вести непрерывное сопровождение амплитуд кратных гармоник на выходе нелинейного элемента. Измеренные амплитуды точно равны амплитудам гармоник показанным на рисунке 11, но мы можем наблюдать их изменение во времени как это показано на трехмерной проекции (рисунок 1).
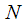 отсчетов к БИХ — фильтру алгоритма Герцеля и позволяет учесть все промежуточные результаты при расчете заданной гармоники спектра сигнала. Также показаны примеры выбора длины буфера
отсчетов к БИХ — фильтру алгоритма Герцеля и позволяет учесть все промежуточные результаты при расчете заданной гармоники спектра сигнала. Также показаны примеры выбора длины буфера 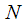 при анализе двух спектральных составляющих, а также гармоник кратной частоты на выходе нелинейного элемента.
при анализе двух спектральных составляющих, а также гармоник кратной частоты на выходе нелинейного элемента.Надеюсь, эта статья про динамический пересчет спектральных отсчетов на каждом такте дискретизации, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое динамический пересчет спектральных отсчетов на каждом такте дискретизации, модифицированный алгоритм герцеля и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровая обработка сигналов
Комментарии
Оставить комментарий
Цифровая обработка сигналов
Термины: Цифровая обработка сигналов