Лекция
Привет, сегодня поговорим про линейная свертка, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое линейная свертка, циклическая свертка , настоятельно рекомендую прочитать все из категории Цифровая обработка сигналов.
Свертка — операция в функциональном анализе, которая при применении к двум функциям и
возвращает третью функцию, соответствующую взаимнокорреляционной функции
и
. Операцию свертки можно интерпретировать как «схожесть» одной функции с отраженной и сдвинутой копией другой. Понятие свертки обобщается для функций, определенных на произвольных измеримых пространствах и может рассматриваться как особый вид интегрального преобразования.
Свертка последовательностей — это результат перемножения элементов двух заданных числовых последовательностей таким образом, что члены одной последовательности берутся с возрастанием индексов, а члены другой — с убыванием (что и служит основанием для принятого названия данной операции).
Свертка последовательностей — это частный случай свертки функций.
Свертка является линейным преобразованием входящих в нее последовательностей.
Свертку двух заданных последовательностей можно получить, если, сначала, использовать для каждой последовательности дискретное преобразование Фурье (ДПФ), затем перемножить результаты преобразования и произвести обратное дискретное преобразование Фурье (обратное ДПФ). Это важное свойство находит свое широкое применение в цифровой обработке сигналов.
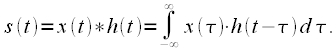 (1)
(1)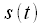 на выходе линейного фильтра с импульсной характеристикой
на выходе линейного фильтра с импульсной характеристикой 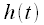 , при входном сигнале
, при входном сигнале 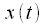 .
.К традиционным типам сверток относятся:
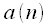 ,
,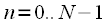 , и
, и  ,
,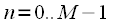 . В общем случае длины этих сигналов
. В общем случае длины этих сигналов 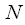 и
и  могут отличаться. Линейной сверткой сигналов
могут отличаться. Линейной сверткой сигналов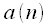 и
и называется дискретный сигнал вида:
называется дискретный сигнал вида: (2)
(2)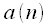 и
и сдвигают относительно друг друга почленно перемножают и складывают. При этом предполагается, что
сдвигают относительно друг друга почленно перемножают и складывают. При этом предполагается, что 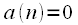 при
при 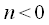 и
и 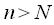 , а также
, а также 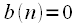 при
при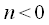 и
и 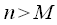

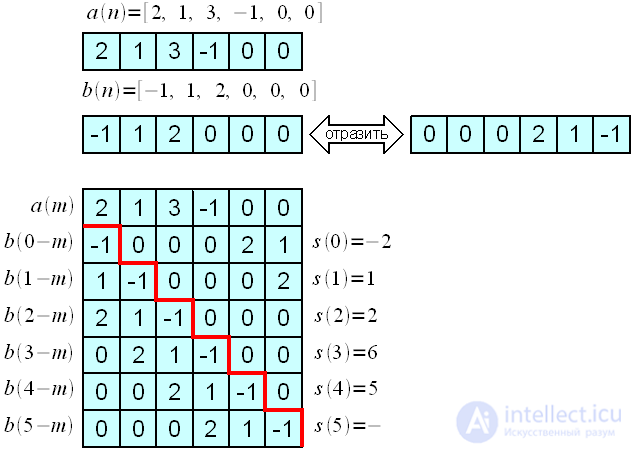
 сдвигаются относительно отсчетов последовательности
сдвигаются относительно отсчетов последовательности 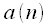 все возможные перекрывающиеся отсчеты почленно перемножаются и складываются.
все возможные перекрывающиеся отсчеты почленно перемножаются и складываются.
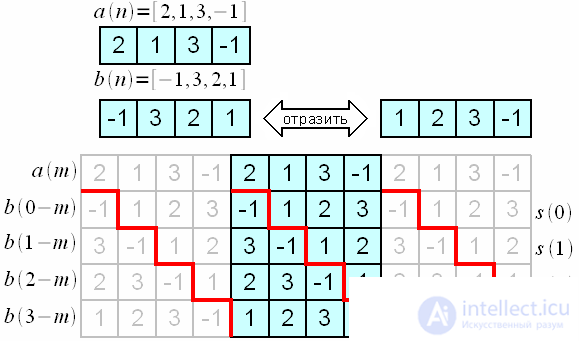
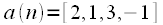 длиной 4 отсчета и
длиной 4 отсчета и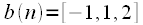 длиной 3 отсчета.
длиной 3 отсчета.
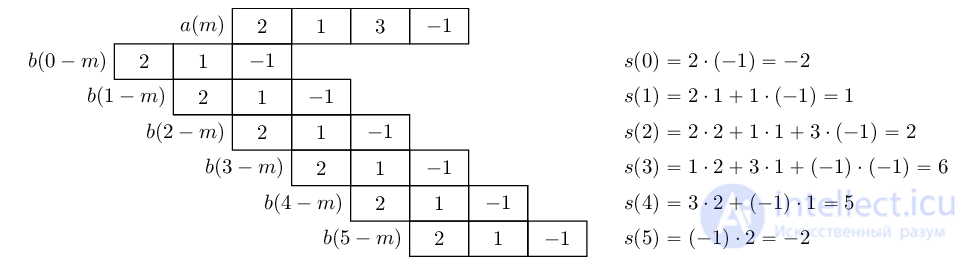
 при вычислении свертки отражается слева-направо, поскольку
при вычислении свертки отражается слева-направо, поскольку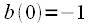 самый первый отсчет (самый ранний по времени) и обрабатываться он также должен первым.
самый первый отсчет (самый ранний по времени) и обрабатываться он также должен первым.
Линейная свертка описывает прохождение сигнала 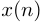 ,
, 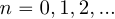 через КИХ-фильтр порядка
через КИХ-фильтр порядка 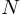 с импульсной характеристикой
с импульсной характеристикой 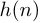 ,
,  :
:
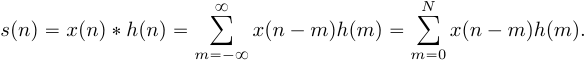
В выражении (5) пределы суммирования соответствуют длительности импульсной характеристики КИХ фильтра, так как 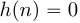 при
при 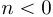 и
и  .
.
Другим важнейшим прикладным значением линейной свертки является расчет произведения полиномов.
Пусть значения дискретной последовательности 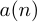 ,
, 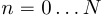 , содержащей
, содержащей 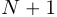 значение представляет собой коэффициенты полинома
значение представляет собой коэффициенты полинома 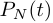 :
:
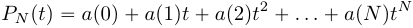 (6)
(6)степени 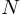 , а значения дискретной последовательности
, а значения дискретной последовательности 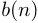 ,
, 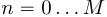 — содержит
— содержит 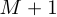 коэффициентов полинома
коэффициентов полинома
 (7)
(7)степени 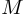 . Тогда коэффициенты произведения полиномов
. Тогда коэффициенты произведения полиномов 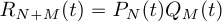 будут равны линейной свертке
будут равны линейной свертке 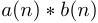 . В результате мы получим
. В результате мы получим 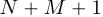 коэффициент полинома
коэффициент полинома 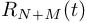 степени
степени  .
.
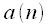 и
и 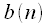 - периодические с одинаковым периодом
- периодические с одинаковым периодом 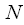 отсчетов. Тогда круговой сверткой сигналов
отсчетов. Тогда круговой сверткой сигналов 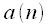 и
и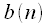 называется сигнал вида:
называется сигнал вида: (3)
(3)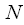 отсчетов.
отсчетов.Пусть имеется две последовательности 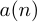 и
и 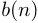 ,
, 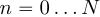 одинаковой длительности
одинаковой длительности 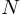 отсчетов. Циклической сверткой называется последовательность
отсчетов. Циклической сверткой называется последовательность 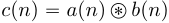 вида:
вида:

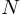 отсчетов, причем результатом также будет последовательность длины
отсчетов, причем результатом также будет последовательность длины 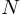 .
.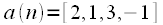 и
и 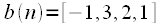 .
.
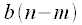 . Заметим, что в силу периодичности сигналов
. Заметим, что в силу периодичности сигналов 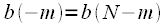 .
.
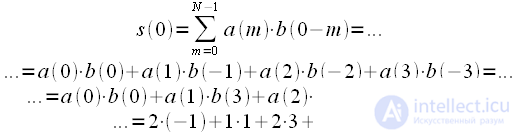 (4)
(4)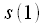 :
: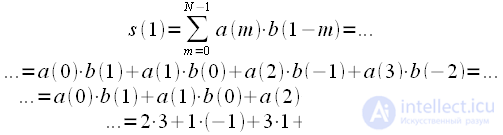 (5)
(5)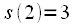 и
и 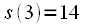 .
.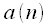 и
и длительностью
длительностью 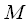 и
и 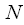 отсчетов соответственно дополнить нулями до длины
отсчетов соответственно дополнить нулями до длины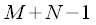 .
.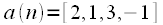 длиной 4 отсчета и
длиной 4 отсчета и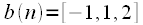 длиной 3 отсчета (этот пример был рассмотрен выше).
длиной 3 отсчета (этот пример был рассмотрен выше).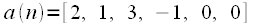 и
и 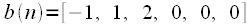 , так чтобы в каждой последовательности было по 6 отсчетов.
, так чтобы в каждой последовательности было по 6 отсчетов.
 умножений,
умножений,  и
и 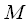 – длины сворачиваемых сигналов, а при вычислении линейной свертки через циклическую
– длины сворачиваемых сигналов, а при вычислении линейной свертки через циклическую 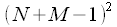 умножений и сложений. Однако рассмотрим дискретное преобразование Фурье от циклической свертки:
умножений и сложений. Однако рассмотрим дискретное преобразование Фурье от циклической свертки: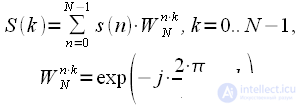 (6)
(6)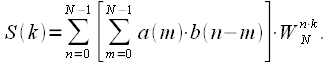 (7)
(7)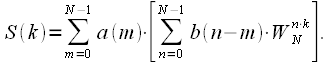 (8)
(8)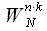 в виде:
в виде: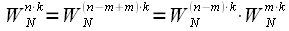 (9)
(9)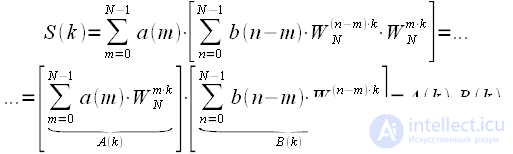 (10)
(10)
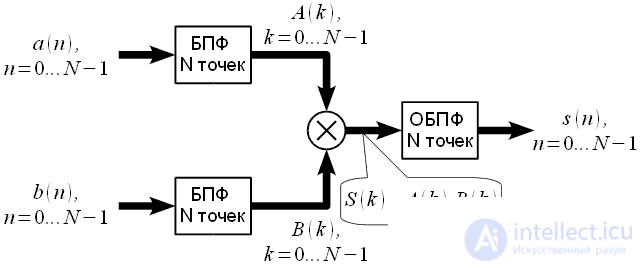
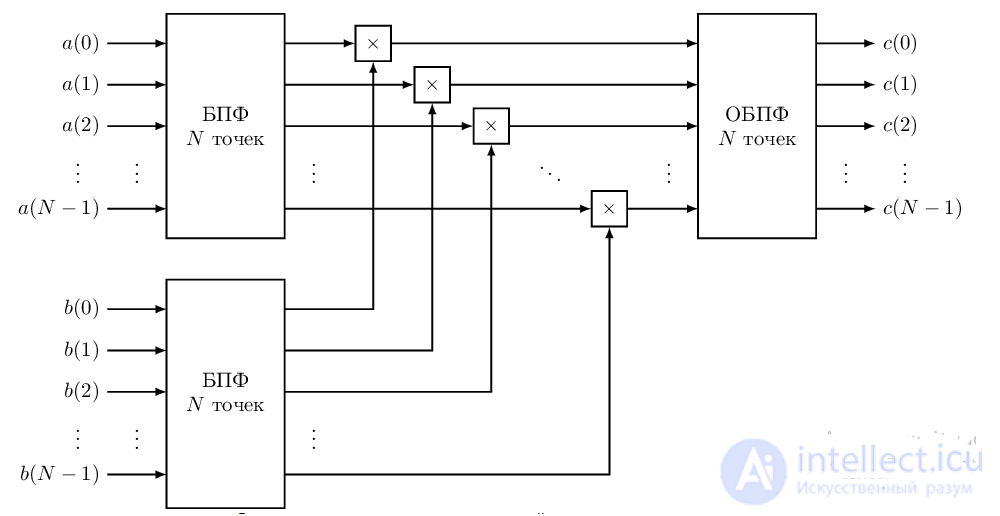
 , то можно предложить следующий метод вычисления циклической свертки. Исходные последовательности
, то можно предложить следующий метод вычисления циклической свертки. Исходные последовательности  и
и 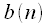 ,
, 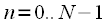 можно дополнить нулями до длины
можно дополнить нулями до длины 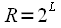 , поскольку для длин равных целой степени двойки разработаны эффективные алгоритмы БПФ, после этого применяем схему вычисления свертки, представленную на рисунке 5. На выходе получим
, поскольку для длин равных целой степени двойки разработаны эффективные алгоритмы БПФ, после этого применяем схему вычисления свертки, представленную на рисунке 5. На выходе получим 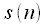 ,
,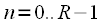 , из которого надо взять только первые
, из которого надо взять только первые 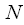 отсчетов.
отсчетов.
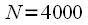 , а
, а 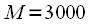 . Прямое вычисление линейной свертки потребует
. Прямое вычисление линейной свертки потребует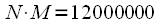 (12 миллионов) операций умножения и сложения.
(12 миллионов) операций умножения и сложения.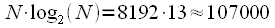 операций комплексного умножения или 428000 операций действительного умножения. Таких блоков БПФ будет всего 3 штуки, плюс надо учесть 8192 комплексных умножений спектров, итого
операций комплексного умножения или 428000 операций действительного умножения. Таких блоков БПФ будет всего 3 штуки, плюс надо учесть 8192 комплексных умножений спектров, итого 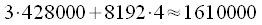 , что почти в 7.5 раз ниже чем если бы мы считали линейную свертку в лоб.
, что почти в 7.5 раз ниже чем если бы мы считали линейную свертку в лоб.Вычислительные преимущества, которые мы получаем при использовании аппарата БПФ для расчета циклической свертки, хотелось бы также получать и для расчета линейной свертки. С этой целью рассмотрим способ приведения линейной свертки последовательностей ограниченной длительности к циклической.
Пусть 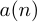 и
и 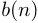 — дискретные последовательности длительности
— дискретные последовательности длительности 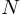 и
и 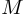 отсчетов соответственно. Линейная свертка последовательностей
отсчетов соответственно. Линейная свертка последовательностей 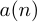 и
и 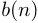 вернет
вернет 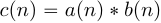 длительности
длительности 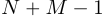 отсчет. Если мы хотим получить
отсчет. Если мы хотим получить 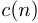 как результат циклической свертки, то необходимо дополнить
как результат циклической свертки, то необходимо дополнить 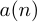 и
и 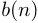 до длины
до длины 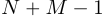 отсчет, как это показано на рисунке 7.
отсчет, как это показано на рисунке 7.
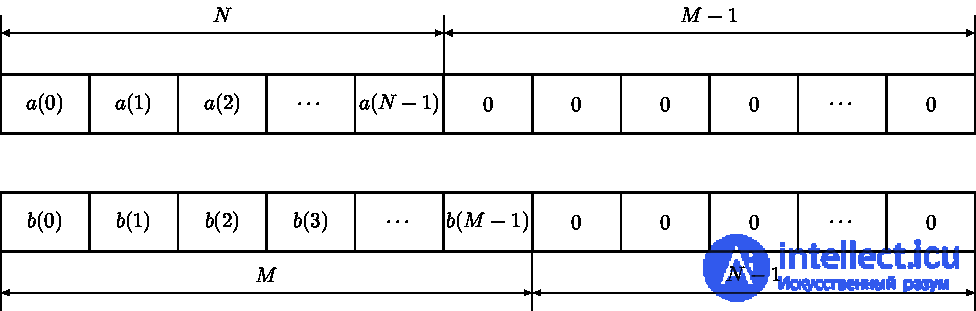
К последовательности 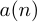 необходимо добавить
необходимо добавить 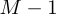 ноль, а к последовательности
ноль, а к последовательности 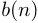 —
— 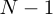 ноль. такое добавление нулей обеспечит увеличение периодичности циклического буфера до размера, когда
ноль. такое добавление нулей обеспечит увеличение периодичности циклического буфера до размера, когда 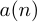 и
и 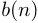 перестанут перекрываться циклически. В результате циклическая свертка будет иметь вид:
перестанут перекрываться циклически. В результате циклическая свертка будет иметь вид:
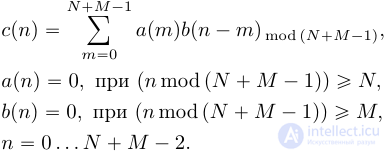
Можно показать, что циклическая свертка (15) дополненных нулями последовательностей, соответствует расчету линейной свертки исходных сигналов. Чтобы убедиться в этом, достаточно использовать матричную запись циклической свертки, и расписать соответствующие элементы 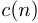 ,
, 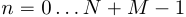 . В результате выражения
. В результате выражения 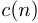 будут соответствовать линейной свертке.
будут соответствовать линейной свертке.
Необходимо заметить, что добивать 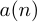 и
и 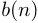 нулями можно не только до длины
нулями можно не только до длины 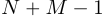 , но и до любой длины
, но и до любой длины 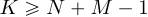 . В результате вычисления циклической свертки дополненных нулями последовательностей до длины
. В результате вычисления циклической свертки дополненных нулями последовательностей до длины 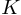 , первый
, первый 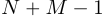 значение на выходе будет представлять собой линейную свертку, а остальные значения будут нулевыми. Это можно использовать для дополнения исходных последовательностей нулями до длины, которая допускает использование эффективных БПФ алгоритмов.
значение на выходе будет представлять собой линейную свертку, а остальные значения будут нулевыми. Это можно использовать для дополнения исходных последовательностей нулями до длины, которая допускает использование эффективных БПФ алгоритмов.
Например при 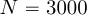 и
и  , необходимо дополнить
, необходимо дополнить 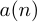 и
и 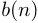 нулями до длины
нулями до длины 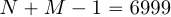 . Однако мы можем дополнить их до длины
. Однако мы можем дополнить их до длины 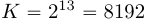 отсчетов и использовать БПФ по основанию два для расчета циклической свертки. При этом первые 6999 отсчетов результата циклической свертки будут представлять собой линейную свертку при
отсчетов и использовать БПФ по основанию два для расчета циклической свертки. При этом первые 6999 отсчетов результата циклической свертки будут представлять собой линейную свертку при 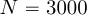 и
и  . Использование алгоритма БПФ для
. Использование алгоритма БПФ для 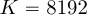 приведет к десятикратному снижению требуемых вещественных умножителей при вычислении линейной свертки при
приведет к десятикратному снижению требуемых вещественных умножителей при вычислении линейной свертки при 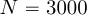 и
и  .
.
Сверточные коды позволяют исправлять пакеты ошибок путем введения в код цифр контроля четности. Выходы триггеров регистра сдвига обеспечивают задержки и подаются в отводы, после чего соответствующим образом объединяются с использованием сумматоров по модулю 2. В результате получается несколько выходов, которые последовательно считываются в каждом такте (рис. 5.39). Система является причинной и нерекурсивной, производит выход, который зависит от ее предыдущих входов, и сворачивает новые входные данные со своей импульсной характеристикой.

Рис. 5.39. Сверточный кодер
Вход всех систем сворачивается с импульсной характеристикой системы и может искажать выход. Это происходит, например, в системах телекоммуникаций и может принуждать использовать эквалайзер — линейный фильтр, который по выходу восстанавливает исходный сигнал. Перед тем как разрабатывать подобный фильтр, необходимо определить импульсную характеристику системы (идентифицировать систему). Тема идентификации системы подробно рассмотрена в работе [Proakis J. G. and Manolakis D. G. (1988) Introduction to Digital Signal Processing, p. 429. Basingstoke: Macmillan].
Тема анализа и кодирования речи в сферах взаимодействия человека с машиной и сжатия данных довольно интересна. Иногда при этом используется тот факт, что речевой сигнал можно смоделировать как свертку серии импульсов, представляющих основные тоны, активирующих импульсов и импульсной характеристики речевого тракта [Rabiner L. R. and Gold B. (1975) Theory and Application of Digital Signal Processing, Chapters 12 and 13. Englewood Cliffs NJ: Prentice-Hall]. Получающуюся тройную свертку можно легко обратить в форму, подходящую для линейной независимой от времени системы.
Для двух последовательностей данных можно легко найти их свертку, причем вычисления будут отличаться только порядком одной последовательности. Более того, для более длинных последовательностей данных необходимые операции можно ускорить, используя методы быстрого преобразования Фурье, чтобы получить быструю свертку. Если одна последовательность имеет чересчур большую длину, можно использовать методы наложения-сложения или наложения-записи; см. разделы работы [
Brigham E. O. (1974) The Fast Fourier Transform, Sections 13.3 and 13.4. Englewood Cliffs NJ: PrenticeHall.
DeFatta D. J., Lucas J. G. and Hodgkiss W. S. (1988) Digital Signal Processing: A System Design Approach, Section 6.9, p. 306. New York: Wiley.
]. Свертку можно выполнять, используя, например, КИХ-фильтр, реализуемый с помощью БПФ, а также применяя согласованный фильтр.
В сфере цифровой обработки для реализации трансверсальных фильтров может использоваться технология приборов с зарядовой связью (ПЗС). Это позволяет получать линейную фазовую характеристику при скоростях передачи данных, превышающих 100 МГц при стандартных конфигурациях линий задержки .
Аналоговую обработку можно выполнять, реализовав линии задержки с отводами, используя устройства с поверхностными акустическими волнами (ПАВ) . Эти устройства работают в диапазоне от 2 МГц до 2 ГГц. Другие реализации можно получить на основе конвольверов и корреляторов, универсальных цифровых процессоров сигналов, стандартных микропроцессоров и транспьютеров.
В качестве примеров последних можно привести системы реального времени для устранения окулярных артефактов из всех 16 каналов ЭКГ человека .
Время вычислений, необходимых для быстрой корреляции и свертки, можно дополнительно сократить в два раза . Рассмотрим свертку x(n) и h(n). При вычислении X(k) действительная часть БПФ заполняется четными членами x(n), а мнимая часть — нечетными, и длина БПФ вполовину сокращается. Далее действительная часть 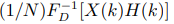 дает четные члены искомой сверткой, а мнимая часть — нечетные. Аналогично свертку двух последовательностей данных
дает четные члены искомой сверткой, а мнимая часть — нечетные. Аналогично свертку двух последовательностей данных 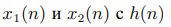 можно вычислить одновременно. Заполним действительную часть БПФ элементами последовательности x1(n), а мнимую часть — элементами последовательности x2(n) и вычислим X1 (k). Действительная часть
можно вычислить одновременно. Заполним действительную часть БПФ элементами последовательности x1(n), а мнимую часть — элементами последовательности x2(n) и вычислим X1 (k). Действительная часть 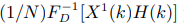 равна
равна  , а мнимая часть —
, а мнимая часть —  .
.
Пример реализации свертки, написанный на C++:

Надеюсь, эта статья про линейная свертка, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое линейная свертка, циклическая свертка и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровая обработка сигналов
Комментарии
Оставить комментарий
Цифровая обработка сигналов
Термины: Цифровая обработка сигналов