Привет, сегодня поговорим про алгоритм герцеля goertzel algorithm , обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое
алгоритм герцеля goertzel algorithm , настоятельно рекомендую прочитать все из категории Цифровая обработка сигналов.
Содержание
Введение
Рекуррентное соотношения для расчета фиксированного спектрального отсчета сигнала
Алгоритм Герцеля
Пример использования алгоритма Герцеля
Выводы
Введение
Ранее мы рассмотрели дискретное преобразование Фурье (ДПФ) и его свойства, а также алгоритмы быстрого преобразования Фурье (БПФ). Мы выяснили, что алгоритмы БПФ позволяют существенно экономить вычислительные ресурсы при расчете ДПФ. Однако часто требуется произвести расчет не всего ДПФ, а лишь фиксированного количества спектральных отсчетов. Например такая задача встает при декодировании DTMF сигналов. В этом случае применение алгоритмов БПФ может оказаться не эффективным, поскольку для получения одного спектрального отсчета потребуется произвести расчет всего ДПФ.
В данной статье мы рассмотрим алгоритм Герцеля расчета дискретного преобразования Фурье, который нашел широкое применение в задачах декодирования DTMF сигналов. Данный алгоритм позволяет эффективно рассчитывать фиксированные спектральные отсчеты ДПФ без необходимости рассчитать все ДПФ. Как будет показано ниже алгоритм Герцеля представляет собой реализацию ДПФ в виде БИХ — фильтра, что упрощает его аппаратную реализацию.
Рекуррентное соотношение для расчета фиксированного спектрального отсчета сигнала
Выражение для дискретного
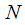
– точечного преобразования Фурье сигнала
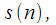
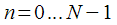
имеет вид:
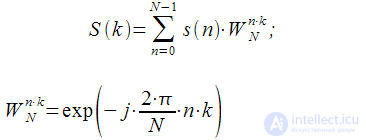 |
(1) |
Поворотные коэффициенты
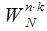
обладают следующим свойством:
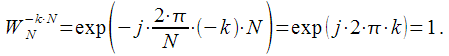 |
(2) |
Таким образом, умножение выражения (1) на
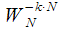
не приводит к изменению результата:
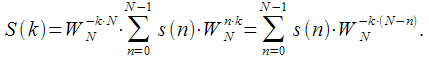 |
(3) |
Распишем сумму (3):
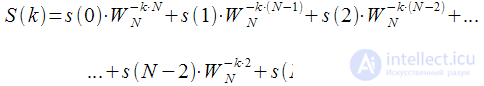 |
(4) |
Обозначим
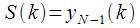
, для фиксированного номера спектрального отсчета

, кроме того вынесем в (4)
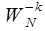
за скобки и получим:
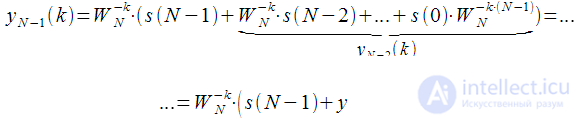 |
(5) |
Внутри скобок в выражении (5) можно выделить
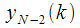
, в котором также можно вынести
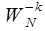
за скобки:
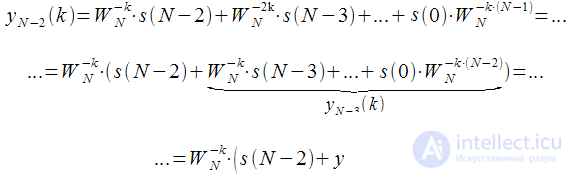 |
(6) |
Теперь получили что
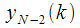
может быть получено через
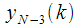
, в котором снова можно
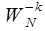
вынести за скобки. Таким образом, мы получили рекуррентное соотношение для вычисления
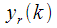
на любом шаге
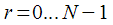
через
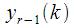
полученных на предыдущем шаге для фиксированного номера спектрального отсчета

:
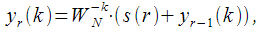 |
(7) |
где
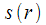
– отсчет входного сигнала с номером

. Данное рекуррентное соотношение на шаге с номером

приводит нас к
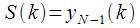
, т.е. Об этом говорит сайт https://intellect.icu . на
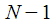
-ом шаге мы получим спектральный отсчет с номером

. Проанализировав (7), можно заметить, что рекуррентное соотношение можно трактовать как разностное уравнение БИХ-фильтра с комплексным коэффициентом
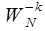
, структурная схема которого приведена на рисунке 1 .
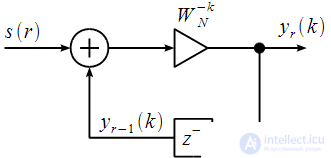
Рисунок 1: Структурная схема БИХ-фильтра реализующего расчет спектрального отсчета с номером k
Обозначив через
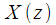
и
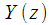
z – образы
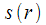
и
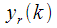
соответственно, выражение (7) можно представить в виде:
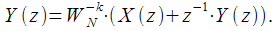 |
(8) |
Из (8) можно получить передаточную характеристику БИХ – фильтра
 |
(9) |
Теперь самое время проанализировать к чему привели нас все предыдущие рассуждения.
Напомню, что мы зафиксировали номер спектрального отсчета

и преобразовали выражение ДПФ для одного фиксированного спектрального отсчета к рекуррентному соотношению, которое позволяет нам на
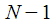
-м шаге получить значение искомого

-го спектрального отсчета
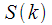
. При этом все промежуточные значения рекуррентного соотношения
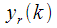
нас не интересуют, а интересует только
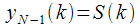
. Это важно и пригодится нам в дальнейшем. После мы рекуррентное соотношение трактовали как разностное уравнение БИХ фильтра с передаточной характеристикой (9). В результате мы получили «хитроумный фильтр» с комплексным коэффициентом
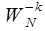
применение которого на
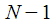
-ой итерации на выходе дает
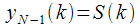
. При фиксированном

значение комплексного коэффициента
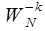
всегда постоянно.
Алгоритм Герцеля
Для вычисления одного спектрального отсчета
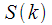
при использовании БИХ — фильтра требуется
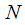
комплексных умножений и сложений, что не дает никаких преимуществ по сравнению с вычислением ДПФ «в лоб» согласно выражению (1).
Однако сокращение вычислений можно получить, если домножить числитель и знаменатель передаточной характеристики БИХ фильтра (9) на

:
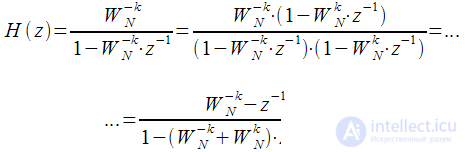 |
(10) |
Рассмотрим более подробно сумму:
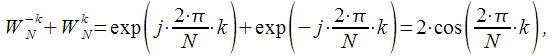 |
(11) |
тогда (10) с учетом(11) можно записать:
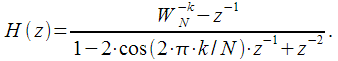 |
(12) |
Структурная схема БИХ — фильтра второго порядка, соответствующего (12) показана на рисунке 2 (подробно структурные схемы БИХ — фильтров были рассмотрены здесь), где
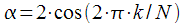
.
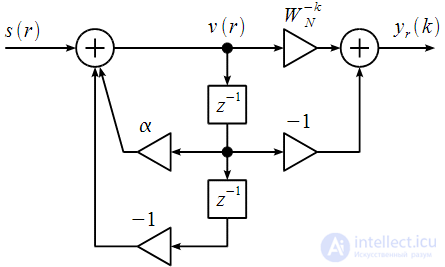
Рисунок 2: Структурная схема БИХ - фильтра 2-го порядка
Обратим внимание, что
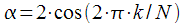
– вещественный коэффициент, соответственно умножения в рекурсивной ветви фильтра стали вещественными, причем умножения на -1 можно не учитывать. У нас остался один комплексный коэффициент
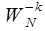
в числителе передаточной характеристики. Но мы выяснили, что промежуточные значения
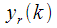
нам не важны, соответственно умножать на
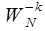
можно только на
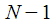
итерации, когда рассчитывается непосредственно
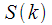
, поскольку на промежуточные значения
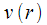
это никак не повлияет. Таким образом применение фильтра второго порядка позволяет рассчитать
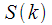
для фиксированного

с использованием
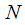
умножений, но не комплексных, а вещественных, что приводит к сокращению вычислений в 2 раза (одно комплексное умножение требует два вещественных), плюс одно комплексное умножение на
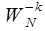
на последней итерации при расчете непосредственно
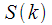
.
Исходя из рисунка 2 спектральный отсчет
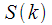
равен:
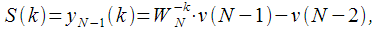 |
(13) |
где
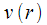
– промежуточные значения (смотри рисунок 2), которые рассчитываются итерационно:
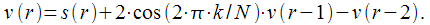 |
(14) |
Таким образом алгоритм сводится к итерационному расчету
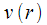
согласно (14), после чего последние два значения
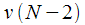
и
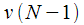
используются для расчета спектрального отсчета
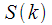
.
Пример использования алгоритма Герцеля
Пусть
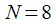
, исходный сигнал
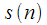
показан на рисунке 3.

Рисунок 3: Исходный сигнал
Рассчитаем при помощи алгоритма Герцеля спектральный отсчет
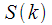
с номером
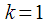
. Предварительно рассчитаем коэффициент
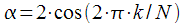
и
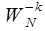
:
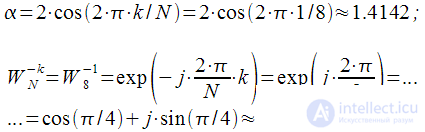 |
(15) |
В качестве начальных условий расчета зададим:
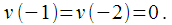 |
(16) |
Произведем итерационный расчет
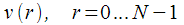
согласно (14):
 |
(17) |
Тогда согласно выражению (13) можно получить значения для спектрального отсчета :
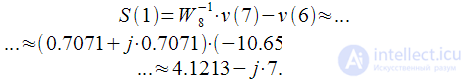 |
(18) |
Вы можете самостоятельно удостовериться, что полученное значение
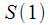
полностью соответствует результату ДПФ.
Ниже приведен исходный код программы на языке си, производящий расчет спектрального отсчета
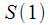
согласно рассмотренному примеру.
#include < stdio.h >
#include < stdlib.h >
#define _USE_MATH_DEFINES
#include < math.h >
int main(){
// исходные данные
int N = 8; //точек ДПФ
int k = 1; //номер спектрального отсчта
//исходный сигнал
double s[8] = {3, 2, 1, -1, 1, -2, -3, -2};
//массив промежуточных результатов
double v[8] = {0, 0, 0, 0, 0, 0, 0, 0};
//параметр альфа
double a = 2*cos(2*M_PI*k/N);
//поворотный к-т W_N^-k
double wr = cos(2*M_PI*k/N); //реальная часть
double wi = sin(2*M_PI*k/N); //мнимая часть
//учет v[-1] = v[-2] = 0
v[0] = s[0];
v[1] = s[1]+a*v[0];
// итерационный расчет массива v согласно (14)
for(int i = 2; i < N; i++)
v[i] = s[i] + a*v[i-1] - v[i-2];
//реальная и мнимая части спектрального отсчета S(1) согласно (13)
double SR = v[N-1]*wr-v[N-2];
double SI = v[N-1]*wi;
//печать результата
printf("S(%d) = %.4f%+.4fj\n",k,SR,SI);
system("Pause");
return 0;
}
Выводы
Фильтр показанный на рисунке 2 реализует расчет спектрального отсчета с номером

. Для реализации расчета всех
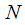
спектральных отсчетов, необходимо параллельно поставить
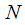
таких фильтров. Преимущество алгоритма Герцеля заключается в том, что каждый спектральный отсчет рассчитывается независимо от других, и не нужно считать все ДПФ ради нескольких отсчетов. Это широко применяется при декодировании DTMF сигналов когда анализируется амплитуда нескольких гармоник сигнала. Но алгоритм Герцеля также обладает недостатком. Для расчета одного спектрального отсчета требуется
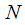
итераций, причем промежуточные значения
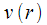
, кроме двух последних, не несут полезной информации, но их приходится рассчитывать. Алгоритм Герцеля малопривлекателен для расчета всех спектральных отсчетов ДПФ ввиду высокой вычислительной сложности. Для расчета «полного» ДПФ гораздо лучше подходят алгоритмы быстрого преобразования Фурье.
Надеюсь, эта статья про алгоритм герцеля goertzel algorithm , была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое алгоритм герцеля goertzel algorithm
и для чего все это нужно, а если не понял, или есть замечания,
то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Цифровая обработка сигналов
Из статьи мы узнали кратко, но содержательно про алгоритм герцеля goertzel algorithm
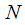 – точечного преобразования Фурье сигнала
– точечного преобразования Фурье сигнала 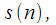
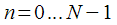 имеет вид:
имеет вид: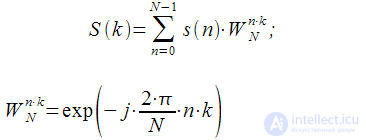
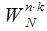 обладают следующим свойством:
обладают следующим свойством: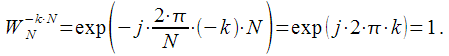
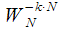 не приводит к изменению результата:
не приводит к изменению результата: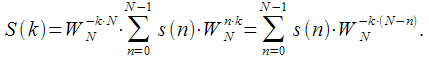
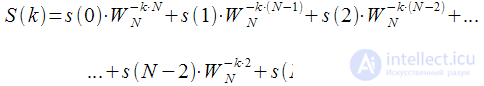
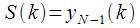 , для фиксированного номера спектрального отсчета
, для фиксированного номера спектрального отсчета  , кроме того вынесем в (4)
, кроме того вынесем в (4) 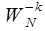 за скобки и получим:
за скобки и получим: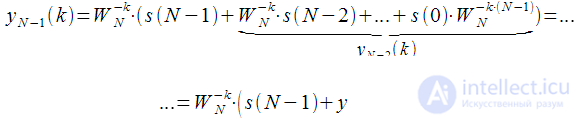
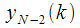 , в котором также можно вынести
, в котором также можно вынести 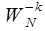 за скобки:
за скобки: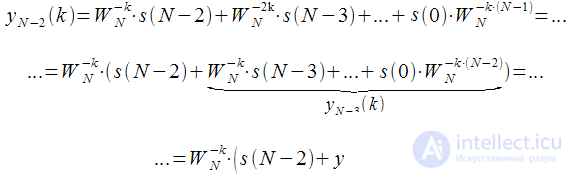
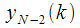 может быть получено через
может быть получено через 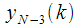 , в котором снова можно
, в котором снова можно 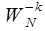 вынести за скобки. Таким образом, мы получили рекуррентное соотношение для вычисления
вынести за скобки. Таким образом, мы получили рекуррентное соотношение для вычисления 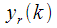 на любом шаге
на любом шаге 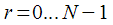 через
через 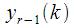 полученных на предыдущем шаге для фиксированного номера спектрального отсчета
полученных на предыдущем шаге для фиксированного номера спектрального отсчета  :
: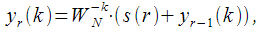
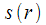 – отсчет входного сигнала с номером
– отсчет входного сигнала с номером  . Данное рекуррентное соотношение на шаге с номером
. Данное рекуррентное соотношение на шаге с номером  приводит нас к
приводит нас к 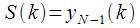 , т.е. Об этом говорит сайт https://intellect.icu . на
, т.е. Об этом говорит сайт https://intellect.icu . на 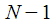 -ом шаге мы получим спектральный отсчет с номером
-ом шаге мы получим спектральный отсчет с номером  . Проанализировав (7), можно заметить, что рекуррентное соотношение можно трактовать как разностное уравнение БИХ-фильтра с комплексным коэффициентом
. Проанализировав (7), можно заметить, что рекуррентное соотношение можно трактовать как разностное уравнение БИХ-фильтра с комплексным коэффициентом 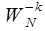 , структурная схема которого приведена на рисунке 1 .
, структурная схема которого приведена на рисунке 1 .
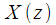 и
и 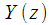 z – образы
z – образы 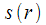 и
и 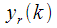 соответственно, выражение (7) можно представить в виде:
соответственно, выражение (7) можно представить в виде: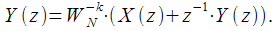

 и преобразовали выражение ДПФ для одного фиксированного спектрального отсчета к рекуррентному соотношению, которое позволяет нам на
и преобразовали выражение ДПФ для одного фиксированного спектрального отсчета к рекуррентному соотношению, которое позволяет нам на 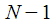 -м шаге получить значение искомого
-м шаге получить значение искомого  -го спектрального отсчета
-го спектрального отсчета 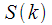 . При этом все промежуточные значения рекуррентного соотношения
. При этом все промежуточные значения рекуррентного соотношения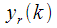 нас не интересуют, а интересует только
нас не интересуют, а интересует только 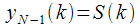 . Это важно и пригодится нам в дальнейшем. После мы рекуррентное соотношение трактовали как разностное уравнение БИХ фильтра с передаточной характеристикой (9). В результате мы получили «хитроумный фильтр» с комплексным коэффициентом
. Это важно и пригодится нам в дальнейшем. После мы рекуррентное соотношение трактовали как разностное уравнение БИХ фильтра с передаточной характеристикой (9). В результате мы получили «хитроумный фильтр» с комплексным коэффициентом 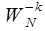 применение которого на
применение которого на 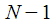 -ой итерации на выходе дает
-ой итерации на выходе дает 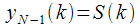 . При фиксированном
. При фиксированном  значение комплексного коэффициента
значение комплексного коэффициента 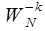 всегда постоянно.
всегда постоянно.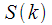 при использовании БИХ — фильтра требуется
при использовании БИХ — фильтра требуется 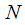 комплексных умножений и сложений, что не дает никаких преимуществ по сравнению с вычислением ДПФ «в лоб» согласно выражению (1).
комплексных умножений и сложений, что не дает никаких преимуществ по сравнению с вычислением ДПФ «в лоб» согласно выражению (1). :
: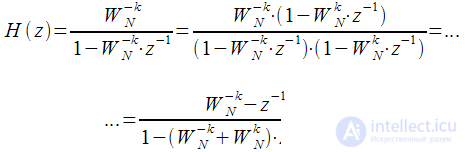
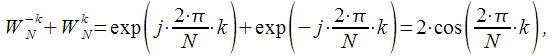
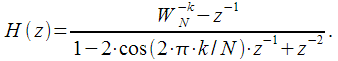
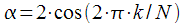 .
.
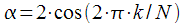 – вещественный коэффициент, соответственно умножения в рекурсивной ветви фильтра стали вещественными, причем умножения на -1 можно не учитывать. У нас остался один комплексный коэффициент
– вещественный коэффициент, соответственно умножения в рекурсивной ветви фильтра стали вещественными, причем умножения на -1 можно не учитывать. У нас остался один комплексный коэффициент 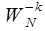 в числителе передаточной характеристики. Но мы выяснили, что промежуточные значения
в числителе передаточной характеристики. Но мы выяснили, что промежуточные значения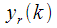 нам не важны, соответственно умножать на
нам не важны, соответственно умножать на 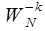 можно только на
можно только на 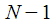 итерации, когда рассчитывается непосредственно
итерации, когда рассчитывается непосредственно 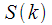 , поскольку на промежуточные значения
, поскольку на промежуточные значения 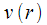 это никак не повлияет. Таким образом применение фильтра второго порядка позволяет рассчитать
это никак не повлияет. Таким образом применение фильтра второго порядка позволяет рассчитать 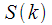 для фиксированного
для фиксированного  с использованием
с использованием 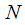 умножений, но не комплексных, а вещественных, что приводит к сокращению вычислений в 2 раза (одно комплексное умножение требует два вещественных), плюс одно комплексное умножение на
умножений, но не комплексных, а вещественных, что приводит к сокращению вычислений в 2 раза (одно комплексное умножение требует два вещественных), плюс одно комплексное умножение на 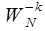 на последней итерации при расчете непосредственно
на последней итерации при расчете непосредственно 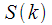 .
.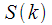 равен:
равен: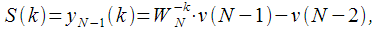
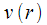 – промежуточные значения (смотри рисунок 2), которые рассчитываются итерационно:
– промежуточные значения (смотри рисунок 2), которые рассчитываются итерационно: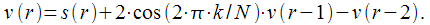
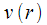 согласно (14), после чего последние два значения
согласно (14), после чего последние два значения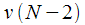 и
и 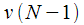 используются для расчета спектрального отсчета
используются для расчета спектрального отсчета 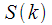 .
.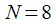 , исходный сигнал
, исходный сигнал 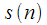 показан на рисунке 3.
показан на рисунке 3.
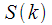 с номером
с номером 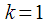 . Предварительно рассчитаем коэффициент
. Предварительно рассчитаем коэффициент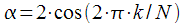 и
и 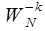 :
: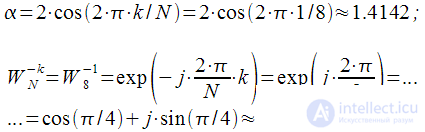
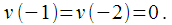
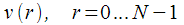 согласно (14):
согласно (14):
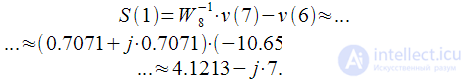
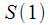 полностью соответствует результату ДПФ.
полностью соответствует результату ДПФ.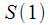 согласно рассмотренному примеру.
согласно рассмотренному примеру. . Для реализации расчета всех
. Для реализации расчета всех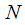 спектральных отсчетов, необходимо параллельно поставить
спектральных отсчетов, необходимо параллельно поставить 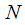 таких фильтров. Преимущество алгоритма Герцеля заключается в том, что каждый спектральный отсчет рассчитывается независимо от других, и не нужно считать все ДПФ ради нескольких отсчетов. Это широко применяется при декодировании DTMF сигналов когда анализируется амплитуда нескольких гармоник сигнала. Но алгоритм Герцеля также обладает недостатком. Для расчета одного спектрального отсчета требуется
таких фильтров. Преимущество алгоритма Герцеля заключается в том, что каждый спектральный отсчет рассчитывается независимо от других, и не нужно считать все ДПФ ради нескольких отсчетов. Это широко применяется при декодировании DTMF сигналов когда анализируется амплитуда нескольких гармоник сигнала. Но алгоритм Герцеля также обладает недостатком. Для расчета одного спектрального отсчета требуется 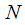 итераций, причем промежуточные значения
итераций, причем промежуточные значения 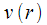 , кроме двух последних, не несут полезной информации, но их приходится рассчитывать. Алгоритм Герцеля малопривлекателен для расчета всех спектральных отсчетов ДПФ ввиду высокой вычислительной сложности. Для расчета «полного» ДПФ гораздо лучше подходят алгоритмы быстрого преобразования Фурье.
, кроме двух последних, не несут полезной информации, но их приходится рассчитывать. Алгоритм Герцеля малопривлекателен для расчета всех спектральных отсчетов ДПФ ввиду высокой вычислительной сложности. Для расчета «полного» ДПФ гораздо лучше подходят алгоритмы быстрого преобразования Фурье.
Комментарии
Оставить комментарий
Цифровая обработка сигналов
Термины: Цифровая обработка сигналов