Лекция
Привет, Вы узнаете о том , что такое свёртка ма тический анализ , Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое свёртка ма тический анализ , настоятельно рекомендую прочитать все из категории Цифровая обработка сигналов.
Свертка фу́нкций — операция в функциональном анализе.
По определению, свертка — это математическая операция, примененная к двум функциям f и g, порождающая третью функцию, которая иногда может рассматриваться как модифицированная версия одной из первоначальных. По существу, это особый вид интегрального преобразования.
Понятие свертки обобщается для функций, определенных на группах, а также мер.
Операцию свертки можно интерпретировать как «схожесть» одной функции с отраженной и сдвинутой копией другой.
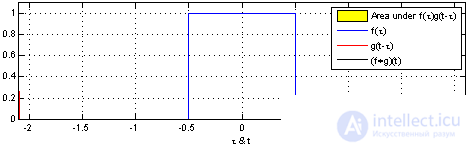
Свертка двух прямоугольных импульсов: в результате дает треугольный импульс.
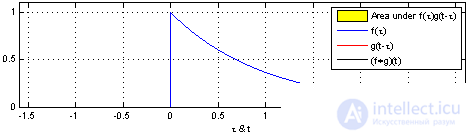
Свертка прямоугольного импульса (входного сигнала) с импульсным откликом RC цепи
Свертка функций – это важнейшее математическое понятие, которое используется почти во всех областях науки и техники, в том числе, оно широко применяется для оценки систем изображения и для процессинга цифровых изображений. Свертка двух функций – это математическая операция двух функций h(x) и f(x), порождающая третью функцию g(x), которая может рассматриваться как модифицированная версия одной из первоначальных, например, после операций осреднения или сглаживания. Свертка h(x) и f(x) записывается как h∗f (символ звездочки). Для непрерывных функций она определяется как интеграл от произведения двух функций после того, как одна реверсируется и смещается. По существу, это особый вид интегрального преобразования: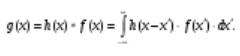 
(5.9)
Операция свертки иллюстрируется на рис. 5.8 для двух функций, заданных в виде прямоугольных импульсов разной длительности.
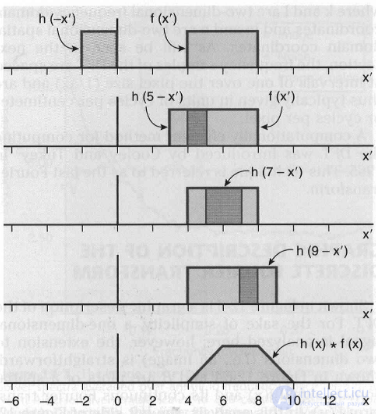
Рис. 5.8. Пример свертки двух непрерывных функций h(x) и f(x). Более темным цветом показана площадь, равная интегралу (5.9) при разных значениях x (адаптировано из [4])
Одномерная дискретная свертка двух дискретных функций h(i) и f(i) длиной N определяется как
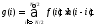(5.10)
С точки зрения вычислительного процесса более легким и быстрым способом расчета свертки двух функций является использование теоремы свертки. В этой теореме доказывается, что свертка двух функций эквивалентна перемножению их преобразований Фурье в частотном пространстве. Таким образом, уравнение свертки (5.9) можно выразить в виде
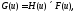(5.11)
где H(u) и F(u) – преобразование Фурье функций h(x) и f(x) в частотном пространстве.
Пусть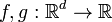 
— две функции, интегрируемые относительно меры Лебега на пространстве 
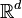. Об этом говорит сайт https://intellect.icu . Тогда их сверткой называется функция 
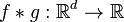, определенная формулой
 |
 |
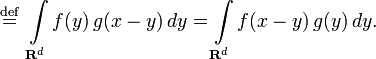В частности, при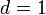 
формула принимает вид:
|
 |
Свертка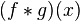 
определена при почти всех 
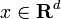и интегрируема.
Впервые интегралы, представляющие собой свертку двух функций, встречаются в трудах Леонарда Эйлера (1760-е годы); позднее свертка появляется у Лапласа,Лакруа, Фурье, Коши, Пуассона и других математиков. Обозначение свертки функций при помощи звездочки впервые предложил Вито Вольтерра в 1912 году на своих лекциях в Сорбонне (опубликованы годом позже)[1].
.
.
.
,
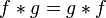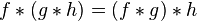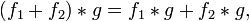
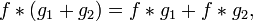
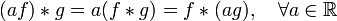где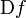 
обозначает производную функции 
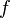по любой переменной.
,
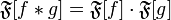где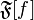 
обозначает преобразование Фурье функции .
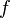Пусть 
— группа Ли, оснащенная мерой Хаара 
, и 
— две функции, определенные на . Тогда их сверткой называется функция
.
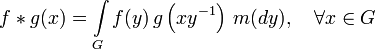Пусть есть борелевское пространство 
и две меры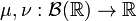 
. Тогда их сверткой называется мера
,
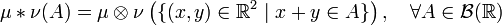где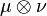 
обозначает произведение мер 
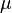и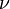 
.
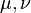абсолютно непрерывны относительно меры Лебега . Обозначим их производные Радона — Никодима:
.
Тогда 
также абсолютно непрерывна относительно , и ее производная Радона — Никодима 
имеет вид
.
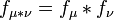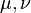— вероятностные меры, то также является вероятностной мерой.Если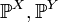 
— распределения двух независимых случайных величин 
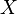и 
, то
,
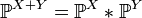где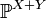 
— распределение суммы 
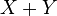. В частности, если 
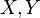абсолютно непрерывны и имеют плотности 
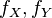, то случайная величина 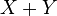также абсолютно непрерывна и ее плотность имеет вид:
.
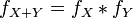В заключение, эта статья об свёртка ма тический анализ подчеркивает важность того что вы тут, расширяете ваше сознание, знания, навыки и умения. Надеюсь, что теперь ты понял что такое свёртка ма тический анализ и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровая обработка сигналов
Из статьи мы узнали кратко, но содержательно про свёртка ма тический анализ
Комментарии
Оставить комментарий
Цифровая обработка сигналов
Термины: Цифровая обработка сигналов