Привет, сегодня поговорим про оконные функции, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое
оконные функции, цифровой спектральный анализ , настоятельно рекомендую прочитать все из категории Цифровая обработка сигналов.
Введение
В данной статье приведем пример использования оконных функций при цифровом спектральном анализе. Для этого мы смоделируем несколько сигналов и проанализируем их спектр вычисленный без оконного сглаживания и при использовании некоторых окон.
Пример использования различных оконных функций для спектрального анализа конечного сигнала
Рассмотрим первый пример. Пусть сигнал состоит из трех гармоник:
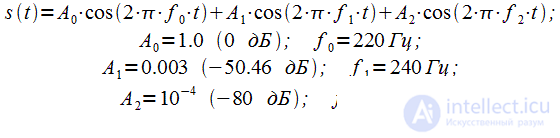 |
(1) |
Динамический диапазон данного сигнала, который можно определить как отношение максимальной амплитуды гармоники к минимальной составляет 80 дБ. Частоту дискретизации выберем равной
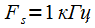
, выборка равна
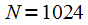
отсчетам сигнала. Расстояние между спектральными отсчетами:
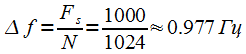 |
(2) |
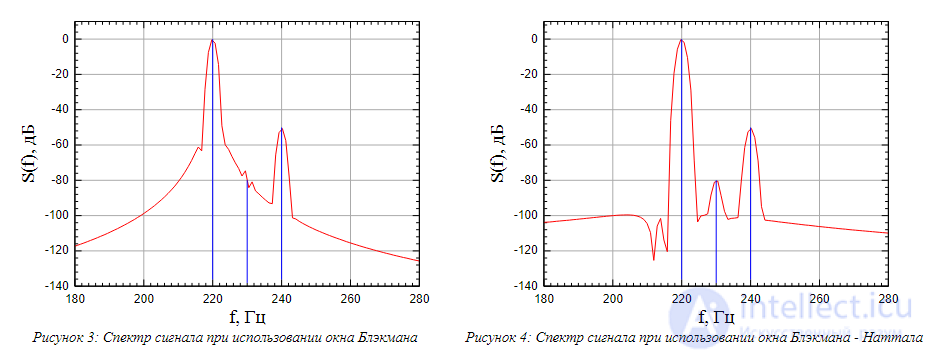
Рассчитаем спектр данного сигнала при использовании прямоугольного окна, окна Хеммигна, окна Блэкмана и окна Блэкмана-Наттала. На рисунках 1-4 представлены результаты спектрального анализа при использовании различных окон. Синим цветом показаны истинные гармоники сигнала (1).
|
Рисунок 1: Спектр сигнала при использовании прямоугольного окна (без сглаживания)
|
Рисунок 2: Спектр сигнала при использовании окна Хемминга
|
|
Рисунок 3: Спектр сигнала при использовании окна Блэкмана
|
Рисунок 4: Спектр сигнала при использовании окна Блэкмана - Наттала
|
Проанализируем приведенные результаты. Без оконного сглаживания, ввиду очень высокого уровня боковых лепестков спектра прямоугольного окна (-13 дБ) в спектре обнаруживается только гармоника на частоте 220 Гц. Остальные гармоники на частотах 230 Гц и 240 Гц скрыты боковыми лепестками спектра прямоугольного окна. При использовании окна Хемминга уровень боковых лепестков которого составляет -42 дБ, мы хорошо видим гармонику на частоте 220 Гц, и также слабозаметные составляющие на частоте 240 Гц. Сигнал на частоте 240 Гц по уровню ниже боковых лепестков спектра окна Хемминга, поэтому он заметен очень слабо. Уровень боковых лепестков окна Блэкмана (-58 дБ) ниже чем амплитуда гармоники на частоте 240 Гц (-50.46 дБ), поэтому использование окна Блэкмана позволят обнаружить составляющие на частотах 220 Гц и 240 Гц. Однако уровень боковых лепестков окна Блэкмана выше, чем амплитуда сигнала на частоте 230 Гц (-80 дБ), поэтому применение окна Блэкмана не позволяет обнаружить сигнал на частоте 230 Гц. Об этом говорит сайт https://intellect.icu . Ну и наконец, окно Блэкмана — Наттала, спектр которого имеет уровень боковых лепестков -98 дБ позволяет обнаружить все спектральные составляющие.
Правило выбора оконной функции для обеспечения динамического диапазона спектрального анализа
Можно сформулировать правило. При спектральном анализе сигнала с известным или заданным динамическим диапазоном необходимо выбирать такую оконную функцию, уровень боковых лепестков спектра которой меньше заданного динамического диапазона. В противном случае некоторые спектральные составляющие сигнала могут быть не обнаружены. Так например если динамический диапазон сигнала не превышает 40 дБ целесообразно использовать окно Хемминга, боковые лепестки спектра которой не превышают -42 дБ. Если же динамический диапазон сигнала не превышает 60 дБ, то можно использовать окно Блэкмана (уровень боковых лепестков спектра -58 дБ).
Если динамический диапазон сигнала не известен, то можно его оценить исходя из разрядности АЦП по формуле:
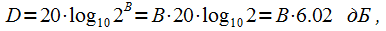 |
(3) |
где
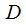
-динамический диапазон в децибелах,
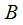
- количество разрядов АЦП. В случае 8-битного АЦП динамический диапазон сигнала можно считать равным 48.16 дБ, а в случае 16 -битного 96.32 дБ. Также можно априори оценить динамический диапазон исходя из типа обрабатываемого сигнала. Например динамический диапазон аудиосигнала не превышает 40 дБ и при спектральном анализе аудиосигналов можно использовать окно Хемминга даже при 16-битном квантовании.
В приведенном примере гармоники сигнала отстоят друг от друга на 10 Гц. При этом использование оконного сглаживания приводит к ухудшению разрешения по частоте ввиду расширения главного лепестка спектра оконной функции (это подробно описано здесь). В нашем случае ширина главного лепестка спектра окна Блэкмана — Наттала составляет
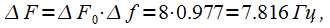 |
(4) |
где
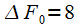
- нормированная ширина главного лепестка спектра окна Блэкмана — Наттала по нулевому уровню (безразмерная величина), взятая из таблицы свойств оконных функций. В данном случае важно, что
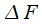
меньше, чем расстояние между частотами спектральных составляющих сигнала (10 Гц). Таким образом применение оконных функций ухудшает разрешающую способность спектрального анализа. Если задано разрешение по частоте

при котором требуется проанализировать спектр сигнала, то необходимо выполнить условие

или
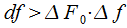 . . |
(5) |
С учетом (2)
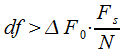 |
(6) |
Правило выбора оконной функции для обеспечения разрешения по частоте
При заданном окне, которое выбирается исходя из динамического диапазона сигнала,
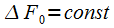
для обеспечения требуемого разрешения по частоте необходимо выполнение условия (6). При фиксированной частоте дискретизации
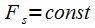
для увеличения разрешения по частоте необходимо увеличивать длину выборки
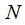
. Например необходимо обеспечить разрешение по частоте

частота дискретизации
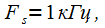
сглаживание осуществляется при использовании окна Блэкмана — Наттала
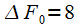
. Тогда из (6) получаем:
 |
(7) |
Т.е. размер выборки БПФ должен составлять 4096 точек.
Рассмотрим второй пример. Пусть сигнал состоит из трех гармоник:
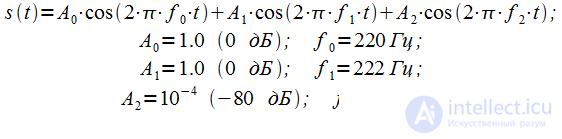 |
(8) |
Динамический диапазон сигнала составляет 80 дБ, поэтому необходимо использовать окно Блэкмана-Наттала. Частоту дискретизации зададим равной
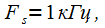
требуемое разрешение по частоте
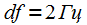
, так как нулевая и первая гармоники сигнала (8) отстоят на
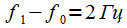
. Согласно (7) размер выборки БПФ должен составлять
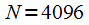
точек. На рисунках 5 и 6 показаны спектры сигнала при использовании окна Блэкмана — Наттала и различном размере выборки БПФ. Синим цветом показаны истинные гармоники сигнала (8).
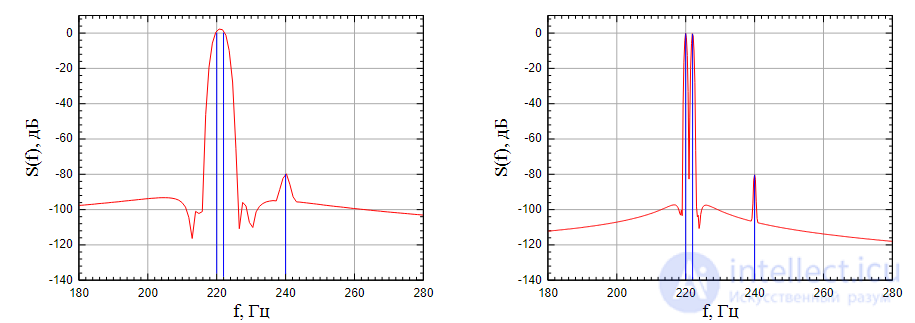
Рисунок 5: Спектр сигнала при использовании окна Блэкмана — Наттала, 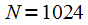 |
Рисунок 6: Спектр сигнала при использовании окна Блэкмана — Наттала, 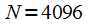 |
Сравнив рисунки 5 и 6 можно заметить, что окно удовлетворяет динамическому диапазону сигнала и гармоника на частоте 240 Гц обнаруживается на обоих спектрах. Однако при
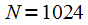
разрешение по частоте не позволяет разделить гармоники на частотах 220 и 222 Гц, поскольку не выполняется условие (6). При
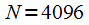
условие (6) выполняется и все три гармоники различимы в спектре (рисунок 6).
Выводы
Итак подведем итог.
Для качественного спектрального анализа необходимо:
1. Правильно выбрать оконную функцию исходя из динамического диапазона сигнала, так чтобы уровень боковых лепестков спектра оконной функции был меньше динамического диапазона сигнала.
2. Выбрать размер выборки БПФ для обеспечения требуемого разрешения по частоте согласно (6) исходя из частоты дискретизации и свойств выбранной оконной функции.
Таким образом, в статье приведены примеры спектрального анализа сигналов с использование оконных функций, а также даны практические рекомендации по выбору оконных функций и размера выборки БПФ.
Надеюсь, эта статья про оконные функции, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое оконные функции, цифровой спектральный анализ
и для чего все это нужно, а если не понял, или есть замечания,
то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Цифровая обработка сигналов
Из статьи мы узнали кратко, но содержательно про оконные функции
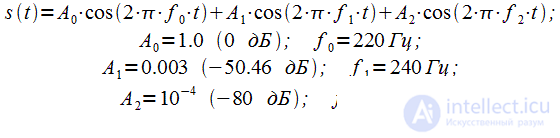
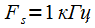 , выборка равна
, выборка равна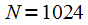 отсчетам сигнала. Расстояние между спектральными отсчетами:
отсчетам сигнала. Расстояние между спектральными отсчетами: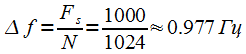


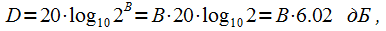
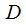 -динамический диапазон в децибелах,
-динамический диапазон в децибелах, 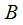 - количество разрядов АЦП. В случае 8-битного АЦП динамический диапазон сигнала можно считать равным 48.16 дБ, а в случае 16 -битного 96.32 дБ. Также можно априори оценить динамический диапазон исходя из типа обрабатываемого сигнала. Например динамический диапазон аудиосигнала не превышает 40 дБ и при спектральном анализе аудиосигналов можно использовать окно Хемминга даже при 16-битном квантовании.
- количество разрядов АЦП. В случае 8-битного АЦП динамический диапазон сигнала можно считать равным 48.16 дБ, а в случае 16 -битного 96.32 дБ. Также можно априори оценить динамический диапазон исходя из типа обрабатываемого сигнала. Например динамический диапазон аудиосигнала не превышает 40 дБ и при спектральном анализе аудиосигналов можно использовать окно Хемминга даже при 16-битном квантовании.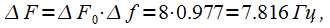
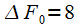 - нормированная ширина главного лепестка спектра окна Блэкмана — Наттала по нулевому уровню (безразмерная величина), взятая из таблицы свойств оконных функций. В данном случае важно, что
- нормированная ширина главного лепестка спектра окна Блэкмана — Наттала по нулевому уровню (безразмерная величина), взятая из таблицы свойств оконных функций. В данном случае важно, что 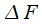 меньше, чем расстояние между частотами спектральных составляющих сигнала (10 Гц). Таким образом применение оконных функций ухудшает разрешающую способность спектрального анализа. Если задано разрешение по частоте
меньше, чем расстояние между частотами спектральных составляющих сигнала (10 Гц). Таким образом применение оконных функций ухудшает разрешающую способность спектрального анализа. Если задано разрешение по частоте  при котором требуется проанализировать спектр сигнала, то необходимо выполнить условие
при котором требуется проанализировать спектр сигнала, то необходимо выполнить условие  или
или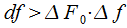 .
.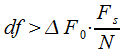
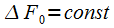 для обеспечения требуемого разрешения по частоте необходимо выполнение условия (6). При фиксированной частоте дискретизации
для обеспечения требуемого разрешения по частоте необходимо выполнение условия (6). При фиксированной частоте дискретизации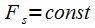 для увеличения разрешения по частоте необходимо увеличивать длину выборки
для увеличения разрешения по частоте необходимо увеличивать длину выборки 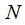 . Например необходимо обеспечить разрешение по частоте
. Например необходимо обеспечить разрешение по частоте  частота дискретизации
частота дискретизации 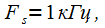 сглаживание осуществляется при использовании окна Блэкмана — Наттала
сглаживание осуществляется при использовании окна Блэкмана — Наттала 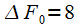 . Тогда из (6) получаем:
. Тогда из (6) получаем:
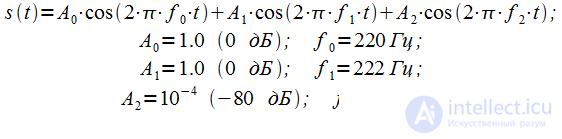
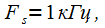 требуемое разрешение по частоте
требуемое разрешение по частоте 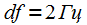 , так как нулевая и первая гармоники сигнала (8) отстоят на
, так как нулевая и первая гармоники сигнала (8) отстоят на 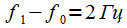 . Согласно (7) размер выборки БПФ должен составлять
. Согласно (7) размер выборки БПФ должен составлять 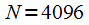 точек. На рисунках 5 и 6 показаны спектры сигнала при использовании окна Блэкмана — Наттала и различном размере выборки БПФ. Синим цветом показаны истинные гармоники сигнала (8).
точек. На рисунках 5 и 6 показаны спектры сигнала при использовании окна Блэкмана — Наттала и различном размере выборки БПФ. Синим цветом показаны истинные гармоники сигнала (8).
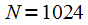
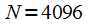
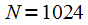 разрешение по частоте не позволяет разделить гармоники на частотах 220 и 222 Гц, поскольку не выполняется условие (6). При
разрешение по частоте не позволяет разделить гармоники на частотах 220 и 222 Гц, поскольку не выполняется условие (6). При 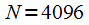 условие (6) выполняется и все три гармоники различимы в спектре (рисунок 6).
условие (6) выполняется и все три гармоники различимы в спектре (рисунок 6).
Комментарии
Оставить комментарий
Цифровая обработка сигналов
Термины: Цифровая обработка сигналов