Лекция
Привет, сегодня поговорим про фильтры фарроу, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое фильтры фарроу, farrow filters , фильтр третьего порядка, ресэмплинг, resampling , настоятельно рекомендую прочитать все из категории Цифровая обработка сигналов.
Для изменения частоты дискретизации, или для сдвига дискретного сигнала по фазе на величину меньшую интервала дискретизации, необходимо представить дискретный сигнал в виде непрерывной функции времени и произвести его повторную дискретизацию (resampling) или как еще говорят передискретизацию.
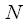 отсчетов дискретного сигнала
отсчетов дискретного сигнала 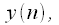
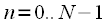 . Необходимо произвести
ресэмплинг и получить
. Необходимо произвести
ресэмплинг и получить 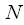 отсчетов дискретного сигнала
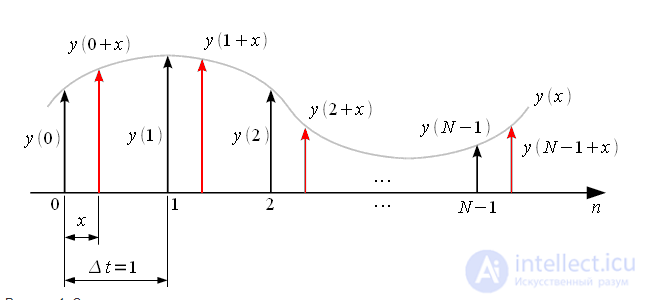
отсчетов дискретного сигнала 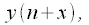 как это показано на рисунке 1. Интервал дискретизации
как это показано на рисунке 1. Интервал дискретизации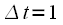 . Черным показан исходный сигнал, красным - результат ресэмплинга.
. Черным показан исходный сигнал, красным - результат ресэмплинга.
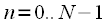 произвести интерполяцию, т.е. восстановление непрерывного сигнала
произвести интерполяцию, т.е. восстановление непрерывного сигнала 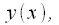 затем рассчитать его дискретные значения для каждого нового
затем рассчитать его дискретные значения для каждого нового 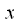 . Осуществлять интерполяцию можно различными способами, в данной статье речь пойдет о полиномиальной интерполяции.
. Осуществлять интерполяцию можно различными способами, в данной статье речь пойдет о полиномиальной интерполяции.
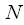 точек проходит полином
точек проходит полином 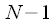 степени
степени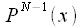 и при том только один. Например через две точки можно провести только одну прямую, через три точки только одну параболу и так далее. Соответственно через
и при том только один. Например через две точки можно провести только одну прямую, через три точки только одну параболу и так далее. Соответственно через 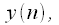
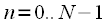 также можно провести единственный полином степени
также можно провести единственный полином степени 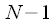 , который будет являться результатом интерполяции, то есть:
, который будет являться результатом интерполяции, то есть: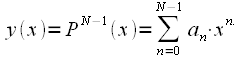 или или 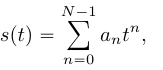 |
(1) |
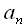 - коэффициенты полинома, которые необходимо рассчитать на основе отсчетов сигнала
- коэффициенты полинома, которые необходимо рассчитать на основе отсчетов сигнала  Тогда подставляя нужные значения
Тогда подставляя нужные значения 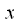 можно произвести ресэмплинг.
можно произвести ресэмплинг.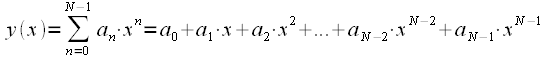 |
(2) |
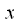 за скобки:
за скобки: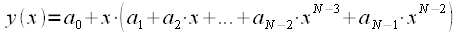 |
(3) |
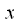 за скобки:
за скобки: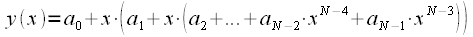 |
(4) |
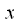 за скобки, получим множество вложенных скобок:
за скобки, получим множество вложенных скобок: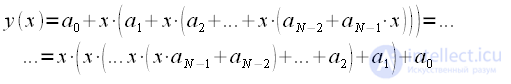 |
(5) |
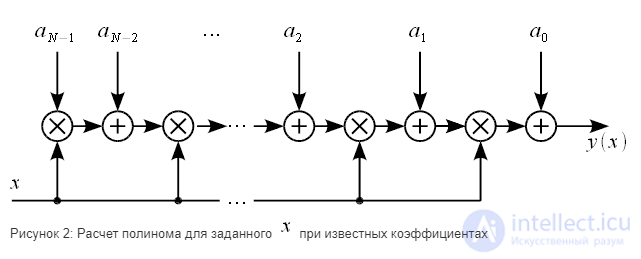
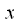 при известных коэффициентах
при известных коэффициентах
 потом прибавляется
потом прибавляется 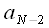 получается «самые внутренние скобки» выражения (5)
получается «самые внутренние скобки» выражения (5)  . «самые внутренние скобки» умножаются на
. «самые внутренние скобки» умножаются на 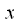 и так далее собираются все скобки и получается
и так далее собираются все скобки и получается 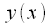 .
.
 . Получим кубический полином:
. Получим кубический полином: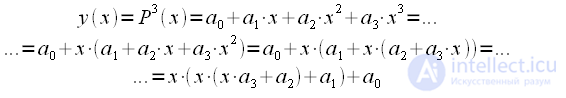 |
(6) |
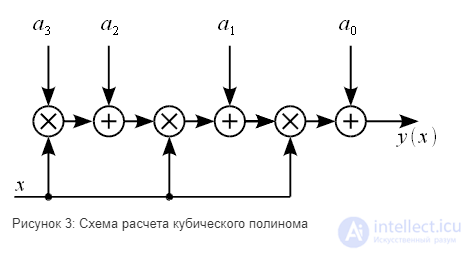
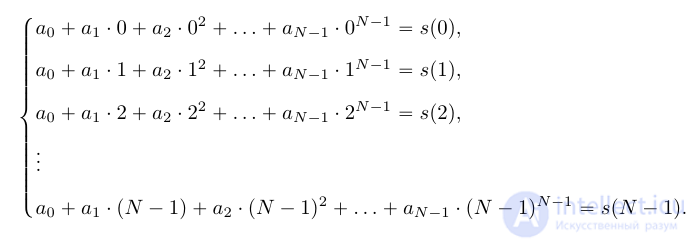
Данная система может быть записана в матричной форме как:
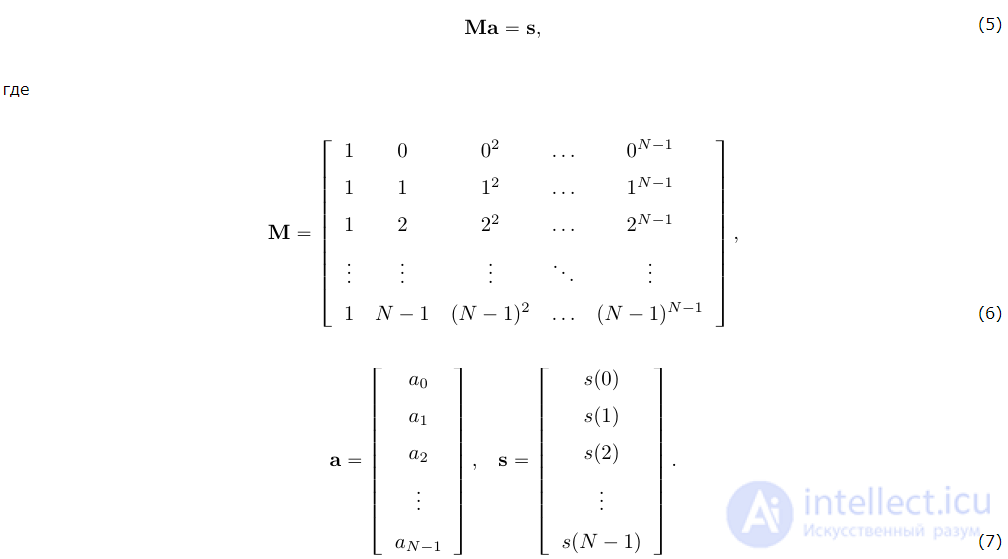
Решение системы уравнений может быть получено в виде:
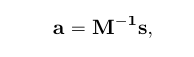 (8*)
(8*)
где M — обратная матрица для матрицы M-1 .
Для решения задачи передискретизации необходимо по имеющемуся дискретному сигналу 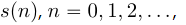 , произвести восстановление непрерывного сигнала
, произвести восстановление непрерывного сигнала 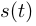 и рассчитать его дискретные значения для моментов времени
и рассчитать его дискретные значения для моментов времени  , где
, где 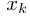 рассчитывается согласно (2).
рассчитывается согласно (2).
Процесс передискретизации для частного случая 2 (компенсация дробной задержки) показан на рисунке 2.
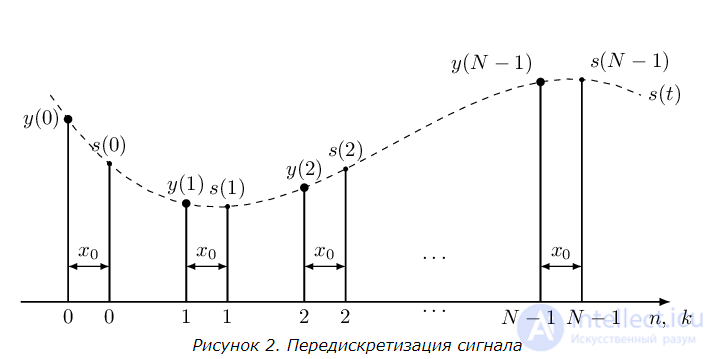
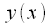 на основе дискретных отсчетов
на основе дискретных отсчетов 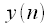 . Для этого можно составить систему линейных уравнений:
. Для этого можно составить систему линейных уравнений:
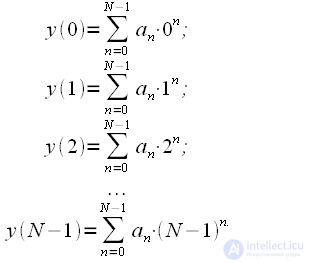 |
(7) |
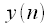 . Об этом говорит сайт https://intellect.icu . Кроме того для решения системы уравнений требуется обращение матрицы, что невозможно обеспечить в реальном времени, так как для обращении матрицы требуется
. Об этом говорит сайт https://intellect.icu . Кроме того для решения системы уравнений требуется обращение матрицы, что невозможно обеспечить в реальном времени, так как для обращении матрицы требуется 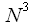 операций умножения. Таким образом для построения кубического полинома при
операций умножения. Таким образом для построения кубического полинома при 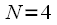 требуется 64 умножения! Разумеется подобный подход не может быть применен на практике. Далее будет рассмотрен фильтр Фарроу (Farrow filter) построения кубического полинома при использовании всего трех умножений.
требуется 64 умножения! Разумеется подобный подход не может быть применен на практике. Далее будет рассмотрен фильтр Фарроу (Farrow filter) построения кубического полинома при использовании всего трех умножений.
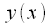 может быть представлен как сумма произведения своих отсчетов
может быть представлен как сумма произведения своих отсчетов 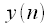 на соответствующий полином Лагранжа
на соответствующий полином Лагранжа :
: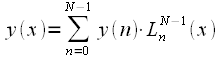 |
(8) |
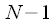 , равный единице при
, равный единице при 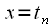 , где
, где 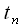 - момент дискретизации
- момент дискретизации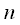 - го отсчета и равный нулю в другие моменты дискретизации.
- го отсчета и равный нулю в другие моменты дискретизации.Полином третьей степени может быть построен по четырем точкам согласно выражению (8*).
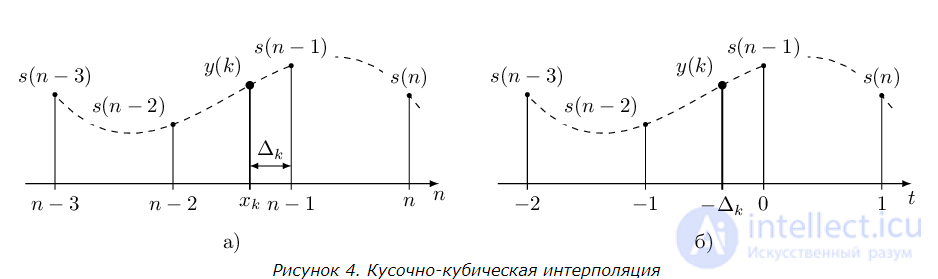
Для любого 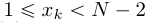 можно получить два отсчета правее и левее xk как это показано на рисунке 4a. Тогда значение y(k) может быть рассчитано на основе четырех входных отсчетов
можно получить два отсчета правее и левее xk как это показано на рисунке 4a. Тогда значение y(k) может быть рассчитано на основе четырех входных отсчетов 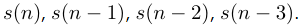
Обратим внимание, что матрица M зависит только от индексов входных отсчетов сигнала. Значит, чтобы не пересчитывать матрицу M и обратную M-1 для каждого нового k, мы можем зафиксировать индексы по оси абсцисс. Пусть 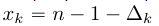 (cм. рисунок 4а), тогда вместо xk мы будем использовать значение
(cм. рисунок 4а), тогда вместо xk мы будем использовать значение 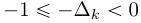 , как это показано на рисунке 4б. В этом случае мы можем один раз расчитать обратную матрицу
, как это показано на рисунке 4б. В этом случае мы можем один раз расчитать обратную матрицу 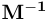 и использовать ее для любого
и использовать ее для любого 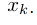 .
.
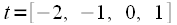 . Каждый из полиномов равен единице в одном из моментов дискретизации и равен нулю в остальных (это отмечено маркерами).
. Каждый из полиномов равен единице в одном из моментов дискретизации и равен нулю в остальных (это отмечено маркерами).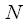 отсчетов сигнала используется
отсчетов сигнала используется 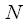 разных полиномов. Каждый полином Лагранжа может быть записан в виде:
разных полиномов. Каждый полином Лагранжа может быть записан в виде:|
|
(9) |
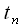 и
и  моменты дискретизации.
моменты дискретизации.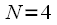 и моментов дискретизации
и моментов дискретизации 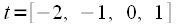 :
: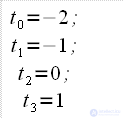 |
(10) |
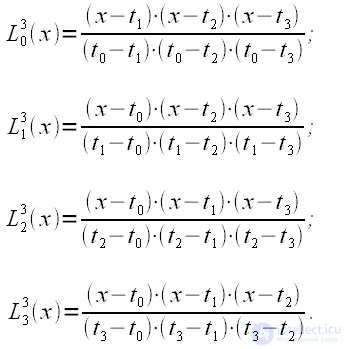 |
(11) |
 |
(12) |
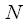 .
.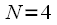 с использованием кубических полиномов Лагранжа (12). При
с использованием кубических полиномов Лагранжа (12). При 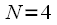 выражение (8):
выражение (8):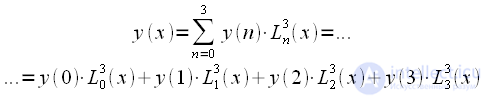 |
(13) |
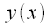 в выражении (13) есть сумма кубических полиномов, а значит
в выражении (13) есть сумма кубических полиномов, а значит 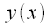 также кубический полином с коэффициентами
также кубический полином с коэффициентами 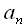 ,
, 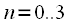 .
. |
(14) |
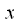 , получим кубический полином:
, получим кубический полином: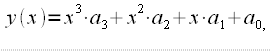 |
(15) |
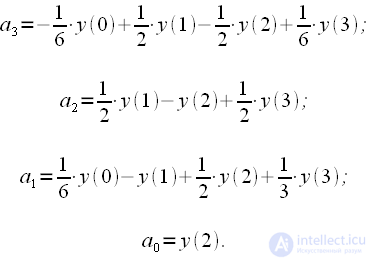 |
(16) |
 зависят от четырех предыдущих значений. Таким образом коэффициенты полинома (15), в соответствии с формулой (16) можно получить используя КИХ-фильтры третьего порядка. На рисунке 5 показан пример расчета коэффициента полинома
зависят от четырех предыдущих значений. Таким образом коэффициенты полинома (15), в соответствии с формулой (16) можно получить используя КИХ-фильтры третьего порядка. На рисунке 5 показан пример расчета коэффициента полинома при помощи КИХ-фильтра.
при помощи КИХ-фильтра.
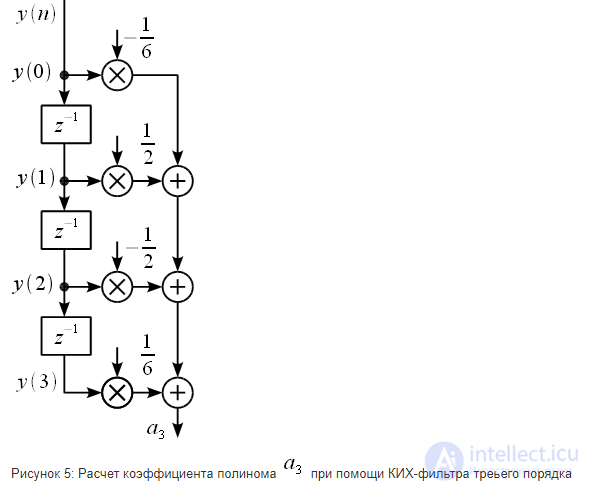
 при помощи КИХ-фильтра треьего порядка
при помощи КИХ-фильтра треьего порядка
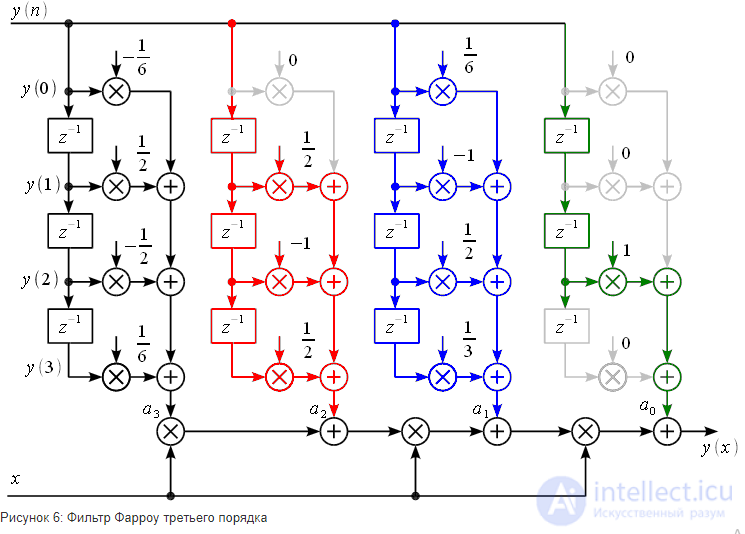
 – черным,
– черным, 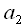 – красным
– красным 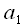 – синим,
– синим,  – зеленым. Серым обозначены ветви с умножением на ноль, которые можно выбросить из схемы. По схеме нетрудно посчитать, что для расчета всех коэффициентов полинома требуется 9 нетривиальных умножений (умножения на ноль и
– зеленым. Серым обозначены ветви с умножением на ноль, которые можно выбросить из схемы. По схеме нетрудно посчитать, что для расчета всех коэффициентов полинома требуется 9 нетривиальных умножений (умножения на ноль и 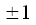 считаются тривиальными). Это уже не 64 как требуется для прямого решения системы уравнений, но еще и не три как было заявлено выше.
считаются тривиальными). Это уже не 64 как требуется для прямого решения системы уравнений, но еще и не три как было заявлено выше.
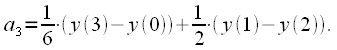 |
(17) |
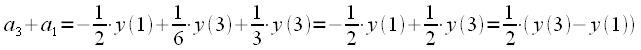 |
(18) |
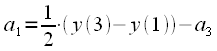 |
(19) |
 |
(20) |
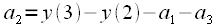 |
(21) |
 |
(22) |
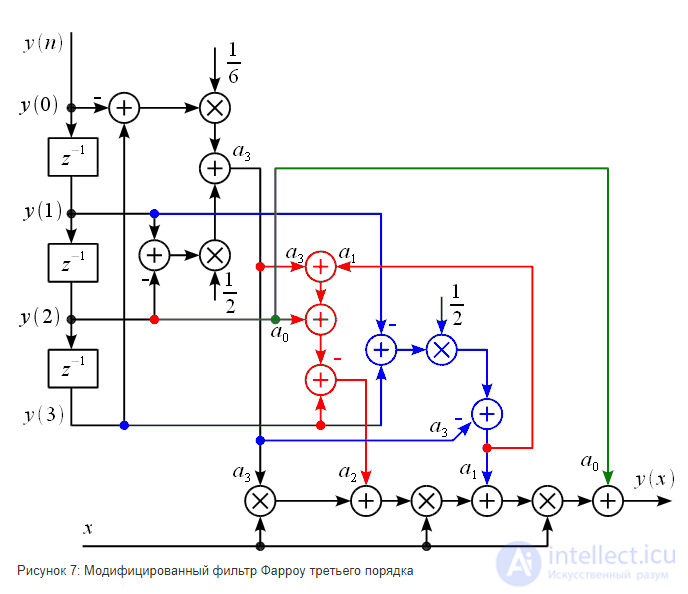
 (черные ветви), далее он используется для расчета коэффициента
(черные ветви), далее он используется для расчета коэффициента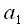 , синие ветви. Далее коэффициенты
, синие ветви. Далее коэффициенты  и
и 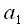 используются для расчета
используются для расчета 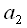 . Коэффициент
. Коэффициент 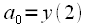 просто снимается после второй задержки.
просто снимается после второй задержки.
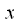 , которое требуется задавать для расчета
, которое требуется задавать для расчета 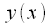 . Фильтр синтезировался исходя из следующих начальных данных: имеется 4 отсчета, взятые в моменты времени
. Фильтр синтезировался исходя из следующих начальных данных: имеется 4 отсчета, взятые в моменты времени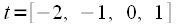 . Соответственно, для того чтобы получить значение полинома
. Соответственно, для того чтобы получить значение полинома 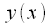 значение
значение  должно быть в интервале от -2 до 1, при этом
должно быть в интервале от -2 до 1, при этом  соответствует моменту дискретизации
соответствует моменту дискретизации 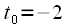 , а
, а 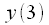 соответствует моменту дискретизации
соответствует моменту дискретизации  . Значение
. Значение  должно быть пересчитано в интервал от -2 до 1.
должно быть пересчитано в интервал от -2 до 1.
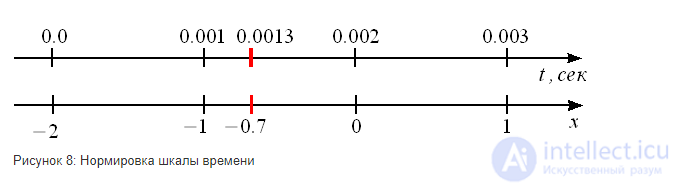
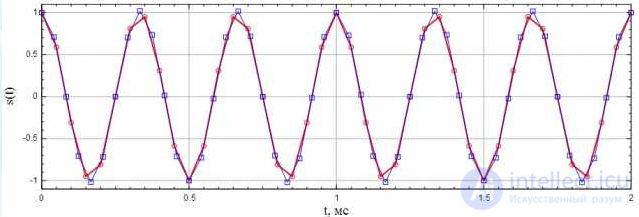
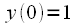 ,
,  ,
, 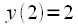 ,
, 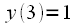 , взятые с частотой дискретизации 1 кГц, т.е.
, взятые с частотой дискретизации 1 кГц, т.е. 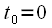 сек ,
сек , 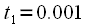 сек,
сек,  сек и
сек и 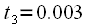 сек (рисунок 8). Рассчитать значение сигнала в момент времени
сек (рисунок 8). Рассчитать значение сигнала в момент времени 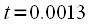 cек.
cек.
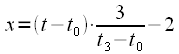 |
(23) |
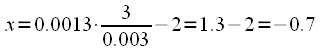 |
(24) |
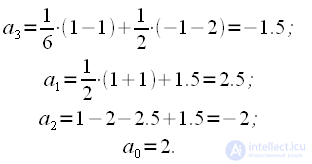 |
(25) |
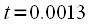 равно:
равно: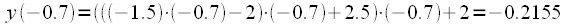 |
(26) |
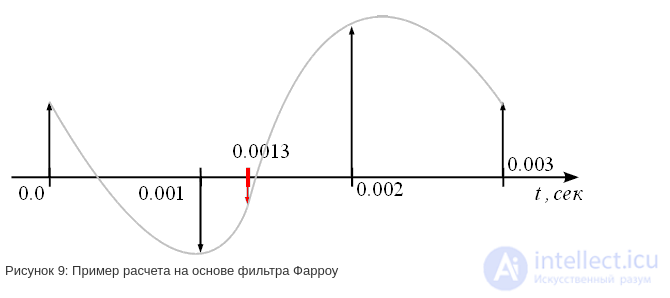
 Или
Или  . В предыдущем примере нельзя рассчитывать по данным четырем отсчетам значение сигнала например для
. В предыдущем примере нельзя рассчитывать по данным четырем отсчетам значение сигнала например для  , так как
, так как 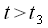 . Точнее рассчитать конечно можно, но значение не будет соответствовать действительности. С наибольшей точностью значения сигнала рассчитываются при нормированной
. Точнее рассчитать конечно можно, но значение не будет соответствовать действительности. С наибольшей точностью значения сигнала рассчитываются при нормированной  от -1 до 0. На практике необходимо стремиться вести пересчет шкалы времени именно в интервал от -1 до 0.
от -1 до 0. На практике необходимо стремиться вести пересчет шкалы времени именно в интервал от -1 до 0.
Надеюсь, эта статья про фильтры фарроу, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое фильтры фарроу, farrow filters , фильтр третьего порядка, ресэмплинг, resampling и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровая обработка сигналов
Комментарии
Оставить комментарий
Цифровая обработка сигналов
Термины: Цифровая обработка сигналов